Answers
Answer:
1) c
2)a
3)a
Step-by-step explanation:
Its write i rechecked it..
mark me the brainliest
thank u
hope it helped u
Related Questions
the length of a rectangle is four less than twice it’s width. If the width is 6 inches what is the length of the rectangle ?
Answers
Answer:
The question states four less than twice its width so we first find twice the width. The width is 6 and twice that is 12. Note that it says four less than, so four less than 12 is 8. so the length of the triangle is 8.
Step-by-step explanation:
Hope it helps! =D
Sheldon has scored 6/18 of the points in a basketball game. How can you use division to simplify the fraction of the points he scored? What is 6/18 in simplest form?
Answers
Answer:
1/3
Step-by-step explanation:
6/18, divide each side by 3 and you get 1/3
Para racionalizar el denominador de la fracción 6−2√3+5√
se requiere:
Answers
We need to multiply the numerator and denominator by 3-√5 to rationalize the denominator of the fraction. Therefore, the correct answer is option B
To rationalize the denominator of the fraction 6−2√3+√5, we need to eliminate any radicals present in the denominator. We can do this by multiplying both the numerator and denominator by an expression that will cancel out the radicals in the denominator.
In this case, we can observe that the denominator contains two terms with radicals: -2√3 and √5. To eliminate these radicals, we need to multiply both the numerator and denominator by an expression that contains the conjugate of the denominator.
The conjugate of the denominator is 6+2√3-√5, so we can multiply both the numerator and denominator by this expression, giving us:
(6−2√3+√5)(6+2√3-√5) / (6+2√3-√5)(6+2√3-√5)
Simplifying the numerator and denominator, we get:
(6 * 6) + (6 * 2√3) - (6 * √5) - (2√3 * 6) - (2√3 * 2√3) + (2√3 * √5) + (√5 * 6) - (√5 * 2√3) + (√5 * -√5) / ((6^2) - (2√3)^2 - (√5)^2)
This simplifies to:
24 + 3√3 - 7√5 / 20
Therefore, the correct answer is option B.
To learn more about numerator and denominator click on,
https://brainly.com/question/7067665
#SPJ1
Complete question is:
To rationalize the denominator of the fraction 6−2√3+√5
It is required:
A) multiply the denominator by 3−√5
B. multiply numerator and denominator by 3−√5
C. multiply numerator and denominator by 3+√5
D. multiply numerator and denominator by 6+√2
Pilots use precise decimal numbers to determine their altitude when flying. one airplane is flying at a height of 37,890.52 kilometers. another airplane flies at a height of 37,890.89 kilometers. which airplane has a higher altitude? explain how you know.
Answers
The second airplane, with a height of 37,890.89 kilometers, has a higher altitude than the first airplane, which is at 37,890.52 kilometers.
To determine which airplane has a higher altitude, we can compare the decimal parts of the altitudes provided.
The first airplane is flying at a height of 37,890.52 kilometers, and the second airplane is flying at a height of 37,890.89 kilometers. Comparing the decimal parts, we can see that 0.52 is smaller than 0.89.
In the decimal system, as the digits move to the right of the decimal point, their value decreases. So, when comparing two numbers with the same whole part (37,890 in this case), the one with a higher decimal part will be greater.
Therefore, the second airplane, with a height of 37,890.89 kilometers, has a higher altitude than the first airplane, which is at 37,890.52 kilometers.
Learn more about statistics here:
https://brainly.com/question/15525560
#SPJ8
Find the average value of the function f(x) = (x + 2) on the interval [0, 3].
![Find the average value of the function f(x) = (x + 2) on the interval [0, 3].](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/P5zl0SIYRlJ5Lz5JinzKHjLeHoS5AWmn.png)
Answers
The average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Calculate the definite integral of the function over the interval [a, b], then divide it by the interval's length (b - a), in order to determine the average value of a function f(x) over the interval.
Given that the interval is [0, 3] and the function f(x) = (x + 2), we have:
= (1/3) × [1/2 x² + 2x] evaluated from x=0 to x=3
= (1/3) × [(1/2 × 3² + 2×3) - (1/20² + 20)]
= (1/3) × [(9/2 + 6) - 0]
= (1/3) × (21/2)
= 7/2
Therefore, the average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Learn more about definite integral click;
https://brainly.com/question/30760284
#SPJ1
can anyone solve this?
6x^3 + 4x^2 - 10x
Answers
The answer is,
\(2x(3x + 5)(x - 1)\)
sorry if wrong.
ILL GIVE BRAINIEST ( or whatever that is)
why can't 3/4 be .34?
Answers
Answer:
3/4 would be .75
Step-by-step explanation:
1/4 would be .25 because .25x4=1. Because the denominator is a 4 you are trying to find a number that when multiplied 4 times would equal 1 or 4/4.
Answer:
3/4 cannot be .34 because that is not what it is equal to when converted to hundredths.
Step-by-step explanation:
The decimal 0.34 is in the value hundredths. 3/4's value when converted to hundredths is 75/100 or 0.75. We get this by multiplying 3 and 4 by the same factor that brings 4 to 100, which is 25.
So, 4*25=100(denominator), and 3*25=75(numerator). The decimal value is 0.75. Therefore, 3/4 cannot be 0.34 because the values are not the same.
ASAP!!! WILL MARK BRAINLIEST!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Apply the rules of exponents and solve leaving your answer in base-exponent form:
4^3 x 4^5 =
5^8 ÷ 5^-2 =
(6^3 ) ^ 4 =
Answers
B. 5^10
C. 6^12

If 1 pot of flowers holds
2
3
cup of dirt, how many cups are needed for 14 pots?
Write an expression to represent this problem.
14
×
2
3
Great job!
Answers
The expression 14 × 23 represents the total number of cups of dirt needed for 14 pots of flowers. By multiplying the number of pots (14) by the amount of dirt needed per pot (23), we find that a total of 322 cups of dirt are required to fill all 14 pots.
To calculate the total number of cups of dirt needed for 14 pots of flowers, we can use the expression 14 × 23.
Let's break down the problem and explain the steps involved.
Given information:
Each pot of flowers requires 23 cups of dirt.
We want to find the total number of cups of dirt needed for 14 pots.
To solve this, we can multiply the number of pots (14) by the number of cups of dirt required for each pot (23).
Expression: 14 × 23
When we multiply 14 by 23, we perform the following calculation:
14 × 3 = 42 (multiplying the units digit)
14 × 20 = 280 (multiplying the tens digit)
Summing the results: 280 + 42 = 322
Therefore, the total number of cups of dirt needed for 14 pots is 322 cups.
Let's analyze this further.
When we say that 1 pot of flowers requires 23 cups of dirt, it means that each individual pot needs a specific amount of dirt to be properly filled. Multiplying this amount by the number of pots (14) gives us the cumulative requirement for all the pots.
Using the expression 14 × 23, we are essentially multiplying the number of pots (14) by the amount of dirt needed per pot (23). This expression allows us to find the total quantity of dirt required to fill all 14 pots.
The multiplication process involves multiplying the units digit (4) of 14 by 3, which gives us 12. The result has a carry-over of 1, which we then multiply by the tens digit (2) of 14, resulting in 20. Finally, we add these two products (12 and 20) to obtain the final result of 322.
In conclusion, the expression 14 × 23 represents the total number of cups of dirt needed for 14 pots of flowers. By multiplying the number of pots (14) by the amount of dirt needed per pot (23), we find that a total of 322 cups of dirt are required to fill all 14 pots.
Learn more about expression here
https://brainly.com/question/1859113
#SPJ11
what is the slope of a line that is perpendicular to y = 2x + 3
a. 2
b. -2
c. 1/2
d. -1/2
Answers
Answer: The answer is: a
The equation of the directrix is (x=-2, x=2, y=2, y=-2?) and the focus is ( , ). This means that p=

Answers
Answer:
First question This parabola opens to the right so the standard form of the equation for this parabola is y^2 = 4px
for this question x=-2
2
0
2
for the third question The equation of the parabola is y^2 = 8x
Step-by-step explanation:
The equation for the parabola is y² = 4px, the equation of the directrix is x = -2, the focus is at (2, 0), and the value of p is 2.
What is a parabola?It is defined as the graph of a quadratic function that has something bowl-shaped.
(x - h)² = 4a(y - k)
(h, k) is the vertex of the parabola:
a = √[(c-h)² + (d-k²]
(c, d) is the focus of the parabola:
It is given that:
From the graph the equation will be:
y² = 4px
The focus is (2, 0)
As the directrix is x = -2
The value of p = 2.
Thus, the equation for the parabola is y² = 4px, the equation of the directrix is x = -2, the focus is at (2, 0), and the value of p is 2.
Learn more about the parabola here:
brainly.com/question/8708520
#SPJ2

Graph the following equations.
X=1

Answers

Answer:
Vertical line that passes over 1 the x axis. (No y-intercept)
Step-by-step explanation:
find the value of X, y and z
ans: x=50 y= 50 z=50

Answers
The value of x , y and z in the parallel line is 50 degrees.
How to find the angle in parallel line?When parallel lines are crossed by a transversal line, angle relationships are formed such as vertically opposite angles, alternate interior angles, alternate exterior angles, adjacent angles, corresponding angles etc.
Therefore, let's use the angle relationships to find the angle, x, y and z as follows:
Therefore,
x = 360 - 310(sum of angles in a point)
x = 50 degrees
Therefore,
x = y(alternate interior angles)
Alternate interior angles are congruent.
Hence,
y = 50 degrees
Therefore,
x = z(alternate interior angles)
z = 50 degrees.
learn more on angles here: https://brainly.com/question/17043791
#SPJ1
I need help with this question pls

Answers
Answer:
arc length formula :
Arc length = radius x central angle in radians.
Answer you seek : is 2 or B : pie inches
Step-by-step explanation:
According to the Woodlawn Park Zoo in Seattle, Washington, the average height
in inches (h) of a baby giraffe during its first week can be described by the
equation h = 72 + 1.2d, where d is the number of days since it was born.
Which statement explains the meaning of the 1.2 in the equation?

Answers
Answer:
the giraffe grows 1.2 inches a day
Step-by-step explanation:
x u y = {z l z ∈ x or z ∈ y} is a
Answers
X u y = {z l z ∈ x or z ∈ y} is a valid set builder notation. Yes, this is a valid set builder notation. This specifies the elements of the set.
A set builder notation is a way of expressing a set using a description of its elements. In this particular set builder notation, the set consists of all elements that are either in set x or set y.
The notation is written as {z l z ∈ x or z ∈ y}, where the curly braces denote the set and the statement "z ∈ x or z ∈ y" specifies the elements of the set. This is a valid set builder notation because it correctly expresses the elements of the set.
Learn more about set here
https://brainly.com/question/12979762
#SPJ4
there are two sets of dancers and a single pair must be randomly selected from each set. the first set consists of three men and one woman, and the second set consists of two women and one man. what is the probability that two men will be selected from the first set and two women will be selected from the second set?
Answers
The probability that two men will be selected from the first set and two women will be selected from the second set is 3/10 * 2/3, or 1/5.
The probability of selecting two men from the first set is 3/4. This is because there are 3 men in the first set and the probability of selecting one is 1/4. Since we need to select two, the probability of selecting both is 3/4 multiplied by itself, or 3/4 x 3/4. The probability of selecting two women from the second set is 2/3. This is because there are 2 women in the second set and the probability of selecting one is 1/3. Since we need to select two, the probability of selecting both is 2/3 multiplied by itself, or 2/3 x 2/3. The probability of selecting two men from the first set and two women from the second set is then 3/4 x 3/4 x 2/3 x 2/3, which is equal to 3/10 x 2/3, or 1/5.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ1
please help me 7th grade

Answers
Answer:
4(-80) = -320
Step-by-step explanation:
His elevation decreased by 80 each hour. Since he was walking for 4 hours, the equation would be
4(-80) = -320.
Jake buys a membership to the YMCA pool. He pays a membership fee of $36 and $2 each visit. Jake has another option to pay $8 each visit and no membership fee. After how many visits will the two plans be equal in cost?
Answers
2(6) + 36= 48
8x6=48
The area of a triangle is 18 square units and the length of the base is 4 units. What is the height of the triangle?
Answers
Answer:
I think it’s 9, not sure tho
Step-by-step explanation:
Answer:
The height of the triangle is 4.5 units.
Step-by-step explanation:
The formula for AREA is: L × W/H
So, if the length of the base is 4 units, we can say that if we divide 18 by 4, we will get the missing number (The height of the triangle).
3. A drawer contains a dozen brown socks and a dozen black socks, all unmatched. A man takes socks out at random in the dark. a) How many socks must he take out to be sure that he has at least two socks of the same color
Answers
The number of socks that must he take out to be sure that he has at least two socks of the same color is 3.
ProbabilityIn a situation were three (3) socks are taken from the drawer, at least two (2) socks must have the same color.
Using this formula
P=P(Red)+P(Black)+P(Either red or black)
Where:
P(Red)=1
P(Black)=1
P(Either red or black)=1
Hence:
P=1+1+1
P=3 socks
Therefore the number of socks that must he take out to be sure that he has at least two socks of the same color is 3.
Learn more about probability here:https://brainly.com/question/24756209
#SPJ1
In Virginia license plates have 7 letters. How many different plates can be made using all letters of the alphabet allowing repeating letters.
Answers
Answer:
26⁷ or 8031810176
Step-by-step explanation:
The alphabet has 26 letters, therefore we just multiply thr number of letters in the alphabet by the amount of letters in virginia license plates.
(6x+15)°
63° triangle

Answers
Answer:
x = 2
Step-by-step explanation:
The sum of the 3 angles in the triangle = 180°
Sum the 3 angles and equate to 180
6x + 15 + 90 + 63 = 180
6x + 168 = 180 ( subtract 168 from both sides )
6x = 12 ( divide both sides by 6 )
x = 2
In ΔKLM, k = 1.2 cm,
�
m∠L=93° and
�
m∠M=6°. Find the length of l, to the nearest 10th of a centimeter.
Answers
The length of LM is approximately 4.8 cm to the nearest 10th of a centimeter.
How to find angle of the triangle ?
To find the angle of a triangle, you need to know the lengths of its sides or the relationship between the lengths of its sides. There are different methods for finding angles depending on the information you have about the triangle. Here are a few examples:
Law of sines: If you know the lengths of two sides of a triangle and the angle between them, you can use the law of sines to find the angle opposite the longer side. The law of sines states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides. So, you can set up the equation:
sin(A) / a = sin(B) / b
where A and B are the angles opposite the sides a and b, respectively. Solve for the angle A to find the measure of the angle.
Law of cosines: If you know the lengths of all three sides of a triangle, you can use the law of cosines to find the angle opposite the longest side. The law of cosines states that:
c² = a² + b² - 2ab*cos(C)
where c is the length of the longest side (the side opposite angle C), and a and b are the lengths of the other two sides. Solve for cos(C) and then use the inverse cosine function to find the measure of angle C.
Right triangles: If you have a right triangle, you can use the properties of right triangles to find the angles. The sum of the measures of the two acute angles in a right triangle is always 90 degrees, so if you know one of the acute angles, you can find the other one by subtracting it from 90 degrees.
These are just a few methods for finding angles in a triangle. There are many other techniques depending on the specific information you have about the triangle.
To find the length of LM, we can use the law of sines which states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides. That is,
a/sin(A) = b/sin(B) = c/sin(C)
where a, b, and c are the lengths of the sides of the triangle and A, B, and C are the angles opposite those sides.
In this case, we know the length of KL is 1.2 cm, and we want to find the length of LM. Let's call the length of LM x. Then, we can use the law of sines to set up the following equation:
1.2/sin(93°) = x/sin(81°)
Solving for x, we get:
x = (1.2 × sin(81°)) / sin(93°)
Using a calculator, we get:
x ≈ 4.8 cm
Therefore, the length of LM is approximately 4.8 cm to the nearest 10th of a centimeter.
To know more about Triangles visit :-
https://brainly.com/question/17335144
#SPJ1
Answer:
draw a diagram, ASA law of sines, find another angle, plug in, opposite sides go together.
≈1.2133≈1.2
The question is below:

Answers
Answer:
(1, -4)
Step-by-step explanation:
Hope this helps!
i think i hope this helps
Part 1: Given cosine of theta is equal to radical 3 over 2 comma determine three possible angles θ on the domain [0,[infinity]). Part 2: Given θ = 495°, convert the value of θ to radians and find sec θ.
Answers
The required answer is sec θ = -√2.
Explanation:-
Part 1: Given cosine of theta is equal to radical 3 over 2 on the domain [0,[infinity]).
To determine three possible angles θ, the cosine inverse function which is a cos and since cosine function is positive in the first and second quadrant. Therefore conclude that, cosine function of θ = radical 3 over 2 implies that θ could be 30 degrees or 330 degrees or 390 degrees. So, θ = {30, 330, 390}.Part 2:To convert 495° to radians, multiply by π/180°.495° * π/180° = 11π/4To find sec θ, we use the reciprocal of the cosine function which is sec.
Therefore, sec θ = 1/cos θ.To find cos 11π/4, the reference angle, which is 3π/4. Cosine is negative in the third quadrant so the final result is sec θ = -√2.
To know about domain . To click the link.
https://brainly.com/question/30133157.
#SPJ11
if p(x) = x+ 7/ x-1 and q (x) = x^2 + x - 2, what is the product of p(3) and q(2)? a. 50 b. 45 c. 40 d. 20 e. 6
Answers
Answer:
d. 20
Step-by-step explanation:
To answer the question given, we will follow the steps below:
we need to first find p(3)
p(x) = x+ 7/ x-1
we will replace all x by 3 in the equation above
p(3) = 3+7 / 3-1
p(3) = 10/2
p(3) = 5
Similarly to find q(2)
q (x) = x^2 + x - 2,
we will replace x by 2 in the equation above
q (2) = 2^2 + 2 - 2
q (2) = 4 + 0
q (2) = 4
The product of p(3) and q(2) = 5 × 4 = 20
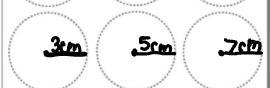
draw three circles with centre O and the radii of 3cm,5cm and 7cm
Answers
Answer:
you would make something like this:
Step-by-step explanation:
2) A gym charges a $30 membership fee and $10 per month. Write an
equation to represent this situation. Find the cost for 5 months. If a new
member paid $160, how many months did they go to the gym?
Answers
C = 10m + 30, where C is total cost and m is # of months
C = 10(5) + 30
C = 50 + 30
C = $80
$160 = 10m + 30
160 - 30 = 10m
130/10 = m
m = 13 months
Hope that helps
What is the equation f the line L that passes through the point (_2,2) and has slope 2? Select one: a.y = 2x + 5 b. y =2x -5 Cy = 2* - 2 d.y = 2x + 6
Answers
The equation of the line L that passes through the point (-2, 2) and has a slope of 2 is y = 2x + 6.
To find the equation of a line, we need to use the point-slope form, which is given by y - y₁ = m(x - x₁), where (x₁, y₁) represents a point on the line, and m is the slope. In this case, the given point is (-2, 2), and the slope is 2.
Substituting these values into the point-slope form, we get y - 2 = 2(x - (-2)), which simplifies to y - 2 = 2(x + 2). Distributing the 2 on the right side, we have y - 2 = 2x + 4.
To obtain the slope-intercept form of the equation, which is y = mx + b, we isolate y on the left side of the equation. Adding 2 to both sides, we get y = 2x + 6. Therefore, the equation of line L that passes through the point (-2, 2) with a slope of 2 is y = 2x + 6.
Learn more about line here:
https://brainly.com/question/21511618
#SPJ11
