PLEASE HELP! TRIGONOMETRY:
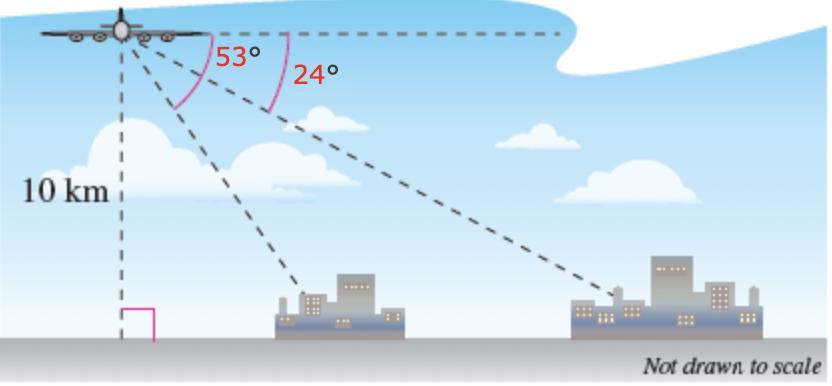
A passenger in an airplane at an altitude of 10 kilometers sees two towns directly to the east of the plane. The angles of depression to the towns are 24° and 53° (see figure). How far (in km) apart are the towns? (Round your answer to one decimal place.)

Hello!

area

= 2*25 + (20 - 2)*(25-8)

= 50cm² + 306cm²

= 356cm²

The required, in a reflection of triangle AB ≡ A'B' and ΔABC ≡ ΔABC are true.

AB ≡ A'B': True, because a reflection conserves length, so corresponding segments are congruent.

BC < B'C': False, in general, the length of conserves is preserved under a reflection, so BC = B'C'.

Triangle BACE = triangle B'A'C': True, because a reflection also conserves shape and size, so corresponding angles and sides are congruent.

∠BCA > ∠B'C'A': False, because the measure of an angle is not preserved under a reflection.

Learn more about congruent geometry here;

https://brainly.com/question/30293773

#SPJ1

The table of integrals can be a useful tool for simplifying the integration process, but it's important to have a solid understanding of calculus concepts in order to use it effectively.

The table of integrals is a tool used in calculus to simplify the process of finding antiderivatives. It lists various functions and their corresponding antiderivatives, or integrals.

To use the table of integrals, you first need to identify the function you are trying to integrate. Then, find a similar function in the table and use the corresponding antiderivative to solve your integral.

It's important to note that not all functions have a corresponding antiderivative listed in the table, and in those cases, other integration techniques must be used.

Additionally, it's always a good idea to double check your work and make sure the answer makes sense in the context of the original problem.

To learn more about : integrals

https://brainly.com/question/30094386

#SPJ11

If we use the table of integrals, the solution would be In | tan(x+7) + sec(x+7)|+C. Option A

Using the table of integral, we say

∫ (1/cos(x +7)) dx ⇒ ∫sec (x+7) dx

u = x+7   ⇒ du = dx

= ∫sec (u) du

Expand the fraction by tan (u) + sec (u)

= ∫(sec(u) (tan(u) + sec (u))/ tan (u) + sec (u)

= ∫((sec(u) tan(u) + sec²(u))/ (tan (u) + sec (u))) du

Substitute v= tan(u) + sec (u) ⇒ dv = (sec(u) tan(u) + sec²(u))du

= ∫(i/v)dv

= In(v)

Undo substitution v = tan(u) + sec(u)

=In(tan(u) + sec(u))

= In(tan(x+7) + sec(x +7))

Find more exercises on integrals:

https://brainly.com/question/14502499

#SPJ1

Answer:

6/11

Step-by-step explanation:

I don't know that's what my mom said

Answer:

Step-by-step explanation:

To find the area of the shaded region, we need to first find the x-coordinates of the points where the two functions intersect. We can set f(x) = g(x) and solve for x:

x^4 - 12x^3 + 48x^2 = 44x + 105

x^4 - 12x^3 + 48x^2 - 44x - 105 = 0

We can use a numerical method, such as the Newton-Raphson method, to approximate the roots of this equation. Using a graphing calculator or computer algebra system, we can find that the roots are approximately:

x = -1.932, x = 0.695, x = 4.149

Note that the root x = -1.932 is outside the given interval [3, 4], so we can ignore it.

The shaded region is bounded by the x-axis, the line y = 340, and the graphs of f(x) and g(x) between x = 3 and x = 4. To find the area of this region, we can integrate the difference between the two functions over this interval:

A = ∫3^4 [g(x) - f(x)] dx

A = ∫3^4 [44x + 105 - (x^4 - 12x^3 + 48x^2)] dx

A = ∫3^4 [-x^4 + 12x^3 - 48x^2 + 44x + 105] dx

We can integrate term by term using the power rule:

A = [-x^5/5 + 3x^4 - 16x^3 + 22x^2 + 105x]3^4

A = [-1024/5 + 192 - 192 + 22 + 105] - [-81/5 + 108 - 192 + 66 + 105]

A = 347.2

Therefore, the area of the shaded region is approximately 347.2 square units.

The graph of the function f(x) = 5(2)^x is an upward-sloping exponential curve that starts at (0, 5) and increases rapidly as x moves to the right, never crossing the x-axis.

The function f(x) = 5(2)^x represents exponential growth. Let's analyze its graph.

As x increases, the value of 2^x grows exponentially. Multiplying it by 5 further amplifies the growth. Here are a few key points to consider:

When x = 0, 2^0 = 1, so f(0) = 5(1) = 5. This is the y-intercept of the graph, meaning the function passes through the point (0, 5).

As x increases, 2^x grows rapidly. For positive values of x, the function will increase quickly. As x approaches positive infinity, 2^x grows without bound, resulting in the function also growing without bound.

For negative values of x, 2^x approaches zero. However, the function is multiplied by 5, so it will not reach zero. Instead, it will approach y = 0, but the graph will never touch or cross the x-axis.

The function is always positive since 2^x is positive for any value of x, and multiplying by 5 does not change the sign.

Based on these observations, we can conclude that the graph of f(x) = 5(2)^x will be an exponential growth curve that starts at (0, 5) and increases rapidly as x moves to the right, never crossing or touching the x-axis.

The graph will have a smooth curve that rises steeply as x increases. The rate of growth will be determined by the base, in this case, 2. The larger the base, the steeper the curve. The function will approach but never reach the x-axis as x approaches negative infinity.

for more question on graph visit:

https://brainly.com/question/19040584

#SPJ8

Answer:

6xy

Step-by-step explanation:

GCF of the given monomials consists of 3 parts:

Combined all, the greatest common factor is 6xy

Answer: Two correct representations of the inequality -3(2x - 5) < 5(2 - x) are:

-6x + 15 < 10 - 5x

-6x + 15 < -5x + 10

Both of the above are correct because they are equivalent to the original inequality.

Note that in order to get the above representation, I first applied distributive property on both sides of the inequality and then combined like terms on both sides.

Step-by-step explanation:

Answer:

-3

Step-by-step explanation:

6 tables are required. Each prime number attender should serve 3 customers each.

The prime numbers between 1 and 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

All the numbers other than prime numbers are composite numbers.

The composite numbers from 1 to 100 are: 1, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.

Now, as there are 25 primes and 75 composites in the group that visited the restaurant, we can calculate the number of tables required by dividing the number of people by the seating capacity of each table.

Each table has a seating capacity of 15, so the number of tables required will be: Number of tables = (Number of customers)/(Seating capacity of each table)Number of customers = 25 (the number of primes) + 75 (the number of composites) = 100Number of tables = 100/15 = 6 tables

Therefore, 6 tables are required.

Now, as each prime number attender has to serve an equal number of customers, we need to calculate how many customers each one should serve.

Each prime attender has to serve 75/25 = 3 customers each, as there are 75 composites and 25 primes.

Thus, each prime number attender should serve 3 customers each.

For more questions on prime number

https://brainly.com/question/145452

#SPJ8

Answer:

Ok, el jugador tiene:

J picas, 10 de tréboles.

En la mesa tenemos:

2 de corazones, 10 de diamantes, 10 de corazones, j de corazones y 5 de corazones.

Entonces, nosotros tenemos un full, que son tres 10 y dos J.

Ahora, en la mesa vemos una gran probabilidad de color, pero el full le gana al color, así que esto no nos amenaza.

Las combinaciones que le ganan al full son:

Poker (4 cartas iguales)

el único poker posible con las cartas de la mesa es si alguien tubiera 2 dieces en la mano, pero nosotros tenemos uno, así que hay un solo otro diez, entonces nadie puede tener poker.

Escalera de color u escalera real: (5 cartas seguidas del mismo palo.)

hay 4 corazones en la mesa, pero no estan a una distancia de de tal forma que nadie pueda hacer una escalera.

La única mano que nos podría empatar, es si otra persona también tubiera un diez y una jota.

Entonces no podemos perder esta mano, en el peor caso la podemos empatar. Esto implica que la mejor decisión es apostar todo.

Answer:

d=2-3a

Step-by-step explanation:

Solve for d by simplifying both sides of the equation, then isolating the variable.

3d+3a=4

Subtract 3 from each side of the equal sign:

d+3a=1

Subtract 3a-1:

d=2-3a

Hence d=2-3a is your final answer

Answer:

d = 2 - 3a

a = -d+2/3

Step-by-step explanation:

i didnt know which one u wanted to slove for but here are the answers and putting both equations would take to long so yea

lmk if this helped

The probability that four batteries connected in series will have a combined voltage of 60.8 or more volts is approximately 0.0228 or 2.28%.

To find the probability that four batteries connected in series will have a combined voltage of 60.8 or more volts, we need to use the concept of the Central Limit Theorem.

In this case, we know that the mean voltage of a single battery is 15 volts and the standard deviation is 0.2 volts. When batteries are connected in series, their voltages add up.

The combined voltage of four batteries connected in series is the sum of their individual voltages. The mean of the combined voltage will be 4 times the mean of a single battery, which is 4 * 15 = 60 volts.

The standard deviation of the combined voltage will be the square root of the sum of the variances of the individual batteries. Since the batteries are connected in series, the variance of the combined voltage will be 4 times the variance of a single battery, which is 4 * (0.2)^2 = 0.16.

Now, we need to calculate the probability that the combined voltage of four batteries is 60.8 or more volts. We can use a standard normal distribution to calculate this probability.

First, we need to standardize the value of 60.8 using the formula:

Z = (X - μ) / σ

Where X is the value we want to standardize, μ is the mean, and σ is the standard deviation.

In this case, the standardized value is:

Z = (60.8 - 60) / sqrt(0.16)

Z = 0.8 / 0.4

Z = 2

Next, we can use a standard normal distribution table or calculator to find the probability associated with a Z-score of 2. The probability of obtaining a Z-score of 2 or more is approximately 0.0228.

Therefore, the probability that four batteries connected in series will have a combined voltage of 60.8 or more volts is approximately 0.0228 or 2.28%.

Learn more about probability here:

https://brainly.com/question/23417919

#SPJ8

Approximately 17.65% of Ana's salary is withheld for taxes.

To calculate the percentage of Ana's salary that is withheld for taxes, we need to determine the amount of tax withheld and then express it as a percentage of her net salary.

Number of hours worked per week (H) = 25 hours

Hourly wage (W) = $10

Net salary (S) = $212.50

Calculate the total earnings before taxes:

Total earnings = Hours worked * Hourly wage

Total earnings = 25 hours * $10/hour

Total earnings = $250

Determine the amount of tax withheld:

Tax withheld = Total earnings - Net salary

Tax withheld = $250 - $212.50

Tax withheld = $37.50

Calculate the percentage of salary withheld for taxes:

Percentage withheld = (Tax withheld / Net salary) * 100

Percentage withheld = ($37.50 / $212.50) * 100

Percentage withheld ≈ 17.65%

Therefore, approximately 17.65% of Ana's salary is withheld for taxes.

for such more question on percentage

https://brainly.com/question/24877689

#SPJ8

Answer:

-2x/yz

Step-by-step explanation:

You can cancel out terms using division and properties of exponents. x^a/x^b = x^a-b

To find the average rate of change of the function f(x) = 1.85x^2 over the interval 10 ≤ x ≤ 20, we need to find the difference in the function values at the endpoints of the interval and divide by the length of the interval.

The function value at x = 10 is:

f(10) = 1.85(10)^2 = 185

The function value at x = 20 is:

f(20) = 1.85(20)^2 = 740

The length of the interval is:

20 - 10 = 10

So the average rate of change of the function over the interval 10 ≤ x ≤ 20 is:

(f(20) - f(10)) / (20 - 10) = (740 - 185) / 10 = 55.5

Rounding to the nearest tenth, the average rate of change of the function over the interval 10 ≤ x ≤ 20 is approximately 55.5.

Answer:

1. The 95% confidence interval for the difference between means is (-5.34, 11.34).

2. The standard error of (x-bar1)-(x-bar2) is 4.

\(s_{M_d}=\sqrt{\dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2}}=\sqrt{\dfrac{9.2195^2}{10}+\dfrac{9.4868^2}{12}}\\\\\\s_{M_d}=\sqrt{8.5+7.5}=\sqrt{16}=4\)

Step-by-step explanation:

We have to calculate a 95% confidence interval for the difference between means.

The sample 1, of size n1=10 has a mean of 45 and a standard deviation of √85=9.2195.

The sample 2, of size n2=12 has a mean of 42 and a standard deviation of √90=9.4868.

The difference between sample means is Md=3.

\(M_d=M_1-M_2=45-42=3\)

The estimated standard error of the difference between means is computed using the formula:

\(s_{M_d}=\sqrt{\dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2}}=\sqrt{\dfrac{9.2195^2}{10}+\dfrac{9.4868^2}{12}}\\\\\\s_{M_d}=\sqrt{8.5+7.5}=\sqrt{16}=4\)

The critical t-value for a 95% confidence interval is t=2.086.

The margin of error (MOE) can be calculated as:

\(MOE=t\cdot s_{M_d}=2.086 \cdot 4=8.34\)

Then, the lower and upper bounds of the confidence interval are:

\(LL=M_d-t \cdot s_{M_d} = 3-8.34=-5.34\\\\UL=M_d+t \cdot s_{M_d} = 3+8.34=11.34\)

The 95% confidence interval for the difference between means is (-5.34, 11.34).

Answer:

48

Step-by-step explanation:

48 is greater then 6×4.2

It's even

It's a multiple of 3

the difference is 4

The points that are a horizontal distance of 6 and a vertical distance of 2 from the origin are (6, 2), (-6, 2), (6, -2), (-6, -2)

Points are undefined terms in geometry, however they are used to represent the coordinate or location of items in a coordinate plane

The features of the point are given as:

Horizontal distance = 6

Vertical distance = 2

The above means that:

x = 6

y = 2

The points are then represented as:

(x, y) = ±(x. y)

So, we have

(x, y) = ±(6, 2)

When the above equation is expanded, we have

(x, y) = (6, 2), (-6, 2), (6, -2), (-6, -2)

Next, we plot the points on a coordinate plane

See attachment for the graph of the plane

Hence. the points that are a horizontal distance of 6 and a vertical distance of 2 from the origin are (6, 2), (-6, 2), (6, -2), (-6, -2)

Read more about points at:

https://brainly.com/question/17206319

#SPJ1

There are countless possibilities for shapes that are similar but not congruent to shape 1, as long as they maintain the same proportions and shape.

There are many shapes that are similar but not congruent to shape 1. Similar shapes have the same shape, but their sizes may be different. In contrast, congruent shapes have the same shape and size.

One example of a similar shape to shape 1 is a rectangle that is twice as long and half as wide. Another example could be a square that is three times larger in area than shape 1.

A parallelogram that has the same base as shape 1 but is three times as tall is also similar but not congruent.

To learn more about : congruent

https://brainly.com/question/29789999

#SPJ8

Answer:

D.The slope of the relationship between first floor square footage and price is more steep for homes near the beach than elsewhere in Tampa

Step-by-step explanation:

We can see from the output that was run in this regression that this variable has a positive coefficient. So the result is going to be interpreted to show an increase. Therefore d is the answer as it shows that these homes which are closer to the beach are steeper compared to those that are in other areas of tampa. It's necessary to always look out for the signs of the coefficient when interpreting a regression result

Answer:

x = 8\(\sqrt{2}\)

Step-by-step explanation:

The triangle is isosceles with legs congruent, both x

Using Pythagoras identity in the right triangle

x² + x² = 16²

2x² = 256 ( divide both sides by 2 )

x² = 128 ( take the square root of both sides )

x = \(\sqrt{128}\) = \(\sqrt{64(2)}\) = \(\sqrt{64}\) × \(\sqrt{2}\) = 8\(\sqrt{2}\)

Answer:

i think you have to find the value

Step-by-step explanation:

Answer:

\(N + M = \begin{pmatrix}17.3&7.3\\ -5.2&-1.6\\ -8.2&-4.7\end{pmatrix}\)

Step-by-step explanation:

\(\begin{pmatrix}9.1&7.9\\ -2.4&0.2\\ -5.8&1.4\end{pmatrix} +\begin{pmatrix}8.2&-0.6\\ -2.8&-1.8\\ -2.4&-6.1\end{pmatrix} =\begin{pmatrix}9.1+8.2&7.9-0.6\\ -2.4-2.8&0.2-1.8\\ -5.8-2.4&1.4-6.1\end{pmatrix}\)

Then

\(\begin{pmatrix}9.1&7.9\\ -2.4&0.2\\ -5.8&1.4\end{pmatrix} +\begin{pmatrix}8.2&-0.6\\ -2.8&-1.8\\ -2.4&-6.1\end{pmatrix} =\begin{pmatrix}17.3&7.3\\ -5.2&-1.6\\ -8.2&-4.7\end{pmatrix}\)

Answer:

Based on the given equation for earnings on a checking account, we can substitute the given values to find the customer's earnings for the month if her minimum balance is $2,000.00:

I = rB - sx - f

I = 0.0095($2,000.00) - 0(28) - $4.00

I = $19.00 - $4.00

I = $15.00

Therefore, the customer's earnings for the month if her minimum balance is $2,000.00 is $15.00. Option C is the correct answer.

Answer:

jbejrnejnerbejdnedn

Step-by-step explanation:

njr3nirn3jrnmrn3kjrn3rj

rnheufenuenjebef\

kejirnrejfe

fjeifne

It takes Noah and Andre two and a half hours to meet.

Two or more expressions with an Equal sign is called as Equation.

Given that Noah and Andre are 15 miles apart on a bike path when they start biking toward each other .

Noah rides at a constant speed of 4 miles per hour ,and Andre rides at a constant speed of 2 miles per hour .

We have to find how long does it take until Noah and Andre meet

4x+2x=15

6x=15

Divide both sides by 6

x=15/6

x=5/2=2.5

It would take 2.5 hours long to both meet.

Hence, It takes Noah and Andre two and a half hours to meet.

To learn more on Equation:

https://brainly.com/question/10413253

#SPJ6

Answer:

y -12 21 -1.5 -11 11 -2 -10 14 -2.5 -9 17 ?

Step-by-step explanation:

There must exist a vertex u in T such that the distance between u and v is at most (n-1)/2.

To prove the existence of a vertex u in tree T such that the distance between u and v is at most (n-1)/2, we can employ a contradiction argument. Assume that such a vertex u does not exist.

Since the number of vertices in T is odd, there must be at least one path from v to another vertex w such that the distance between v and w is greater than (n-1)/2.

Denote this path as P. Let x be the vertex on path P that is closest to v.

By assumption, the distance from x to v is greater than (n-1)/2. However, the remaining vertices on path P, excluding x, must have distances at least (n+1)/2 from v.

Therefore, the total number of vertices in T would be at least n + (n+1)/2 > n, which is a contradiction.

Hence, there must exist a vertex u in T such that the distance between u and v is at most (n-1)/2.

For more such questions on vertex

https://brainly.com/question/25651698

#SPJ8