Answers
Answer:
35
Step-by-step explanation:
To find a parallelograms area you must take the height and multiply it by the base but the height is only the line that goes straight up and is at a 90 degree angle with the base. So in this case its as follows:
5 x 7 = 35
Related Questions
Explain step by step please!! Find f’(x) for f(x)=sin^3(3x^2)

Answers
Answer:
Step-by-step explanation:
g(x) = [tan( 4x-1)]2
Two less than a number cubed
múltiple choices
2−x³
x² - 3
x³- 2
3-x²
Answers
The first one (2-x^3) is the correct one
An example of a cois 6 < 10, that is, 6 is less than 10. 1. If any positive number is added to both sides of this inequality, will the inequality sign between 6 and 10 change? Give at least three examples to support your answer. If any negative number is added to both sides of this inequality, will the sign between 2. 6 and 10 change? Give at least three examples to support your answer.
Answers
Answer:
No, the sign won't change. The sign will only change if you multiply each side by -1.
Step-by-step explanation:
adding negative numbers also won't change the sign. We can see this because we are adding the same numbers
6<10
10<14
2<6
-6<-2
PLZ HELP ME :( it is simliar triangles

Answers
Answer:
B
Step-by-step explanation:
i think
Classify each triangle by its sides.
3.
1)Scalene
2)isosceles
3)equilateral
4)acute

Answers
Answer:
1
Step-by-step explanation:
None of the sides are equal. Isosceles means that 2 sides are equal. Equilateral means that all sides are equal.
Find the value of x. Give reasons to justify your solution. D ∈ AC
Answers
Answer:
x = 13
Step-by-step explanation:
Find the diagram attached
From the diagram, the sum of angle of the straight line BCD is 180°. Hence;
<BCE+<ECF<90 = 180
<BCE+64+90=180
<BCE+154 = 180
<BCE = 180-154
<BCE = 26°
Next is to get x.
The sum of interior angles <BCE and <BEC is equal to exterior angle <ABE
<BCE + <BEC = <ABE
26+x = 3x
Collect like terms
26 =3x-x
26=2x
x = 26/2
x = 13
Hence the value of x is 13

Hector solves and equation by subtracting 8 from both sides of the equation. Then he multiples both sides of the equation by 3. The result is m=15. What was the original equation? How do you know?
Answers
Given:
The result is \(m=15\).
To find:
The original equation.
Solution:
We need to apply the opposite operations from bottom to top in the resultant equation to get the original equation.
It means opposite operation of last operation will be applied first.
We have,
\(m=15\)
Divide both sides by 3.
\(\dfrac{m}{3}=5\)
Add 8 on both sides.
\(\dfrac{m}{3}+8=5+8\)
\(\dfrac{m}{3}+8=13\)
Therefore, the original equation is \(\dfrac{m}{3}+8=13\).
Please help this is due today and I’m so stressed!I will mark Branliest!!!
Tanya performs two transformations on ABC to form A"B"C" as shown on the coordinate grid below.
True or False:ABC is similar to A”B”C”?

Answers
3x√64= please help meee
Answers
Answer:
I think the answer is 2.7
Step-by-step explanation:
3x√64
√64=8
3x=8
x=8/3
x=2.7
) 1. a company is manufacturing a new dietary supplement pill that promotes body fat reduction. a. the company will supply 60 pills for a price of $40 and will supply 100 pills for a price of $60. determine a linear supply function p = s(q), for this product. [note the variables to use with p = s(9), so do not give the answer using x and y] b. the demand for this new dietary supplement pill is 50 pills at a price of $47.50 and 80 pills at a price of $32.50. determine a linear demand function p = d(9), for this product. c. find the equilibrium price and quantity for the new dietary supplement pill.
Answers
The supply function is p = s(9) = -5q + 100, and the demand function is p = d(9) = 1.25q + 22.50. The equilibrium price is $35, and the equilibrium quantity is 40 pills.
a. To determine the linear supply function, we can use the given price and quantity combinations. When the company supplies 60 pills for $40 and 100 pills for $60, we can form two points: (60, 40) and (100, 60). Using these points, we can find the slope of the supply function, which is -5, and the y-intercept, which is 100. Therefore, the supply function is p = s(9) = -5q + 100, where p represents the price and q represents the quantity supplied.
b. To determine the linear demand function, we can use the given price and quantity combinations. When the demand is 50 pills at a price of $47.50 and 80 pills at a price of $32.50, we can form two points: (50, 47.50) and (80, 32.50).
Using these points, we can find the slope of the demand function, which is 1.25, and the y-intercept, which is 22.50. Therefore, the demand function is p = d(9) = 1.25q + 22.50, where p represents the price and q represents the quantity demanded.
c. The equilibrium price and quantity occur at the intersection of the supply and demand functions. By setting the supply function equal to the demand function and solving for q, we can find the equilibrium quantity. Plugging this value back into either the supply or demand function will give us the equilibrium price.
By solving the equations, we find that the equilibrium quantity is 40 pills and the equilibrium price is $35. At this price, the quantity supplied equals the quantity demanded, leading to market equilibrium.
Learn more about equilibrium here:
brainly.com/question/32516916
#SPJ11
4. The piece below is 4/5 of the whole ribbon. Complete the drawing to show the whole ribbon.

Answers
Based on the limited information, it can be deduced that 1/5 of the ribbon is not in view.
How to solveIn order to show the complete ribbon, we need to understand that in mathematical terms:
Since 4/5 of the ribbon is showing
This means that about 1- 4/5
= 1/5 of the ribbon is not in view.
With this knowledge, you can go ahead to complete your drawing, knowing that a full ribbon has a rectangular shape.
Read more about fractions here:
https://brainly.com/question/78672
#SPJ1
Please help I have no idea what the answer is
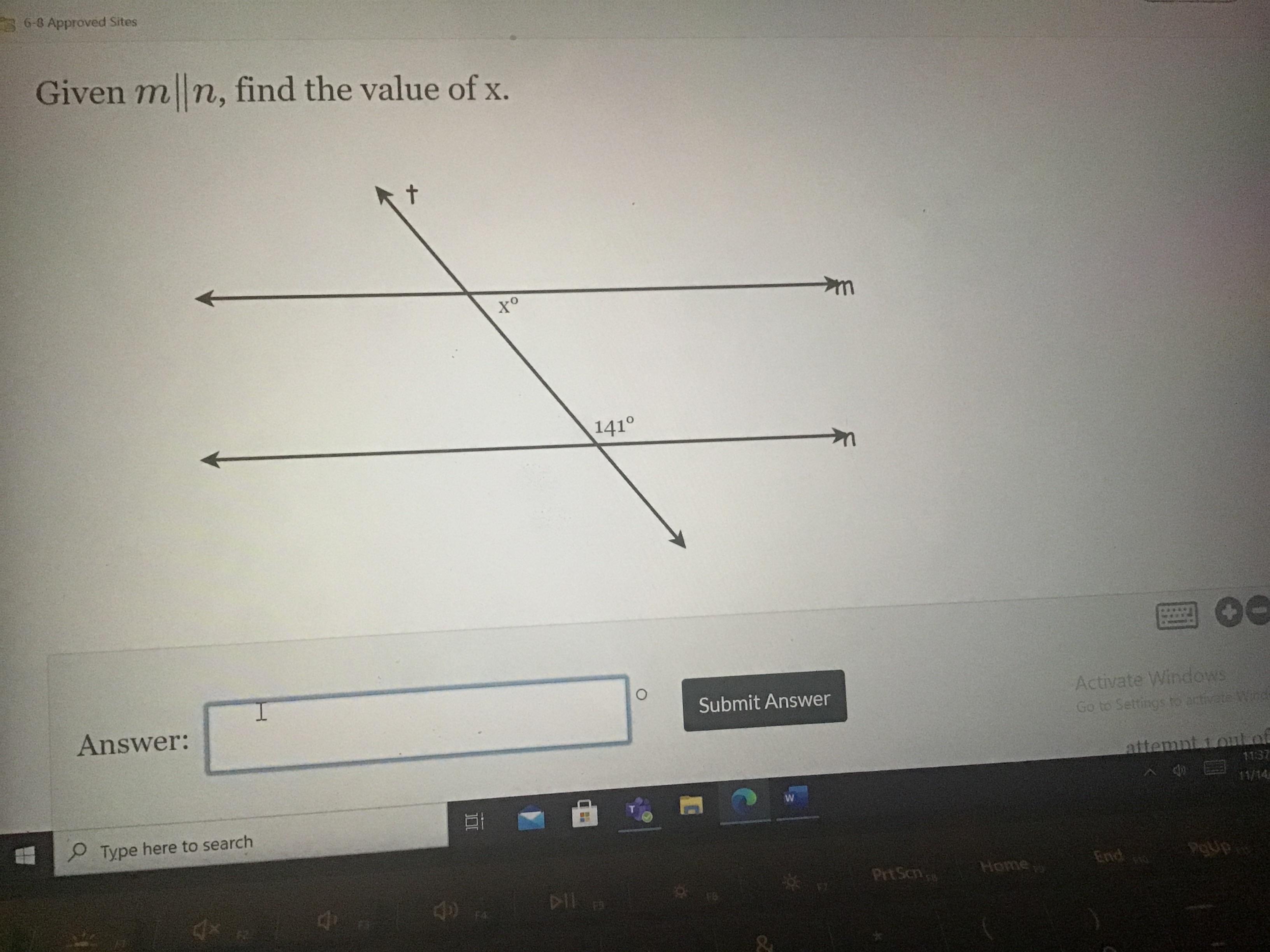
Answers
Answer:
39
Step-by-step explanation:
180 - 141 = 39
A straight angle equals to 180, since the lines are congruent, the angles have the same measurements.
Answer:
The value of x is 141° {Co interior angles}.
Step-by-step explanation:
Hope this helps you. Please mark me as Brainlist.
A rectangle has a length of 2x+7 and a width of 3x+8.
Write and simplify an expression for the perimeter of that rectangle
Answers
Answer:
2(2x+7)=4x+14
2(3x+8)=6x+16
4x+14+6x+16
4x+6x+14+16
The answer is:
10x+30
cindy is decorating a rectangular ballroom ceiling with garland. beginning in a corner, cindy strings garland along the length of the ceiling, a distance of 12 meters. next, cindy strings garland along the width of the ceiling, a distance of 16 meters. then cindy strings the garland straight back to the original corner. at this point, how much garland has cindy used?
Answers
Cindy used 48 meters of garland to decorate the rectangular ballroom ceiling by stringing it along the length of 12 meters, then the width of 16 meters, and finally back to the original corner.
To find out how much garland Cindy has used, use the Pythagorean theorem to determine the length of the diagonal, `d`, of the rectangular ballroom ceiling:
`d² = 12² + 16²`
= `d² = 144 + 256`
= `d² = 400`
= `d = √400`
= `d = 20`
Now that we have the length of the diagonal, `d`, we can determine the amount of garland Cindy has used. To do that, we just need to add up the three distances she has strung the garland:
`12 + 16 + 20 = 48`
Therefore, Cindy has used `48 meters` of garland.
To know more about Pythagorean theorem refer here:
https://brainly.com/question/14930619
#SPJ11
Pablo has $5,483 in a savings account. The interest rate is 5%, compounded annually.
To the nearest cent, how much will he have in 3 years?
(compound interest formu)
Answers
Answer:
$6347.26Step-by-step explanation:
Given:
Initial amount P = 5483Interest rate r = 5% or 0.05Compound number n = 1Time t = 3 yearsFind the total amount in 3 years:
\(A = P(1+r/n)^{nt}\)\(A = 5483*(1+0.05/1)^{1*3}=5483*(1.05)^3 = 6347.26\)Here we've been given,
Principal amount (p) = $5843 Compound number (n) = 1 Rate of Interest (r) = 5% = 5 × 1/100 = 0.05 Time (t) = 3 years A = ?The standard formula for Compound interest (C.P) is given by,
\(:\implies\tt{A = p( { \frac{1 + r}{n} )}^{n \times t} } \\ \\ \\ :\implies\tt{A = 5483( { \frac{1 + 0.05}{1}) }^{1 \times 3} } \\ \\ \\ :\implies\tt{A = 5483 \times {1.05}^{3} } \\ \\ \\ :\implies\tt{A = 6347.26}\)
4. Helena finds two pieces of a toy construction set that,
when joined together, make a rectangular prism. She
takes one piece away and is left with the piece shown
in the diagram.
Part A
When joined together, the original two pieces form a
rectangular prism with side lengths represented by the
expressions x + 4, 4x + 1, and 3x + 5. What is the volume
of that prism? Explain.
Part B
Find the volume of the construction piece shown in the diagram. Explain.

Answers
Answer:I belive the answer is 26 im not 100 percent sure tho been awhile since i did this
Step-by-step explanation:
Kesha borrowed $1,800 at 5% SIMPLE INTEREST. How much did Kesha owe after 6 months?
Interest: $
Total she owed: $
Answers
Answer:
Use Simple Interest Formula=PrT/100
SI=$1800×5×6/12÷100
=4500/100
=$45
Step-by-step explanation:
$45 is the interest that's gonna be owed after 6months so therefore the total $ she owed after 6 months would be: $45 + $1,800=$1,845.
USE BA II PLUS CALC TO SHOW WORK & FUNCTIONS
Question 2 – PV, Ordinary Annuity [2 points]: Find the present value of the following ordinary annuities:
$300 per year for 10 years at 10 percent interest rate
$100 per year for 5 years at 5 percent interest rate
Question 3 – PV, Annuity Due [2 points]: Find the present value of the following annuities due:
$300 per year for 10 years at 10 percent interest rate
$100 per year for 5 years at 5 percent interest rate
Answers
The present value of an ordinary annuity is $432.19. To calculate the present value of the first annuity, enter -300, 10, 0.10, and then press CPT and PV. The result will be $2,486.85.
The present value of an ordinary annuity is calculated by using the formula:
PV = PMT * [(1 - (1 + r)^-n) / r]
where PV is the present value, PMT is the payment per period, r is the interest rate per period, and n is the number of periods.
For the first ordinary annuity, with $300 per year for 10 years at a 10 percent interest rate:
PV = $300 * [(1 - (1 + 0.10)^-10) / 0.10] = $2,486.85
For the second ordinary annuity, with $100 per year for 5 years at a 5 percent interest rate:
PV = $100 * [(1 - (1 + 0.05)^-5) / 0.05] = $432.19
To calculate the present value of an ordinary annuity using the BA II Plus calculator, follow these steps:
1. Press the CF button.
2. Enter the payment amount as a negative value (-300 for the first annuity, -100 for the second annuity).
3. Press the ↓ key to move to the next cash flow entry.
4. Enter the number of periods (10 for the first annuity, 5 for the second annuity).
5. Press the ↓ key to move to the interest rate entry.
6. Enter the interest rate as a decimal (0.10 for the first annuity, 0.05 for the second annuity).
7. Press the CPT button.
8. Press the PV button to calculate the present value.
9. The result displayed is the present value of the annuity.
For example, to calculate the present value of the first annuity, enter -300, 10, 0.10, and then press CPT and PV. The result will be $2,486.85.
Repeat the same steps for the second annuity, using -100, 5, and 0.05 as the inputs. The result will be $432.19.
To know more about present value refer to:
https://brainly.com/question/30390056
#SPJ11
Hunter and his children went into a movie theater and will buy bags of popcorn and drinks. Each bag of popcorn costs $5.50 and each drink costs $6. Hunter has a total of $80 to spend on bags of popcorn and drinks. Write an inequality that would represent the possible values for the number of bags of popcorn purchased, bb, and the number of drinks purchased, d.d.
Answers
Answer:
......
Step-by-step explanation:
.......
Answer:
5.50b+6d≤80
Step-by-step explanation:
One bag of popcorn costs $5.50, so bb bags of popcorn cost 5.50b.5.50b. One drink costs $6, so dd drinks cost 6d.6d. The total 5.50b+6d5.50b+6d must be less than or equal to \$80:$80
if the output and input of a linear equation are proportional, whare will the graph of the equation cross the x axis
Answers
Answer:
at x=0 (the origin)
Step-by-step explanation:
The equation for a proportional relationship is ...
y = kx
The equation of a straight line is ...
y = kx +b . . . . . for some y-intercept b
Comparison to general lineComparing the proportional relation to the relation for a general line, we see that b=0 in the proportional relation. That is, the y-intercept is at y=0, the origin of the Cartesian coordinate plane.
The graph crosses the x-axis at (0, 0), or x=0.
__
Additional comment
In y=kx, the value k is called "the constant of proportionality." It is also the slope of the line on a graph.
In the usual representation of the slope-intercept equation of a line, y=mx+b, the slope of the line is represented by 'm'. In the above, we used 'k' for that purpose, to facilitate comparing the equations.
What is the slope of all lines parallel to the line
16x – 20y = -9?
Answers
Answer:
\(16x - 20y + 9 = 0\)
A senior class at Smith High School has 84 students.
The number of boys in the class is 4 more than the number of girls.
How many boys and girls are there in the class, respectively?
Answers
Answer: 44 boys and 40 girls
Step-by-step explanation:
x = number of girls
x + 4 = number of boys
x + x + 4 = 84
2x + 4 = 84
2x = 80
x = 40
84 - 40 = 44
Taylor will need cup of raisins
Answers
Answer:
yes get those raisins taylor
Step-by-step explanation:
woo! go taylor
in a circle with center o, central angle aob has a measure of 4 5π radians. the area of the sector formed by central angle aob is what fraction of the area of the circle?
Answers
The area of the sector formed by the central angle AOB is 9/2 (or 4.5) times the area of the circle.
The area of a sector is given by the formula:
Area of Sector = (θ/2π) * πr^2
Where θ is the central angle in radians, and r is the radius of the circle.
In this case, the central angle AOB has a measure of 4.5π radians.
The area of the sector formed by AOB is:
Area of Sector = (4.5π/2π) * πr^2
= (9/2) * πr^2
= 9/2 * πr^2
The total area of the circle is given by the formula:
Area of Circle = πr^2
To find the fraction of the area of the sector to the area of the circle, we divide the area of the sector by the area of the circle:
Fraction = (9/2 * πr^2) / (πr^2)
= (9/2)
learn more about fraction here:
https://brainly.com/question/10354322
#SPJ11
Problem Sathish is going on a 210021002100-kilometer road trip with 222 friends, whom he will pick up 150150150 kilometers after he begins the trip and drop off when there are 150150150 kilometers remaining. The car consumes 666 liters of gas for every 100100100 kilometers, and gas costs \$1.20$1.20dollar sign, 1, point, 20 per liter. Sathish will pay for all of the gas when he is alone in the car, but he and his friends will split the cost evenly when they are together.
Answers
Complete question :
Sathish is going on a 2100-kilometer road trip with 2 friends, whom he will pick up 150 kilometers after he begins the trip and drop off when there are 150 kilometer remaining. The car consumes 6 liters of gas for every 100 kilometers, and gas costs $1.20 per liter.
Sathish will pay for all of the gas when he is alone in the car, but he and his friends will split the cost evenly when they are together.
How much will Sathish pay for gas?
Answer:
$64.8
Step-by-step explanation:
Given that :
Total length of trip = 2100 km
Length of journey with Satish alone in the car:
(150km) beginning + (150km) ending = 300km
Length of journey with Satish and 2 friends :
2100 km - 300 km = 1800 km
Gas consumption:
6 liters per 100km
Cost of gas = $1.2 / litre
Consumption when Satish is alone :
(6 litres /100 km) * 300km = 18 litres
Cost = $1.2 * 18 = $21.6
Consumption with his 2 friends :
(6 litres /100 km) * 1800 km = 10800 / 100 = 108 litres
Cost = $1.2 * 108 = $129.6
Since amount is shared equally :
Amount paid by sattish = $129.6 / 3 = $43.2
Hence, total amount paid by Sattish is :
$21.6 + $43.2
= $64.8
Answer:
64.80 or 64.8
Step-by-step explanation:
whatever works <333
Find value of X please

Answers
Answer:
x=7
Step-by-step explanation:
Step #1- Set the two lines equal to each other
10+12=x+15
Step #2- Solve for the line you have all values for
10+12=22
Step#3- Plug 22 back into the equation where the two lines are set equal to each other
22=x+15
Step #4- Solve for X algebraically
22=x+15
22-15=x
7=x
A weather forecaster predicts that the May rainfall in a local area will be between three and six inches but has no idea where within the interval the amount will be. Let x be the amount of May rainfall in the local area, and assume that x is uniformly distributed over the interval three to six inches. (a) Write the formula for the probability curve of x. f(x) = / for < x < (b) What is the probability that May rainfall will be at least four inches? At least five inches?
Answers
The probability that May rainfall will be at least five inches can be calculated as: P(x ≥ 5) = (6-5) / (6-3) = 1/3
(a) The formula for the probability curve of x is:
f(x) = 1 / (6-3) = 1/3 for 3 ≤ x ≤ 6
This is because x is uniformly distributed over the interval three to six inches, which means that all values within the interval are equally likely to occur. The probability of any specific value of x occurring is therefore equal to the width of the interval (6-3 = 3) divided by the total length of the interval, which is 1/3.
(b) The probability that May rainfall will be at least four inches can be calculated as follows:
P(x ≥ 4) = (6-4) / (6-3) = 2/3
This is because the probability of x being greater than or equal to 4 is equal to the width of the interval from 4 to 6 (which is 6-4 = 2) divided by the total length of the interval (which is 6-3 = 3).
This is because the probability of x being greater than or equal to 5 is equal to the width of the interval from 5 to 6 (which is 6-5 = 1) divided by the total length of the interval (which is 6-3 = 3).
Know more about probability here;
https://brainly.com/question/30034780
#SPJ11
Renting a tool form Store A costs $9.75 per hour plus a fee of $188.55. Renting the same tool
form Store B costs $15.99 per hour with no additional fee. Which inequality could be
used to
find the minimum number of hours, h, a tool must be rented so that the cost of renting the tool
at Store A is less then the renting it at Sore B?
F 188.55 > 15.99 + 9.75h
G 15.99h > 188.55 + 9.75h
H 9.75h < 188.55 + 15.99h
J 15.99h < 188.55h + 9.75
Answers
Answer:
G 15.99h > 188.55 + 9.75h
Step-by-step explanation:
A rectangular prism has dimensions 2 cm by 2 cm by 3 cm. What are the surface area and volume?
Answers
We will plug in the values to get (v=2cm•2cm•3cm) —> (v=12cm cubed, written as 12cm^3)
Next we will find the surface area. The surface area is found with the sum of area of all of the sides.
Think of it as if the box was a hollow box, and you took apart each side and laid them flat.
2 sides of the rectangle will by 2cm by 2cm,
and 4 sides of the rectangle will by 2cm by 3cm.
2 sides • 2cm by 2cm = 8cm
4 sides • 2cm by 3cm = 24cm
8cm + 24cm = 32cm^2 total surface area
Answers:
V=12cm^3
SA=32cm^2
.At an Oregon fiber-manufacturing facility, an analyst estimates that the weekly number of pounds of acetate fibers that can be produced is given by the function: z = f(x, y) = 14500x + 4000y + 15x²y - 11x3 = Where: z = the weekly # of pounds of acetate fiber X = the # of skilled workers at the plant y = the # of unskilled workers at the plant Determine the following: A) The weekly number of pounds of fiber that can be produced with 18 skilled workers and 31 unskilled workers. Answer = pounds B) Find an expression (fx) for the rate of change of output with respect to the number of skilled workers. Answer = fx C) Find an expression (fy) for the rate of change of output with respect to the number of unskilled workers. Answer = fy D) Find the rate of change of output with respect to skilled workers when 18 skilled workers and 31 unskilled workers are employed. (Your answer will be a number.) Answer =
Answers
The rate of change of output with respect to skilled workers when 18 skilled workers and 31 unskilled workers are employed is 427.94.
Given, the function is z = f(x, y)
= 14500x + 4000y + 15x²y - 11x³
Where, z = the weekly # of pounds of acetate fiber
X = the # of skilled workers at the planty = the # of unskilled workers at the plant
(a) We are given the values of skilled workers and unskilled workers, we need to calculate the number of pounds of fiber that can be produced.
Put x = 18
and y = 31 in the given function
z = f(x, y)
= 14500x + 4000y + 15x²y - 11x³z
= 14500 (18) + 4000 (31) + 15 (18)² (31) - 11 (18)³
= 261180 lbs
Hence, the weekly number of pounds of fiber that can be produced with 18 skilled workers and 31 unskilled workers is 261180 lbs.
(b) We need to find an expression (fx) for the rate of change of output with respect to the number of skilled workers.
Differentiate the given function with respect to x.
z = f(x, y)
= 14500x + 4000y + 15x²y - 11x³∂z/∂x
= 14500 + 30xy - 33x²
= 14500 + 30y (x - 11x²/30y)fx
= ∂z/∂x = 14500 + 30y (x - 11x²/30y)
Hence, the expression (fx) for the rate of change of output with respect to the number of skilled workers is fx = 14500 + 30y (x - 11x²/30y).
(c) We need to find an expression (fy) for the rate of change of output with respect to the number of unskilled workers.
Differentiate the given function with respect to y.z
= f(x, y)
= 14500x + 4000y + 15x²y - 11x³∂z/∂y
= 4000 + 15x²
= 15 (x² + 267)fy
= ∂z/∂y
= 15 (x² + 267)
Hence, the expression (fy) for the rate of change of output with respect to the number of unskilled workers is fy = 15 (x² + 267).
(d) We need to find the rate of change of output with respect to skilled workers when 18 skilled workers and 31 unskilled workers are employed.
Put x = 18 and
y = 31 in the expression of fx.
fx = 14500 + 30y (x - 11x²/30y)
= 14500 + 30 (31) (18) - 11 (18)² / 31
= 14500 + 16740 - 12762/31
= 427.94
Hence, the rate of change of output with respect to skilled workers when 18 skilled workers and 31 unskilled workers are employed is 427.94.
To know more about rate of change visit:
https://brainly.com/question/29181688
#SPJ11
