Please solve this problem
I really want the answer
please give the correct answer

Answers
Answer:
Step-by-step explanation:
Use PEDMAS
125 ÷ (-5) * (-4) - 100 = (-25) * (-4) - 100
= 100 - 100
= 0
Related Questions
Find the coordinates of point bbb on \overline{ac} ac start overline, a, c, end overline such that ababa, b is \dfrac{2}{7} 7 2 start fraction, 2, divided by, 7, end fraction of acaca,
c
Answers
The coordinates of point bbb are \left(\dfrac{2a+7c}{9}, 0\right)left( 9 2a+7c , 0 right).
To find the coordinates of point bbb on \overline{ac}ac start overline, a, c, end overline, we need to use the formula for the division of a line segment in a given ratio. The formula is:
\begin{aligned} x &= \dfrac{x_1m+x_2n}{m+n} \\ y &= \dfrac{y_1m+y_2n}{m+n} \end{aligned}
Where m and n are the given ratio, and (x1, y1) and (x2, y2) are the coordinates of the two endpoints of the line segment.
In this case, the given ratio is \dfrac{2}{7}7 2 start fraction, 2, divided by, 7, end fraction, and the coordinates of the two endpoints are (x1, y1) = (a, 0) and (x2, y2) = (c, 0).
Plugging in the values into the formula, we get:
\begin{aligned} x &= \dfrac{a \cdot 2 + c \cdot 7}{2+7} \\ y &= \dfrac{0 \cdot 2 + 0 \cdot 7}{2+7} \end{aligned}
Simplifying the equations, we get:
\begin{aligned} x &= \dfrac{2a+7c}{9} \\ y &= 0 \end{aligned}
Learn more about coordinates:
https://brainly.com/question/20935031
#SPJ11
IV Find the citical points at which profit (pie) is maximized given the total revenue TR=4700−302 and Total CostTC =320/10,500 (2pts) 1. Compute Marginal Revenue and Marginal Cost 2. Equate MR=MC to find Q
∗
3. Verify that Q* is a relative maximum point 4. Compute the maximum profit level (pie) )
∗
by establishing (pie)* =9( (pie) (Q
∗
)
Answers
To find the critical points at which profit is maximized given the total revenue TR = 4700 - 302 and total cost TC = 320/10,500, we need to compute the marginal revenue and marginal cost, equate MR = MC to find the optimal quantity Q∗, verify if Q∗ is a relative maximum point, and compute the maximum profit level (π) by evaluating π∗ = 9(π(Q∗)).
Marginal Revenue (MR) is the derivative of the total revenue function with respect to quantity (Q). In this case, MR = dTR/dQ. By taking the derivative of TR = 4700 - 302 with respect to Q, we can find the expression for MR.
Marginal Cost (MC) is the derivative of the total cost function with respect to quantity (Q). In this case, MC = dTC/dQ. By taking the derivative of TC = 320/10,500 with respect to Q, we can find the expression for MC.
To find the optimal quantity Q∗, we equate MR and MC by setting MR = MC and solve for Q. This is because profit is maximized when MR equals MC.
Once we have found Q∗, we need to verify if it is a relative maximum point. This can be done by checking the second derivative of the profit function and determining if it is negative at Q∗. If the second derivative is negative, it confirms that Q∗ is a relative maximum point.
Finally, to compute the maximum profit level (π∗), we evaluate π(Q∗) by substituting Q∗ into the profit function. In this case, we can multiply the value of π(Q∗) by 9 to obtain the maximum profit level (π∗).
Learn more about relative maximum point here:
https://brainly.com/question/32310828
#SPJ11
how much interest is earned on $1470 at 4% for six months
Answers
Answer:
$29.4
Step-by-step explanation:
I assume the question is based on simple interest since you didn't specify
Using simple interest
Simple interest=P×R×T
Where,
P=principal=$1470
R=interest rate=4%=0.04
T=time=6 months=0.5 year
Simple interest=P×R×T
=1470×0.04×0.5
=29.4
Interest earned=$29.4
Angle
x
= 076° and angle
y
= 111°.
Find the bearing of point A from point O.
Answers
The bearing of point A from point O is 256°.
What are bearings?In mathematics, a bearing is the angle in degrees measured clockwise from north. Bearings are usually given as a three-figure bearing. For example, 30° clockwise from north is usually written as 030°.
Given that, angle x= 076° and angle y = 111°.
Now, the bearing of point A from point O is
180°+ 076°
= 256°
Therefore, the bearing of point A from point O is 256°.
Learn more about the bearings here:
https://brainly.com/question/27962362.
#SPJ1

The function u= x2 - y2 + xy is harmonic FALSE TRUE
Answers
The function u = \(x^2 - y^2 + xy\) is not harmonic.
To determine if a function is harmonic, we need to check if it satisfies the Laplace's equation, which states that the sum of the second partial derivatives of a function with respect to its variables should be zero. In the case of a function u(x, y), the Laplace's equation is given by ∂^2u/∂x^2 + ∂^2u/∂y^2 = 0.
Let's compute the second partial derivatives of u = x^2 - y^2 + xy. Taking the partial derivatives with respect to x, we have ∂^2u/∂x^2 = 2 and ∂^2u/∂y^2 = -2. The sum of these partial derivatives is not zero, as 2 + (-2) ≠ 0. Since the Laplace's equation is not satisfied for u = x^2 - y^2 + xy, we conclude that the function is not harmonic. Harmonic functions are important in mathematical analysis and physics, as they have various applications, but in this case, u = x^2 - y^2 + xy does not meet the criteria to be considered harmonic.
Learn more about function here:
https://brainly.com/question/31062578
#SPJ11
Question 6 (5 points)
Determine if the given sequence represents a geometric sequence. If so, find the
common ratio.
3,9, 27, 81, ...
OA) 6
OB) 9
OC) /
OD 3
Can someone help me this is timed I need help
Answers
3, 9, 27, 81
Answer: 3
Ms. murphy has to select 4 swimmers out of 9 swimmers to create a relay team. in how many ways can she create a relay team?
Answers
Ms. murphy has to create a relay team in 3024 ways.
What is combination?
A combination is a collection of components produced under a certain set of constraints and conditions.
Selections are another name for combinations. The choice of items from a predetermined group of items corresponds to combinations. We don't want to organize anything here. We are going to choose them. We use the symbols n C r to represent the number of distinct r-selections or combinations among a set of n items.
As given, Ms murphy has to select 4 swimmers out of 9 swimmers to create a relay team.
By using the combination formula we can find the number of ways to create a relay team.
\(C^{n}_r = \frac{n!}{(n-r)!}\)
Where,
n is the number of all objects and r is a number of selected objects.
Here, n = 9 and r = 4.
So,
\(C^{9}_4 = \frac{9!}{(9-4)!} = \frac{9!}{5!} = \frac{x}{y} = 3024\)
Therefore, she create a relay team in 3024 ways.
To know more about the combination, click on the link
https://brainly.com/question/1941169
#SPJ4
Identify the sampling technique used to obtain the following sample. the first 35 students leaving the library are asked how much money they spent on textbooks for the semester. Choose the correct sampling technique below. A. Systematic sampling B. Convenience sampling C. Cluster sampling D. Stratified sampling E. Random sampling
Answers
The sampling technique used to obtain the described sample is A. Systematic sampling.
In systematic sampling, the elements of the population are ordered in some way, and then a starting point is randomly selected. From that point, every nth element is selected to be part of the sample.
In the given scenario, the first 35 students leaving the library were selected. This suggests that the students were ordered in some manner, and a systematic approach was used to select every nth student. Therefore, the sampling technique used is systematic sampling.
To know more about sampling technique,
https://brainly.com/question/29076444
#SPJ11
Carla can fill 5 glasses with soda every 20 seconds. Complete the table using equivalent ratios.
Answers
Answer:
Glasses 12 : 48 because, when you do 20/5 it equals to 4 so, the ratio will equal to seconds = Glasses • 4
44 seconds = 11 glasses
Step-by-step explanation:
an experiment involves selecting a random sample of 256 middle managers for study. one item of interest is their annual incomes. the sample mean is computed to be $35,420.00. if the population standard deviation is $2,150.00, what is the standard error of the mean? rev: 12 23 2020 qc cs-245219 multiple choice $134.38 $144.61 $2,150.00 $8.40
Answers
The standard error of the mean for a sample of 256 middle managers, with a population standard deviation of $2,150.00 and a sample mean of $35,420.00, is approximately $134.38.
The standard error of the mean can be calculated using the formula: standard error = population standard deviation / square root of sample size.
Population standard deviation (σ) = $2,150.00
Sample size (n) = 256
Substituting these values into the formula, we can calculate the standard error of the mean:
Standard error = $2,150.00 / √256
Standard error ≈ $2,150.00 / 16
Standard error ≈ $134.38
Therefore, the standard error of the mean is approximately $134.38.
To know more about standard error refer here
https://brainly.com/question/15119664#
#SPJ11
the water in a drainpiipe is 18 cm deep. the width of the surface of the water is 48 cm. find the radius of the pipe
Answers
The radius of the pipe is approximately 8.13 cm.
To find the radius of the pipe, we can use the formula for the volume of a cylinder, which relates the depth of the water, the width of the surface, and the radius of the pipe.
The volume of a cylinder is given by the formula V = π\(r^2\)h, where V is the volume, r is the radius, and h is the height or depth.
In this case, we are given the depth of the water as 18 cm and the width of the surface as 48 cm.
Since the width of the surface is equal to the diameter of the pipe, we can use the formula for the diameter of a circle, which is twice the radius.
Therefore, the radius is half of the diameter, or r = 48/2 = 24 cm.
Using the formula for the volume of a cylinder, we can write the equation as V = π\((24)^2\)(18), where V is the volume.
We know that the volume is equal to the cross-sectional area of the pipe multiplied by the depth of the water.
The cross-sectional area is given by the formula A = π\(r^2\).
Now we can solve for the radius.
Rearranging the equation V = π\((24)^2\)(18), we get
\((24)^2\) = V/(π(18))
Solving for \((24)^2\), we find that the radius is approximately 8.13 cm.
Learn more about volume of a cylinder here:
https://brainly.com/question/15891031
#SPJ11
Describe the correlation between highway mileage and engine size

Answers
Answer:
As engine size increases, highway mileage decreases.
Step-by-step explanation:
x/4 +6 ≤ x+8 inequality
Answers
Answer:
Solution in photo
Step-by-step explanation:

if you take a loan out for 1,000$ and have 10 years without payment with a 12% interest rate what does it equal
Answers
The total accrued amount to pay back after 10 years on a loan of $1000 with a 12% interest rate is $2200.
What is the total accrued amount of the loan?The total accrued amount is the principal amount payable on a loan over a period with its accumulated interest in that period of time.
First, converting R percent to r (rate), a decimal.
r = R/100 = 12%/100 = 0.12 per year.
Solving our equation:
A = P( 1 + rt)
A = 1000(1 + (0.12 × 10))
A = $2,200.00
The total amount accrued, principal plus interest, from simple interest on a principal of $1,000.00 at a rate of 12% per year for 10 years is $2,200.00.
Learn more about finding the total accrued amount of a loan here:
https://brainly.com/question/19341720
#SPJ1
for the following grouped frequency distribution table, what is the width of each class interval? x f 20-29 2 30-39 5 40-49 4 50-59 1
Answers
The width of each class interval from the given grouped frequency distribution table is 9.
What is a class interval?In a frequency distribution, the numerical width of a class is referred to as the class interval. Data is organised into classes in a grouped frequency distribution. The class interval is determined by the difference between the upper and lower class limits.
The give class intervals are 20-29, 30-39, 40-49 and 50-59.
The size, or width, of a class interval is the difference between the lower and upper class boundaries and is also referred to as the class width, class size, or class length.
So, class width = Upper class - Lower class
29-20=9
39-30=9
Therefore, the width of each class interval is 9.
Learn more about the class interval here:
https://brainly.com/question/29027902.
#SPJ1
What is the sum of (x ^ 2 - 3x + 2) and (5x ^ 2 - 3x - 8)
Answers
Answer:
6x^2-6x-6
Step-by-step explanation:
(x^2-3x+2)+(5x^2-3x-8)
x^2+5x^2-3x+(-3x)+2+(-8)
6x^2-3x-3x+2-8
6x^2-6x+2-8
6x^2-6x-6
(10 points) Give the design of a counter. Use five JK flip/flops. Assuming the value inside the counter is 00100, what will be the value of the counter after two clock ticks
Answers
This is because each clock tick will cause the counter to increment by one, and the binary value of 00100 incremented twice becomes 00110.
To design a counter using five JK flip-flops, we can cascade them in a "ripple" configuration. The output of the first flip-flop will be connected to the clock input of the second flip-flop, the output of the second flip-flop will be connected to the clock input of the third flip-flop, and so on. The input to the first flip-flop will be the clock signal, and the J and K inputs of all five flip-flops will be connected to a common input (such as a switch or another logic gate) that can be used to set the initial value of the counter. Assuming the value inside the counter is 00100, after two clock ticks the value of the counter will be 00110.
Learn more about binary value here
https://brainly.com/question/30583534
#SPJ11
Study this Frequency Distribution Table (FDT) to answer the question below.
CL fi xi fixi
10 – 15 8 12.5 100 8 9.5 – 15.5
16 – 21 10 18.5 185 18 15.5 – 21.5
22 – 27 8 24.5 196 26 21.5 – 27.5
28 – 33 4 30.5 122 30 27.7 – 33.5
n = 30 ∑ =603
n/2 = 30/2 = 15 i = 6
What is the Mode ?
(Use up to one decimal place in writing your answer).
Answers
The mode is 18.5.
What is mode?
In statistics, there are most repeated value among the given set of data. Those are called mode. Among the given set of data, mode is the value which has the maximum frequency. Sometimes, it may be possible to have more than one value which has the equal maximum frequency.
Formula for mode for grouped data is given by:
Mode = l + [(f₁-f₀)/(2f₁-f₀-f₂)]×h.-------------------(1)
Where, l = lower class limit of modal class, h = class size, f₁ = frequency of modal class, f₀ = frequency of class preceding to modal class, f₂ = frequency of class succeeding to modal class.
In the given problem l= 15.5
f₀= 8
f₁= 10
f₂= 8
h= 6
Putting all the values in equation (1) we obtain mode
mode= 15.5 +{(10-8)/(2×10-8-8)} ×6
= 15.5+(2/4)×6
= 15.5+ 3
= 18.5
Hence, the mode is 18.5.
To know more about modes
https://brainly.com/question/27951780 from the link.
#SPJ9
Convert 4pi/5 to degrees.
Answers
Answer:
To convert radians to degrees, multiply by 180π , since a full circle is 360° or 2π radians. Cancel the common factor of π .
Answer:
144∘
Step-by-step explanation:
4π5⋅180∘π=144∘
Prove that a torus at R
3
is equivalent to the Cartesian product of two circles at R
2
that is, prove that a torus at R
3
is homeomorphic to S
1
×S
1
. Hint: Given a>b two positive reals, the torus at R
3
can be defined as the set: T={[(a+bcos∅)cosθ,(a+bcos∅)sinθ,bsin∅]∈R
3
∣0≤∅≤2π,0≤θ≤2π} Remember that the circle is defined as the set S
1
={(cosβ,sinβ)∈R
2
∣0≤β≤2π}
Answers
To prove that a torus at R3 is homeomorphic to S1 × S1, we can show that there exists a continuous bijection between the two spaces.
Let's consider the torus T defined as T={[(a+bcos∅)cosθ,(a+bcos∅)sinθ,bsin∅]∈R3 ∣0≤∅≤2π,0≤θ≤2π}. We need to construct a function that maps points in T to points in S1 × S1.
Define the function f: T -> S1 × S1 as follows:
f([(a+bcos∅)cosθ,(a+bcos∅)sinθ,bsin∅]) = ((cos∅, sin∅), (cosθ, sinθ))
To prove that f is a continuous bijection, we need to show two things:
1. f is well-defined: This means that for every point in T, f assigns a unique point in S1 × S1. Since the coordinates in T are uniquely determined by ∅ and θ, and the coordinates in S1 × S1 are uniquely determined by ∅ and θ, f is well-defined.
2. f is continuous: We can show that each component of f is continuous. Both the projection functions from T to S1 and from T to S1 × S1 are continuous, as they are compositions of trigonometric functions. Therefore, f is continuous.
Since f is a well-defined continuous function and it is bijective, we can conclude that T is homeomorphic to S1 × S1.
Learn more about homeomorphic at https://brainly.com/question/30095911
#SPJ11
Let X be a Binomial random variable with n=6 and p=0.2. Find the following quantities correct to 4 decimals. (a) P(3)=x. (b) P(X≤3)= (c) P(X>3)= (d) μ(X)= (e) Var(X)=
Answers
Binomial random variable with n=6 and p=0.
(a) P(3) ≈ 0.0819, (b) P(X ≤ 3) ≈ 0.7373, (c) P(X > 3) ≈ 0.2627, (d) μ(X) = 1.2, (e) Var(X) = 0.768
To solve these problems, we can use the formulas and properties associated with the Binomial distribution. Let's calculate each quantity step by step:
(a) P(3) = P(X = 3)
The probability mass function (PMF) for a Binomial distribution is given by the formula:
P(X = k) = C(n, k) × \(p^{k}\) × \((1-p)^{(n-k)}\)
where C(n, k) represents the binomial coefficient.
In this case, n = 6 and p = 0.2, so we can substitute these values into the formula:
P(X = 3) = C(6, 3) × (0.2)³ × (1 - 0.2)⁽⁶⁻³⁾
To calculate the binomial coefficient C(6, 3), we use the formula:
C(n, k) = n! / (k! × (n - k)!)
Let's calculate these values:
C(6, 3) = 6! / (3!× (6 - 3)!)
= 6! / (3! × 3!)
= (6 × 5 × 4) / (3 × 2×1)
= 20
Now we can substitute these values into the PMF formula:
P(X = 3) = 20× (0.2)³ × (1 - 0.2)⁽⁶⁻³⁾
= 20 ×0.008×0.512
≈ 0.0819
Therefore, P(3) ≈ 0.0819.
(b) P(X ≤ 3)
To calculate this probability, we sum the probabilities for X taking on values 0, 1, 2, and 3:
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
Using the PMF formula, we can substitute the values and calculate:
P(X ≤ 3) = C(6, 0) × (0.2)⁰× (1 - 0.2)⁽⁶⁻⁰⁾+
C(6, 1) × (0.2)¹ × (1 - 0.2)⁽⁶⁻¹⁾ +
C(6, 2) × (0.2)² × (1 - 0.2)⁽⁶⁻²⁾ +
C(6, 3) × (0.2)³ × (1 - 0.2)⁽⁶⁻³⁾
Calculating each term:
C(6, 0) = 6! / (0! × (6 - 0)!) = 1
C(6, 1) = 6! / (1! × (6 - 1)!) = 6
C(6, 2) = 6! / (2! × (6 - 2)!) = 15
C(6, 3) = 6! / (3! × (6 - 3)!) = 20
Substituting these values:
P(X ≤ 3) = 1 × (0.2)⁰ × (1 - 0.2)⁽⁶⁻⁰⁾ +
6× (0.2)¹ × (1 - 0.2)⁽⁶⁻¹⁾+
15 × (0.2)² × (1 - 0.2)⁽⁶⁻²⁾ +
20× (0.2)³ × (1 - 0.2)⁽⁶⁻³⁾
P(X ≤ 3) ≈ 0.7373
Therefore, P(X ≤ 3) ≈ 0.7373.
(c) P(X > 3)
Since P(X > 3) is the complement of P(X ≤ 3), we can calculate it as follows:
P(X > 3) = 1 - P(X ≤ 3)
= 1 - 0.7373
≈ 0.2627
Therefore, P(X > 3) ≈ 0.2627.
(d) μ(X) - Mean of X
The mean of a Binomial distribution is given by the formula:
μ(X) = n ×p
Substituting n = 6 and p = 0.2:
μ(X) = 6× 0.2
= 1.2
Therefore, μ(X) = 1.2.
(e) Var(X) - Variance of X
The variance of a Binomial distribution is given by the formula:
Var(X) = n × p × (1 - p)
Substituting n = 6 and p = 0.2:
Var(X) = 6 × 0.2 × (1 - 0.2)
= 0.96 × 0.8
= 0.768
Therefore, Var(X) = 0.768.
To summarize:
(a) P(3) ≈ 0.0819
(b) P(X ≤ 3) ≈ 0.7373
(c) P(X > 3) ≈ 0.2627
(d) μ(X) = 1.2
(e) Var(X) = 0.768
Learn more about Binomial distribution here:
https://brainly.com/question/29137961
#SPJ11
I'LL GIVE BRAINLIEST TO WHOEVER ANSWERS THE QUESTION CORRECTLY!!

Answers
Answer:
(a) show all sides to be congruent
(f + h)(x)
given f(x)= 3x-2x+4, g(x)= 8x-2, h(x)= 3x +2

Answers
Answer:
To find the answers, all I have to do is apply the operations (plus, minus, times, and divide) that they tell me to, in the order that they tell me to.
(f + g)(x) = f (x) + g(x)
= [3x + 2] + [4 – 5x]
= 3x + 2 + 4 – 5x
= 3x – 5x + 2 + 4
= –2x + 6
(f – g)(x) = f (x) – g(x)
= [3x + 2] – [4 – 5x]
= 3x + 2 – 4 + 5x
= 3x + 5x + 2 – 4
= 8x – 2
(f × g)(x) = [f (x)][g(x)]
= (3x + 2)(4 – 5x)
= 12x + 8 – 15x2 – 10x
= –15x2 + 2x + 8
\left(\small{\dfrac{f}{g}}\right)(x) = \small{\dfrac{f(x)}{g(x)}}(
g
f
)(x)=
g(x)
f(x)
= \small{\dfrac{3x+2}{4-5x}}=
4−5x
3x+2
My answer is the neat listing of each of my results, clearly labelled as to which is which.
( f + g ) (x) = –2x + 6
( f – g ) (x) = 8x – 2
( f × g ) (x) = –15x2 + 2x + 8
\mathbf{\color{purple}{ \left(\small{\dfrac{\mathit{f}}{\mathit{g}}}\right)(\mathit{x}) = \small{\dfrac{3\mathit{x} + 2}{4 - 5\mathit{x}}} }}(
g
f
)(x)=
4−5x
3x+2
Step-by-step explanation:
Look at the picture to answer.
Find the volume of the composite figure. Round the answer to the nearest tenth.
Volume = ____cm3

Answers
Answer:
around 433.1 cm
find the first shape's volume.
L x W x H method.
\(4 * 10 * 8 = 320cm\)
Length is eight, height is 4, and width is 10.
Now, the 2nd shape.
The formula of finding a sphere with a radius of 3 is V = 4/3\(pi^3\)
In that case, the answer should be an estimated 113.1
Add the two cm's together.
\(320 + 113.1 = 433.1\)
Please note that this is rounded to tenths place and estimated.
Please mark brainliest. Thanks! :)
First of all we will divide the figure in two shapes. One is hemisphere and other is a cuboid.
Volume of hemisphere:
\( \boxed{ \tt \:v = \frac{2}{3} \pi {r}^{3} }\)
Volume of cuboid:
\( \boxed{ \tt \: v = length \times breadth \times height}\)
\(\red{ \rule{35pt}{2pt}} \orange{ \rule{35pt}{2pt}} \color{yellow}{ \rule{35pt} {2pt}} \green{ \rule{35pt} {2pt}} \blue{ \rule{35pt} {2pt}} \purple{ \rule{35pt} {2pt}}\)
Volume of the hemisphere ⤵️r = 3 pi = 22/7\( \sf \dashrightarrow \: v = \frac{2}{3} \times \frac{22}{7} \times {3}^{3} \)
\( \sf \dashrightarrow \: v = \frac{2}{ \cancel3} \times \frac{22}{7} \times \cancel{27}\)
\( \sf \dashrightarrow \: v = 2 \times \frac{22}{7} \times 9\)
\( \sf \dashrightarrow \: v = \frac{396}{7} \)
\( \sf \dashrightarrow \: v = 56.6 \: {cm}^{3} \)
Volume of the cuboid ⤵️Length = 8cmBreadth = 10cmHeight = 4cm\( \bf \multimap \: v = 8 \times 10 \times 4\)
\( \bf \multimap \: v = 80 \times 4\)
\( \bf \multimap \: v = 320 \: {cm}^{3} \)
Now, Total volume ↯\( \rm \leadsto \: total \: volume = 56.6 + 320 \: {cm}^{3} \)
\( \rm \leadsto \: total \: volume = 376.6\: {cm}^{3} \)
If we round to the nearest tenth the total volume is ᭄
\( \rm \twoheadrightarrow volume = 380 \: {cm}^{3} \)
Ex. 3) Maddie sells $12 T-shirts at sporting events. The T-shirt company pays her a base pay of $45 for each
event plus a 15% commission on the sales revenue from the T-shirts that she sells. How many T-shirts would
she have to sell at an event to triple her base pay?
a. Write a function representing the total pay, p, for t T-shirts sold for this scenario.
Answers
Answer: The total pay, p, for Maddie selling t T-shirts at an event can be represented by the following function:
p(t) = 45 + 0.15(12t)
where the first term, 45, represents the base pay that Maddie receives for each event, and the second term, 0.15(12t), represents the commission that she earns based on the sales revenue from the T-shirts she sells. Since Maddie sells 12 T-shirts at each event, the total sales revenue from the T-shirts she sells is 12t, and the commission she earns is 15% of that revenue, or 0.15(12t).
To find the number of T-shirts Maddie would have to sell at an event to triple her base pay of $45, we need to solve the following equation:
p(t) = 3(45)
Substituting the expression for p(t) into this equation, we get:
45 + 0.15(12t) = 135
Simplifying and solving for t, we get:
1.8t = 90
t = 50
Therefore, Maddie would have to sell 50 T-shirts at an event to triple her base pay of $45.
Step-by-step explanation:
What is the difference between arithmetic and exponential growth.
Answers
Exponential growth that shows greater increases with passing time, creating the curve of an exponential function and Arithmetic growth takes place when a constant is being added such that the amount of addition remains constant.
The amounts added grow by a fixed rate of growth, expressed in percentages. Due to the fact that these remain constant while the amounts added rise, growth is then typically measured in doubling times.
Due to the fact that all populations of organisms have the potential to experience exponential growth, the concept of exponential growth is particularly intriguing in the field of population biology.
Learn more about Exponential and Arithmetic Growth at:
https://brainly.com/question/30168786
#SPJ4
PLEASE HELP 100 POINTS
write an equation of the horizontal line that passes through (-7,-10)
Answers
Answer:
y + 10 = 0
Step-by-step explanation:
Slope of horizontal line is zero (0)
m = 0
By point slope form of a line.
\(y-y_1 =m(x - x_1) \\ \\ y - ( - 10) = 0 \{x - ( - 7) \} \\ \\ y + 10 = 0 \{x + 7\} \\ \\y + 10 = 0 \\ \\ \)
Answer:
y = -10
Step-by-step explanation:
the length of a rectangle is 3 feet less than 4 times the width. if the perimeter is 84 feet, find the length and the width of the rectangle.
Answers
length: 33, width: 9
write it out as 4x-3(2) + 2x. simplify that and you gey 84= 10x-6. add the 6 over and you get x=9, this is your width. know you just do 4(9) - 3 to find length, which equals 33
Please help math find the measure angle x in the figure below
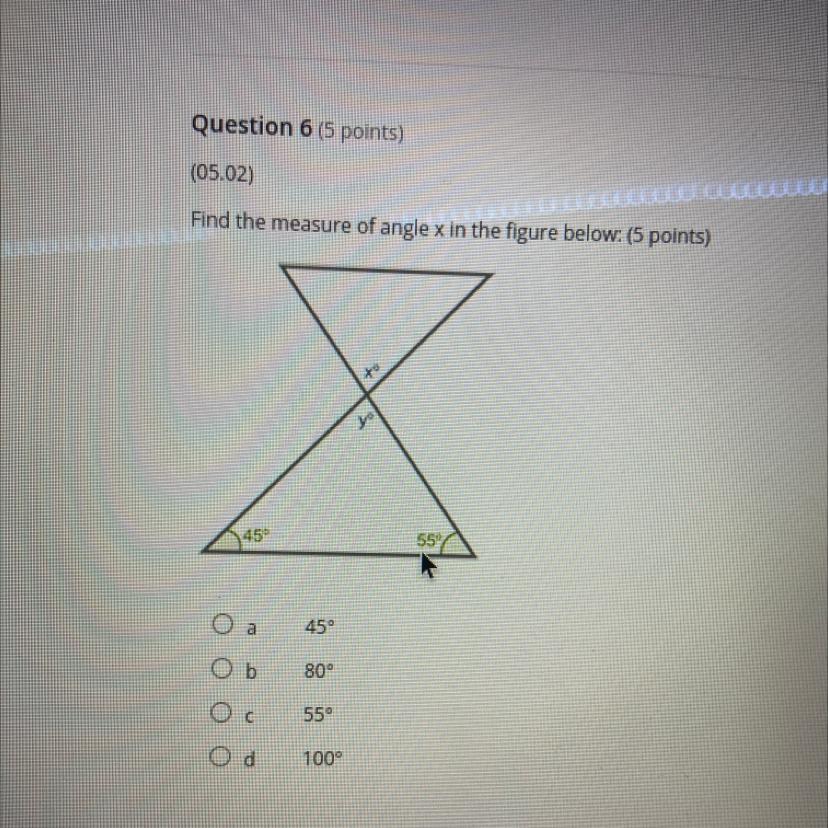
Answers
Answer:
Mm I didn't get the picture
a fair 6-sided die is rolled 10 times and the resulting sequence of 10 numbers is recorded, how many sequences are possible? how many different sequences consist entirely of even numbers? how many different sequences are possible if the first, third, and fourth numbers must be the same?
Answers
Using Combination,
a) Total 60,466,176 sequences are possible.
b) Total 59,049 different sequences consist entirely of even numbers.
c) Total 1,679,616 different sequences are possible if the first, third, and fourth numbers must be the same.
A fair die contain 6 numbers from 1 to 6.
sample space, S = { 1,2,3,4,5,6 }
a) 6 sided die is rolled 10 times
So, possible sequences = 6¹⁰
= 60,466,176
b) Even numbers in sample space = 3= { 2, 4,6}
The total possible sequences are 6¹⁰
So , we can conclude, then, that exactly half of those 6 to the power of 10 different possibilities would consist of solely even numbers, so that would be 3¹⁰ = 59,049 possible different sequence consists entirly even numbers.
The probability of getting a sequence of 10 even numbers = 3¹⁰/6¹⁰
= 0.000976563
c)one number from 6 that must be same for 3 places same can be selected ⁶C₁ ways
Remaining 7 places can be filled in 6⁷ ways
Hence required possible sequences are 6⁷x 6
= 6⁸= 1,679,616
Hence, we get all required different sequences.
a) 60,466,176 sequences
b)59,049 different sequences
c)1,679,616 different sequences
To learn more about combination, refer:
https://brainly.com/question/28065038
#SPJ4