PLEASE THIS IS URGENT!!
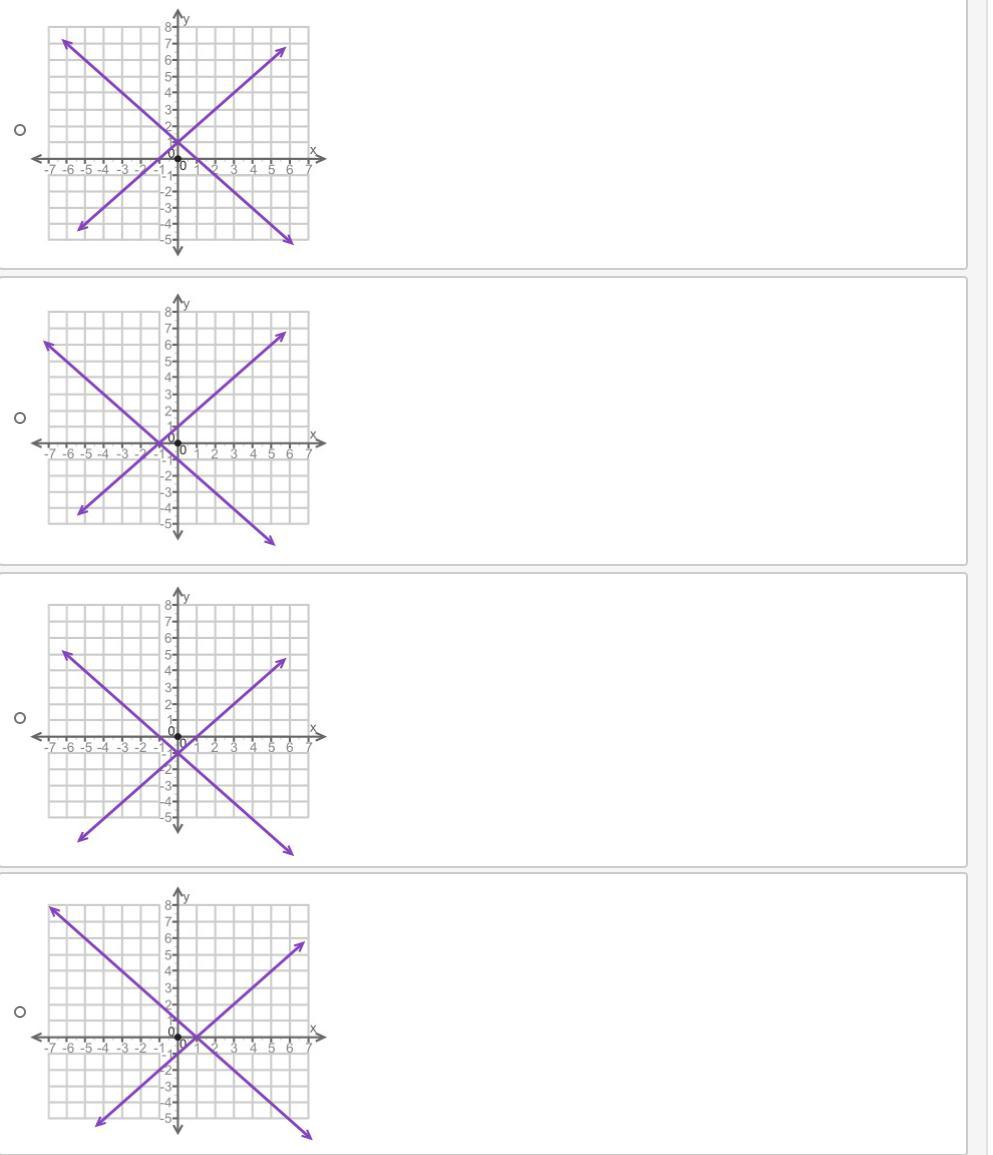
(08.02)Which of the following graphs best represents the solution to the pair of equations below?
y = x + 1
y = −x − 1
Answers
Answer:
The 2nd one. With the intersection to the left of the y-axis on the x-axis
Step-by-step explanation:
Related Questions
how many pairs of parallel sides does a rhombus have
Answers
A rhombus has two pairs of parallel sides.
A rhombus is a quadrilateral with four sides of equal length. A rhombus's opposite sides are parallel to one another. It has 2 diagonals that bisect each other at a 90-degree angle. In a rhombus, all sides are the same length. The opposite angles are congruent, but the adjacent angles are not. The adjacent angles have a sum of 180 degrees, as with all quadrilaterals.
A rhombus is a special type of parallelogram. A parallelogram is a four-sided figure with two pairs of parallel sides. A rhombus has two pairs of parallel sides because it is a type of parallelogram. However, all sides of a rhombus are of the same length. Furthermore, a rhombus's opposite angles are equal. This implies that if the diagonal of the rhombus bisects each other at a 90-degree angle, the diagonals are perpendicular.
Know more about Rhombus here :
https://brainly.com/question/29046794
#SPJ11

Preform the indicated operation. Be sure the answer is reduced.

Answers
2x+1
——-
X-8
Answer:
D. \(\frac{2x+1}{x-8}\)
Step-by-step explanation:
\(\frac{x+1}{x-8} - \frac{x}{8-x} = \\\\\frac{x+1 + x}{x-8} = \\\\\frac{x+1}{x-8} +\frac{x}{x-8} =\\\\\frac{x+1+x}{x-8} =\\\\\frac{2x+1}{x-8}\)
Correct choice is D
What is the LCD of - and -? 15 x 8 n 15 nx 75 x
Answers
Answer:
Answer 1
Step-by-step explanation:
Since 5 goes into 15x then 15x is the LCD, answer 1.
A snail moves at a speed of 2 feet per minute.
How many yards will the snail have moved in three quarters of an hour?
( please don’t say 3 for the speed because that’s definitely not my answer)
Answers
Answer: 29.7 miles!
Step-by-step explanation:
1 ft = 0.33 yard
The speed of the snail is 0.66 ft per minute
3 quartes of an hour is 45 minutes
So take 0.66 times 45 = 29.7 miles
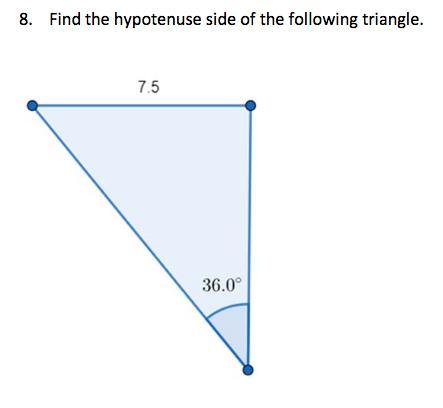
SOMEONE PLZ HELP ME ASAP!!!!
Answers
Answer:
hyp=12.76
Step-by-step explanation:
sin36=opp/hyp
hyp=opp/sin36
hyp=7.5/sin36
hyp=12.76 rounded to the nearest hundredth
What is the area of the hexagon?

Answers
Answer:
60m2
Step-by-step explanation:
Answer:
(d) 68 m²
Step-by-step explanation:
The figure can be decomposed into two congruent trapezoids, each with bases of 12 m and 5 m, and height 4 m. The formula for the area of a trapezoid can be used.
__
A = 1/2(b1 +b2)h . . . . . area of one trapezoid with bases b2, b2; height h
A = 1/2(12 m +5 m)(4 m) = 34 m²
The area of the hexagon is double this:
hexagon area = 2 × 34 m² = 68 m².
Consider the following IS-LM model: C=217+0.51Y_D I=156+0.16Y−1.038i G=254 T=203 i=0.04. The IS equation is determined to be Y=1,586.27−3,145.45i. The LM equation is given as i=0.04. Using the IS and LM equations, the equilibrium real output, Y, is (Round your response to the nearest integer.)
Answers
The equilibrium real output, Y, is approximately 1,460 (rounded to the nearest integer) in the given IS-LM model, using the provided IS and LM equations.
To find the equilibrium real output, we need to set the IS equation equal to the LM equation and solve for Y.
Given:
IS equation: Y = 1,586.27 - 3,145.45i
LM equation: i = 0.04
Substituting the LM equation into the IS equation:
1,586.27 - 3,145.45(0.04) = Y
Simplifying:
1,586.27 - 125.82 = Y
1,460.45 = Y
Therefore, the equilibrium real output, Y, is approximately 1,460 (rounded to the nearest integer).
To learn more about integer , click here:
brainly.com/question/33503847
#SPJ11
please help me i don't understand

Answers
Answer:
D and A
Step-by-step explanation:
1. 610:488 simplify
5:4
2.360:(488+551+610+360+391)
360:2400
3:20
Find F'(x): F(x) = Sx 3 t^1/3 dt
Answers
The derivative of F(x) is \(F'(x) = x^{(1/3)\).
What is function?A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output.
To find the derivative of the given function F(x), we will apply the fundamental theorem of calculus and differentiate the integral with respect to x.
Let's compute F'(x):
F(x) = ∫[0 to x] \(t^{(1/3)} dt\)
To differentiate the integral with respect to x, we'll use the Leibniz integral rule:
F'(x) = d/dx ∫[0 to x] \(t^{(1/3)} dt\)
According to the Leibniz integral rule, we have to apply the chain rule to the upper limit of the integral.
\(F'(x) = x^{(1/3)} d(x)/dx - 0^{(1/3)} d(0)/dx\) [applying the chain rule to the upper limit]
Since the upper limit of the integral is x, the derivative of x with respect to x is 1, and the derivative of 0 with respect to x is 0.
\(F'(x) = x^{(1/3)} (1) - 0^{(1/3)} (0)\)
\(F'(x) = x^{(1/3)\)
Therefore, the derivative of F(x) is \(F'(x) = x^{(1/3)\).
Learn more about function on:
https://brainly.com/question/7693326
#SPJ4
what is 463,462 rounded to the nearest ten?
Answers
Answer: 460,000
your welcome btw
Which fraction and decimal forms match the long division problem?

Answers
Answer: C
Step-by-step explanation: C
2 divided into 9 parts is 2/9.
Let's' explain this visually
Take this pizza, (image below)
Let's say we have two pizzas for 8 friends (including ourselves), so naturally, we'll cut the pizza's each into 9 slices, 1 for each, now everyone gets 1/9 of a pizza, but there are two pizzas, so if we add 1/9+1/9, we'll get two ninths.
Now 2/9=0.2 repeating!
This is how I got my answer sorry for the vague explanation

I’m confused on this

Answers
Answer:
x = 25
Step-by-step explanation:
The mistake here is the squaring. When you square one side, you have to do the same on the other side:
\(\sqrt{3x+6}\) = 9
\((\sqrt{3x+6}) ^{2}\) = \(9^{2}\)
3x + 6 = 81
3x = 75
x = 25
\(\huge\boxed{x=25}\)
The mistake is in Step 1. The solver should have also squared \(9\) when squaring the other side of the equation.
Correctly solving\(\begin{aligned}\sqrt{3x+6}&=9\\(\sqrt{3x+6})^2&=9^2\\3x+6&=81\\3x+6-6&=81-6\\3x&=75\\\frac{3x}{3}&=\frac{75}{3}\\x&=25\end{aligned}\)
Help please I NEED TO PASS :(((((

Answers
Answer:
The answer should be C
Step-by-step explanation:
I just got done calculating it and according to my calculations it should be C
5. A line has a slope of zero. Which of the
following points could this line pass through?
A. (12, 9) and (12, 6)
B. (3, -6) and (7,-6)
C. (1, 4) and (2, 5)
D. (-9, 7) and (9, -7)
Answers
Answer: The correct answer is B.
Step-by-step explanation:
In a line with a slope of 0 the x can change but the y cannot in a (x, y).
Consider the following linear programming problem: Maximise profit = 2X₁ - X₂ + 2X3 Subject to: 2X₁ + X₂ + 0x3 ≤10 X₁ + 2X₂ - 2X3 ≤ 20 0X₁ + X₂ + 2X3 ≤ 5 X₁ ,X2, X3 > 0 Change the objective function and constraints to simplex format by including the necessary additional variables.
Solve the problem above using the simplex method.
Answers
The linear programming problem is to maximize the profit function, given constraints, using the simplex method.
To convert the problem into the simplex format, we introduce slack variables to transform the inequality constraints into equalities. Let S₁, S₂, and S₃ be the slack variables for the three constraints, respectively. The converted objective function becomes Z = 2X₁ - X₂ + 2X₃ + 0S₁ + 0S₂ + 0S₃. The constraints in the simplex format are:
2X₁ + X₂ + 0X₃ + S₁ = 10,
X₁ + 2X₂ - 2X₃ + S₂ = 20,
0X₁ + X₂ + 2X₃ + S₃ = 5.
Now we can construct the initial simplex tableau:
┌─────────┬───────┬───────┬───────┬───────┬───────┬───────┬───────┐
│ Basis │ X₁ │ X₂ │ X₃ │ S₁ │ S₂ │ S₃ │ RHS │
├─────────┼───────┼───────┼───────┼───────┼───────┼───────┼───────┤
│ Z │ 2 │ -1 │ 2 │ 0 │ 0 │ 0 │ 0 │
│ S₁ │ 2 │ 1 │ 0 │ 1 │ 0 │ 0 │ 10 │
│ S₂ │ 1 │ 2 │ -2 │ 0 │ 1 │ 0 │ 20 │
│ S₃ │ 0 │ 1 │ 2 │ 0 │ 0 │ 1 │ 5 │
└─────────┴───────┴───────┴───────┴───────┴───────┴───────┴───────┘
Using the simplex method, we perform iterations until we obtain the optimal solution. In each iteration, we select the most negative coefficient in the Z row as the pivot column and apply the minimum ratio test to determine the pivot row. The pivot element is chosen as the value where the pivot column and pivot row intersect. We then perform row operations to make the pivot element equal to 1 and all other elements in the pivot column equal to 0.
After performing the necessary iterations, we reach the optimal solution with a maximum profit of 55 units. The values for the decision variables are X₁ = 0, X₂ = 5, and X₃ = 10. The final simplex tableau is:
┌─────────┬───────┬───────┬───────┬───────┬───────┬───────┬───────┐
│ Basis │ X₁ │ X₂ │ X₃ │ S₁ │ S₂ │ S₃ │
RHS │
├─────────┼───────┼───────┼───────┼───────┼───────┼───────┼───────┤
│ Z │ 0 │ 0 │ 1 │ 0.5 │ -1 │ -0.5 │ 55 │
│ X₂ │ 0.5 │ 0 │ 0 │ 0.5 │ -0.5 │ 0 │ 5 │
│ S₂ │ 0.5 │ 1 │ 0 │ -0.5 │ 0.5 │ 0 │ 15 │
│ X₃ │ -0.5 │ 0 │ 1 │ 0.5 │ 0.5 │ -0.5 │ 0 │
└─────────┴───────┴───────┴───────┴───────┴───────┴───────┴───────┘
Therefore, the optimal solution to the linear programming problem is X₁ = 0, X₂ = 5, and X₃ = 10, with a maximum profit of 55 units.
Learn more about simplex method here:
https://brainly.com/question/30970325
#SPJ11
use calculus to find two numbers whose difference is 100 and whose product is a minimum
Answers
The two numbers are -50 and 50. Their difference is 100, and their product is a minimum. We can calculate it in the following manner.
The question demands that we use calculus to find two numbers whose difference is 100 and whose product is a minimum. To do so, we must follow these steps: Let x and y be two numbers whose difference is 100. We can represent this as:y = x + 100
Since we want to find the minimum product of x and y, we can use the following formula: xy = x(x + 100) = x² + 100x
To find the minimum product, we must differentiate the expression and find the critical point. So, the first derivative of xy with respect to x is:dy/dx = 2x + 100= 0 => x = -50
The critical point is -50, so we need to check whether it is a minimum point. To do so, we can take the second derivative of xy with respect to x:d²y/dx² = 2It is positive, so the critical point is a minimum point. Therefore, the two numbers whose difference is 100 and whose product is a minimum are: x = -50 and y = -50 + 100 = 50
Finally we get (-50, 50)
To find two numbers whose difference is 100 and whose product is a minimum using calculus, let the two numbers be x and y. We are given:
y - x = 100
We want to minimize their product:
P(x, y) = x * y
We can solve for y in the difference equation:
y = x + 100
Now, substitute this expression for y into the product equation:
P(x) = x * (x + 100)
To find the minimum product, we need to find the critical points by taking the derivative of P(x) and setting it to zero:
dP(x)/dx = (x + 100) + x = 2x + 100
Set the derivative equal to zero:
2x + 100 = 0
Solve for x:
x = -50
Now, find the corresponding value of y:
y = x + 100 = -50 + 100 = 50
So, the two numbers are -50 and 50. Their difference is 100, and their product is a minimum.
Visit here to learn more about calculus brainly.com/question/6581270
#SPJ11
Look at the image. Type the correct answer. Use numerals instead of words.

Answers
Answer:
If the standard tax rate is 8.25%, how much money would a shopper save buying a $50 dress and a $30 pair of shoes during tax free week? Possible Answers: $2.47.
Step-by-step explanation:a
AC is a diameter of OE, the area of the
circle is 289 units2, and AB = 16 units.
Find BC and mBC.
B
A
C
E. plssss hurry !!

Answers
The measure of arc BC is 720 times the measure of angle BAC.
Given that AC is the diameter of the circle and AB is a chord with a length of 16 units, we need to find BC (the length of the other chord) and mBC (the measure of angle BAC).
To find BC, we can use the property of chords in a circle. If two chords intersect within a circle, the products of their segments are equal. In this case, since AB = BC = 16 units, the product of their segments will be:
AB * BC = AC * CE
16 * BC = 2 * r * CE (AC is the diameter, so its length is twice the radius)
Since the area of the circle is given as 289 square units, we can find the radius (r) using the formula for the area of a circle:
Area = π * r^2
289 = π * r^2
r^2 = 289 / π
r = √(289 / π)
Now, we can substitute the known values into the equation for the product of the segments:
16 * BC = 2 * √(289 / π) * CEBC = (√(289 / π) * CE) / 8
To find mBC, we can use the properties of angles in a circle. The angle subtended by an arc at the center of a circle is double the angle subtended by the same arc at any point on the circumference. Since AC is a diameter, angle BAC is a right angle. Therefore, mBC will be half the measure of the arc BC.
mBC = 0.5 * m(arc BC)
To find the measure of the arc BC, we need to find its length. The length of an arc is determined by the ratio of the arc angle to the total angle of the circle (360 degrees). Since mBC is half the arc angle, we can write:
arc BC = (mBC / 0.5) * 360
arc BC = 720 * mBC
Therefore, the length of the arc BC equals 720 times the length of the angle BAC.
for such more question on measure of arc
https://brainly.com/question/25716982
#SPJ8
Suppose that there are no restrictions on how many pages a printer can print. How many ways are there for the 100 pages to be assigned to the four printers
Answers
There are 176,851 ways to assign the 100 pages to the four printers.
Since there are no restrictions on how many pages a printer can print, we can think of this problem as distributing 100 identical pages among 4 distinct printers. This is an example of a "balls and urns" problem, which can be solved using the stars and bars formula.
The stars and bars formula states that the number of ways to distribute k identical objects among n distinct containers is:
C(k+n-1, n-1)
where C represents the combination function. In this case, we have k = 100 identical pages and n = 4 distinct printers. Therefore, the number of ways to assign the pages to the printers is:
C(100+4-1, 4-1) = C(103, 3) = 176,851
So there are 176,851 ways to assign the 100 pages to the four printers.
To learn more about statistics here
https://brainly.com/question/15525560
#SPJ4
help algebra 2 100 points if you answer right

Answers
the second one is the answer <i think>
\(\\ \tt\hookrightarrow (f+g)(x)\)
\(\\ \tt\hookrightarrow f(x)+g(x)\)
\(\\ \tt\hookrightarrow 4x^2-5x+3x^2+6x-4\)
\(\\ \tt\hookrightarrow 7x^2+x-4\)
Option B is correct
Metcalfe and Wiebe (1987) studied whether people could anticipate how close they were to solving algebra problems and the cheap necklace problem (an insight problem - also known as the chain problem). What was their main finding
Answers
Metcalfe and Wiebe (1987) conducted an experiment to examine whether individuals could predict how close they were to solving insight problems and algebraic problems. In insight problems, solutions are not immediately evident, whereas in algebraic problems, the correct solution is often clear but requires time to complete.
The primary objective of their research was to see whether people could anticipate when they would solve a problem, which would provide insight into the problem-solving process's nature.For their experiment, participants were given a series of algebraic and insight problems. After every ten seconds of problem-solving, they were asked to guess whether they were close to solving the problem.
Participants were less successful in predicting their progress on insight problems than on algebraic ones.
Participants were better able to forecast their progress on algebraic problems than on insight problems, according to the findings.
Participants who were more successful at solving insight problems were more likely to be able to predict their progress.
Participants were more likely to correctly anticipate their progress on the next few seconds of algebraic problems than on insight problems, according to the study's findings.
The research concluded that people's ability to predict their progress in insight problem-solving was worse than in algebraic problem-solving.
To know more about objective visit:
https://brainly.com/question/12569661
#SPJ11
What is 18/100 written as a decimal?
Answers
Answer:
18/100 as a decimal is:
0.18
Hope this helps! (づ ̄3 ̄)づ╭❤~
Step-by-step explanation:
Answer:
0.18
Step-by-step explanation:
18 divided by 100 is 0.18 18 divided by 1000 is 0.018
you move the decimal to the left when you divided a number by ten how many zeros is how many times you move the decimal. every number is a decimal like if you have a number 20 it actually looks like 20. so when you divide it by a 10 or 100 to move the decimal to the left the same number of zeros in 100 so that would be 0.20 hope you understand
Find Q 3 a. Q 3
=1 b. Q 3
=0.5 c. Q 3
=3 d. Q 3
=0 −5,−3,0,1,0,10,−2,−3,−1,3
Answers
The third quartile (Q3) for the given dataset (-5, -3, 0, 1, 0, 10, -2, -3, -1, 3) is 3.
To find the third quartile (Q3), we need to determine the value that separates the upper 25% of the data. The given dataset is: -5, -3, 0, 1, 0, 10, -2, -3, -1, 3.
To find Q3, we first need to arrange the dataset in ascending order: -5, -3, -3, -2, -1, 0, 0, 1, 3, 10.
Next, we calculate the position of Q3 using the formula: position = (3/4) * (n + 1), where n is the total number of data points. In this case, n = 10, so the position of Q3 = (3/4) * (10 + 1) = (3/4) * 11 = 8.25.
Since the position is not an integer, we take the average of the values at positions 8 and 9. The value at position 8 is 1, and the value at position 9 is 3. Therefore, the average of these two values gives us the third quartile (Q3): (1 + 3) / 2 = 4 / 2 = 2.
Hence, the third quartile (Q3) for the given dataset is 3.
Learn more about averages of quartile here:
https://brainly.com/question/31998489
#SPJ11
The graph of the function f(x) =x^2 is shown on the grid below. Graph the function g(x) =(x-2)^2 -4 in the interactive graph.

Answers
Answer:
shift it down by 4 units
Step-by-step explanation:
by the placement of the -4 it can be determined that you would shift it according to the y axis
The formula a(x-h)^2 + k = y
h represents change in x, k represents change in y
-k means shift down
Kiki works in a furniture store. Her base salary is $150 per day, plus an 8 percent commission on her sales. She sells several high-priced items. What is the total amount she earned over these three days?
Answers
Answer:
614
Step-by-step explanation:
Answer:
$614
Step-by-step explanation:
Does someone knows how to solve this. Step by step?
Completing the Square:
x^2-6x=15
Answers
Answer:
\(x_1=3+2\sqrt{6}\)
\(x_2=3-2\sqrt{6}\)
Step-by-step explanation
\(\rule{100mm}{0.5mm}\)
\(x^2-6x=15\)
\(x^2-6x+\left(\dfrac{6}{2}\right)^2-\left(\dfrac{6}{2}\right)^2=15\)
\(x^2-6x+3^2=15+3^2\)
\(x^2-6x+9=15+9\)
\((x-3)^2=24\)
\(\sqrt{(x-3)^2} =\sqrt{24}\)
\(x-3=\pm2\sqrt{6}\)
\(\red{\boxed{x_1=3+2\sqrt{6}}}\)
\(\red{\boxed{x_2=3-2\sqrt{6}}}\)
\(\rule {100mm}{0.5mm}\)
What is an equation of the line that passes through the point (4,2)(4,2) and is perpendicular to the line 4x+3y=214x+3y=21?
Answers
keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above
\(4x+3y=21\implies 3y=-4x+21\implies y=\cfrac{-4x+21}{3} \\\\\\ y=\stackrel{\stackrel{m}{\downarrow }}{-\cfrac{4}{3}}x+7\qquad \impliedby \qquad \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{\cfrac{-4}{3}} ~\hfill \stackrel{reciprocal}{\cfrac{3}{-4}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{3}{-4}\implies \cfrac{3}{4}}}\)
so we're really looking for the equation of a line whose slope is 3/4 and it passes through (4 , 2)
\((\stackrel{x_1}{4}~,~\stackrel{y_1}{2})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{3}{4} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{2}=\stackrel{m}{ \cfrac{3}{4}}(x-\stackrel{x_1}{4}) \\\\\\ y-2=\cfrac{3}{4}x-3\implies {\Large \begin{array}{llll} y=\cfrac{3}{4}x-1 \end{array}}\)
A house on the market was valued at $472,000. After several years, the value increased by 8%. By how much did the house's value Increase in dollars? What is
the current value of the house?
Answers
The house's value Increase in dollars by $37,760.
The current value of the house is $509, 760.
What is Percentage?To determine the quantity or percentage of something in terms of 100, use the percentage formula. Per cent simply means one in a hundred. Using the percentage formula, a number between 0 and 1 can be expressed. A number that is expressed as a fraction of 100 is what it is. It is mostly used to compare and determine ratios and is represented by the symbol %.
Given:
A house on the market was valued at $472,000.
After several years, the value increased by 8%.
Then, the value of house increased
= 472000 x 8/100
= $37,760
So, the current value of house
= 472000 + 37760
= $509, 760
Learn more about Percentage here:
https://brainly.com/question/29306119
#SPJ1
if cos theta is -4/7 and in the third quadrant, find the exact value of sin theta
Answers
In the third quadrant, the value of the cosine function is negative and so is the sine function.
Remember the identity
\(\sin ^2\theta+\cos ^2\theta=1\)Then,
\(\begin{gathered} \sin ^2\theta=1-\cos ^2\theta=1-(-\frac{4}{7})^2=1-\frac{16}{49}=\frac{33}{49} \\ \Rightarrow\sin ^2\theta=\frac{33}{49} \\ \Rightarrow\sin \theta=\pm\sqrt[]{\frac{33}{49}}=\pm\frac{\sqrt[]{33}}{7} \end{gathered}\)But remember that we are in the third quadrant; therefore, the value of sine has to be negative
\(\Rightarrow\sin \theta=-\frac{\sqrt[]{33}}{7}\)The answer is -sqrt(33)/7
If cos theta is -4/7 and in the third quadrant, the exact value of sin theta
5.74/7.
Now,
As we know,
sin²Ф + cos²Ф = 1
sin²Ф = 1 - cos²Ф
⇒ sinФ = √(1 - cos²Ф)
So,
cos²Ф = (-4/7)² = 16/49
so,
1-cos²Ф = 1-(16/49)=33/49
⇒ sinФ = (√33/√49)
sinФ =5.74/7
Learn more about trigonometry at :
https://brainly.com/question/4125724
Hi! If you could please do my assignment, I'd be grateful! I'll also mark brainliest, giving thanks, and hearts for the best. Thank you!!!

Answers
Answer:
1. AD
2. 5.2 cm
3. x = 4
4. BC
5. 3
6. x = 12
Step-by-step explanation: