Answers
The part of the proof that uses the justification that angles with a combined degree of 90° are complementary is; Congruent Complements Theorem
How to prove complementary angles?
We are given;
m∠1 = 40°
m∠2 = 50°
∠2 is complementary to ∠3
We want to prove that ∠1 ≅ ∠3
Now, when the sum of two angles equals 90°, they are called complementary angles.
Now, looking at the angles, the proof that ∠1 ≅ ∠3 is Congruent Complements Theorem. This is because If two angles are complements of the same angle (or congruent angles), then the two angles are congruent.
Read more about Complementary angles at; https://brainly.com/question/98924
#SPJ1
Related Questions
Brandon invested $11,000 in an account paying an interest rate of 1% compounded
quarterly. Robert invested $11,000 in an account paying an interest rate of 13/%
compounded monthly. After 20 years, how much more money would Robert have in
his account than Brandon, to the nearest dollar?
Answers
Answer: $4,914
Step-by-step explanation:
To calculate the final balance in Brandon's account, we need to use the formula for compound interest: A = P(1 + r/n)^(nt)
where A is the final balance, P is the initial investment, r is the interest rate, n is the number of times the interest is compounded per year, and t is the time in years.
In this case, we have:
P = $11,000
r = 1% = 0.01
n = 4 (because the interest is compounded quarterly)
t = 20
so, A = $11,000(1 + 0.01/4)^(4*20) = $11,000(1.0025)^80 = $22,817.20
To calculate the final balance in Robert's account, we need to use the same formula, but with different values for r, n, and t.
In this case, we have:
P = $11,000
r = 13/100 = 0.13
n = 12 (because the interest is compounded monthly)
t = 20
so, A = $11,000(1 + 0.13/12)^(12*20) = $11,000(1.01083333)^240 = $27,731.34
To find the difference in the final balances, we subtract the final balance in Brandon's account from the final balance in Robert's account:
$27,731.34 - $22,817.20 = $4,914.14
To the nearest dollar, the difference is $4,914.
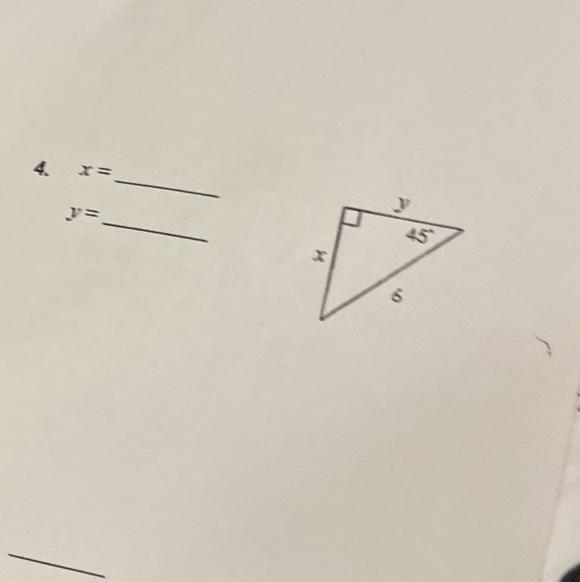
Answer:391
Step-by-step explanation:
find the value of each variable
x=
y=
Answers
A contractor needs to buy nails to build a house. The nails come in small boxes
and large boxes. Each small box has 50 nails and each large box has 450 nails.
The contractor bought twice as many small boxes as large boxes, which
altogether had 1100 nails. Determine the number of small boxes purchased
and the number of large boxes purchased.
Answers
The number of small boxes purchased is 4.
The number of large boxes purchased is 2.
The number of nails in a small box is 50, and the number of nails in a large box is 450.
The total number of nails bought is 1100.
Let the number of large boxes be "x".
The number of small boxes is "2x".
An equation is a formula in mathematics that expresses the equivalence of two expressions by linking them with the equal sign.
The equation can be formed as given below :
x*450 + 2x*50 = 1100
450x + 100x = 1100
550x = 1100
x = 2
The number of small boxes purchased is 2*x = 2*2 = 4.
The number of large boxes purchased is x = 2.
To learn more about equations, visit :
https://brainly.com/question/10413253
#SPJ1
Answer:
4 boxes of small nails.
2 boxes of large nails.
Step-by-step explanation:
Define the variables:
Let x = the number of small boxes of nails.Let y = the number of large boxes of nails.Given information:
Small box = 50 nails.Large box = 450 nails.The contractor bought twice as many small boxes as large boxes.Total number of nails bought = 1100 nails.Create a system of equations with the given information and defined variables:
\(\begin{cases}x=2y\\50x+450y=1100\end{cases}\)
Substitute the first equation into the second equation and solve for y:
\(\implies 50(2y)+450y=1100\)
\(\implies 100y+450y=1100\)
\(\implies 550y=1100\)
\(\implies \dfrac{550y}{550}=\dfrac{1100}{550}\)
\(\implies y=2\)
Substitute the found value of y into the first equation and solve for x:
\(\implies x=2(2)\)
\(\implies x=4\)
Therefore the contractor purchased:
4 boxes of small nails.2 boxes of large nails.4) Find the measure of the third angle.*
10 points
B
10 mm
540
5.9 mm
?
A
8.1 mm
60
35
36

Answers
Answer:
36
Step-by-step explanation:
angle A + angle B + angle C= 180°
180=90+54+angle A
angle A = 36
Answer:
b??? I think I'm so sorry if this is wrong I tried
Write the equation of a quadratic with the vertex at (2,-3) and passing through the point (6,4)
Answers
\(\displaystyle\\Answer:\ y=\frac{7}{16}x^2 -\frac{7}{4}x-\frac{5}{4}\)
Step-by-step explanation:
The vertex is also the symmetry point of the parabola. The formula for finding the x-coordinate of the parabola: x = -b/2a (2,-3)
Hence,
\(\displaystyle\\2=\frac{-b}{2a} \\\)
Multiply both parts of the equation by -2a:
\(\displaystyle\\-4a=b\ \ \ \ \ (1)\)
\(y=ax^2+bx+c\ \ \ \ \ -\ \ \ \ \ the\ quadratic\ equation\\\\Thus,\)
You can make a system of equations on two points belonging to the quadratic equation:
\(-3=a(2)^2+b(2)+c\\4=a(6)^2+b(6)+c\\\\-3=4a+2b+c\ \ \ \ (2)\\4=36a+6b+c\ \ \ \ (3)\\\\\)
Substitute (1) into equations (2) and (3):
\(-3=4a+2(-4a)+c\\4=36a+6(-4a)+c\\\\-3=4a-8a+c\\4=36a-24a+c\\\\-3=-4a+c\ \ \ \ (4)\\4=12a+c \ \ \ \ (5)\\\\\\\)
Subtract equation (4) from equation (5):
\(7=16a\)
Divide both parts of the equation by 16:
\(\displaystyle\\\frac{7}{16} =a\ \ \ \ (6)\)
Substitute (6) into equations (1):
\(\displaystyle\\-4(\frac{7}{16} )=b\\\\-\frac{4*7}{4*4}=b\\\\-\frac{7}{4}=b\)
Substitute values a and b into equation (2):
\(\displaystyle-3=4(\frac{7}{16})+2(-\frac{7}{4})+c\\\\ -3=\frac{7}{4} -\frac{14}{4}+c\\\\ -3=-\frac{7}{4}+c \\\\-3+\frac{7}{4}=-\frac{7}{4}+c+\frac{7}{4} \\\\ \frac{-3*4+7}{4} =c\\\\\frac{-12+7}{4}=c\\\\ -\frac{5}{4}=c\)
Thus,
\(\displaystyle\\y=\frac{7}{16}x^2 -\frac{7}{4}x-\frac{5}{4}\)
solve x2 - 10x = -21
Answers
Answer:
add 21 to both sides to get everything on one side
x^2 - 10x + 21 = 0
do factorization, guess and check
(x - 7) (x -3) = 0
x =7, and x =3
Answer:
x= 7,3
Step-by-step explanation:
Move all terms to the left side and set equal to 0. Then set each factor = to 0
Hope this helps please make me brainliest!
Question 10. State-Space (20 marks) (a) For a linear system with output y and input u below: + 2yy = 2u - uy i) Write the system state space model. ii) Find the equilibrium point(s) of the system if u is a constant value equal to 4. (b) Derive the state transition matrix of an autonomous linear system below: -2 x = Ax = - [ 3² ] ₁ X (c) Now, if a system has dynamic transfer function given below: x = Ax + Bu = [2²)x+ ₂ H U i) Determine the stability of the system. ii) Find the transfer function of the system. y = Cx= [1 −1] x
Answers
System state space model is: y = [1 0] x. y = 4 is an equilibrium point. x(t) = P∧(Dt)P−1 x(0) is the state transition matrix. The system is stable. The transfer function of the system is U(s)X(s) = [(s-2)²+ 4]⁻¹ [(s-2) -2; 2 (s-2)] [0 2].
(a) i) System state space model:
x = [y y']T;
dx/dt = [0 2; -1 1]x + [0 2]T u;
y = [1 0] x
Here, x represents the state vector.
ii) The equilibrium point(s) of the system if u is a constant value equal to 4: dy/dt = 0
Thus, 2y = 8 or y = 4. Therefore, y = 4 is an equilibrium point.
(b) The state transition matrix for autonomous linear systems is derived as follows:
If A is diagonalizable, then there exist an invertible matrix P and diagonal matrix D such that A = PDP−1.
Thus, x(t) = P∧(Dt)P−1 x(0) is the solution where exp(Dt) is calculated from the diagonal entries of D and t is the time of propagation.
(c) i)The stability of the system is determined by the eigenvalues of the system matrix A. If all the eigenvalues have a negative real part, the system is stable. If one of the eigenvalues has a positive real part, the system is unstable. And, if one eigenvalue has a zero real part, the system is marginally stable. Since the system has two eigenvalues with negative real parts, it is stable.
ii) The transfer function of the system is given as follows:
U(s) → X(s): X(s) = (sI − A)−1 B U(s)Y(s) → X(s): Y(s) = CX(s) = C(sI − A)−1 B U(s)
Thus, substituting the values of A, B, and C we get,Y(s) = [1 -1] [(s-2)²+ 4]⁻¹ [(s-2) -2; 2 (s-2)] [0 2]
U(s)X(s) = [(s-2)²+ 4]⁻¹ [(s-2) -2; 2 (s-2)] [0 2]
To know more about system state space model, visit:
https://brainly.com/question/32598929
#SPJ11
PLEASE HELP I'LL GIVE BRAINLIEST

Answers
Answer:a
Step-by-step explanation:
A ball is thrown from a height of 49 meters with an initial downward velocity of 2 m/s. The ball's height h (in meters) after t seconds is given by the following.
\(h=49-2t-5t^2\)
How long after the ball is thrown does it hit the ground?
Round your answer(s) to the nearest hundredth.
(If there is more than one answer, use the "or" button.)
Answers
A ball is thrown from an initial height of 6 feet with an initial upward velocity of 40ft/s . The ball's height h(in feet) after t seconds is given by the following. h=6+40t-16t^2 Find all values of t for which the ball's height is 28feet. Round your answer(s) to the nearest hundredth.
jen smith has decided to become her own boss after spending 5 years as an assistant manager for a restaurant. the owner of a local sandwich store wants to sell the store to jen for $65,000 to be paid in installments of $13,000 in each of the next 5 years. according to the current owner, the store brings in revenue of about $110,000 per year and incurs operating costs of about 63% of sales. thus, once the store is paid for, jen should make about $35,000 -$40,000 per year before taxes. until the store is paid for, she will make substantially less-but she will be her own boss. realizing that some uncertainty is involved in this decision, jen wants to simulate what level of net income she can expect to earn during the next 5 years as she operates and pays for the store. in particular, she wants to see what could happen if sales are allowed to vary based on a normal distribution with mean of $100,000 and standard deviation of $10,000, and if operating costs are allowed to vary uniformly between 60% and 65% of sales. assume that jen's payments for the store are not deductible for tax purposes and that she is in the 28% tax bracket. a. create a spreadsheet model to simulate the annual net income jen will receive during each of the next five years if she decides to buy the store. (3 points) b. given the money she has in savings; jen thinks she can get by for the next five years if she can make at least $12,000 from the store each year. run 100 simulation (replication) and find the probability that jen will make at least $12,000 in each of the next five years? (1 point) c. what is the probability (based on 100 simulation) that jen will make at least $60,000 total over the next five years? (1 point)
Answers
Jen simulated her net income over 5 years assuming sales vary based on a normal distribution $100,000 and operating costs 60% and 65% of sales. keeping the loan payment be fixed at $13,000. The probability of making at least $12,000 each year is the number of successful simulations divided by 100. and at least $60,000 total over 5 years based as the number of successful simulations divided by 100.
To simulate Jen's annual net income over the next 5 years, a spreadsheet model can be created with columns for year, sales, operating costs, loan payment, and net income.
For each year, the sales can be generated from a normal distribution with mean $100,000 and standard deviation $10,000, and the operating costs can be generated from a uniform distribution between 60% and 65% of sales.
The loan payment can be fixed at $13,000, and the net income can be calculated as the difference between the sales, operating costs, loan payment, and taxes (28% of net income).
To find the probability that Jen will make at least $12,000 in each of the next five years, 100 simulations can be run using the model created in part a. For each simulation, the net income for each of the next five years can be calculated, and if the minimum net income is at least $12,000 for each year, then the simulation is counted as a success.
The probability of success can be calculated as the number of successful simulations divided by 100.
To find the probability that Jen will make at least $60,000 total over the next five years, 100 simulations can be run using the model created in part a. For each simulation, the total net income over the next five years can be calculated, and if it is at least $60,000, then the simulation is counted as a success.
The probability of success can be calculated as the number of successful simulations divided by 100.
To know more about Probability:
https://brainly.com/question/11234923
#SPJ4
Callie has 3,264 beads. She wants to divide the beads evenly to make 32 necklaces. How many beads will be
used for each necklace?
Answers
Answer:
102 beads will be used for each necklace.
Step-by-step explanation:
3,264/32=102
Write the expression shown below in simplest terms.
4/5 (10x - 25) + 25
Answers
Answer:
4
0
−
1
0
0
5
+
2
5
Step-by-step explanation:
Brainliest?

Solve each equation for the other variable. (Hint: This will involve rewriting each equation in exponential form at some step in the process.)
a. y = log6(X)
b. X = log2(y/21)
Answers
The solution for the other variable, according to the stated statement, is\(X = 6^y\) and \(y = 21 * 2^X\)
What is an exponential number?Exponential numbers are represented by an, where an is multiplied by itself n times. An easy example is 8=2³=222. In exponential notation, an is known as the base, whereas n is known as the power, exponent, or index. Scientific notation is an example of an exponential number, with 10 usually typically serving as the base number.
Why is the term exponential used?Exponential functions are often employed in the biological sciences to describe the amount of a certain quantity over time, such as population size. Experiment data graphs are often created with time on the x-axis and amount on the y-axis.
a. y = log6(X)
\(6^y = X\)
\(X = 6^y\)
b. \(X = log2(y/21)\)
\(2^X = y/21\)
\(21 * 2^X = y\)
\(y = 21 * 2^X\)
To know more about exponential visit:
https://brainly.com/question/28596571
#SPJ1
(a) select one of the pairs of systems and write down its number. (b) for the pair selected, identify each system and state one function of that system. (c) explain how the two systems work together to help maintain homeostasis in an individual.
Answers
a. Pair 2 is selected.
b. Respiratory system, its function is to breathe. Digestive system, its function is to break down food into nutrients.
c. The two systems work together by sharing the region of the mouth and upper throat.
First picture in Pair 2 is Respiratory system, which its function is to breathe. Second picture in Pair 2 is Digestive system, which its function is to break down food into nutrients such as carbohydrates, fats and proteins. The respiratory system takes in oxygen from the air, and also gets rid of carbon dioxide. The digestive system absorbs water and nutrients from the food we consume.
How does the respiratory system and the digestive system work together?The respiratory system is mainly used to transport air, whilst the digestive system is used to transport fluids and solids, from water and food we eat. The respiratory and the digestive systems share the area of the mouth and upper throat, in which air, fluids, and solids can be mixed.
The digestive system does homeostasis by ensuring that the stomach area has the right pH balance. The body uses both positive and negative mechanisms to perform homeostasis. If the body detects an imbalance, the other systems work together to counterbalance and restore the right equilibrium.
Learn more about homeostasis at: https://brainly.com/question/3888340
#SPJ4

How many numbers can fit in a number place?
Answers
theres 1 number for each number place
i don’t know how to do this && i’m hella stuck

Answers
Answer:
C
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
I think
The rate at which crickets chirp is a linear function of
temperature. At 60°F they chirp 74 times per minute.
At 72º they chirp 120 times per minute.
a.) Write an equation in slope intercept form that
represents this function.
b.)Predict the number of chirps per minute when the
temperature is 64º.
Answers
Answer:
a) \(y=\frac{23}{6} x-156\)
b) \(\frac{268}{3}\)
Step-by-step explanation:
Formulas for linear equations:
Slope-intercept: \(y=mx+b\), where m is the slope and b is the y-intercept
Point-slope: \(y-y_1=m(x-x_1)\), where (x₁, y₁) is a point on the function and m is the slope.
a) We are given two points. If you're given two points (x₁, y₁) and (x₂, y₂), the slope m is given by the formula:
\(m = \frac{y_2-y_1}{x_2-x_1}\)
Let's mark the temperature on the x-axis, and the number of chirps per minute on the y-axis. So, we have the following points: (60, 74), and (72, 120). Calculating the slope m between these two points:
\(m=\frac{120-74}{72-60}\)
\(m=\frac{23}{6}\)
Since we have the x and y coordinates of a point on the function, we can write an equation in point-slope form, which will help us to find the y-intercept. We need the y-intercept in order to write the slope intercept form of the equation. We will use the point (60, 74) here, although you can also use (72, 120) if you want.
Point-slope form equation of the linear function:
\(y-74=\frac{23}{6} (x-60)\)
Now that we have the point-slope equation of the function, we can find the y-intercept. The y-intercept is the point on the function where the graph crosses the y-axis (when the x-value is 0). So, we plug in 0 for x into the equation and solve for y:
\(y-74=\frac{23}{6} (0-60)\)
\(y=-230+74\)
\(y=-156\)
Now that we have the y-intercept value of the function, we can write an equation in slope-intercept form:
\(y=\frac{23}{6} x-156\)
b) Since we marked the temperature on the x-axis, we can just plug in the number 64 as the x-value into the equation we have. y will be the number of chirps per minute when the temperature is 64º.
\(y=(\frac{23}{6} *64)-156\)
\(y=\frac{736}{3} - \frac{468}{3}\)
\(y=\frac{268}{3}\)
If you have any questions, leave a comment below.
Middle School
Mathematics
Find x.
A. 8
B. 12

Answers
Answer:
17²=15²+x²
289=225+x²
288-225=x²
64=x²
x=6
Answer:
8
Step-by-step explanation:
By Pythagoras theorem,
(hypotenuse)² = (altitude)² + (base)²
(17)² = x² + (15)²
(17)² - (15)² = x²
289 - 225 = x²
x² = 64
x = √64
x = 8
hope this helps you!
Problem - A car's gas tank holds 17 gallons. The car can be driven 425 miles on a single tank of gas. a. Write an equation which shows the relationship between the number of gallons of gasoline and the distance the car can be driven. b. How far can the car be driven if there is only 6.3 gallons of gas (rather than 15 gallons)? c. If the car is driven 14,000 miles in one year, how many gallons of gasoline were used? d. If the gasoline costs $4.10 per gallon, how much did it cost to purchase gasoline for the entire year. e. Compute miles per gallon. f. What is the gasoline cost per mile?
Answers
a) An equation to show the relationship between the number of gallons of gasoline and the distance driven is r = 25 mpg.
b) The total distance to be traveled using 6.3 gallons is 157.5 miles.
c) If the car is driven 14,000 miles in one year, the gallons of gasoline used would be 560 gallons.
d) If the gasoline costs $4.10 per gallons, the total cost of purchasing gasoline for the year is $2,296.
e) The miles per gallon is 25 mpg.
f) The gasoline cost per mile is $0.164.
What are miles per gallon?Miles per gallon (MPG) shows the distance traveled by a vehicle, measured in miles, per gallon of gasoline.
The mpg is used to assess a vehicle's fuel efficiency.
a) The volume of the car's gas tank = 17 gallons
The distance on a single tank of gas = 425 miles
Let r = the rate of gasoline consumption per mile
An equation to show the relationship between the number of gallons of gasoline and the distance driven = 425/17 = 25 mpg
b) The number of gallons of gas in the tank = 6.3 gallons
The total distance to be traveled using 6.3 gallons = 157.5 miles (6.3 x 25)
c) If the car is driven 14,000 miles in one year, the gallons of gasoline used would be = 560 gallons (14,000/25).
d) The cost of gasoline per gallon = $4.10
The total cost of purchasing gasoline for the year = $2,296 ($4.10 x 560)
e) The miles per gallon = 25 mpg (14,000/560).
f) The gasoline cost per mile = $0.164 (560 x $4.10)/14,000
Learn more about computing miles per gallon at https://brainly.com/question/16921736.
#SPJ1
Coach Brown buys packs of Gummi Bears at $0. 60 and resales them at $1. 0. At what percent did he mark the candy up?
A. 10. 47
B. 3. 59
C. 9
D. 67
E. 69
F. 10. 25
Answers
If the coach buys the packs of Gummi Bears at $0.60 and resales them at $1 , then the percent markup for the candy is (d) 67% .
The price for which the Coach buys Gummi Bears is = $0.60 ;
the price at which the Coach resales them is = $1 ;
So , the Markup is the difference in the price of purchase and price of resale of the candy ,
that means ; the \(Markup = \$1 - \$0.60\) ;
= $0.4
So , the Percent Markup is = \(\frac{0.4}{0.6} \times 100\)
= 66.66666...
≈ 67% .
Therefore , the percent Markup for the Candy is 67% .
Learn more about Percent Markup here
https://brainly.com/question/29406692
#SPJ4
A flagpole 12 meters tall casts a 24-meter shadow. Nearby, luke stands and is 4 meters tall. Determine the length of luka's shadow. Include all labels.
Answers
Answer:
8 meters
Step-by-step explanation:
This is a question that deals with Proportion
Height of flagpole/Shadow of flagpole = Height of Luke/Shadow of Luke
Length of the shadow of Luke = x
= 12/24 = 4/x
We cross Multiply
12 × x = 24 × 4
x = 24 × 4/12
x = 8 meters
Hence, the length of the shadow of Luke = 8 meters
Review the graph of function f(x).
what are lim x-> 0 f(x) and lim x-> 0 f(x) if they exist

Answers
The two limits when x tends to zero are:
\(\lim_{x \to \ 0^-} f(x) = 1\\\\ \lim_{x \to \ 0^+} f(x) = 0\)
How to get the limits when x tends to zero?Notice that we have a jump at x = 0.
Then we can take two limits, one going from the negative side (where we will go along the blue line)
And other from the positive side (where we go along the orange line).
We will get:
\(\lim_{x \to \ 0^-} f(x) = 1\\\\ \lim_{x \to \ 0^+} f(x) = 0\)
Notice that the two limits are different, that means that the function is not a continuous function.
If you want to learn more about limits:
https://brainly.com/question/5313449
#SPJ1
If your car gets 31 miles per gallon, how much does it cost to drive 440 miles when gasoline costs $3.40 per gallon?
Answers
Answer:
48.3
Step-by-step explanation:
First divide 440 by 31. You get roughly 14.2 so that's how much gallons your gonna need to get to your destination. Multiply 14.2 times 3.40 and you get roughly 48.3 dollars. That's how much your gonna spend.
The graph of a cosine function is shown. Which two points on the midline of the function are separated by a distance of one period?

Answers
Answer: (pi/8, 1) and (5*pi/8, 1)
Step-by-step explanation:
First, the midline is a horizontal line that cuts the graph in two halves.
In this case, we can see that the maximum of the function is y = 2.5, and the minimum is y = -0.5
The difference is:
Diff = (2.5 - (-0.5)) = 3
If we subtract half of the difference (3/2 = 1.5) to the maximum, we get the midline.
Then:
midline: y = 2.5 - (3/2) = 1
the midline is the line y = 1
Now, a period T is such that:
Sin(x) = Sin(x + T)
Two points that are in the midline and that are separated by a period will be two points on the line y = 1, and that are in corresponding parts of the graph.
Here the two points are, counting from left to right, the third and the 11th.
(both of them are in the line y = -1 and in the negative slope part).
The points are:
(pi/8, 1) and (5*pi/8, 1)
Answer:
Here is the correct answer from the other Brainly Answer if you don't know what points you have to mark :) - Edmentum/Plato btw
anyone know what the answer is???(sorry if it’s unclear)

Answers
The laws of exponents I will be using are:
\((x^y)^z = x^{yz}\), and \(x^y \cdot x^z = x^{y+z}\).
For the first part, \((15^3)^3 \cdot 15^{-6} = 15^9 \cdot 15^{-6} = 15^3\).
For the second part, \(15 \cdot (15^3)^2 \cdot (15^{-5})^2 = 15 \cdot (15^6) \cdot (15^{-10}) = 15^{1+6-10} = 15^{-3} = \frac{1}{15^3}\).
PLEASE HURRY
The equation y = 1.6x represents the number of laps Henry can swim over time, where y is the number of laps and x is time in minutes. This table shows the number of laps Larry can swim over time.
How many laps can each boy complete per minute, and who can swim laps at a faster rate?
Select from the drop-down menu to correctly complete the statements.
Henry swims at 11.6 laps per minute and Larry swims at 21.8 laps per minute. Henry swims at a 3slower rate than Larry.

Answers
Henry swims at 1.6 laps per minute and Larry swims at 7 laps per minute. Henry swims at a 5.4 slower rate than Larry.
How to complete the blanks?From the question, we have the following parameters that can be used in our computation:
The equation and the graph
From the equation, we have
Henry: y = 1.6x
Larry: y = 7x
The coefficients of x in the above equations represent their rates
This means that
Henry: = 1.6 laps per minute
Larry:= 7 laps per minute
When the rates are compared, we have
Difference = 7 -1.6
Evaluate
Difference = 5.4
Hence, the values that complete the blanks are 1.6, 7 and 5.4
Read more about rates at
https://brainly.com/question/19493296
#SPJ1
A tubular rod becomes cold in the air. The initial temperature of rod is TO. The temperature and convection coefficient of the air are T. and h... The heat capacity, density and conduction coefficient of the rod are C, p and K. At unsteady condition, find the temperature profile of the rod in r direction, by taking element.
Answers
The temperature profile of the rod in r direction, by taking element.
m * C * (dT/dt) = -K * (dT/dr) + h * (T - \(T_{air}\))
When a tubular rod is exposed to the surrounding air, it tends to lose heat and becomes cold. To analyze the temperature distribution along the rod, we need to consider factors such as the initial temperature of the rod, the temperature and convection coefficient of the air, and the heat capacity, density, and conduction coefficient of the rod itself. In this explanation, we will derive the temperature profile of the rod in the radial (r) direction under unsteady conditions.
To determine the temperature profile of the rod in the radial direction, we'll consider a small element within the rod at a radial distance of r from the center. Let's denote the temperature of this element as T(r, t), where 't' represents time.
According to the laws of heat transfer, the rate at which heat is conducted through this small element is given by Fourier's Law:
\(q_{cond}\) = -K * (dT/dr)
Here, K is the conduction coefficient of the rod, and dT/dr represents the temperature gradient in the radial direction.
Additionally, the rate at which heat is convected from the surface of the rod to the surrounding air is given by Newton's Law of Cooling:
\(q_{conv}\) = h * (T - \(T_{air}\))
Here, h represents the convection coefficient of the air, \(T_{air}\) is the temperature of the air, and (T - \(T_{air}\)) represents the temperature difference between the rod surface and the surrounding air.
Considering the conservation of energy, the change in energy within the small element is equal to the sum of the heat conducted and convected:
dQ = \(q_{cond}\) * dA + \(q_{conv}\) * dA
Here, dA represents the surface area of the small element.
The change in energy within the element can also be expressed as the product of its mass (m), heat capacity (C), and the change in temperature with time (dT/dt):
dQ = m * C * (dT/dt)
By equating these two expressions for dQ, we get:
m * C * (dT/dt) = -K * (dT/dr) * dA + h * (T - \(T_{air}\)) * dA
Since the rod is assumed to have uniform properties, we can simplify the equation by canceling out the surface area (dA) term and rearranging:
m * C * (dT/dt) = -K * (dT/dr) + h * (T - \(T_{air}\))
This is a partial differential equation that describes the temperature distribution within the rod at a given radial distance (r) and time (t). Solving this equation will give us the temperature profile T(r, t) as a function of the radial distance from the rod's center.
To solve this equation, we would need to apply appropriate boundary conditions (such as the initial temperature distribution, TO, at t=0) and possibly additional information regarding the specific properties of the rod and the environment.
To know more about Differential Equation here
https://brainly.com/question/32514740
#SPJ4
a. Find 5
∑
n=0
(9(2) n)−7(−3) n)
b. Given the following premises are p→q,¬p→r, and r→s. Prove that ¬q→s
c. Show that ¬(p∨¬q) and q∧¬p are equivalent by:
Answers
By using the same logic and identity, we can also say that ¬(p∨¬q) is equivalent to q∧¬p.
a. To find the given series i.e., 5∑n=0(9(2)n)−7(−3)nTo find 5∑n=0(9(2)n)−7(−3)n,
we need to find the first five terms of the series. The given series is,
5∑n=0(9(2)n)−7(−3)n5[(9(2)0)−7(−3)0] + [(9(2)1)−7(−3)1] + [(9(2)2)−7(−3)2] + [(9(2)3)−7(−3)3] + [(9(2)4)−7(−3)4]
After evaluating, we get:
5[(9*1) - 7*1] + [(9*2) - 7*(-3)] + [(9*4) - 7*9] + [(9*8) - 7*(-27)] + [(9*16) - 7*81]15 + 57 + 263 + 1089 + 4131= 5555b.
Given premises: p → q, ¬p → r, r → s.
We are to prove that ¬q → s. i.e.,
Premises: (p → q), (¬p → r), (r → s)
Conclusion: ¬q → s
To prove ¬q → s,
we need to assume ¬q and show that s follows.
Then we use the premises to derive s.
Proof:
1. ¬q Assumption
2. ¬(¬q) Double negation
3. p Modus tollens 2,1 & p → q
4. ¬¬p Double negation
5. ¬p Modus ponens 4,3 (Conditional elimination)
6. r Modus ponens 5,2 (Conditional elimination)
7. s Modus ponens 6,3 (Conditional elimination)
8. ¬q → s Conditional introduction (Implication)
Thus, ¬q → s is proven.
c. To show that ¬(p∨¬q) and q∧¬p are equivalent, we need to show that their negation is equivalent. i.e.,
we show that (p ∨ ¬q) ↔ ¬(q ∧ ¬p)Negation of (p ∨ ¬q) = ¬p ∧ q Negation of (q ∧ ¬p) = ¬q ∨ p
Thus, we are to show that (p ∨ ¬q) ↔ ¬(q ∧ ¬p) is equivalent to ¬p ∧ q ↔ ¬q ∨ p
Proof:
¬(q ∧ ¬p) ≡ ¬q ∨ p Negation of (q ∧ ¬p)(p ∨ ¬q) ≡ ¬(q ∧ ¬p)
De Morgan's laws ∴ (p ∨ ¬q) ≡ ¬q ∨ p
By using the same logic and identity, we can also say that ¬(p∨¬q) is equivalent to q∧¬p.
To know more about equivalent visit:
https://brainly.com/question/24207766
#SPJ11
a. The formula given is, ∑n=0(9(2)n)−7(−3)n. Let’s find out the first five terms of the given formula as follows:
First term at n = \(0:9(2)^0-7(-3)^0= 9 + 7= 16\)
Second term at n = \(1:9(2)^1-7(-3)^1= 18 + 21= 39\)
Third term at n = \(2:9(2)^2-7(-3)^2= 36 + 63= 99\)
Fourth term at n = \(3:9(2)^3-7(-3)^3= 72 + 189= 261\)
Fifth term at n = \(4:9(2)^4-7(-3)^4= 144 + 567= 711\)
Therefore, the first five terms of the given formula are: 16, 39, 99, 261, 711.
b. To prove that ¬q→s from p→q, ¬p→r, and r→s,
we need to use the law of contrapositive for p→q as follows:
¬q→¬p (Contrapositive of p→q)¬p→r (Given)
∴ ¬q→r (Using transitivity of implication) r→s (Given)
∴ ¬q→s (Using transitivity of implication)
Therefore, ¬q→s is proved.
c. To show that ¬(p∨¬q) and q∧¬p are equivalent,
we need to use the De Morgan’s laws as follows:
¬(p∨¬q) ≡ ¬p∧q (Using De Morgan’s law)
≡ q∧¬p (Commutative property of ∧)
Therefore, ¬(p∨¬q) and q∧¬p are equivalent.
To know more about law of contrapositive visit:
https://brainly.com/question/17831746
#SPJ11
The amounts below show the change (measured in feet) in water
level over four months. What is the average monthly change in
water level?
-2.54, -3.16, -2.82, 1.6
Answers
Answer: -1.73 ft
Step-by-step explanation:
(-2.54 - 3.16 - 2.82 + 1.6) / 4 = -1.73
Two points are g phedo the comdinate plane.
2
-1
-6
-5
-4
-3
-2
1
2
>
4
1 a
-1
S
6
7
-2
-3
A А
4
--5
-6
-7 기
-8
9
B
-10)
What is the distance between the two points? Enter the answer in the box
units
< Previous
Answers
Answer:
b
Step-by-step explanation:
yp
Answer:
huh
Step-by-step explanation:

