PLEASEEEEE HELP! Drag the numbers to the correct locations in the equation. Each number can be used more than once, but not all numbers will be used. The average commute time, in minutes, in relation to the population, in millions, of 10 major cities is shown in the table. What is the square root equation that best models this set of data?

Answers
9514 1404 393
Answer:
\(y=10.9\sqrt{x-0.5}+23.7\)
Step-by-step explanation:
A graphing calculator or spreadsheet can help you do the square root regression. See the attachment for the result.
\(y=10.9\sqrt{x-0.5}+23.7\)

Answer:
see image
Step-by-step explanation:
Plato/Edmentum

Related Questions
what is the answer for -2.3 - 5 = x - 17
Answers
Answer:
Step-by-step explanation:
If you are solving x then do this:
-2.3-5=x-17
First combine like term.
-7.3=x-17
Then add each side of the equation by 17 (we aren't subtracting because we are trying to get rid of -17 so to get rid of it we add by 17).
-7.3 +17 = x-17+17
9.7=x
A father wants to gift his daughter a present for her marriage, he offers her three options Option A $56.000 today Option $4.000 every year for 10 years Option C $90,000 in 10 years Assuming a discount rate of 7%, calculate the present value of each option (give an answer for each) and decide what option is best for the daughter
Answers
The present values of the options for the father to gift his daughter would be:
Option A = $ 56, 000Option B = $ 28, 094.40Option C = $ 45, 758. 72How to find the present values ?The present value is simply $ 56, 000 because it's given today.
Option B is an annuity so the present value would be:
PV = Pmt x [ 1 - ( 1 + r ) ⁻ ⁿ ] / r
= 4, 000 x ( 1 - ( 1 + 7 % ) ⁻ ¹⁰ ) / 0. 07
= $ 28, 094. 40
Option C 's present value would be:
= Future value / ( 1 + rate ) ⁿ
= 90, 000 / ( 1 + 7 % ) ¹⁰
= $ 45, 758.72
Find out more on present value at https://brainly.com/question/31378011
#SPJ1
Find the real part of the particular solution Find the real part of the particular solution to the differential equation 2dt2d2y+2dtdy+8y=e4it in the form y=Bcos(4t)+Csin(4t) where B,C are real fractions. Re(
Answers
The real part of the particular solution is (-1/20)cos(4t).
How to find the real part?
General solution:2d^2y/dt^2 + 2dy/dt + 8y = 0
The characteristic equation is:2r^2 + 2r + 8 = 0
Solving for r using the quadratic formula, we get:r = (-2 ± √(2^2 - 4(2)(8))) / (2(2))
r = -1/2 ± i
The general solution of the homogeneous equation is:y_h = e^(-t/2)(C1 cos(t/2) + C2 sin(t/2))
To find the particular solution, we assume :y_p = A cos(4t) + B sin(4t)
Taking the first and second derivatives of y_p, we get:d^2y_p/dt^2 = -16A cos(4t) - 16B sin(4t)
Substituting y_p and its derivatives into the differential equation, we get:(-16A cos(4t) - 16B sin(4t)) + 2(-4A sin(4t) + 4B cos(4t)) + 8(A cos(4t) + B sin(4t)) = e^(4it)
Simplifying(-16A + 8B + 8)e^(4it) + (-16B - 8A)sin(4t) + (8B - 16A)cos(4t) = 0
-16B - 8A = 0
8B - 16A = 1
A = -1/20
B = -1/40
y_p = (-1/20)cos(4t) - (1/40)sin(4t)
The real part of the particular solution:Re(y_p) = (-1/20)cos(4t)
Learn more about real part
brainly.com/question/13389642
#SPJ11
An indoor trampoline park has an admission fee, plus an hourly charge. The graph displays the total cost from 3, 4, 5, and 6 hours of play. Determine the hourly change, assuming the relationship is linear.
Rate of Change=$ per hour
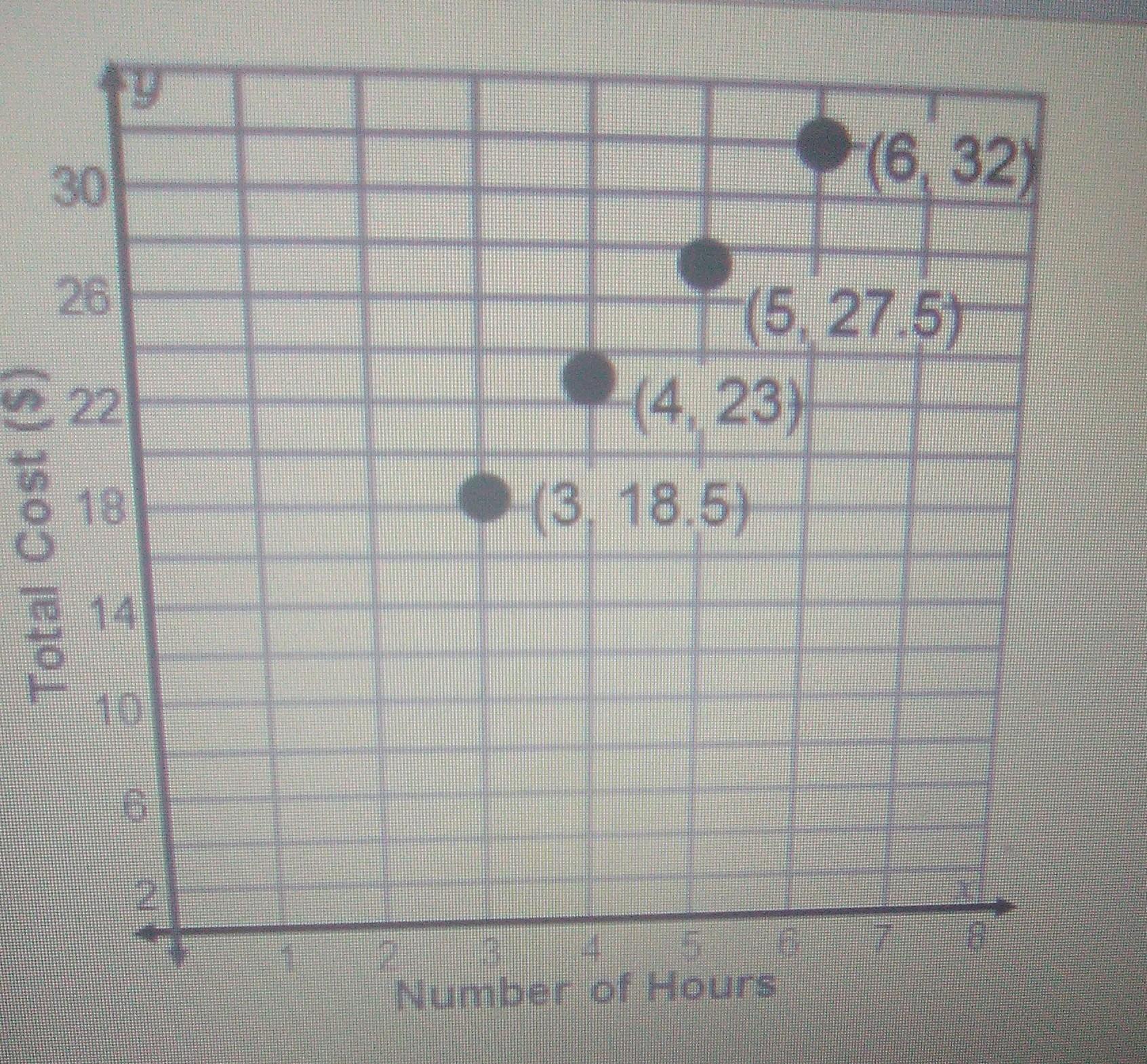
Answers
Answer:
$4.5 per hour
Step-by-step explanation:
Hope this was accurate and help full. I hope you have a lovely day!
Answer:
4.5
Step-by-step explanation:
HELP PLEASE I WILL MARK BRAINOEST

Answers
Answer:
y ≤ 1/3x - 4
Step-by-step explanation:
it could not be options 3 or 4 because the y-intercept is -4, not +4
I picked a point in the shaded area to see which inequality, the first or the second, would make it true; the point I used was (3, -4)
1st option: y ≥ 1/3x - 4 Is this true? -4 ≥ 1/3(3) No, -4 is not GE 1
2nd option: y ≤ 1/3x - 4 Is this true? -4 ≤ 1/3(3) Yes, -4 is LE 1
Is `(2,5)` a solution to the system:
`x+y=7`
`2x-3y=-11`
Answers
Answer:
the answer is in the picture.. if you need to actually solve the system please tell me and i will send that too

how many coorinates are on a coordinate plane?
A. 1
B. 6
C. 4
Answers
Answer:
4
Step-by-step explanation:
if you're talking about quadrants on a coordinate plane then it is 4:)
coordinate planes are separated into four quadrants (qI,qII,qIII,qIV) shaped like a plus sign, 2 positive quadrants and 2 negative.
Answer:
4! They are called quadrants and quad means 4 <3
Step-by-step explanation:
Evaluate the function f(x)=2x-7 using the values given below. f(-3)=
Answers
Answer:
-13
Step-by-step explanation:
f(x)=2x-7
f(-3)=2(-3)-7=-6-7=-13
5x + 2y = 7
7x + 6y = -3
Please solve using elimination method.
Answers
hope that helps
A bank advertises a 2/1 arm at 2.75% with a 2/10 cap. what is the maximum interest rate that can be charged during the fifth year? a. 2.75% b. 4.75% 6c. 75% d. 8.75%
Answers
The maximum interest rate that can be charged during the fifth year is 6.75%. The correct option is the third option c. 6.75%
Calculating the maximum interest rate that can be chargedFrom the question, we are to determine the maximum interest rate that can be charged during the fifth year
A 2/1 ARM means that the interest rate is fixed for the first two years and then adjusts annually based on a specified index plus a margin. The "2/10 cap" means that the interest rate can only increase or decrease by a maximum of 2 percentage points each year, and can never be more than 10 percentage points higher than the initial rate.
Since the initial rate is 2.75%, the maximum rate that can be charged during the fifth year is:
2.75% + (2 x 2%) = 6.75%
Hence, the maximum interest rate that can be charged during the fifth year is 6.75%.
Learn more on Calculating the maximum interest rate that can be charged here: https://brainly.com/question/2668857#:~:text=Expert%2DVerified%20Answer&text=M%20people%20helped-,The%20maximum%20interest%20rate%20that%20can%20be,the%20fifth%20year%20is%2011.15%25.
#SPJ1
why is math the best subject?
Answers
Answer:
math is the most annoying
subject known to men
Step-by-step explanation:
Answer:
its not :)
Step-by-step explanation:
3. Find the value of r so the line that passes through (7,r) & (1, -1), has a slope ofm=į (9 pts)Hi can Someone please help !
Answers
You have the following points:
(7,r)
(1,-1)
and you have to find the value of r, that makes that the line which crosses the previous points has a slope of m = 1/2.
To find the value of r, you use the following formula for the slope m:
m = (y2 - y1)/(x2 - x1)
where (x1,y1) and (x2,y2) are two point of the line.
The points are:
(x1,y1) => (1,-1)
(x2,y2) => (7,r)
replace the previous values in the formula for the slope m, and solve for r:
m = (r - (-1))/(7 - 1)
m = (r + 1)/(6) multiply both sides by 6
6m = r + 1 subtract both sides by 1
6m - 1 = r replace the value of m = 1/2
6(1/2) - 1 = r
3 - 1 = r
2 = r
Hence, the value of r has to be r = 2 for getting a slope of m = 1/2 of a line which crosses the given points
how do you solve x - 2y = 10; for y
Answers
Answer:
Y=5
Step-by-step explanation:
Help asap!!!!
Around which line would the following cross-section need to be revolved to create a sphere?
circle on a coordinate plane with center at 1 on the x-axis and a radius of 1
y = x
y-axis
x = 1
y = 1
Answers
Answer:
I believe your answer would be y=1.
Step-by-step explanation:
The circle is located with its point on 1 of the x axis, and the cross section would be pulled straight from that term. So the cross section would need to be revolved around y = 1, instead.
This is just my best guess, so I hope it helps!
To get a sphere, we need to do a revolution around the line x = 1.
Which line should we use?
The line that we must use must be a line that divides the circle in two equal parts, so it must pass through its center.
We know that the center of our circle is the point (1, 0).
With that in mind, the two lines that we know that will divide the circle in two equal parts are:
y = 0x = 1(There are more lines, the above two are the simplest ones).
The only one that appears on the options is x = 1, so that is the correct option.
If you want to learn more about circles, you can read:
https://brainly.com/question/25306774
(Finding constants) For functions f(n)=0.1n 6
−n 3
and g(n)=1000n 2
+500, show that either f(n)=O(g(n)) or g(n)=O(f(n)) by finding specific constants c and n 0
for the following definition of Big-Oh: Definition 1 For two functions h,k:N→R, we say h(n)=O(k(n)) if there exist constants c>0 and n 0
>0 such that 0≤h(n)≤c⋅k(n) for all n≥n 0
Answers
Either f(n)=O(g(n)) or g(n)=O(f(n)) since f(n) can be bounded above by g(n) with suitable constants.
To show that either f(n) = O(g(n)) or g(n) = O(f(n)), we need to find specific constants c > 0 and n_0 > 0 such that 0 ≤ f(n) ≤ c * g(n) or 0 ≤ g(n) ≤ c * f(n) for all n ≥ n_0.
Let's start by considering f(n) = 0.1n^6 - n^3 and g(n) = 1000n^2 + 500.
To show that f(n) = O(g(n)), we need to find constants c > 0 and n_0 > 0 such that 0 ≤ f(n) ≤ c * g(n) for all n ≥ n_0.
Let's choose c = 1 and n_0 = 1.
For n ≥ 1, we have:
f(n) = 0.1n^6 - n^3
≤ 0.1n^6 + n^3 (since -n^3 ≤ 0.1n^6 for n ≥ 1)
≤ 0.1n^6 + n^6 (since n^3 ≤ n^6 for n ≥ 1)
≤ 1.1n^6 (since 0.1n^6 + n^6 = 1.1n^6)
Therefore, we have shown that for c = 1 and n_0 = 1, 0 ≤ f(n) ≤ c * g(n) for all n ≥ n_0. Hence, f(n) = O(g(n)).
Similarly, to show that g(n) = O(f(n)), we need to find constants c > 0 and n_0 > 0 such that 0 ≤ g(n) ≤ c * f(n) for all n ≥ n_0.
Let's choose c = 1 and n_0 = 1.
For n ≥ 1, we have:
g(n) = 1000n^2 + 500
≤ 1000n^6 + 500 (since n^2 ≤ n^6 for n ≥ 1)
≤ 1001n^6 (since 1000n^6 + 500 = 1001n^6)
Therefore, we have shown that for c = 1 and n_0 = 1, 0 ≤ g(n) ≤ c * f(n) for all n ≥ n_0. Hence, g(n) = O(f(n)).
Hence, we have shown that either f(n) = O(g(n)) or g(n) = O(f(n)).
Learn more about bounded above here
https://brainly.com/question/28819099
#SPJ11
Which of the binomials below is a factor of this
trinomial?
x2 - 13x + 30
O A. X-3
O B. X+5
O c. x-5
O D. X+ 3
Answers
Answer:
A
Step-by-step explanation:
Given
x² - 13x + 30
Consider the factors of the constant term (+ 30) which sum to give the coefficient of the x- term (- 13)
The factors are - 3 and - 10, since
- 3 × - 10 = + 30 and - 3 - 10 = - 13 , thus
x² - 13x + 30 = (x - 3)(x - 10) ← in factored form
Thus (x - 3) is a factor of the polynomial → A
Answer:
\((x - 3)\)
Answer A is correct
Step-by-step explanation:
\({x}^{2} - 13x + 30 \\ {x}^{2} - 10x - 3x + 30 \\ x(x - 10) - 3(x - 10) \\ = (x - 3)(x - 10)
\\ \)
hope this helps
brainliest appreciated
good luck! have a nice day!
Write an algebraic expression that you can use to determine the total cost of buying a watermelon that weighs w pounds and some tomatoes that weigh t pounds. Watermelons are on sale for $0.68 per lb and tomatoes are $3.25 per lb. (Do not enter dollar signs or spaces in your expression.)
Answers
Answer:
C = 0.68w + 3.25t
C is total cost
Step-by-step explanation:
Need help with the following Questions
How would you calculate the distance in miles between two people on the same line of latitude? First, sum to the total distance between the points in degrees, then multiply that sum by the statute miles per degree for the shared line of latitude. (Hint: Sometimes it is easier to visualize this by plotting it on a graph).
A. How many miles are between the following two locations: 60°N, 30°W & 60°N 50°E
B. How many miles are between the following two locations: 30°S, 60°W & 30°S 90°E
Answers
The distance between two locations on the same line of latitude can be calculated by summing the total distance between the points in degrees and multiplying it by the statute miles per degree for the shared line of latitude.
To calculate the distance in miles between two locations on the same line of latitude, we first need to find the total distance between the points in degrees. In the case of location A, which is 60°N, 30°W, and location B, which is 60°N, 50°E, the total distance between the two points is 80 degrees (50°E - 30°W).
Next, we need to multiply the sum of the degrees by the statute miles per degree for the shared line of latitude. Since the line of latitude is 60°N, we need to determine the statute miles per degree at that latitude.
The Earth's circumference at the equator is approximately 24,901 miles, and since a circle is divided into 360 degrees, the distance per degree at the equator is approximately 69.17 miles (24,901 miles / 360 degrees).
Multiplying the total distance in degrees (80 degrees) by the statute miles per degree (69.17 miles), we find that the distance between the two locations is approximately 5,533.6 miles.
Similarly, for location C, which is 30°S, 60°W, and location D, which is 30°S, 90°E, the total distance between the points is 150 degrees (90°E - 60°W). Since the line of latitude is 30°S, we use the same statute miles per degree value (69.17 miles).
Multiplying the total distance in degrees (150 degrees) by the statute miles per degree (69.17 miles), we find that the distance between the two locations is approximately 10,375.5 miles.
Therefore, the distance between locations A and B is approximately 5,533.6 miles, and the distance between locations C and D is approximately 10,375.5 miles, when calculated using the given method.
Learn more about circumference here:
https://brainly.com/question/28757341
#SPJ11
Can someone help me write a proof for this problem

Answers
The solution is, the triangle ABC and DBC are congruent, by the Side-Angle-Side Triangle Congruence Theorem.
What is triangle?A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane.
here, we have,
As we can seen from the given figure that two triangles are given.
The triangles ABC and BDC are :
AB = CD
AC = BD
BC = BC
Hence using the SSS theorem of the triangle, the triangle ABC and DBC are congruent, Thus the angle A is equal to angle D.
Hence the option D and E are correct. i.e. congruent by the Side-Angle-Side Triangle Congruence Theorem.
Learn more about the statements that are true about the triangles.
brainly.com/question/25258416.
#SPJ1
-85<5h-8+2h solve for h
Answers
Answer:
h > -11
Step-by-step explanation:
Given the inequality expression, -85 < 5h - 8 + 2h:
The goal is to isolate the variable in order to solve for h.
Start by adding 8 to both sides and combine like terms:
-85 + 8 < 5h - 8 + 8 + 2h
-77 < 7h
Divide both sides by 7 to isolate h:
\(\frac{-77}{7} < \frac{7h}{7}\)
-11 < h or h > -11.
Answer:
h < -11
Step-by-step explanation:
-85 < 5h - 8 + 2h
First, we combine like terms:
-85 < 7h - 8
Next, we reorder the equation to make it easier for the next step.
7h - 8 < -85
Now, to isolate 7h, we transpose -8 to the other side of the less than sign.
Always remember that when we transpose something, wheter it's a number or variable, you must always switch it from negative to positive or positive to negative.
-8 is negative, so when it crosses the less-than sign, it turns into a +8.
So we do:
7h < -85 + 8
We combine like terms:
7h < -77
Now we simplify:
h < -11
Therefore, h < -11 in the equation -85 < 5h - 8 + 2h.
ʜᴏᴘᴇ ᴛʜɪꜱ ʜᴇʟᴘᴇᴅ!
ʜᴀᴠᴇ ᴀ ɴɪᴄᴇ ᴅᴀʏ!
In a class full of men and women, 2 /9 of the class are women. What is the ratio of men to women in its simplest form?
Answers
Answer:
7:2
Step-by-step explanation:
2/9= women
9/9= total of men and women
7/9= men
men to women (use the numerators)
7:2
Answer:
7:2
Step-by-step explanation:
2/9 are women.
1 - 2/9 = 7/9
7/9 are men.
Put up a ratio of men to women.
7/9 : 2/9
Simplify.
63:18
7:2
You are asked to solve 9x = 3x + 84. Which three statements are true? es ) A) B) Subtract 3x from both sides. x = 14 E x = 6
Answers
Answer:
What? in this equation, x = 14. I'm not sure what the question is asking.
what is 3(x−1)−(2x+4) hurryyyy!!!!!!!
Answers
Answer:
x-7
Step-by-step explanation:
3(x-1)-(2x+4)
3x-3-2x-4
3x-2x-3-4
x-3-4
x-7
The function below represents the position f in feet of a particle at time x in seconds. find the average height of the particle on the given interval
f(x) = 3x^2 + 6x, [-1, 5]
Answers
Therefore, the average height of the particle on the interval [-1, 5] is approximately 33.67 feet.
To find the average height of the particle on the interval [-1, 5], we need to evaluate the definite integral of the position function f(x) = 3x^2 + 6x over that interval and divide it by the length of the interval.
The average height (H_avg) is calculated as follows:
H_avg = (1 / (b - a)) * ∫[a to b] f(x) dx
In this case, a = -1 and b = 5, so the average height is:
H_avg = (1 / (5 - (-1))) * ∫[-1 to 5] (3x^2 + 6x) dx
To evaluate the integral, we can use the power rule of integration:
∫ x^n dx = (1 / (n + 1)) * x^(n+1) + C
Applying this rule to each term in the integrand, we get:
H_avg = (1 / 6) * [x^3 + 3x^2] evaluated from -1 to 5
Now, we can substitute the limits of integration into the expression:
H_avg = (1 / 6) * [(5^3 + 3(5^2)) - ((-1)^3 + 3((-1)^2))]
H_avg = (1 / 6) * [(125 + 75) - (-1 + 3)]
H_avg = (1 / 6) * [200 - (-2)]
H_avg = (1 / 6) * 202
H_avg = 33.67 feet
To know more about interval,
https://brainly.com/question/1619430
#SPJ11
A real estate broker earns a fixed percentage of the selling price of a house as a commission. The broker sold a house for $ 278,000 and earned a commission of $ 16,680. What would the broker's commission be on a house that sells for $ 324,000?
Answers
first, we find the percentage of the commission earned:
$278,000 ----> 100%
$16,680 ------> x
then solve
\(\begin{gathered} 278000\cdot x=16680\cdot100 \\ 278000x=1668000 \\ \frac{278000x}{278000}=\frac{1668000}{278000} \\ x=6 \end{gathered}\)therefore the commission is 6%. So,
$324,000 ------> 100%
y -------------------> 6%
\(\begin{gathered} y\cdot100=324000\cdot6 \\ 100y=1944000 \\ \frac{100y}{100}=\frac{1944000}{100} \\ y=19440 \end{gathered}\)answer: $ 19,440
the correct fumber of significant digiss
Answers
The correct number of significant digits in a measurement depends on the precision of the measuring instrument and the certainty of the measurement.
The number of significant digits in a measurement indicates the precision and accuracy of the measurement. Significant digits are the digits that carry meaning and contribute to the overall precision of the measurement. The rules for determining the correct number of significant digits are as follows:
1. Non-zero digits are always significant. For example, in the number 123.45, all the digits (1, 2, 3, 4, and 5) are significant.
2. Zeroes between non-zero digits are also significant. For example, in the number 1.003, all the digits (1, 0, 0, and 3) are significant.
3. Leading zeroes (zeros to the left of the first non-zero digit) are not significant. For example, in the number 0.0056, the significant digits are 5 and 6.
4. Trailing zeroes (zeros to the right of the last non-zero digit) are significant if they are after a decimal point or if they have been measured. For example, in the number 1.00, all the digits (1, 0, 0) are significant.
It is important to report the correct number of significant digits in a measurement to convey the precision and accuracy of the data. Failing to do so may result in misleading or incorrect interpretations of the results.
Learn more about significant digits here:
https://brainly.com/question/28993414
#SPJ11
The complete question is:
How do you determine the correct number of significant digits?
Write tan 41π/36 in terms of the tangent of a positive acute angle.
Answers
tan(41π/36) can be written in terms of the tangent of a positive acute angle as (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
To express tan(41π/36) in terms of the tangent of a positive acute angle, we need to find an angle within the range of 0 to π/2 that has the same tangent value.
First, let's simplify 41π/36 to its equivalent angle within one full revolution (2π):
41π/36 = 40π/36 + π/36 = (10/9)π + (1/36)π
Now, we can rewrite the angle as:
tan(41π/36) = tan((10/9)π + (1/36)π)
Next, we'll use the tangent addition formula, which states that:
tan(A + B) = (tan(A) + tan(B)) / (1 - tan(A)tan(B))
In this case, A = (10/9)π and B = (1/36)π.
tan(41π/36) = tan((10/9)π + (1/36)π) = (tan((10/9)π) + tan((1/36)π)) / (1 - tan((10/9)π)tan((1/36)π))
Now, we need to find the tangent values of (10/9)π and (1/36)π. Since tangent has a periodicity of π, we can subtract or add multiples of π to get equivalent angles within the range of 0 to π/2.
For (10/9)π, we can subtract π to get an equivalent angle within the range:
(10/9)π - π = (1/9)π
Similarly, for (1/36)π, we can add π to get an equivalent angle:
(1/36)π + π = (37/36)π
Now, we can rewrite the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Since we are looking for an angle within the range of 0 to π/2, we can further simplify the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Therefore, tan(41π/36) can be written in terms of the tangent of a positive acute angle as the expression given above.
For more about tangent:
https://brainly.com/question/19064965
#SPJ4
The triangles are similar. what is the value of x? enter your answer in the box. x = two right triangles. the larger triangle has a long leg of 36 units, a short leg of 15 units, and a hypotenuse of 39 units. the smaller triangle has a long leg of 12 units, short leg of 5 units, and the hypotenuse is labeled x minus 10.
Answers
For the above set of similar triangles, the value of x is 23 units.
What is similar triangles?Similar triangles have the same proportionate side lengths and related angle measurements. Two triangles are comparable if their corresponding angles and sides have the same ratio (or proportion). Similar triangles will have the same form but may or may not have the same size. Similar triangles are triangles that have the same shape but differ in size. Similar items include all equilateral triangles and squares with any side length. In other words, if two triangles are identical, their corresponding angles and sides are congruent and in equal proportion.
Here,
Two triangles are comparable if their corresponding angles and sides have the same ratio (or proportion).
x-10/39=12/36
x-10=13
x=23
The value of x for given set of similar triangles is 23 units.
To know more about similar triangles,
https://brainly.com/question/14926756
#SPJ4
PLZ HELP BRAINLIEST if right!!!!

Answers
Answer:
16.2
Step-by-step explanation:
The x is 6.6.
2x+3 = DE
2(6.6)+3
13.2+3
16.2
Hope this helps!
brainliest for help plss
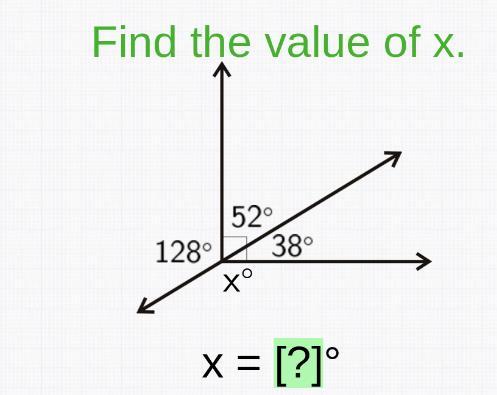
Answers
The value of x , given the angle and the lines drawn , would be 142 degrees .
How to find x angle ?The fact that a straight line was drawn such that x degrees and 38 degrees make up the angles of that line , means that the total angular measure would be 180 degrees because this is the angle of a straight line.
This therefore means that to find the value of x, the formula would be :
x = 180 - 38
x = 180 - 38
x = 142 degrees
In conclusion, the value of x would be 142 degrees.
Find out more on angles at https://brainly.com/question/23925137
#SPJ1