Answers
Answer:
4 kilometers per gallon
Step-by-step explanation:
for unit rate you divided distance by in this case
Related Questions
Rounding factors to their greatest place results in this
Answers
Answer:
I think a polynomial... could be wrong though....
Step-by-step explanation:
Find all the roots of the given function on the given interval. Use pre-liminary analysis and graphing to find good initial approximations.
f(x) = cos (4x) - 4x2 + 9x
Answers
Answer:
The roots for \(f(x) = \cos 4x - 4\cdot x^{2} + 9\cdot x\) are \(x_{1} = -0.098\) and \(x_{2} = 2.166\), respectively.
Step-by-step explanation:
A root is a value of \(x\) so that \(f(x) = 0\). Let suppose that function is the consequence of the subtraction between two functions, that is:
\(f(x) = g(x) - h(x)\) (1)
If we know that \(f(x) = 0\), \(g(x) = \cos 4 x\) and \(h(x) = 4\cdot x^{2}-9\cdot x\), then we have the following identity:
\(g(x) = h(x)\)
We can estimate graphically the roots of \(f(x)\) by graphing the following system:
\(y = \cos 4x\) (2)
\(y = 4\cdot x^{2}-9\cdot x\) (3)
Where roots are the points in which functions find each other.
With the help of a graphing, we estimate two solutions:
\((x_{1}, y_{1}) = (-0.098, 0.924)\), \((x_{2}, y_{2}) = (2.166, -0.725)\)

I'll give brainliest to the right answer!!!
Find three consecutive odd integers such that the difference of twice the second and the first is 11.
Answers
Answer:
7, 9, 11
Step-by-step explanation:
question: Find three consecutive odd integers such that the difference of twice the second and the first is 11.
make the 3 consecutive odd intergers x, y, and z.
numbers are consective (come right after another) AND odd, meaning you would add 2 every time. therefore:
x+2=y
y+2=z
given that: "difference of twice the second and the first is 11."
difference means subtraction
second number is the variable y
first number is the variable x
2y-x=11
----------------
3 equations:
2y-x=11
x+2=y
y+2=z
----------solve by substitution
x+2=y
x =y-2 into 2y-x=11
2y-(y-2)=11
2y-y+2=11
y=9
second number is 9
-----
numbers are 7, 9, 11

According to the CDC, only 20% of Americans get enough exercise each week. You conduct a survey of 200 people.
a. What is the probability that 45 or more people in your survey get enough exercise? Use a normal approximation for p hat
b. Find the exact binomial probability that 45 or more people in your survey get enough exercise.
Answers
The exact binomial probability that 45 or more people in the survey get enough exercise is 0.0853.
What is mean?The mean (also called the arithmetic mean or average) is a measure of central tendency that represents the typical or average value of a set of data. The mean is calculated by summing up all the values in the data set and dividing by the number of values.
According to question:a. To calculate the probability that 45 or more people in the survey get enough exercise using a normal approximation for p hat, we need to first find the mean and standard deviation of the sample proportion.
The mean of the sample proportion is:
μ = p = 0.20
The sample proportion's standard deviation is:
σ = √[(p(1-p))/n] = √[(0.20)(0.80)/200] = 0.034
Using the normal distribution with a continuity correction, we can find the probability of 45 or more people getting enough exercise:
z = (45 - 0.20200 + 0.5) / √(0.200.80*200) = 1.24
P(Z > 1.24) = 0.1082
Therefore, the probability that 45 or more people in the survey get enough exercise is approximately 0.1082.
b. To find the exact binomial probability that 45 or more people in the survey get enough exercise, we can use the binomial cumulative distribution function (CDF) with n = 200 and p = 0.20:
P(X ≥ 45) = 1 - P(X < 45) = 1 - binomcdf(200, 0.20, 44) = 0.0853
Therefore, the exact binomial probability that 45 or more people in the survey get enough exercise is 0.0853.
To know more about mean visit:
https://brainly.com/question/23631778
#SPJ1
a triangular field has boundaries of lengths 170m,195m and 210m,find the size of the largest interior angle of the field
Answers
The size of the largest interior angle of the field is 69.86°
What is cosine law?The law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.
Given that, a triangular field has boundaries of lengths 170m, 195m and 210m, we need to find the size of the largest interior angle of the field,
We know that, angle opposite to the largest side is largest,
Therefore,
The largest angle is opposite is 210 m side, (say c)
Using the cosine rule,
210² = 170²+195²-2(170)(195)cosC
CosC = 170²+195²-210² / 2(170)(195)
CosC = 22825 / 66300
CosC = 0.344268477
C = 69.86°
Hence, the size of the largest interior angle of the field is 69.86°
Learn more about cosine rule, click;
https://brainly.com/question/26952873
#SPJ9
Given the function f(x)=x^2+4x-2. determine the average rate of change of the function over the interval -8<=x<=3
Answers
The average rate of change of the function f(x) = x² + 4x - 2 over the interval [-8,3] is -1.
What is the average rate of change of the function?Given the function in the question;
f(x) = x² + 4x - 2
Interval -8 ≤ x ≤ 3
To find the average rate of change of the function f(x) = x² + 4x - 2 over the interval [-8,3],
we can use the following formula:
average rate of change = \(\frac{f(b) - f(a)}{b - a}\)
Where a and b are the endpoints of the interval.
Substituting the values of a = -8 and b = 3 into the formula, we get:
average rate of change = \(\frac{f(3) - f(-8)}{3 - (-8)}\)
We can now find the values of f(3) and f(-8) using the formula for f(x):
f(x) = x² + 4x - 2
f(3) = (3)² + 4(3) - 2
f(3) = 9 + 12 - 2
f(19) = 19
f(x) = x² + 4x - 2
f(-8) = (-8)² + 4(-8) - 2
f(-8) = 64 -32 - 2
f(-8) = 64 -34
f(-8) = 30
Hence:
average rate of change = \(\frac{f(3) - f(-8)}{3 - (-8)}\)
\(=\frac{19 - 30}{3 - (-8)}\\\\=\frac{-11}{11}\\\\= -1\)
Therefore, the average rate of change is -1.
Learn more about average rate of change here: https://brainly.com/question/13235160
#SPJ1
Fill in the following blank so that the resulting statement is true.
Points: 0 of 1
In order to construct a Venn diagram for a survey, first enter the cardinality of the
to obtain subsequent cardinalities.
Save
region. Then use
Answers
In order to construct a Venn diagram for a survey, first enter the cardinality of the universal set to obtain subsequent cardinalities.
How to explain the informationThe universal set is the set of all possible outcomes, and the cardinality of a set is the number of elements in the set. Once you have the cardinality of the universal set, you can use it to calculate the cardinality of any other set in the survey.
For example, if the universal set has a cardinality of 100, and the survey asks people whether they like dogs or cats, you can calculate the number of people who like dogs by subtracting the number of people who like cats from the total number of people surveyed.
In order to construct a Venn diagram, you will need to draw two or more circles, each representing a set in the survey. The circles should be overlapping to represent the sets that have members in common.
Learn more about Venn diagram on
https://brainly.com/question/24713052
#SPJ1
In order to construct a Venn diagram for a survey, first enter the cardinality of the to obtain subsequent cardinalities region. Then use
The volume of a cuboid is 540cm³. The length is 6cm and the width is 150mm. Work out the height of the cuboid in cm.
Answers
Step-by-step explanation:
To work out the height of the cuboid, we need to use the formula:
Volume = Length x Width x Height
We have been given the volume and the length, so we can substitute those values into the formula:
540 = 6 x Width x Height
Now we need to convert the width from millimeters to centimeters, so we divide it by 10:
150mm ÷ 10 = 15cm
Substituting this value into the formula:
540 = 6 x 15 x Height
Simplifying:
540 = 90 x Height
Dividing both sides by 90:
6 = Height
Therefore, the height of the cuboid is 6cm.
Shanice uses the rule" Divide the number of lawns by 2" to find the gallons of gas needed to run her lawn mower. If 2 gallons of gas are needed for 4 lawns and 4gallons of gas are needed for 8 lawns, how many gallons of gas are needed for 14 lawns?
Answers
Using the concept of ratio and proportions, Shanice will need 7 gallon for 14 lawns.
What is ProportionsProportion is a mathematical concept that describes the relationship between two or more related quantities. It is usually expressed as a ratio or a fraction, which indicates how much of one quantity there is compared to the other. Proportions are used in many areas of mathematics and science, including statistics, geometry, and physics.
In this problem, we have to find the ratio or proportion to which she uses fuel per lawn.
2 gallons = 4 lawns
1 gallon = x lawn
x = (4 * 1) / 2
x = 4 / 2
x = 2 lawn
So, she uses 1 gallon on 2 lawns
We can set an equation of proportionality for this or go straight ahead and equate to find the number of gallons required for 14 lawns.
1 gallon = 2 lawn
x gallon = 14 lawn
x = (14 * 1) / 2
x = 7 gallon
She will need 7 gallons to work on 14 lawns.
Learn more on proportions here;
https://brainly.com/question/2328454
#SPJ1
How many small squares in this rectangle should be shaded to represent
5 of
I
Answers
Answer:
Where's the picture
Step-by-step explanation:
The picture...
find the mean of brothers and sisters
Answers
The mean of brothers and sisters = 3
From the attached data set of brothers and sisters we can write the data values (frequency) as:
1, 5, 4, 2
We need to find the mean of brothers and sisters,
We know that the formula for the mean of data.
mean(\(\bar{x}\)) = sum of all data values / total number of data values
First we find the sum of all data values.
1 + 5 + 4 + 2 = 12
and the total number of data values = 4
Using above formula of mean,
mean(\(\bar{x}\)) = sum of all data values / total number of data values
mean(\(\bar{x}\)) = 12 / 4
mean(\(\bar{x}\)) = 3
Therefore, the required mean is: 3
Learn more about the mean here:
https://brainly.com/question/30891252
#SPJ1
Find the complete question below.

write a system of two quadratic equations that has solutions of (-3,-3) and (3,-3)
Answers
One system of quadratic equations that has solutions of (-3, -3) and (3, -3) is:
x^2 + y^2 = 18
x + y = 0
You can check that for x = -3 and y = -3, the left-hand side of both equations is equal to the right-hand side, and the same is true for x = 3 and y = -3.
Can someone help me please

Answers
Need help with the question below.
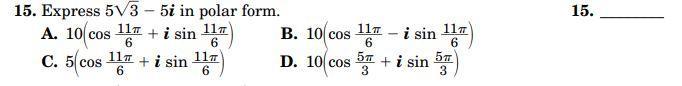
Answers
Answer:
A
Step-by-step explanation:
r=10 and the angle bln 5√3 and -5 is 330 or 11π/6
Can someone help me please?
ASAP

Answers
Answer:
y = 12 x = 12\(\sqrt{3}\)
Step-by-step explanation:
This is a 60, 90, 30. It's a special triangle.
2z = 24
z = 12
If x = z\(\sqrt{3}\)
then x = 12\(\sqrt{3}\)
y = z itself
So y = 12

Question 1 of 10
Suppose a normal distribution has a mean of 266 and a standard deviation of
12. What is P(x> 242)?
O A. 0.16
B. 0.475
C. 0.84
D. 0.975

Answers
0.975 is P(x ≥242) with a mean of 266 and standard deviation of 12

The required value of P(x> 242) = is 0.975 for normal distribution. Option D is correct.
The normal distribution has a mean of 266 and a standard deviation of
12. What is P(x> 242) is to determine.
Whata is normal distribution?Normal distributions can be altered to standard normal distributions by the formula:
Z = (X - μ)/σ
Where x is a value from the initial normal distribution, μ is the mean of the initial normal distribution, and σ is the standard deviation of the initial normal distribution. The standard normal distribution is periodically called the z distribution.
Now,
z = X - 266 /12
p(x > 242) = P [(X - 266)/12 ≥ (242 - 266)/12]
p(x > 242) = P [z ≥ -24/12]
p(x > 242) = P [z ≥ -2]
p(x > 242) = P [z ≤ 2]
p(x > 242) = 0.975 (from Z table).
Thus, the required value of P(x> 242) = is 0.975. Option D is correct.
Learn more about normal distribution here:
https://brainly.com/question/12421652
#SPJ2
I need help with this differential equation.

Answers
(i) The partial fraction decomposition of\(100/(x^7 * (10 - x))\) is\(100/(x^7 * (10 - x)) = 10/x^7 + (1/10^5)/(10 - x).\) (ii) The expression for t in terms of x is t = 10 ± √(100 + 200/x).
(i) To express the rational function 100/(\(x^7\) * (10 - x)) in partial fractions, we need to decompose it into simpler fractions. The general form of partial fractions for a rational function with distinct linear factors in the denominator is:
A/(factor 1) + B/(factor 2) + C/(factor 3) + ...
In this case, we have two factors: \(x^7\) and (10 - x). Therefore, we can express the given rational function as:
100/(\(x^7\) * (10 - x)) = A/\(x^7\) + B/(10 - x)
To determine the values of A and B, we need to find a common denominator for the right-hand side and combine the fractions:
100/(x^7 * (10 - x)) = (A * (10 - x) + B * \(x^7\))/(\(x^7\) * (10 - x))
Now, we can equate the numerators:
100 = (A * (10 - x) + B * \(x^7\))
To solve for A and B, we can substitute appropriate values of x. Let's choose x = 0 and x = 10:
For x = 0:
100 = (A * (10 - 0) + B * \(0^7\))
100 = 10A
A = 10
For x = 10:
100 = (A * (10 - 10) + B *\(10^7\))
100 = B * 10^7
B = 100 / 10^7
B = 1/10^5
Therefore, the partial fraction decomposition of 100/(\(x^7\) * (10 - x)) is:
100/(\(x^7\) * (10 - x)) = 10/\(x^7\) + (1/10^5)/(10 - x)
(ii) Given the differential equation: dx/dt = (1/100) *\(x^2\) * (10 - x)
We are also given x = 1 when t = 0.
To solve this equation and obtain an expression for t in terms of x, we can separate the variables and integrate both sides:
∫(1/\(x^2\)) dx = ∫((1/100) * (10 - x)) dt
Integrating both sides:
-1/x = (1/100) * (10t - (1/2)\(t^2\)) + C
Where C is the constant of integration.
Now, we can substitute the initial condition x = 1 and t = 0 into the equation to find the value of C:
-1/1 = (1/100) * (10*0 - (1/2)*\(0^2\)) + C
-1 = 0 + C
C = -1
Plugging in the value of C, we have:
-1/x = (1/100) * (10t - (1/2)\(t^2\)) - 1
To solve for t in terms of x, we can rearrange the equation:
1/x = -(1/100) * (10t - (1/2)\(t^2\)) + 1
Multiplying both sides by -1, we get:
-1/x = (1/100) * (10t - (1/2)\(t^2\)) - 1
Simplifying further:
1/x = -(1/100) * (10t - (1/2)\(t^2\)) + 1
Now, we can isolate t on one side of the equation:
(1/100) * (10t - (1/2)t^2) = 1 - 1/x
10t - (1/2)t^2 = 100 - 100/x
Simplifying the equation:
(1/2)\(t^2\) - 10t + (100 - 100/x) = 0
At this point, we have a quadratic equation in terms of t. To solve for t, we can use the quadratic formula:
t = (-(-10) ± √((-10)^2 - 4*(1/2)(100 - 100/x))) / (2(1/2))
Simplifying further:
t = (10 ± √(100 + 200/x)) / 1
t = 10 ± √(100 + 200/x)
Therefore, the expression for t in terms of x is t = 10 ± √(100 + 200/x).
For more such questions fraction,click on
https://brainly.com/question/78672
#SPJ8
fine the nth term of 11,13,15,17
Answers
The nth term of 11,13,15,17 is,
⇒ T (n) = 9 + 2n
Given that;
The sequence is,
11, 13, 15, 17, ....
Here, Common difference is,
13 - 11 = 2
15 - 13 = 2
Hence, Sequence is in Arithmetic sequence.
So, the nth term of 11,13,15,17 is,
⇒ T (n) = a + (n - 1)d
⇒ T (n) = 11 + (n - 1) 2
⇒ T (n) = 11 + 2n - 2
⇒ T (n) = 9 + 2n
Thus, The nth term of 11,13,15,17 is,
⇒ T (n) = 9 + 2n
Learn more about the Arithmetic sequence visit:
https://brainly.com/question/6561461
#SPJ1
What is an equation of the line that passes through the points (4, -2) and (8, – 7)?
Answers
Answer:
y = -1.25x + 3
Step-by-step explanation:
To see if the coordinate pairs are on this line, plug x into the equation above.
y = -5 + 3
y = -2, so (4, -2) is on that line.
y = -1.25(8) + 3
y = -10 + 3
y = -7, so (8, -7) is also on that line.
Answer:
y = -1.25x + 3
Step-by-step explanation:
i got it right
Which correctly shows the substitution step for the system?
y = x - 4
-4x - 6y = -16
O x-4 = -4x-6y
-4(x-4) - 6y = -16
O-4x-6(x-4) = -16
6y = x - 4
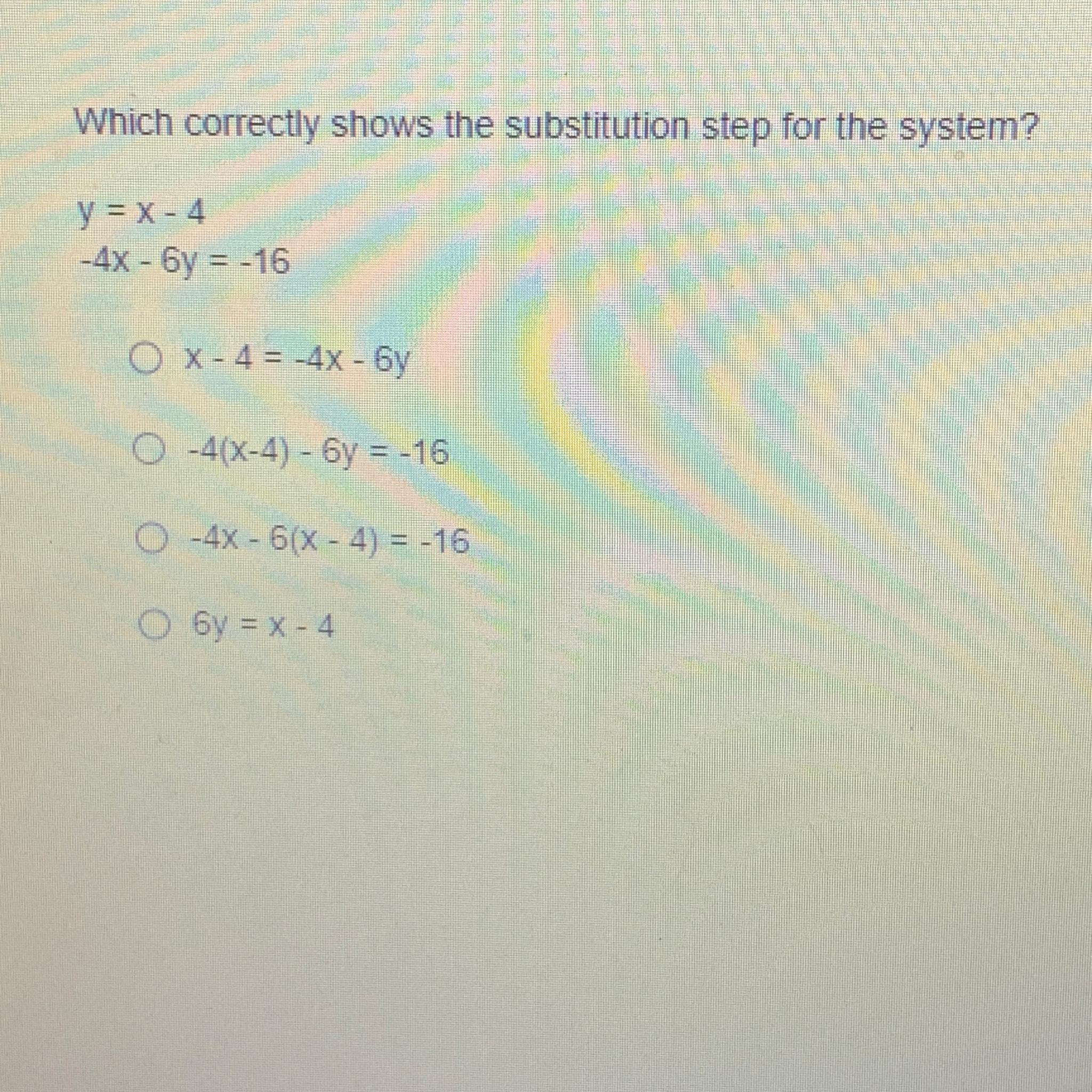
Answers
The solution to the system of equations is x = 4 and y = 0. In summary, the correct substitution step for the system is: -4x - 6(x - 4) = -16 .C answer is correct
To solve the given system of equations:
1) y = x - 4
2) -4x - 6y = -16
We can use the substitution method to eliminate one variable and solve for the other.
Step 1: Solve the first equation (1) for y in terms of x.
y = x - 4
Step 2: Substitute the expression for y from equation (1) into equation (2).
-4x - 6(x - 4) = -16
Step 3: Simplify and solve for x.
-4x - 6x + 24 = -16
-10x + 24 = -16
-10x = -16 - 24
-10x = -40
x = -40 / -10
x = 4
Step 4: Substitute the value of x back into equation (1) to solve for y.
y = 4 - 4
y = 0
Therefore, the solution to the system of equations is x = 4 and y = 0.
In summary, the correct substitution step for the system is:
-4x - 6(x - 4) = -16
By substituting the expression for y from equation (1) into equation (2) and simplifying, we obtain the equation -4x - 6y = -16, which can be further solved to find the values of x and y. C answer is correct
for more such question on substitution visit
https://brainly.com/question/22340165
#SPJ8
What’s one of the goals set out by the Healthy People 2010 program?:
a)
Ensuring that complaints against unfair billing are addressed
b)
Ensuring that private hospitals accept payment from any health insurance company
c)
Encouraging all employers to provide health insurance to their employees
d)
Eliminating the difference between the healthcare available to low and high income persons
Answers
Answer:
d i did the thing
Step-by-step explanation:
the following are the populations for the top twelve largest cities in the u. s. New York city, NY: 8,336,817 Los Angeles ca: 979.576 Chicago, il:2,693,976 Houston, Tx: 2,320,268 phoenix Az: 1,680,992 Philadelphia pa: 1,584,064 San Antonio Tx: 1, 547,253 San Diego ca: 1,423,851 Dallas Tx: 1,343,573 San Jose ca: 1,021,795 Austyn tx:978,908 Jacksonville Fl: 911,507. what is the mean population?, what is the median population?, what is the mode?, what is range?, what is the standard deviation?I need the standard deviation, I already did mode, mean, range, take the value of the population of each city, subtract the mode raised to 2, it does not give me the result
Answers
The mean is 2,071,798.33
The Median is 1,485,552
The range is 7,425,310
The standard deviation is given as 1961105.68
The mean population can be computed as:Mean = (Sum of all populations) / (Number of cities)
= (8,336,817 + 979,576 + 2,693,976 + 2,320,268 + 1,680,992 + 1,584,064 + 1,547,253 + 1,423,851 + 1,343,573 + 1,021,795 + 978,908 + 911,507) / 12
= 24,861,580 / 12
= 2,071,798.33
To find the median, we need to arrange the populations in increasing order and find the middle value. If we arrange these values, we get:
911,507, 978,908, 979,576, 1,021,795, 1,343,573, 1,423,851, 1,547,253, 1,584,064, 1,680,992, 2,320,268, 2,693,976, 8,336,817
Since there are 12 cities (an even number), the median would be the average of the 6th and 7th values:
Median = (1,423,851 + 1,547,253) / 2
= 1,485,552
The mode isn't applicable here as no city population repeats.
The range is the highest population minus the lowest population:
Range = 8,336,817 - 911,507
= 7,425,310
Standard deviation = (911507- 2068548.3333333)² + (978908 - 2068548.3333333)² + (979576 - 2068548.3333333)² + ( 1021795 - 2068548.3333333)² + (1343573- 2068548.3333333)² +( 1423851- 2068548.3333333)² + (1547253- 2068548.3333333)² +( 1584064- 2068548.3333333)² + (1680992- 2068548.3333333)² + ( 2320268- 2068548.3333333)² +(2693976- 2068548.3333333)² +( 8336817 - 2068548.3333333)² / 12
= 46151226311869 / 12
= 3845935525989.1
\(standard deviation = \sqrt{ 3845935525989.1}\)
= 1961105.6896529
Read more on mean , mode and median here https://brainly.com/question/14532771
#SPJ1
Hi am here spidey taylor

Answers
Answer:
this is my another account on brainly
If the expression 4x+3 is equal to 1 to the same value of x, what is the expression 4x+8 equal to for the same value of x?
Answers
Answer:
6
Step-by-step explanation:
4x + 3 = 1
4x =-2
x = -1/2 so 4x +8 =4(-1/2) +8=6
The units of an item available for sale during the year were as follows: Jan. 1 Inventory 50 units at $124 Mar. 10 Purchase 60 units at $132 Aug. 30 Purchase 20 units at $138 Dec. 12 Purchase 70 units at $142 There are 80 units of the item in the physical inventory at December 31. The periodic inventory system is used. Determine the ending inventory cost and the cost of goods sold by three methods. Round interim calculations to one decimal and final answers to the nearest whole dollar. blank Cost of Ending Inventory and Cost of Goods Sold Inventory Method Ending Inventory Cost of Goods Sold First-in, first-out (FIFO) $fill in the blank 1 $fill in the blank 2 Last-in, first-out (LIFO) fill in the blank 3 fill in the blank 4 Weighted average cost fill in the blank 5 fill in the blank 6
Answers
Ending Inventory Cost and Cost of Goods Sold using different inventory methods:
FIFO Method:
Ending Inventory Cost: $11,920
Cost of Goods Sold: $15,068
LIFO Method:
Ending Inventory Cost: $11,996
Cost of Goods Sold: $15,123
Weighted Average Cost Method:
Ending Inventory Cost: $11,974
Cost of Goods Sold: $15,087
Using the FIFO (First-In, First-Out) method, the cost of the ending inventory is determined by assuming that the oldest units (those acquired first) are sold last. In this case, the cost of the ending inventory is calculated by taking the cost of the most recent purchases (70 units at $142 per unit) plus the cost of the remaining 10 units from the March 10 purchase.
This totals to $11,920. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory at $124 per unit, 60 units from the March 10 purchase at $132 per unit, and 20 units from the August 30 purchase at $138 per unit), which totals to $15,068.
Using the LIFO (Last-In, First-Out) method, the cost of the ending inventory is determined by assuming that the most recent units (those acquired last) are sold first. In this case, the cost of the ending inventory is calculated by taking the cost of the remaining 10 units from the December 12 purchase, which amounts to $1,420, plus the cost of the 70 units from the August 30 purchase, which amounts to $10,576.
This totals to $11,996. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory, 60 units from the March 10 purchase, and 20 units from the August 30 purchase), which totals to $15,123.
Using the Weighted Average Cost method, the cost of the ending inventory is determined by calculating the weighted average cost per unit based on all the purchases. In this case, the total cost of all the purchases is $46,360, and the total number of units is 200.
Therefore, the weighted average cost per unit is $231.80. Multiplying this by the 80 units in the physical inventory at December 31 gives a total cost of $11,974 for the ending inventory. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory, 60 units from the March 10 purchase, and 20 units from the August 30 purchase), which totals to $15,087.
for such more questions on Cost
https://brainly.com/question/2292799
#SPJ8
True
The following table is a function.
X
y
1
5
-3 2
7 2 6 3
7
-4 5
9
8 4 1
7
1 0
True
False
Answers
Given statement: Here's the table with the values organized:
X | Y
-----
1 | 5
-3 | 2
7 | 2
6 | 3
7 | -4
5 | 9
8 | 4
1 | 7
1 | 0
This statement is False.
Because, The table provided is not a function because it does not have a clear and unique output value for each input value.
Since the X values 1 and 7 have multiple Y values, the given table is not a function.
In a function, each input value (X) must have a unique output value (y). However, in the given table, there are some input values, such as X = 7 and X = 1, that have multiple output values. For example, when X = 7, the table provides two output values, 2 and -4. Similarly, when X = 1, the table provides two output values, 5 and 0.
A function is a mathematical relationship between the input and output values, where each input value produces only one unique output value. Functions are used to represent many real-world scenarios, including calculating distances, temperatures, and profits. Therefore, it is crucial to ensure that the provided table represents a function by ensuring that each input value has a unique output value.
In conclusion, the table provided is not a function as it violates the one-to-one mapping between input and output values.
A function must have a clear and unique output value for each input value.
To determine if the given table represents a function, we need to make sure that each input (X value) corresponds to only one output (Y value).
Now let's check for any repeating X values with different Y values:
1 corresponds to both 5 and 7
7 corresponds to both 2 and -4.
False.
For similar question on value.
https://brainly.com/question/27882730
#SPJ11
The data set below has 7 values.
Find the mean absolute deviation for the data set.
If necessary, round your answer to the nearest hundredth.
15, 5, 12, 14, 18, 16, 4
Send data to calculator
Mean absolute deviation:
X
Answers
Answer:
4.29 (nearest hundredth)
Step-by-step explanation:
Given data set:
15, 5, 12, 14, 18, 16, 4To find the mean absolute deviation:
Step 1
Calculate the mean:
\(\textsf{Mean}=\dfrac{15+5+12+14+18+16+4}{7}=12\)
Step 2
Calculate the absolute deviations - how far away each data point is from the mean using positive distances.
\(\begin{array}{c|c}\vphantom{\dfrac12} \sf Data \; point & \sf Distance \; from \; mean\\\cline{1-2} \vphantom{\dfrac12} 15 & |15-12|=3\\\vphantom{\dfrac12} 5 & |5-12|=7\\\vphantom{\dfrac12} 12 & |12-12|=0\\\vphantom{\dfrac12} 14 & |14-12|=2\\\vphantom{\dfrac12} 18 & |18-12|=6\\\vphantom{\dfrac12} 16 & |16-12|=4\\\vphantom{\dfrac12} 4 & |4-12|=8\end{array}\)
Step 3
Add the absolute deviations together:
\(\implies 3+7+0+2+6+4+8=30\)
Step 4
Divide the sum of the absolute deviations by the number of data points:
\(\implies \dfrac{30}{7}=4.29\)
210÷14 Standard form help pleaee

Answers
Rewrite the equation in simplified slope-intercept form: 77-y=5x
Answers
The equation of the line in slope - intercept form is -
y = - 5x + 77.
What is the equation of a straight line in slope - intercept form?The equation of a straight line in slope - intercept form is -
y = mx + c
{m} - slope.
{c} - intercept along the y - axis.
Given is the equation as -
77 - y = 5x
We have the equation in the slope - intercept form as -
77 - y = 5x
y = 77 - 5x
y = - 5x + 77
Therefore, the equation of the line in slope - intercept form is -
y = - 5x + 77.
To solve more questions on straight lines, visit the link below -
brainly.com/question/28951560
#SPJ1
1. Write an expression for 8 less than 2
times a number.
Answers
Answer:
8<2x
Step-by-step explanation:
Answer:
8<2x
Step-by-step explanation:
I hope this helped! :D
