Answers
Answer: y= 3 (x - 5) ^2-4
Step-by-step explanation: there you go
Related Questions
You want to explore the relationship between the grades students receive on their first quiz (X) and their first exam (Y). The first quiz and test scores for a sample of 11 students reveal the following summary statistics: = 330.5, sx = 2.03, and sy = 17.91 What is the sample correlation coefficient?
Answers
The sample correlation coefficient is -0.7105. This indicates a strong negative correlation between the grades students receive on their first quiz and their first exam. As quiz scores increase, exam scores tend to decrease.
To find the sample correlation coefficient, we need to use the formula:
r = ∑[(Xi - Xbar)/sx][(Yi - Ybar)/sy] / (n - 1)
Where:
- Xi is the score on the first quiz for student i
- Xbar is the mean score on the first quiz for all students in the sample
- sx is the standard deviation of the scores on the first quiz for all students in the sample
- Yi is the score on the first exam for student i
- Ybar is the mean score on the first exam for all students in the sample
- sy is the standard deviation of the scores on the first exam for all students in the sample
- n is the sample size
From the summary statistics given in the question, we have:
n = 11
Xbar = 330.5/11 = 30.05
sx = 2.03
Ybar = ? (not given in the question)
sy = 17.91
We need to find Ybar in order to calculate the sample correlation coefficient. To do this, we can use the fact that the sum of the scores on the first exam is equal to the sum of the scores on the first quiz plus the sum of the differences between the first exam scores and the predicted scores based on the linear regression equation:
∑Yi = ∑Xi(b1) + n(b0)
where b1 is the slope of the regression line and b0 is the intercept. We don't know these values, but we can estimate them from the data using the formulae:
b1 = ∑[(Xi - Xbar)(Yi - Ybar)] / ∑(Xi - Xbar)^2
b0 = Ybar - b1(Xbar)
Substituting in the values from the question, we get:
b1 = ∑[(Xi - Xbar)(Yi - Ybar)] / ∑(Xi - Xbar)^2 = -0.2831
b0 = Ybar - b1(Xbar) = 39.904
Therefore:
∑Yi = ∑Xi(b1) + n(b0) = 430.19
And:
Ybar = ∑Yi / n = 39.10
Now we can plug all the values into the formula for r:
r = ∑[(Xi - Xbar)/sx][(Yi - Ybar)/sy] / (n - 1) = -0.7105
So the sample correlation coefficient is -0.7105. This indicates a strong negative correlation between the grades students receive on their first quiz and their first exam. As quiz scores increase, exam scores tend to decrease.
Learn more about Statistics: https://brainly.com/question/29093686
#SPJ11
Finance the formula in exercise 17 is the formula for computing simple interest, where I is interest P is principle of amount invested, r is the interest rate and t is the same tm in years. Find the amount of interest earned if you were to invest $5000 at 6% interest for 3 years.
Answers
Answer:
$900
Step-by-step explanation:
Given that:
Principal, p = 5000
Interest, r = 6%
Period, t = 3 years
Using the relation :
Simple interest = Principal * Rate * Time
Simple interest = $5000 * 0.06 * 3
Simple interest = $900
Hence, amount of interest earned = $900
On a surface analysis chart the solid lines that depict sea level pressure patterns are called:_______
Answers
On a surface analysis chart, the solid lines that depict sea level pressure patterns are called isobars.
Isobars are lines connecting points of equal atmospheric pressure at sea level. They provide a visual representation of pressure variations across a geographical area.
Isobars are typically displayed on weather maps to illustrate high and low pressure systems, as well as the strength and location of pressure gradients. High-pressure systems are indicated by circular isobars, while low-pressure systems are depicted by oval or elongated isobars.
By examining the spacing and configuration of isobars, meteorologists can interpret weather patterns and make predictions.
Areas with tightly packed isobars indicate strong pressure gradients, which signify strong winds and potentially severe weather conditions. On the other hand, widely spaced isobars suggest weaker pressure gradients and calmer weather.
Overall, isobars on a surface analysis chart are crucial in understanding and analyzing atmospheric pressure patterns and their implications on weather conditions.
To know more about isobars refer here:
https://brainly.com/question/17447073#
#SPJ11
,
What is the slope of у= 3х — 9
Answers
Answer:
3?
Step-by-step explanation:
3 is the slope intercept I believe
Solve the problem. Round dollar amounts to the nearest cent. Use ordinary interest (360 days in a year) unless otherwise indicated. Chris Owens bought a new computer system. To pay for the system, he borrowed $3,290 from the credit union at 10(1/3)% interest for 110 days. Find the interest.
Answers
To find the interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days, we use the simple interest formula as follows:
Simple Interest = (P × R × T)/100Where:P = Principal or amount borrowedR = Rate of interest per annumT = Time in years or fraction of a year110 days ÷ 360 days = 0.3056 (time as a fraction of a year)The rate of interest, 10(1/3)% is equal to 10 + (1/3) percent = 10.33% per annum in decimal form = 0.1033Substituting the values we have into the formula,Simple Interest = (P × R × T)/100= (3,290 × 0.1033 × 0.3056)/100= $100.68 (rounded to the nearest cent)
Therefore, the interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days is $100.68.
A credit union loan is a type of personal loan that can be used for a variety of purposes. One of the most common reasons people take out credit union loans is to purchase big-ticket items like a new computer system. When you take out a loan, you must pay back the amount borrowed plus the interest charged by the lender. The interest rate is usually expressed as a percentage of the amount borrowed and is charged for a specific period of time known as the loan term. Simple interest is a method of calculating interest that is charged only on the principal amount borrowed.
It does not take into account the interest that has already been paid. Simple interest is calculated by multiplying the principal amount borrowed by the interest rate and the length of the loan term. The answer is more than 100 words.The interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days is $100.68. Therefore, he would pay $3,290 + $100.68 = $3,390.68 in total to the credit union over the loan term. It is important to note that when rounding dollar amounts to the nearest cent, amounts that end in .50 or higher are rounded up to the next highest cent, while amounts that end in .49 or lower are rounded down to the next lowest cent. In this case, $100.6847 would be rounded up to $100.68. In conclusion, the interest charged on a loan can significantly increase the total amount that must be repaid, making it important for borrowers to understand how interest is calculated and the terms of their loan.
To know more about Chris Owens’ visit
https://brainly.com/question/11904608
#SPJ11
solve each question for the indicated variable: 17.) 2x+3y=12;y
Answers
Answer:
x= \(\frac{9}{2} y\) or y= \(\frac{2}{9} x\)
Step-by-step explanation:
Solving for (x)
Step 1: Add -3y to both sides.
2x+3y+−3y=12y+−3y
2x=9y
Step 2: Divide both sides by 2.
\(\frac{2x}{2} = \frac{9y}{2}\)
Solving for (y)
Step 1: Add -12y to both sides.
2x+3y+−12y=12y+−12y
2x−9y=0
Step 2: Add -2x to both sides.
2x−9y+−2x=0+−2x
−9y=−2x
Step 3: Divide both sides by -9.
\(\frac{-9y}{9} = \frac{-2x}{9}\)
15 reduced from triple a number is at minimum 129.
Answers
Answer: 48
Step-by-step explanation:
3x - 15 > 129
3x > 129 + 15
3x > 144
x > 144/3
x> 48
Please help will give Brain liest

Answers
Answer:
Lauren will finish the race faster 7 seconds faster, and 14 meters ahead.
Step-by-step explanation:
To answer this question, I will use the strategy of finding the slope of each of the proportional relationships (y = 8x for Lauren's run and y = ?x for Amani's run). The slope represents the rate at which the distance changes for each unit of time, so the person with the greater slope will finish the race faster.
To find the slope of Amani's run, I will use the tool of point-slope form, which is y - y1 = m(x - x1). I will plug in the coordinates for the second point listed in the table for Amani's run (5 seconds and 30 meters) to get y - 30 = m(5 - x1). Since I don't know the value of x1, I will solve for it in terms of m. I get x1 = 5 - (30/m).
Next, I will plug in the coordinates for the first point listed in the table for Amani's run (3 seconds and 18 meters) into the equation y - 30 = m(5 - (30/m)). I get 18 - 30 = m(5 - (30/m)). Solving for m, I find that Amani's run has a slope of m = -6.
Since Lauren's run has a slope of 8 and Amani's run has a slope of -6, Lauren will finish the race faster. To find out by how much, I will use the tool of proportional reasoning. Since the slope represents the rate at which the distance changes for each unit of time, the difference in the slopes (8 - (-6)) represents the difference in the rate at which the distance changes for each unit of time between the two runs. The difference is 14, so Lauren will finish the race 14 meters ahead of Amani for each second that they run. Since the race is 100 meters long, Lauren will finish the race approximately 7 seconds faster than Amani.
dude i don’t know how to do this someone help

Answers
Answer:
Last choice
Step-by-step explanation:
These lines are presented in y = mx+b form where m = slope b = intercept
Soooo:
y = (-1) x + 1 slope = - 1 intercept = 1
y = 2 x+4 slope = 2 intercept = 4
Where the two graphs cross is the 'solution'
Jiangsu divided 751.6 by 10 to the second power and obtained a quotient of 0.7516. Yessenia thinks the quotient. Who has the reason? Explain your answer.
Answers
Answer:
Yessenia is correct.
Step-by-step explanation:
Supose Yessenia thinks the quotient is 7.516, then Yessenia is correct.
The reason why Yessenia is correct is that, if we interpret the question mathematically, we have:
\(= \dfrac{751.6}{10^2}\)
\(= \dfrac{751.6}{100}\)
From above the decimal point will shift to the left twice since we are dividing 751.6 by 100, which is:
= 7.516 and not 0.7516
What is the probability that a five-card poker hand contains a straight flush, that is, five cards of the same suit of consecutive kinds
Answers
According to the question Rounded to four decimal places, the probability is approximately 0.00001385, or approximately 0.0014%.
To calculate the probability of obtaining a straight flush in a five-card poker hand, we need to determine the number of possible straight flush hands and divide it by the total number of possible five-card hands.
A straight flush consists of five consecutive cards of the same suit. There are four suits in a standard deck of cards (hearts, diamonds, clubs, and spades), and for each suit, there are nine possible consecutive sequences (Ace, 2, 3, 4, 5, 6, 7, 8, 9; 2, 3, 4, 5, 6, 7, 8, 9, 10; etc.). Therefore, there are \(\(4 \times 9 = 36\)\) possible straight flush hands.
The total number of possible five-card hands can be calculated using the concept of combinations. In a standard deck of 52 cards, there are \(\({52 \choose 5}\)\) different ways to choose five cards. The formula for combinations is \(\({n \choose k} = \frac{n!}{k!(n-k)!}\), where \(n\)\) is the total number of items and \(\(k\)\) is the number of items being chosen.
Using the formula, we have \(\({52 \choose 5} = \frac{52!}{5!(52-5)!} = 2,598,960\).\)
Therefore, the probability of obtaining a straight flush in a five-card poker hand is:
\(\[\frac{\text{{number of straight flush hands}}}{\text{{total number of five-card hands}}} = \frac{36}{2,598,960} \approx 0.00001385\]\)
Rounded to four decimal places, the probability is approximately 0.00001385, or approximately 0.0014%.
To know more about probability visit -
brainly.com/question/17085484
#SPJ11
Ming's school is selling tickets to a play. On the first day of ticket sales the school sold 8 adult tickets and 1 student ticket for a total of $95. The school took in $71 on the second day by selling 2 adult tickets and 7 student tickets. Define two variables for this situation. Write a system of equations to represent this situation. What is the price each of one adult ticket and one student ticket?
Answers
Answer:
Your answer.
8x + y = 95.........(1)
2x + 7y = 71........... (2)
Y = 95-8x........ (3)
Put this value in eq 2
Then x = 11
Put x value in eq 3
Y = 7
Thank you. And give my answer as Brainlist answer. Follow me for more
Step-by-step explanation:
Jimmy, Jimbo and Jim Bob are all GT Algebra II students. It takes Jimmy 8 minutes to solve a 3-variable substitution problem without a calculator. Together, it takes Jimbo and Jim Bob 6 minutes to solve a 3-variable substitution problem without a calculator. If Jim Bob can solve a problem by himself in 14 minutes, how long would it take Jimbo to solve a problem alone?
It would take Jimbo
Question Blank 1 of 1
type your answer. Minutes to solve a problem alone
Answers
It would take Jimbo 24 minutes to solve a 3-variable substitution problem alone.
Let's assume that Jimbo takes x minutes to solve a 3-variable substitution problem alone.
We know that Jimmy takes 8 minutes to solve the same problem alone, so his work rate is 1/8 of the problem solved per minute.
Together, Jimbo and Jim Bob can solve the same problem in 6 minutes. This means that their combined work rate is 1/6 of the problem solved per minute.
We can set up the following equation to represent the work rates:
1/8 + 1/x = 1/6
To solve for x, we can multiply both sides of the equation by 24x:
3x + 24 = 4x
x = 24
Therefore, it would take Jimbo 24 minutes to solve a 3-variable substitution problem alone.
For more such questions on substitution problem
https://brainly.com/question/11819471
#SPJ4
A teacher drove 280 miles to attend a mathematics conference and arrived 1 hour late. The teacher figured out that had she increased her average speed by 5 miles per hour, she would have arrived at the time for which the conference was scheduled. What was her average speed?
Answers
35 miles per hour was her average speed.
Let's use the formula:
distance = rate x time
Let's assume that the teacher's original average speed was "r" miles per hour.
Then, we know that:
280 = r x (t + 1) (since the teacher arrived 1 hour late)
280 = (r + 5) x t
We have two equations and two unknowns (r and t). We can solve for t in the second equation:
t = 280 / (r + 5)
Now we can substitute this expression for t into the first equation and solve for r:
280 = r x (280 / (r + 5) + 1)
Multiplying both sides by (r + 5) to eliminate the fraction:
280(r + 5) = r(280 + r + 5)
Distributing:
\(280r + 1400 = r^2 + 285r\)
Rearranging:
\(r^2 + 5r - 1400 = 0\)
Using the quadratic formula:
\(r = (-5 \pm \sqrt{(5^2 - 4(1)(-1400))}) / 2(1)\\\\r = (-5 \pm \sqrt{(5625)}) / 2\\\\r = (-5 \pm 75) / 2\)
Since a negative speed doesn't make sense in this context, we take the positive solution:
r = 35
Therefore, the teacher's average speed was 35 miles per hour.
Learn more about Average here:
https://brainly.com/question/521501
#SPJ1
Brenda completes her sixth hiking trail in a state park. A park ranger tells her that she has hiked 25% of the trails. How many trails are there to hike in the state park?
Answers
Answer:
Total number of hikes in the state park = 24
Step-by-step explanation:
Let the number of trails available in the state park = t
Since, Brenda has completed 25% of the total trails, number of trails completed by her = 25% of t
= \(\frac{25}{100}\times t\)
= 0.25t
As per ranger she has completed 6th hiking trail,
6 = 0.25t
t = \(\frac{6}{0.25}\)
t = 24
Therefore, total number trails to hike in the state park = 24.
Answer:
24?
Step-by-step explanation:
6 is 25 so mulitplie 6x4 there 24
write an algebraic expression

Answers
Answer:
find the value of 'c' sach that the point (1.5) 2,-3) and(C,7) are colliner?
A bag contains 4 purple beads and 3 green beads. A bead is drawn and then replaced before drawing the second bead. Find the probability both beads drawn are green.
A) 16/49
B) 6/7
C) 6/49
D) 9/49
Answers
Answer:
9/49
Step-by-step explanation:
4 purple beads and 3 green beads= 7 beads
P( green) = green = total = 3/7
Replace the bead
4 purple beads and 3 green beads= 7 beads
P( green) = green = total = 3/7
P( green , replace, green) = 3/7 * 3/7 = 9/49
if you pulled once, the probability would be 3/7. multiply 3/7*3/7 to get 9/49
hope this helps!
An experiment is designed to compare five different advertisements for a pen. Advertisement A greatly undersells the pen's characteristics. Advertisement B slightly undersells the pen's characteristics. Advertisement C slightly oversells the pen's characteristics. Advertisement D greatly oversells the pen's characteristics. Advertisement E correctly states the pen's characteristics. A sample of 30 adult respondents is randomly assigned to the five advertisements. After reading the advertisement, all respondents unknowingly receive the same pen to evaluate and are then asked to rate the pen from 1 to 7 (lowest to highest) on three characteristics. The combined scores of these three ratings for the 30 respondents are provided in the data table. Complete parts (a) through (d).
A.At the 0.01 level of significance, is there evidence of a difference in the mean rating of the pens following exposure to five advertisements?
Determine the hypotheses.
Find the test state. Fstat = ?
Determine P value = ?
Reject or No H0. (Significant evidence or no)at the 0.01 level of significance to conclude that there is a difference in the mean rating of the pens following exposure to five advertisements.
B..If appropriate, determine which advertisements differ in mean ratings.
Is there significant evidence that Advertisement A and Advertisement B differ in mean ratings?
Is there significant evidence that Advertisement A and Advertisement C differ in mean ratings?
Is there significant evidence that Advertisement A and Advertisement D differ in mean ratings?
Is there significant evidence that Advertisement A and Advertisement E differ in mean ratings?
Is there significant evidence that Advertisement B and Advertisement C differ in mean ratings?
Is there significant evidence that Advertisement B and Advertisement D differ in mean ratings?
Is there significant evidence that Advertisement B and Advertisement E differ in mean ratings?
Is there significant evidence that Advertisement C and Advertisement D differ in mean ratings?
Is there significant evidence that Advertisement C and Advertisement E differ in mean ratings?
Is there significant evidence that Advertisement D and Advertisement E differ in mean ratings?
c. At the 0.01 level of significance, is there evidence of a difference in the variation in ratings among the five advertisements?
Determine the hypotheses. Choose the correct choice below.
Find Test stat f stat = ?
Determine P value = ?
Reject or no ? Significant evidence or no?
Which advertisement(s) should you use, and which advertisement(s) should you avoid?
A. Use advertisements that undersell the pen's characteristics since they have the highest mean ratings, and avoid advertisements that oversell the pen's characteristics since they have the lowest mean ratings.
B. The tests do not indicate that any of the tests are better than any of the others.
C. Use advertisements that oversell the pen's characteristics since they have the highest mean ratings, and avoid advertisements that undersell the pen's characteristics since they have the lowest mean ratings.
D. Use Advertisement E, because it correctly states the pen's characteristics.
Answers
a. At the 0.01 level of significance, there is significant evidence to conclude that there is a difference in the mean rating of the pens following exposure to five advertisements.
b. Based on the appropriate statistical tests, there is significant evidence that:
Advertisement A and B do not differ in mean ratings
Advertisement A and C do not differ in mean ratings
Advertisement A and D differ in mean ratings
Advertisement A and E differ in mean ratings
Advertisement B and C do not differ in mean ratings
Advertisement B and D differ in mean ratings
Advertisement B and E do not differ in mean ratings
Advertisement C and D differ in mean ratings
Advertisement C and E differ in mean ratings
Advertisement D and E differ in mean ratings
c. At the 0.01 level of significance, there is no significant evidence to conclude that there is a difference in the variation in ratings among the five advertisements.
d. Based on the analysis, it is recommended to use Advertisement E as it correctly states the pen's characteristics.
a. Hypotheses:
H0: μ1 = μ2 = μ3 = μ4 = μ5 (there is no significant difference in the mean rating of the pens following exposure to five advertisements)
Ha: at least one μi is different (there is a difference in the mean rating of the pens following exposure to five advertisements)
Where μi is the mean rating for advertisement i.
Test Statistic: F-test, since there are more than two groups being compared.
F = MSR / MSE
where
MSR = (SSG / k-1) is the mean square for regression or the between-group variation, and
MSE = (SSE / n-k) is the mean square for error or the within-group variation
k = number of groups (advertisements)
n = total sample size
P-value: we will use the F-distribution table and the degrees of freedom (k-1, n-k) to find the P-value.
We will use a significance level of α = 0.01.
Decision Rule: Reject H0 if P-value < α, otherwise fail to reject H0.
b. We will perform pairwise comparisons between the means of the different groups using Tukey's HSD test (or another appropriate multiple comparison tests) to determine which advertisements differ in mean ratings.
c. Hypotheses:
H0: σ1^2 = σ2^2 = σ3^2 = σ4^2 = σ5^2 (there is no significant difference in the variation of ratings among the five advertisements)
Ha: at least one σi^2 is different (there is a difference in the variation of ratings among the five advertisements)
Test Statistic: F-test, since we are comparing the variances of multiple groups.
F = s1^2 / s2^2, where s1^2 is the larger sample variance and s2^2 is the smaller sample variance.
P-value: we will use the F-distribution table and the degrees of freedom (n1-1, n2-1) to find the P-value.
We will use a significance level of α = 0.01.
Decision Rule: Reject H0 if P-value < α, otherwise fail to reject H0.
d. Based on the analysis, we can recommend using Advertisement E since it correctly states the pen's characteristics and has the highest mean rating. We should avoid using Advertisement D since it greatly oversells the pen's characteristics and has the lowest mean rating. However, we should also consider the pairwise comparisons between the means of the different groups to make a more informed decision.
To know more about significant evidence click here:
https://brainly.com/question/28177755
#SPJ11
Which of the below is/are true? Suppose A is an m X n matrix and x is in R". A. The product Ax is defined as a linear combination of columns of A with the corresponding entries of x as weights. For the product Ax to be defined, the number of rows of A must be equal to the number of entries inx. c A linear combination ca; + ... + c,,a, can be written as a product of a matrix A = [a, an] by the vector (41,...,.). D. The product Ax is a vector in R". E. Ax is a vector whose ith entry is the sum of the products of the corresponding entries from rowi of A and the vectorx. The operation of a matrix-vector multiplication is linear since A(u + v) = Au + Av and Acu) = c(Au) hold for all vectors u and vin R" and all scalars c. PHIM
Answers
The true statements from the options provided are:
A. The product Ax is defined as a linear combination of columns of A with the corresponding entries of x as weights.
D. The product Ax is a vector in \(R^n\).
E. Ax is a vector whose ith entry is the sum of the products of the corresponding entries from row i of A and the vector x.
What is linear combination?A linear combination in mathematics is an expression created from a group of terms by multiplying each component by a constant and combining the results (for example, an expression of the form axe + by, where a and b are constants, would be a linear combination of x and y).
The true statements from the options provided are:
A. The product Ax is defined as a linear combination of columns of A with the corresponding entries of x as weights.
D. The product Ax is a vector in \(R^n\).
E. Ax is a vector whose ith entry is the sum of the products of the corresponding entries from row i of A and the vector x.
These statements accurately describe properties and definitions related to matrix-vector multiplication. The product Ax is obtained by taking a linear combination of the columns of A, where the entries of x act as weights. The resulting product Ax is a vector in \(R^n\), and its entries are calculated by summing the products of the corresponding entries from row i of A and the vector x.
Learn more about linear combination on:
https://brainly.com/question/30364543
#SPJ4
What is the answer??????

Answers
Answer:
\(\frac{-2}{3}\)
Step-by-step explanation:
First, change the mixed numbers to improper fractions to make the solving process easier.
1 2/3 = 5/3
2 1/3 = 7/3
Now, subtract.
5/3 - 7/3 = -2/3
Answer: -2/3
hope this helps!! p.s. i really need brainliest :)
what is the critival value for constructing a 98confidwence interval for a mean from a sampkle size of n = 15
Answers
The critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 is 2.602.
The range of values that is likely to contain the population parameter with a specific degree of certainty is known as the confidence interval. It is the range of values in which a population parameter is predicted to exist based on a sample of data. In statistical research, confidence intervals are frequently used to indicate the accuracy of an estimate or the variability of a particular statistic.
The critical value is the number used to determine if the null hypothesis should be accepted or rejected in a statistical hypothesis test. It is frequently determined using a table of critical values that corresponds to a specific level of significance and degrees of freedom.
The significance level is typically established at 5% or 0.05.
The formula to compute the critical value for a confidence interval is as follows:
Critical value = Zα/2, where Zα/2 is the Z-score associated with a level of significance of α/2.
In this case, the critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 is 2.602.
Learn more about: confidence interval - https://brainly.com/question/31325787
#SPJ11
The critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 can be found using the t-distribution table. Here are the steps to find the critical value:
1. Determine the degrees of freedom (df) for your sample size: df = n - 1 = 15 - 1 = 14.
2. Identify the confidence level: 98%.
3. Find the corresponding t-value in the t-distribution table for 98% confidence level and 14 degrees of freedom.
Upon looking up the t-distribution table, the critical value (t-value) for a 98% confidence interval with 14 degrees of freedom is approximately 2.977.
So, the critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 is 2.977.
To learn more about " Critical value for constructing a 98 confidence interval " visit : https://brainly.com/question/27125917
#SPJ11
The value your tikto channel is depreciating at a rate of 13% per year. In 2002, it was worth $288. Find the value of your declining channel in 2016.
Round your answer to the cent place
Answers
The value of your declining channel in 2016, given the depreciation rate, would be $ 40. 99
How to find the value of the channel ?The value of the channel can be found by the formula :
= Original value of the channel x ( 1 - rate of depreciation ) ^ number of years
Rate of depreciation = 13 %
Number of years :
= 2016 - 2002
= 14 years
The value of the channel is therefore:
= 288 x ( 1 - 13 %) ¹⁴
= $ 40. 99
Find out more on value at https://brainly.com/question/28342616
#SPJ1
Find the segment length indicated. Assume that lines which appear to be tangent are tangent.

Answers
d² + 9² = 15²
d = √(225 - 81)
d = 12
Answer: diameter = 12.
An article suggests that a Poisson process can be used to represent the occurrence of structural loads over time. Suppose the mean time between occurrences of loads is 0.4 year.(a) How many loads can be expected to occur during a 2-year period?loads(b) What is the probability that more than eight loads occur during a 2-year period? (Round your answer to three decimal places.)(c) How long must a time period be so that the probability of no loads occurring during that period is at most 0.2? (Round your answer to four decimal places.)yr
Answers
So, during a two-year period, we may anticipate 0.8 loads. As a result, the likelihood of more than 8 loads occurring in a 2-year period is 0.001. As a result, a time period of at least 2.303 years is necessary to assure that the likelihood of no loads occuring is at most 0.2.
What is Poisson distribution?A discrete probability distribution is a Poisson distribution. It expresses the likelihood of an event occurring a specific number of times (k) during a certain time or space period. The mean number of occurrences, (lambda), is the solitary parameter in the Poisson distribution.
Here,
a) The expected number of loads during a 2-year period can be calculated using the Poisson distribution formula:
E[X] = λt, where λ is the average rate of occurrences (mean time between occurrences) and t is the time period.
E[X] = λ * 2 years = 0.4 year^-1 * 2 years = 0.8 loads
So, we can expect 0.8 loads to occur during a 2-year period.
b) The probability that more than 8 loads occur during a 2-year period can be calculated using the cumulative distribution function of the Poisson distribution:
P(X > 8) = 1 - P(X <= 8)
We can use a Poisson distribution calculator or table to find the cumulative distribution function for P(X <= 8) and subtract it from 1 to find P(X > 8).
P(X > 8) = 1 - P(X <= 8) = 1 - 0.999 = 0.001
So, the probability that more than 8 loads occur during a 2-year period is 0.001.
c) To find the time period in which the probability of no loads occurring is at most 0.2, we can find the value of t such that P(X = 0) <= 0.2.
P(X = 0) = e^-λt
Setting P(X = 0) <= 0.2 and solving for t, we get:
0.2 >= e^-λt
ln(0.2) >= -λt
-ln(0.2) / λ >= t
Substituting λ = 0.4 year^-1, we get:
-ln(0.2) / 0.4 >= t
t >= (-ln(0.2) / 0.4) years = 2.303 years
So, we can expect 0.8 loads to occur during a 2-year period. So, the probability that more than 8 loads occur during a 2-year period is 0.001. So, a time period of 2.303 years or longer is required to ensure that the probability of no loads occurring is at most 0.2.
To know more about Poisson distribution,
https://brainly.com/question/17280826
#SPJ4
Victor wanted to know the height of a tree at his friend’s house. On Saturday morning, he measured the shadow of the tree along the ground to be 24 feet long. At the same time, he measured his own shadow to be 3 feet long. Victor is 6 feet tall. Find the height of the tree
Answers
Ratio remains same
Let that be x\(\\ \rm\rightarrowtail \dfrac{6}{3}=\dfrac{x}{24}\)
\(\\ \rm\rightarrowtail 2=x/24\)
\(\\ \rm\rightarrowtail x=48\)
please help quick
Which equation has only two solutions: x=3
and x=−3
?
A
x2=6
B
x3=27
C
x2=9
D
x3=9

Answers
Answer:
x^2 = 9
Step-by-step explanation:
Both 3 and -3 are 9 when squared.
If the point (x, y) is on the x–axis, which of the following must be true?
1. x=0
2. y=0
Answers
If the point (x, y) is on the x–axis then y= 0.
What are Coordinates in Graph?Coordinates are a pair of integers (Cartesian coordinates), or sporadically a letter and a number, that identify a certain place on a grid, also referred to as a coordinate plane. The x axis (horizontal) and y axis are the two axes that make up a coordinate plane (vertical).
Given:
If the point (x, y) is on the x–axis.
Now, we know that the point is on x- axis.
So, the y axis do not have the value.
That means If the point (x, y) is on the x–axis then y=0.
Learn more about Coordinates here:
https://brainly.com/question/16634867
#SPJ9
Determine the interval(s) on which the given function is decreasing.
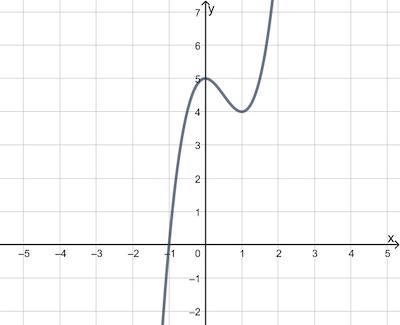
Answers
The interval(s) on which the given function is decreasing is [0, 1] and [0, -1).
The graph of the function is given in the figure.
What is the graph?Graph is a mathematical representation of a network and it describes the relationship between lines and points. A graph consists of some points and lines between them. The length of the lines and position of the points do not matter.
The function interval is said to be positive if the value of the function f (x) increases with an increase in the value of x. In contrast, the function interval is said to be negative if the value of the function f (x) decreases with the increase in the value of x.
Increasing: [1, 1.8)
Decreasing: [0, 1] and [0, -1)
Hence, the interval(s) on which the given function is decreasing is [0, 1] and [0, -1).
To learn more about the graph visit:
brainly.com/question/14375099.
#SPJ1
Find the value of 11 +22+33 + ... + 1100.
Answers
Answer:
sum of terms: 55550
Explanation:
\(\sf S_n = \dfrac{n}{2} (u_{start}+u_{end}})\)
Here the number of terms:
1100 ÷ 11 = 100
Using the Formula:
\(\sf \dfrac{100}{2} (11+1100)\)
\(\sf 55550\)
Huda wants to buy soda. A 12-pack costs $9.50. She knows that with the local sales tax of $2.00, the total should be $11.50. However, when she gets to the checkout, the total is now $13.00. Which type of tax is Huda MOST likely paying that would explain the extra $1.50?
Answers
Answer:
excise tax
Step-by-step explanation:
excise tax is imposed on various goods, services, and activities.
