()()PLZZ HELP MY PARENTS SAID I CANT CELEBRATE THANKSGIVING IF THI ISNT DONE PLZZZ HELP IM GIVING 25 DOLLAR AMAZON CARD TO WHOEVER HELP AND DOES ALL OF THESE + 100 POINTS +BRAINLIEST





Answers
Related Questions
In the algebraic expression 5x + 8y – 12z, the values 5, 8, and –12 are _____
Answers
Answer:
Coefficients!!!
Step-by-step explanation:
They're numbers that are multiplied by a variable.
Answer:
Step-by-step explanation:
I believe the answer would be coefficients. Coefficients are the number that is being multiplied by the variable.
Which of the following is an example of distributive property of multiplication over addition for rational numbers?
A
−14 × {23 + (−47)} = [−14 × 23] + [−14 × (−47)]
B
−14 × {23 + (−47)} = [14 × 23] − (−47)
C
−14 × {23 + (−47)} = 23 + (−14) × −47
D
−14 × {23 + (−47)} = {23 + (−47)} − 14
Answers
Your answer: A −14 × {23 + (−47)} = [−14 × 23] + [−14 × (−47)] This example demonstrates the distributive property of multiplication over addition for rational numbers, which states that for any rational numbers a, b, and c: a × (b + c) = (a × b) + (a × c).
The correct answer is A: −14 × {23 + (−47)} = [−14 × 23] + [−14 × (−47)]. This is an example of the distributive property of multiplication over addition for rational numbers because we are multiplying −14 by the sum of 23 and −47, and we can distribute the multiplication to each term inside the parentheses by multiplying −14 by 23 and −14 by −47 separately, and then add the two results together. This is the basic definition of the distributive property of multiplication over addition. Option B shows the distributive property of multiplication over subtraction, option C shows the product of multiplication and addition, and option D is not a valid equation.
Learn more about rational here:
https://brainly.com/question/20850120
#SPJ11
if i fail a class for one semester will i fail6th grade
Answers
Answer:
yes you will because you need to pass all subject now if your in home school if you fail one subject you would have to see because not all schools are the same so... yeah but in my opinion if you fail one subject you do fail 6 grade I mean thats what I think I am in 9th grade so I dont remember that much
Step-by-step explanation:
4 Tuan wants to add trim only around the edges of the
gate in problem 3. About how much trim does he need?
A
20.28 feet
C
34.56 feet
B 32.56 feet
D
39.12 feet
help please i have 5 missing math assignments
Answers
Answer:
✔ ∅ B 32.56 feetStep-by-step explanation:
4 Tuan wants to add trim only around the edges of the
gate in problem 3. About how much trim does he need?
✘ O A 20.28 feet
✘ O C 34.56 feet
✔ ∅ B 32.56 feet
✘ O D 39.12 feet
I don’t understand what I’m suppose to do. Can someone please help?

Answers
From the 64 values in the table on the left, count how many fall within the given ranges under the "classes" column in the table on the right. The "frequency" is the number of values in the data that belong to a given "class".
For example, "< -16.0" means "values below -16.0". Only one number satisfies this: -16.2 (first row, third column). So the frequency for this class is just 1.
Then for the range "-15.9 - 13.0", which probably means "numbers between 15.9 and -13.0, inclusive", the frequency is 0 because every number in the table is larger than the ones in this range.
And so on.
Which ordered pair can be plotted together with these four points, so that the resulting graph still represents a function?

Answers
The ordered pair that can be plotted together with these four points, so that the resulting graph still represents a function is (2, -1).
option C.
Which ordered pair can be plotted together?The ordered pair that can be plotted together with these four points, so that the resulting graph still represents a function is determined as follows;
The four points include;
A = (1, 2)
B = (2, - 3)
C = (-2, - 2)
D = (-3, 1)
The ordered pair that can be plotted together with these four points, must fall withing these coordinates. Going by this condition we can see that the only option that meet this criteria is;
(2, - 1)
Thus, the ordered pair that can be plotted together with these four points, so that the resulting graph still represents a function is (2, -1).
Learn more about ordered pairs here: https://brainly.com/question/30467126
#SPJ1
An artificial soccer pitch is 91 meters long and 43 meters wide. If the cost of the pitch is AED 20 per square meter. What is the cost of installing the pitch????
Answers
The Cost of installing the artificial soccer pitch is $5360
A rectangle is a quadrilateral (has four sides and four angles) in which opposite sides are parallel and equal.
The soccer pitch us rectangle in shape. Hence:
Perimeter of soccer pitch = 2(length + width) = 2(91 + 43) = 268 meters
Cost of installing the pitch = $20 per meter * 268 meters = $5360
The Cost of installing the artificial soccer pitch is $5360
Find out more on perimeter at: https://brainly.com/question/16596982
Williams lunch at Buffalo wild wings cost $13 without tax he leaves the waitress a tip of 17% of the cost of the launch without tax what is the total cost of lunch including tip without tax?
Answers
Answer:
$15.21
Step-by-step explanation:
The total cost of the lunch without tax is $13. If you want to find the cost of the tip, you have to find 17% of 13. To find this you do 13×0.17 which is 2.21 dollars. Now add this to the original price of your lunch, $13, to get $15.21.
Find the value(s) of c guaranteed by the Mean Value Theorem for Integrals for the function over the given interval. (Round your answer to four decimal places. Enter your answers as a comma-separated list.) f(x)
Answers
The value of c by the Mean Value Theorem for Integrals for the function over the given integral is 6.25.
In the question, we are asked to find the value(s) of c guaranteed by the Mean Value Theorem for Integrals for the function f(x)=5√x,[4,9] over the given interval.
The given function is f(x)=5√x,[4,9].
First we calculate the function value at the endpoints of the interval.
f(4) = 5√4 = 5*2 = 10.
f(9) = 5√9 = 5*3 = 15.
We substitute x = c in the given function, to get:
f(c) = 5√c.
Now, we calculate f'(c) using the formula:
f'(c) = (f(b) - f(a))/(b - a),
or, f'(c) = (f(9) - f(4))/(9 - 4),
or, f'(c) = (15 - 10)(9 - 4),
or, f'(c) = 5/5 = 1.
Differentiating the original function, gives us f'(x) = 5/(2√x).
Substituting x = c in this gives us f'(c) = 5/(2√c).
Equating this to f'(c) = 1 gives us:
5/(2√c) = 1,
or, √c = 5/2,
or, c = 25/4,
or, c = 6.25.
Thus, the value of c by the Mean Value Theorem for Integrals for the function over the given integral is 6.25.
Learn more about the Mean value theorem at
https://brainly.com/question/17111829
#SPJ4
The provided question is incomplete. The complete question is:
"Find the value(s) of c guaranteed by the Mean Value Theorem for Integrals for the function over the given interval. (Round your answer to four decimal places. Enter your answers as a comma-separated list.)
f(x)=5√x,[4,9]."
Study the number line shown. Match the question with the correct letter on the number line.
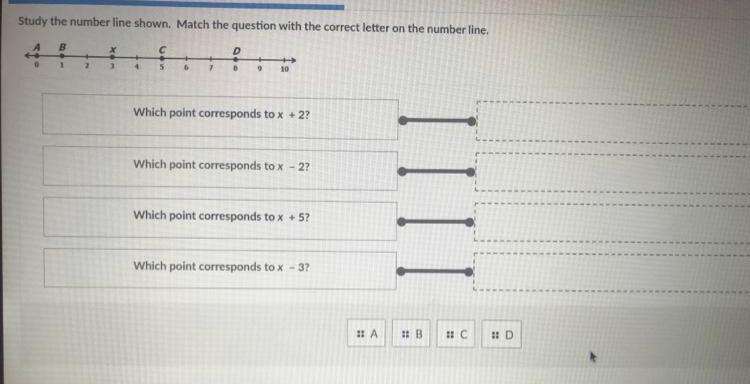
Answers
Answer:
C,B,D,A
Step-by-step explanation:
Start at 3(X) and move based on the question
Determine the boundedness and monotonicity of the sequence with a_n = (0.35)^n|. a) decreasing: bounded below by 0 and above by 0.35. b) increasing: bounded below by 0 and above by 0.35. c) decreasing: bounded below by 1 and above by 0.35. d) nonincreasing, bounded below by 0 and above by 0.35. e) nondecreasing: bounded below by 1 and above by 0.35
Answers
The boundedness and monotonicity of the sequence with a_n = (0.35)^n|. a) decreasing: bounded below by 0 and above by 0.35.
The given sequence is a_n = (0.35)^n. To determine its boundedness and monotonicity, let's analyze the terms and their progression.
Boundedness:
Since 0 < 0.35 < 1, raising 0.35 to increase powers will result in terms that are smaller than the previous term but always greater than 0. Thus, the sequence is bounded below by 0. The first term of the sequence is (0.35)^1 = 0.35, and all subsequent terms are smaller. Therefore, the sequence is also bounded above by 0.35.
Monotonicity:
As we established, each term in the sequence is smaller than the previous one, as we are multiplying by a factor between 0 and 1. This means that the sequence is decreasing.
Putting these two findings together, the correct answer is:
a) decreasing: bounded below by 0 and above by 0.35.
Visit here to learn more about sequence:
brainly.com/question/21961097
#SPJ11
-9-52 to the power of 2
Answers
when multiplying two powers that have the same base, you can add the exponents. In this example, you can see how it works. Adding the exponents is just a short cut! The "power rule" tells us that to raise a power to a power, just multiply the exponents.
What is the percent
increase from 70 to 77?
Answers
Percentage change = 10%
We can use the formula:
Percent change = \(\frac{New-Old}{Old}\) x 100
Percent change = \(\frac{77-70}{70}\)x100
Percent change = \(\frac{7}{70}\) x 100
Percent change = 0.1 x 100
Percent change = 10%
Answer: 53.9
Step-by-step explanation:
Suppose that, from measurements in a microscope, you determine that a certain bacterium covers an area of 1. 50μm2. Convert this to square meters.
Answers
Converting 1. 50μm² to square meters gives 1. 5 × 10 ^-11
What is conversion of units?Conversion of units is defined as the conversion of different units of measurement for the same quantity, mostly through multiplicative conversion factors.
From the information given, we are to convert micrometers to square meters
Note that:
1 micrometer ( μm²) = 10^-12m²
Given 1. 50μm² = xm²
cross multiply
x = 1. 50 × 10^-12
x = 1. 50 × 10^-12
x = 1. 50 × 10^-12
x = 1. 5 × 10 ^-11 square meters
Thus, converting 1. 50μm² to square meters gives 1. 5 × 10 ^-11
Learn more about conversion here:
https://brainly.com/question/16851332
#SPJ1
difer from the true proportion by more than 2% ? A previous study indicates that the proportion of lefthanded sclontists is 9%. Round up to the nearest whicie number. Duestion 13 A. 1.218 B. 1,109 C. 14 D.767
Answers
The total number of samples will be 1109 .
Given ,
Margin of error 0.02
Here,
According to the formula,
\(Z_{\alpha /2} \sqrt{pq/n}\)
Here,
p = proportions of scientist that are left handed
p = 0.09
n = number of sample to be taken
Substitute the values,
\(Z_{0.01} \sqrt{0.09 * 0.91/n} = 0.02\\ 2.33 \sqrt{0.09 * 0.91/n} = 0.02\\\\\\\)
n ≈1109
Thus the number of samples to be taken will be approximately 1109 .
Know more about proportions,
https://brainly.com/question/31548894
#SPJ4
solve the system by graphing y= -2x y-1/2x-5
Answers
The solution to the system of equations, y = -2x and y = 1/2x - 5, is solved graphically to be (2, -4) as shown in the image attached below.
How to Solve a System of Equations by Graphing?To solve a system of equations by graphing, plot both lines of the equations on a coordinate plane to determine the coordinates of the point where both lines intersect each other.
The solution is the point where they intersect.
Given the system of equations:
y = -2x
y = 1/2x - 5
The graph in the attachment shows the line of y = -2x (red line), and that of y = 1/2x - 5 (blue line).
Both lines intersect at point (2, -4). Therefore, the solution to the system of equations is: (2, -4).
Learn more about solution of a system on:
https://brainly.com/question/13729904
#SPJ1

An international organization must decide how to spend the $2,000,000 they have been allotted for famine relief in a remote area. They expect to divide the money between buying rice at $38.5/sack and beans at $35/sack. The number, P, of people who would be fed if they buy x sacks of rice and y sacks of beans is given by P= 1.1x + y - 108 What is the maximum number of people that can be fed, and how should the organization allocate its money?
Answers
To maximize the number of people that can be fed, subject to the constraint that the total cost of rice and beans cannot exceed $2,000,000. Let's first rewrite the cost constraint as an equation:
38.5x + 35y = 2,000,000
Now we can rewrite the expression for P in terms of one variable.
How optimal allocation for famine relief funds?
To find the maximum number of people that can be fed, which means we need to maximize the function P= 1.1x +y - 108 subject to the budget constraint:
38.5x + 35y = 2,000,000
First, we can rewrite the budget constraint as:
77x + 70y = 4,000,000y - 108.
To do this, we can use the constraints provided by the budget and the prices of rice and beans. Let's assume that the organization will spend all of the $2,000,000, so we have the equation:
38.5x + 35y = 2,000,000
This represents all the possible combinations of sacks of rice and beans that can be bought with the given budget.
To make the problem easier to work with, we can solve for y in terms of x:
y = (2,000,000 - 38.5x) / 35
Now we can substitute this expression for y into the function for P:
P = 1.1x + (2,000,000 - 38.5x) / 35 - 108
Simplifying this, we get:
P = (14x - 3250) / 35
To maximize P, we can take the derivative and set it equal to zero:
dP/dx = 14/35 = 0
Solving for x, we get:
x = 100,000/14
x = 7,142.857
Since we can't buy a fraction of a sack, we round down to the nearest whole number:
x = 7,142
Now we can use the equation we derived earlier to find the corresponding value of y:
y = (2,000,000 - 38.5 x) / 35
y = (2,000,000 - 38.5(7,142)) / 35
y = 22,000
Therefore, the maximum number of people that can be fed is:
P = 1.1 x + y - 108
P = 1.1(7,142) + 22,000 - 108
P = 30,346
So, the organization should buy 7,142 sacks of rice and 22,000 sacks of beans to feed the maximum number of people.
Learn more about constraint
brainly.com/question/13643976
#SPJ11
Do the details of Example 3 as follows:
(a) Verify that the four matrices in (7.14) are all orthogonal and verify the stated values of their determinants.
(b) Verify the products C = AB and D = BA in (7.15).
(c) Solve (7.16) to find the reflection line.
(d) Analyze the transformation D as we did C.
Answers
a) The four matrices given in (7.14) are:
\(�1=12(111−1),\)
det
\((�1)=−1�2=15(2−1−12),det(\)
\(�2)=1�3=110(122−1),det(�3)=−1�4=113(3−2−2−3),det\)
\((�4)=1Q 1 Q 2 Q 3 Q 4 = 2 1 ( 11 1−1 ),det(Q 1 )=−1= 5 1 ( 2−1 −12\)
),det(Q
\(2 )=1= 10 1 ( 12 2−1 ),det(Q 3 )=−1= 13 1 ( 3−2 −2−3 ),det(Q 4 )=1\)
To verify that these matrices are orthogonal, we need to check that $Q_iQ_i^T=Q_i^TQ_i=I$ for $i=1,2,3,4$. Let's check this for $Q_1$ as an example:
\(�1�1�=12(111−1)(111−1)=(1001)=�Q 1\)
Q
\(1T = 21 ( 11 1−1 )( 11 1−1 )=( 10 01 )=Iand�1��1=12(111−1)(111−1)=(1001)=�Q 1T Q 1 = 21 ( 11\)
\(1−1 )( 11 1−1 )=( 10 01 )=I\)
Thus, $Q_1$ is orthogonal. Similarly, we can check that $Q_2$, $Q_3$, and $Q_4$ are orthogonal as well.
(b) The product $C=AB$ can be computed as follows:
\(�=��=�4�3�2�1=113(3−2−2−3)110(122−1)15(2−1−12)12(111−1)=1130(1−32−32−1)C\)
\(=AB=Q 4 Q 3 Q 2 Q 1 = 13 1 ( 3−2 −2−3 ) 10 1 ( 12 2−1 ) 5 1 ( 2−1\)
\(−12 ) 2 1 ( 11 1−1 )= 130 1 ( 1−3 2 −3 2 −1 )\)
The product $D=BA$ can be computed as follows:
\begin{aligned}
D &= BA = Q_1Q_2Q_3Q_4 \\
&= \frac{1}{\sqrt{2}}\
Learn more about matrices here:
https://brainly.com/question/11367104
#SPJ11
find the steady state solution of the heat conduction equation
Answers
The steady-state solution of the heat conduction equation refers to the temperature distribution that remains constant over time. This occurs when the heat flow into a system is balanced by the heat flow out of the system.
To find the steady-state solution of the heat conduction equation, follow these steps:
1. Set up the heat conduction equation: The heat conduction equation describes how heat flows through a medium and is typically given by the formula:
q = -k * A * dT/dx,
where q represents the heat flow, k is the thermal conductivity of the material, A is the cross-sectional area through which heat flows, and dT/dx is the temperature gradient in the direction of heat flow.
2. Assume steady-state conditions: In the steady-state, the temperature does not change with time, which means dT/dt = 0.
3. Simplify the heat conduction equation: Since dT/dt = 0, the equation becomes:
q = -k * A * dT/dx = 0.
4. Apply boundary conditions: Boundary conditions specify the temperature at certain points or surfaces. These conditions are essential to solve the equation. For example, you might be given the temperature at two ends of a rod or the temperature at the surface of an object.
5. Solve for the steady-state temperature distribution: Depending on the specific problem, you may need to solve the heat conduction equation analytically or numerically. Analytical solutions involve techniques like separation of variables or Fourier series expansion. Numerical methods, such as finite difference or finite element methods, can be used to approximate the solution.
It's important to note that the exact method for solving the heat conduction equation depends on the specific problem and the boundary conditions given. However, the general approach is to set up the heat conduction equation, assume steady-state conditions, simplify the equation, apply the boundary conditions, and solve for the steady-state temperature distribution.
Know more about steady-state solution here:
https://brainly.com/question/15073499
#SPJ11
write the single-precision representation for the following decimal number. (-0.625) or -5/8 final results must be in hex
Answers
The single-precision representation for the decimal number -0.625 or -5/8 in hexadecimal is: BF40 0000.
To find the single-precision representation of the decimal number -0.625 or -5/8, we'll follow these steps:
1. Convert the decimal to binary.
2. Normalize the binary representation.
3. Determine the exponent and add the bias.
4. Convert the mantissa to the required 23-bit representation.
5. Combine the sign bit, exponent, and mantissa.
6. Convert the final binary representation to hexadecimal.
Step 1: Convert the decimal to binary.
\(-0.625 = -5/8 = -1/2 - 1/8\)
In binary, this is \(-0.101 (1/2 = 0.1, and 1/8 = 0.001)\)
Step 2: Normalize the binary representation.
Normalized: -1.01 x 2^(-1)
Step 3: Determine the exponent and add the bias.
Exponent = -1, and the bias for single-precision is 127.
Exponent + bias = -1 + 127 = 126
In binary, this is 01111110.
Step 4: Convert the mantissa to the required 23-bit representation.
Normalized mantissa: 1.01
The first digit (1) is omitted, and we only take the digits after the binary point: 01
23-bit representation: 01000000000000000000000
Step 5: Combine the sign bit, exponent, and mantissa.
Sign bit for a negative number is 1.
Final binary representation: 1 01111110 01000000000000000000000
Step 6: Convert the final binary representation to hexadecimal.
1 0111 1110 0100 0000 0000 0000 0000 0000 = BF40 0000
for such more questions on single-precision
https://brainly.com/question/29107209
#SPJ11
I will mark brainliest
A car begins at rest and accelerates. Its distance in meters, C(t), can be determined as a function
of time in seconds, t, by the formula C^1(t) = 4t^2.
A second car, 150 meters ahead, is traveling at
a constant speed of 20 meters per second. Its distance, (C^2), in meters can be determined as
a function of time, t, in seconds by the formula C^2(t) = 20t+ 150. How long after the first car
accelerates will the cars be side by side?
Round to the nearest hundredth, if necessary.
Answers
Here, we are required to determine how long after the first car accelerates will the cars be side by side.
The cars will be side by side at Time, t = 9.11seconds after the first car accelerates.
The position of each car is given by the function of its distance, i.e C1 and C2.
At the point when the cars are side by side;
C^1(t) must be equal to C^2(t).
Mathematically;
C^1(t) = C^2(t)C^1(t) = C^2(t)i.e 4t² = 20t + 150Therefore, we have;
2t - 10t -75 = 0By solving quadratically;
We have ; Time, t = 9.11 seconds. (to the nearest hundredth).
Read more:
https://brainly.com/question/18920363
Find the absolute maximum and absolute minimum values of the function f(x)=x^3−12x^2−27x+8 over each of the indicated intervals.
(a) Interval = [−2,0]. (b) Interval = [1,10]. (c) Interval = [−2,10].
Answers
The value of Absolute maximum are (a) 8, (b) -30.36, (c) -10 and the Absolute minimum are (a) -10, (b) -362.39, (c) -362.39.
We are given a function:f(x) = x³ - 12x² - 27x + 8We need to find the absolute maximum and absolute minimum values of the function f(x) over each of the indicated intervals. The intervals are:
a) Interval = [-2, 0]
b) Interval = [1, 10]
c) Interval = [-2, 10]
Let's begin:
(a) Interval = [-2, 0]
To find the absolute max/min, we need to find the critical points in the interval and then plug them in the function to see which one produces the highest or lowest value.
To find the critical points, we need to differentiate the function:f'(x) = 3x² - 24x - 27
Now, we need to solve the equation:f'(x) = 0Using the quadratic formula, we get: x = (-b ± √(b² - 4ac)) / 2a
Substituting the values of a, b, and c, we get:
x = (-(-24) ± √((-24)² - 4(3)(-27))) / 2(3)x = (24 ± √(888)) / 6x = (24 ± 6√37) / 6x = 4 ± √37
We need to check which critical point lies in the interval [-2, 0].
Checking for x = 4 + √37:f(-2) = -10f(0) = 8
Checking for x = 4 - √37:f(-2) = -10f(0) = 8
Therefore, the absolute max is 8 and the absolute min is -10.(b) Interval = [1, 10]
We will follow the same method as above to find the absolute max/min.
We differentiate the function:f'(x) = 3x² - 24x - 27
Now, we need to solve the equation:f'(x) = 0Using the quadratic formula, we get: x = (-b ± √(b² - 4ac)) / 2a
Substituting the values of a, b, and c, we get:
x = (-(-24) ± √((-24)² - 4(3)(-27))) / 2(3)
x = (24 ± √(888)) / 6
x = (24 ± 6√37) / 6
x = 4 ± √37
We need to check which critical point lies in the interval [1, 10].
Checking for x = 4 + √37:f(1) = -30.36f(10) = -362.39
Checking for x = 4 - √37:f(1) = -30.36f(10) = -362.39
Therefore, the absolute max is -30.36 and the absolute min is -362.39.
(c) Interval = [-2, 10]
We will follow the same method as above to find the absolute max/min. We differentiate the function:
f'(x) = 3x² - 24x - 27
Now, we need to solve the equation:
f'(x) = 0
Using the quadratic formula, we get: x = (-b ± √(b² - 4ac)) / 2a
Substituting the values of a, b, and c, we get:
x = (-(-24) ± √((-24)² - 4(3)(-27))) / 2(3)x = (24 ± √(888)) / 6x = (24 ± 6√37) / 6x = 4 ± √37
We need to check which critical point lies in the interval [-2, 10].
Checking for x = 4 + √37:f(-2) = -10f(10) = -362.39
Checking for x = 4 - √37:f(-2) = -10f(10) = -362.39
Therefore, the absolute max is -10 and the absolute min is -362.39.
Learn more about function at
https://brainly.com/question/31956232
#SPJ11
Suppose you are holding a stock and there are three possible outcomes. The good state happens with 20% probability and 18% return. The neutral state happens with 55% probability and 9% return. The bad state happens with 25% probability and -5% return. What is the expected return? What is the standard deviation of return? What is the variance of return?
Answers
The expected return is 0.072 (or 7.2%), the standard deviation is approximately 0.2006 (or 20.06%), and the variance is approximately 0.04024 (or 4.024%).
To calculate the expected return, standard deviation, and variance of the stock, we can use the following formulas:
Expected Return (E(R)):
E(R) = Σ(Probability of State i × Return in State i)
Standard Deviation (σ):
σ = √[Σ(Probability of State i × (Return in State i - Expected Return)^2)]
Variance (Var):
Var = σ^2
Let's calculate these values for the given probabilities and returns:
Expected Return (E(R)):
E(R) = (0.20 × 0.18) + (0.55 × 0.09) + (0.25 × -0.05)
= 0.036 + 0.0495 - 0.0125
= 0.072
Standard Deviation (σ):
σ = √[(0.20 × (0.18 - 0.072)^2) + (0.55 × (0.09 - 0.072)^2) + (0.25 × (-0.05 - 0.072)^2)]
= √[(0.20 × 0.108)^2 + (0.55 × 0.018)^2 + (0.25 × (-0.122)^2)]
= √[(0.0216) + (0.0005445) + (0.0181)]
≈ √0.0402445
≈ 0.2006
Variance (Var):
Var = σ^2
= (0.2006)^2
≈ 0.04024
Learn more about standard deviation here: brainly.com/question/475676
#SPJ11
Please help, I need the answer as soon as possible!!!!

Answers
The simplified power of \((\frac{\sqrt[4]{m} }{6\sqrt[4]{m^3} })^{-1}\)⁻¹ is 6√m and a = 1/2.
To simplified the power of the equation, we have to do some converstion to the equation.
Remember that:
\(x^{-1}=\frac{1}{x}\)
\(\sqrt[b]{x^a} =x^{\frac{a}{b} }\)
\(\frac{x^{a} }{x^{b} }\) = xᵃ⁻ᵇ
Notice that the power outside the brackets are negative, then we need to flip the equation to eliminate the negative sign:
\((\frac{\sqrt[4]{m} }{6\sqrt[4]{m^3} })^{-1}\) = \(\frac{6\sqrt[4]{m^3} }{\sqrt[4]{m} }\)
= \(\frac{6m^{3/4} }{m^{1/4} }\)
= \(6m^{(3/4 - 1/4)}\)
= \(6m^{2/4}\)
= \(6m^{1/2}\)
6mᵃ = \(6m^{1/2}\\\)
a = 1/2
Learn more about Simplified Power here: brainly.com/question/11955026
#SPJ1
One side of a square is (x+3) units. The
perimeter of the square is 32 units. What
is X?
Answers
Answer:
x = 5
Step-by-step explanation:
So the perimeter of a square is 4 times the side length.
4 (x+3) = 32 is the equation we can make out with the given information.
Solve for x:
Distribute the 4 to the terms inside the parenthesis; 4x + 12 = 32
Subtract 12 from both sides; 4x = 20
Divide both sides by 4; x = 5
By isolating x, we get 5 as the value of x.
PLEASE HELP ASAP NEED NOW !!! For the given word problem, identify the rate of change.
Gasoline at a particular gas station costs $2.78 per gallon. If Cory buys $18 of gas, how many gallons did he buy?
(1 point)
a. $2.78
b. g
c. $18
d. 1
Answers
Answer:
6½ gallons
Step-by-step explanation:
Givem the cost of 1gallon of gas = $2.78. . If Cory buys $18 of gas, we are to find the number of gallons did he buy. To do that we will use the equality method as shown;
$2.78 ,= 1gallon
$18 = x gallon
Cross multiply
2.78 × x = 1×18
2.78x = 18
Divide through by 2.78
2.78x/2.78 = 18/2.78
.x = 6.5
Hence Cory buys about 6½ gallons of gas for $18
35 X 6.7
What is this answer
Answers
Answer:
234.5
Step-by-step explanation:
Answer:
234.5
Step-by-step explanation:
Which of the following means a study used a bivariate correlational design?
a. presence of measured variables
b. use of correlational stats
c. inclusion of quantitative variables
d. depiction of bar graph
Answers
among the given options, the use of correlational statistics OPTION B is the most reliable indicator that a study employed a bivariate correlational design.
A bivariate correlational design is characterized by the examination of the relationship between two quantitative variables. In this context, the use of correlational statistics is a key indicator of this design. Correlational statistics, such as correlation coefficients (e.g., Pearson's r), are employed to assess the strength and direction of the relationship between the variables under investigation.
The presence of measured variables, inclusion of quantitative variables, or depiction of a bar graph are not definitive indicators of a bivariate correlational design. Measured variables can be present in various study designs, including experimental ones. Similarly, quantitative variables can be utilized in different types of studies, such as experimental, quasi-experimental, or observational designs. The depiction of a bar graph, which is commonly used to illustrate categorical data, does not inherently imply the use of a bivariate correlational design.
learn more about bivariate correlational here:
https://brainly.com/question/31797663
#SPJ11
In circle I, IJ=4 and mJIK∠=90∘ Find the area of shaded sector. Express your answer as a fraction times π.
Answers
The area of the shaded sector is 4π square units.
To find the area of the shaded sector, we need to calculate the central angle formed by the sector. In this case, we are given that the angle JIK is 90 degrees, which means it forms a quarter of a full circle.
Since a full circle has 360 degrees, the central angle of the shaded sector is 90 degrees.
Next, we need to determine the radius of the circle. The line segment IJ represents the radius of the circle, and it is given as 4 units.
The formula to calculate the area of a sector is A = (θ/360) * π * r², where θ is the central angle and r is the radius of the circle.
Plugging in the values, we have A = (90/360) * π * 4².
Simplifying, A = (1/4) * π * 16.
Further simplifying, A = (1/4) * π * 16.
Canceling out the common factors, A = π * 4.
Hence, the area of the shaded sector is 4π square units.
Therefore, the area of the shaded sector, expressed as a fraction times π, is 4π/1.
In summary, the area of the shaded sector is 4π square units, or 4π/1 when expressed as a fraction times π.
For more such questions on area, click on:
https://brainly.com/question/25292087
#SPJ8
Three roots of a fifth degree polynomial function f(x) are –2, 2, and 4 i. Which statement describes the number and nature of all roots for this function?.
Answers
The correct option is f(x) has three real roots and two imaginary roots.
Given
Three roots of a fifth-degree polynomial function f(x) are –2, 2, and 4 i.
Complex conjugateThe complex conjugate of a complex number is the number with an equally real part and an imaginary part equal in magnitude but opposite in sign.
It is given that the roots of the fifth-degree polynomial function are -2, 2, and 4+i.
Since the degree of f(x) is 5, therefore there are 5 roots of the function either real or imaginary.
According to the complex conjugate root theorem, if a+ib is a root of a polynomial function f(x), then a-ib is also a root of the polynomial f(x).
Since 4+i is a root of f(x), so by complex conjugate rot theorem 4-i is also a root of f(x).
From the given data the number of real roots is 2 and the number of 2. The number of complex roots is always an even number, so the last root must be a real number.
Therefore, the correct option is f(x) has three real roots and two imaginary roots.
To know more about imaginary roots click the link given below.
https://brainly.com/question/1375079
Answer:
f(x) has three real roots and two imaginary roots.
Step-by-step explanation:
on edge 2023