Answers
Answer:
a > 8
Step-by-step explanation:
a - 3 > 5
a > 8
Related Questions
TU = 1 - x, UB = 4x + 17, TB = -3x
Answers
A line is the shortest distance between two points. The value of x from the given parameters is 3
Line segmentationA line is defined as the shortest distance between two points. Given the following parameters
TU = 1 - x,
UB = 4x + 17,
TB = -3x
According to the addition postulate;
TU + UB = TB
Substitute the given parameters to have:
1 - x + 4x + 17 = -3x
Collect the like terms to have:
1+3x+17 = -3x
3x+3x = -1-17
Simplify
6x = -18
Divide both sides by 6
6x/6 = -18/6
x = -18/6
x = -3
Hence the value of x from the given parameters is 3
learn more on addition postulate here: https://brainly.com/question/2134445
#SPJ1
A plumber earns $43 for a repair job, plus an additional $56 per hour he works. On Tuesday, he
completed 3 repair jobs and earned a total of more than $700.
Part A: Write an inequality that can be used to determine h, the number of hours the plumber
worked on Tuesday.

Answers
Answer:
A. 150+75h>600
B. More than 6 hours
Step-by-step explanation:
A plumber earns $50 for a repair job, so he will earn $150 for three repair jobs.
Let h be the number of hours the plumber worked on Tuesday. He earns $75 per hour worked, so he will earn $75h in h hours.
In total, the plumber earned $(150 + 75h)
A. On Tuesday, he completed 3 repair jobs and earned a total of more than $600. Thus
150+75h>600
B. Solve this inequality. Subtract 150:
150+75h-150>600-150
75h>450
Divide by 75:
h> 450/75
h>6
This means, the plumber worked more than 6 hours.
Please help me and answer

Answers
4 > |x+1| + 2
======================================================
Explanation:
Choice A can be ruled out because the result of any absolute value is never negative.
This means |x+1| cannot be smaller than -3.
In other words: -3 > |x+1| has no solutions
Similarly, choice B also leads to "no solutions" because we subtract 2 from both sides to get -1 > |x+2|. Therefore, we rule out choice B as well.
------------------
Choice C can be solved through these steps
2 < |x+3| - 2
2+2 < |x+3|
4 < |x+3|
|x+3| > 4
x+3 > 4 or x+3 < -4
x > 4-3 or x < -4-3
x > 1 or x < -7
x < -1 or x > 1
The graph of this will have open holes at -7 and 1. Then you shade to the left of -7 and to the right of 1. This does not match the graph given to us.
We'll rule out choice C.
-------------------
Choice D can be solved through these steps
4 > |x+1| + 2
4-2 > |x+1|
2 > |x+1|
|x+1| < 2
-2 < x+1 < 2
-2-1 < x < 2-1
-3 < x < 1
The graph will have open holes at -3 and 1, with shading in between. This matches perfectly with the given graph.
This is why choice D is the answer.
What angular resolution would you need to see the Sun and Jupiter as distinct points of light? Express your answer in arcseconds to two significant figures. Jupiter 195| ΑΣΦ % ? 11 Suppose you were looking at our own solar system from a distance of 6.0 light-years.
Answers
An angular resolution of 0.56 arcseconds is required to see the Sun and Jupiter as separate objects. This is an extremely small angle and would necessitate the use of a large telescope.
Angular resolution is defined as the minimum angle between two objects that enables a viewer to see them as distinct objects rather than as a single one. A better angular resolution corresponds to a smaller minimum angle. The angular resolution formula is θ = 1.22 λ / D, where λ is the wavelength of light and D is the diameter of the telescope. Thus, the angular resolution formula can be expressed as the smallest angle between two objects that allows a viewer to distinguish between them. In arcseconds, the answer should be given to two significant figures.
To see the Sun and Jupiter as distinct points of light, we need to have a good angular resolution. The angular resolution is calculated as follows:
θ = 1.22 λ / D, where θ is the angular resolution, λ is the wavelength of the light, and D is the diameter of the telescope.
Using this formula, we can find the minimum angular resolution required to see the Sun and Jupiter as separate objects. The Sun and Jupiter are at an average distance of 5.2 astronomical units (AU) from each other. An AU is the distance from the Earth to the Sun, which is about 150 million kilometers. This means that the distance between Jupiter and the Sun is 780 million kilometers.
To determine the angular resolution, we need to know the wavelength of the light and the diameter of the telescope. Let's use visible light (λ = 550 nm) and assume that we are using a telescope with a diameter of 2.5 meters.
θ = 1.22 λ / D = 1.22 × 550 × 10^-9 / 2.5 = 2.7 × 10^-6 rad
To convert radians to arcseconds, multiply by 206,265.θ = 2.7 × 10^-6 × 206,265 = 0.56 arcseconds
The angular resolution required to see the Sun and Jupiter as distinct points of light is 0.56 arcseconds.
This is very small and would require a large telescope to achieve.
In conclusion, we require an angular resolution of 0.56 arcseconds to see the Sun and Jupiter as separate objects. This is an extremely small angle and would necessitate the use of a large telescope.
To know more about angular resolution visit:
brainly.com/question/31858807
#SPJ11
Mila and Nadia have R480 between them.
Mila has 7 times as much as Nadia.
How much does each of them have?
Answers
Answer:
Mila= 420 Nadia= 60
Step-by-step explanation:
Let's call Mila 7x. And x to Nadia. The two of them had a total of 480s.
Then we say 7x + x. Their total is 8x. So 480 = 8x. We divide both sides by 8. Here x = 60. Since Mila is 7x, we find Mila as 7.60 = 420, and since Nadia as x, we find Nadia as 1.60 = 60.
If there is any place you don't understand, you can ask.
#Achievements
which of the following are examples of numerical data? (select all that apply)

Answers
The examples of numerical data is daily UV index and maximum temperature.
It is required to choose the examples of numerical data.
What is the data ?A collection of facts, such as numbers, words, measurements, observations. Data is information that has been translated into a form that is efficient for movement or processing.
Given:
Numerical data represent values that can be measured and put into a logical order. Examples of numerical data are height, weight, age, number of movies watched, IQ, etc.
In the given option the examples of numerical data is daily UV index and maximum temperature.
Therefore, the examples of numerical data is daily UV index and maximum temperature.
Learn more details about data here:
https://brainly.com/question/10980404
#SPJ2
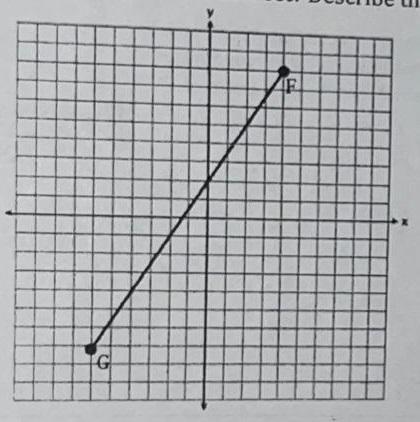
Loule and Nicky were asked to find point P that divides the directed line segment FG so that the ratio of FP to PG is 4 to 1. Loule says the coordinate of point P is (-4,-4), while Nicky says the coordinate of point P is (2, 5). Who is correct? Describe the mistake that was made by the student who was incorrect
Answers
Using ratio and proportion, Louie is correct.
Ratio is defined as the relationship between two quantities. On the other hand, proportion is defined as the equality between two or more ratios.
From the given graph (see attached photo), the coordinates of Point F and Point G is (4, 8) and (-6, -7).
If the ratio of FP to PG is 4 to 1, then the ratio of the horizontal distance and vertical distance between the two endpoints is also 4 to 1.
FP : PG = 4 : 1
FP/PG = 4/1 = 4
x-coordinate of P
(4 - x)/(x - -6) = 4
(4 - x) = 4(x + 6)
4 - x = 4x + 24
-5x = 20
x = -4
y-coordinate of P
(8 - y)/(y - -7) = 4
(8 - y) = 4(y + 7)
8 - y = 4y + 28
-5y = 20
y = -4
Hence, the coordinates of Point P is (-4, -4).
Therefore, Louie is correct, while Nicky is mistaken probably while setting up the proportion and solving for the coordinates.
Learn more about ratio and proportion here: https://brainly.com/question/23431895
#SPJ4
The number of millions of people in a certain country who lived below the poverty level for the year can be modeled by y=0.008x2 -0.4518+46,888 where x is the number of years after 1990.
a. The vertax of the graph of this function is a:
Answers
The vertex of the graph of function y = 0.008x² - 0.4518 + 46,888 is a point at (0, 46,888). The function models the number of millions of people in a certain country who lived below the poverty level.
The given function that models the number of millions of people in a certain country who lived below the poverty level for the year is:
y = 0.008x² - 0.4518 + 46,888
where x is the number of years after 1990. To find the vertex of the graph of this function, let us first convert the given function to the vertex form of a quadratic equation:
y = a(x - h)² + kWe
are given the function as:
y = 0.008x² - 0.4518 + 46,888
Comparing with the vertex form of a quadratic equation:
y = a(x - h)² + k
We get: a = 0.008,h = 0 and k = 46,888
Substituting these values in the vertex form of a quadratic equation, we get:
y = 0.008(x - 0)² + 46,888y = 0.008x² + 46,888
Now we can see that the vertex of the graph of the function
y = 0.008x² + 46,888 is at the point (0, 46,888).
Therefore, the answer is: The vertex of the graph of this function is a point at (0, 46,888).
Learn more about quadratic equation here: https://brainly.com/question/22364785
#SPJ11
Which inequality is graphed on the coordinate plane?

Answers
Answer:
E is the answer
Step-by-step explanation:
There are 10 students in a class: 6 boys and 4 girls.
If the teacher picks a group of 3 at random, what is the probability that everyone in the group is a boy?
Answers
Answer:
1/ 6
Step-by-step explanation:
Therefore, the required probability is 1/6.
Answer:
1/6
Step-by-step explanation:
Think of drawing 1 student at a time without replacement.
First drawing:
p(boy) = 6/10
Second drawing:
p(boy) = 5/9
Third drawing:
p(boy) = 4/8
p(3 boys) = 6/10 * 5/9 * 4/8 = 3/5 * 5/9 * 1/2 = 3/18 = 1/6
Answer: 1/6
45^2 can be found out by 4 x ____ x 100 + ____ = ____
Answers
Explanation:
45^2 = 2025
45^2 = 4 x 5 x 100 + 25 = 2025
3. In this problem, we will solve the following recurrence using the substitution method (i.e., induction). Assume T(1)=0,T(2)=1 and that the recurrences below define T(n) for n>2 : 3.1. Try T(n)=
n. Does the recurrence hold? Which side is bigger? Show your calculations. 3.2. Try T(n)=n. Does the recurrence hold? Which side is bigger? Show your calculations. 3.3. Try T(n)=n
2
. Does the recurrence hold? Which side is bigger? Show your calculations. 3.4. Prove your result formally using the substitution method. (Hint: try T(n) with a constant offse That is, T(n)=n
p
+c for some c∈R and p>0. Note that parts 1−3 correspond to c=0 and p=1/2, p=1,p=2, respectively. Now, solve for p and c.)
Answers
None of the functions T(n) = n, T(n) = n, and T(n) = \(n^2\) satisfy the recurrence relation T(n), but assuming T(n) = \(n^p\) + c, where p > 0 and c is a constant offset, we can derive the conditions for p and c that satisfy the recurrence relation.
To solve the recurrence relation T(n) using the substitution method, we'll try different functions T(n) and analyze whether the recurrence holds and which side is bigger.
1. Try T(n) = n:
T(1) = 1
T(2) = 2
T(n) = n
Now let's check if the recurrence holds:
T(n) = 2T(n-1) + T(n-2)
= 2(n-1) + (n-2)
= 2n - 2 + n - 2
= 3n - 4
We see that T(n) = 3n - 4, which is not equal to n. Therefore, T(n) = n does not satisfy the recurrence relation.
2. Try T(n) = n:
- T(1) = 0
- T(2) = 1
- T(n) = n
- Now let's check if the recurrence holds:
T(n) = 2T(n-1) + T(n-2)
= 2(n-1) + (n-2)
= 2n - 2 + n - 2
= 3n - 4
We see that T(n) = 3n - 4, which is not equal to n. Therefore, T(n) = n does not satisfy the recurrence relation.
3. Try T(n) = \(n^2\):
T(1) = 0
T(2) = 1
T(n) = \(n^2\)
Now let's check if the recurrence holds:
T(n) = 2T(n-1) + T(n-2)
= \(2((n-1)^2) + (n-2)^2\)
= 2(\(n^2\) - 2n + 1) + (\(n^2\) - 4n + 4)
= 2\(n^2\) - 4n + 2 + \(n^2\) - 4n + 4
= 3\(n^2\) - 8n + 6
We see that T(n) = 3\(n^2\) - 8n + 6, which is not equal to \(n^2\). Therefore, T(n) = \(n^2\) does not satisfy the recurrence relation.
4. Prove the result formally using the substitution method:
Let's assume T(n) = \(n^p\) + c, where c is a constant offset and p > 0.
We substitute T(n) into the recurrence relation:
\(n^p + c = 2((n-1)^p + c) + ((n-2)^p + c)\)
Simplifying the equation, we get:
\(n^p + c = 2(n^p - pn^{(p-1)} + c) + (n^p - 2pn^{(p-1)} + 2^p + c)\)
Combining like terms, we have:
\(n^p + c = 2n^p - 2pn^{(p-1)} + 2^p + 3c\)
Rearranging the terms, we get:
\(pn^{(p-1)} = n^p - 3c + 2^p\)
Dividing both sides by n^(p-1), we have:
\(p = n - 3c/n^{(p-1)} + 2^p/n^{(p-1)}\)
As n approaches infinity, the right side of the equation tends to 0.
Therefore, for the equation to hold, p must be greater than 0 and c can be any real number.
In summary, none of the functions T(n) = n, T(n) = n, and T(n) = \(n^2\) satisfy the given recurrence relation T(n). However, by assuming T(n) = \(n^p\) + c, where p > 0 and c is a constant offset, we can derive the conditions for p and c that satisfy the recurrence relation.
Learn more about recurrence relation: https://brainly.com/question/29499649
#SPJ11
un ciclista recorre una pista de 800 metros en 1/4 de minuto, determina su rapidez
Answers
Answer:
3200 m/min = 192 km/h
Step-by-step explanation:
velocidad = distancia/tiempo
velocidad = (800 m)/(0.25 minutos)
velocidad = 3200 m/min × (1 km)/(1000 m) × (60 min)/(1 hr) = 192 km/h
Find the value of x
A.)25
B.)140
C.)5
D.)1

Answers
Answer:
25 = x
Step-by-step explanation:
The angles are vertical angles and vertical angles are equal
5x+15 = 6x -10
Subtract 5x from each side
5x-5x+15 = 6x-5x -10
15 = x - 10
Add 10 to each side
15+10 = x-10+10
25 = x
(5x+15)=(6x-10)
-6x. -6x
(-x+15)=-10
-15. -15
-x=-10
a sweetseller has 42 khajoor burfi and 26 badam burfi. he wants to stack them in such a way that each stack has the same amount and they take up the least area of the tray. what is the number that can be placed for in for each of this purpose ?
Answers
The burfi can be stacked in groups of 2, and arrange them in a rectangle with a length of 21 and a width of 13 to take up the least area of the tray
The number that can be placed for in for each of this purposeTo stack the khajoor burfi and badam burfi in such a way that each stack has the same amount, we need to find the greatest common divisor (GCD) of 42 and 26.
We can use the Euclidean algorithm to find the GCD:
42 = 26 x 1 + 16
26 = 16 x 1 + 10
16 = 10 x 1 + 6
10 = 6 x 1 + 4
6 = 4 x 1 + 2
4 = 2 x 2 + 0
The last non-zero remainder is 2, so the GCD of 42 and 26 is 2. Therefore, we can stack the burfi in groups of 2.
To find the number of stacks for each type of burfi, we divide the total number of burfi by the number in each stack:
Number of stacks of khajoor burfi = 42 / 2 = 21
Number of stacks of badam burfi = 26 / 2 = 13
To take up the least area of the tray, we want to stack the burfi in a rectangular shape. We can arrange the stacks in a rectangle with the length equal to the number of stacks of khajoor burfi and the width equal to the number of stacks of badam burfi:
Length = 21
Width = 13
So, we can stack the burfi in groups of 2, and arrange them in a rectangle with a length of 21 and a width of 13 to take up the least area of the tray
Learn more about greatest common divisor at https://brainly.com/question/219464
#SPJ1
PLZZZ hury and answer this thanks to whoever does

Answers
Answer:
3,264
Step-by-step explanation:
You have to use the straight line in the middle of the triangle as the height, the 12 below it as length, and the 34 on the side as width. And I must say, this prism is quite WIDE
Answer:
3264
Step-by-step explanation:
This is the answer.
Fact: A cow-bison hybrid is called a “beefalo”
cow
Answers
Answer:
yep
Step-by-step explanation:
thats true I think
define at least three (3) sources of experimental uncertainties for the experiments and explain specifically how each would have affected the accuracy of the data.
Answers
By identifying and minimizing these uncertainties, it is possible to improve the accuracy of the data and obtain more reliable results.
Experimental uncertainties refer to the errors or variations that may occur in the process of conducting an experiment. There are several sources of experimental uncertainties that can affect the accuracy of the data, specifically:
1. Instrument uncertainties: These uncertainties arise from the limitations of the instruments used in the experiment. For example, if a measuring device has a limited resolution or if it is not properly calibrated, it can lead to inaccuracies in the measurements.
2. Operator uncertainties: These uncertainties arise from the variations in the way different people conduct the experiment. For example, if different people are measuring the same quantity, they may have different techniques, which can lead to variations in the measurements.
3. Environmental uncertainties: These uncertainties arise from the variations in the environment in which the experiment is conducted. For example, if the temperature or pressure of the environment changes during the experiment, it can affect the measurements.
Each of these sources of experimental uncertainties can affect the accuracy of the data by introducing errors or variations in the measurements. By identifying and minimizing these uncertainties, it is possible to improve the accuracy of the data and obtain more reliable results.
Learn more about Uncertainties
brainly.com/question/14889571
#SPJ11
Write the equation for g (x)

Answers
The equation for g(x) passing through the point (3, 8) and with a slope of 25 is y - 8 = 25(x-3)
Equation of a lineThe equation of a line in point slope form is expressed as:
y - y1 = m(x-x1)
where:
m is the slope(x1, y1) is the point on the slopeIf the function g(x) is parallel to f(x), they will have the same slope. Hence the required slope is25.
Determine the required equation of a line
y - y1 = m(x-x1)
y - 8 = 25(x-3)
Hence the equation for g(x) passing through the point (3, 8) and with a slope of 25 is y - 8 = 25(x-3)
Learn more on equation of a line here: https://brainly.com/question/13763238
#SPJ1
answer. ill give brainliest to whoever answers first correctly

Answers
Answer:
∠ W = 30°
Step-by-step explanation:
using the cosine ratio in the right triangle
cos W = \(\frac{adjacent}{hypotenuse}\) = \(\frac{WY}{WX}\) = \(\frac{2\sqrt{21} }{4\sqrt{7} }\) = \(\frac{1}{2}\) \(\sqrt{\frac{21}{7} }\) = \(\frac{\sqrt{3} }{2}\) , then
∠ W = \(cos^{-1}\) ( \(\frac{\sqrt{3} }{2}\) ) = 30°
Solve x-4<3 graph the solution
Answers
Answer:
x<7
Step-by-step explanation:
move coefficeint and put it on inequality graph
Answer:
it should have an open circle on 7 and an arrow going to the left
Step-by-step explanation:
hope this helps
Plot the image of Point Q under the translation (x,y) (x-3, y + 4)

Answers
Answer:
(0, 3)
Step-by-step explanation:
Subtract 3 units from the X-coordinate
Add 4 units from the Y-coordinate
Solve the inequality for x.
8x-30< -5 (4- 2x)
_

Answers
Answer:
x > _ -5
Step-by-step explanation:
If you have any questions about the way I solved it, don't hesitate to ask me in the comments below =)

find the radian measure of an angle at the center of a circle with radius 77.0 cm that intercepts an arc length of 128 cm
Answers
The radian measure of the angle at the center of the circle is approximately 1.6623 radians.
We are given that the radius of the circle is 77.0 cm and the length of the intercepted arc is 128 cm. We need to find the radian measure of the angle at the center of the circle.
To solve this problem, we use the formula relating the angle at the center of a circle, the radius of the circle, and the arc length intercepted by the angle.
The formula is given byθ = s/rwhereθ = angle at the center of the circle in radians s = arc length intercepted by the angle r = radius of the circle Substituting the given values, we getθ = 128/77.0 = 1.6623 radians (rounded to four decimal places)
Therefore, the radian measure of the angle at the center of the circle is approximately 1.6623 radians.
For more such questions on radian measure
https://brainly.com/question/19758686
#SPJ8
For the function f(x) = x^4 - 5x^3find intervals where f(x) is increasing or decreasing, points of local maxima and minima of f(x), intervals where f(x) is concave up or concave down. the inflection points of f(x).Use a comma to separate points. Enter 'NONE if there are none.a. Interval (s) where f(x) is increasing: b. Interval (s) where f(x) is decreasing:c. Point(s) of local maxima of f(x):d. Point(s) of local minima of f(x)
Answers
Given:
\(f(x)=x^4-5x^3\)Aim:
We need to find intervals where f(x) is increasing or decreasing, points of local maxima and minima of f(x), and intervals where f(x) is concave up or concave down. the inflection points of f(x).
Explanation:
Differentiate the given function with respect to x to find the interval of increasing and decreasing.
\(f^{\prime}(x)=4x^3-5\times3x^2\)\(f^{\prime}(x)=4x^3-15x^2\)\(Let\text{ }\times f^{\prime}(x)=0\text{ to find a critical point.}\)\(4x^3-15x^2=0\)\(x^2(4x-15)=0\)\(x=0\text{ and 4x-15=0}\)\(x=0\text{ and x=}\frac{15}{4}.\)We find the following values for the variation chart.
\(-\infty<-1<0\)\(f^{\prime}(-1)=4(-1)^3-15(-1)^2=-19=negative\)\(-1<1<\frac{15}{4}\)\(f^{\prime}(1)=4(1)^3-15(1)^2=-11=negative\)\(\frac{15}{4}<4<\infty\)\(f^{\prime}(4)=4(4)^3-15(4)^2=16=positive\)Consider the variation chart.
a)
\(\text{ The interval of increasing is x}\in(\frac{15}{4},\infty).\)b)
\(\text{ The interval of decreasing is x}\in(-\infty,\frac{15}{4})\)
Which statements are true regarding quadrilateral ABCD? Check all that apply. ABCD has congruent diagonals. ABCD is a rhombus. ABCD is not a rectangle. ABCD is not a parallelogram. ABCD has four congruent angles
Answers
Answer:
ABCD has congruent diagonals.
ABCD is a rhombus.
ABCD has four congruent angles
Step-by-step explanation:
The following statements would be considered true
1. The quadrilateral ABCD could have the congruent diagonals as the diagonals are perpendicular
2. ABCD would be treated as the rhombus as it is a regular quadrilateral
3. ANd, It Have the four congruent angles that means the four angles be 90 degrees
The other statements would be false.

Answer:
A,B,E
Step-by-step explanation:
Edge 2021
6. (10 points) Construct an algebraic proof for the given statement. For all sets A, and B, (AUB) - Bº = A – B./
Answers
We have shown that (A ∪ B) - B' = A - B for any sets A and B.
To prove that (A ∪ B) - B' = A - B, we need to show that any element in the left-hand side is also in the right-hand side and vice versa.
First, let's consider an arbitrary element x in (A ∪ B) - B'. This means that x is in the union of A and B, but not in the complement of B. Therefore, x is either in A or in B, but not in B'. If x is in A, then x is also in A - B because it is not in B. If x is in B, then it cannot be in B' and thus is also in A - B. Hence, we have shown that any element in the left-hand side is also in the right-hand side.
Now, let's consider an arbitrary element y in A - B. This means that y is in A, but not in B. Since y is in A, it is also in (A ∪ B). Moreover, since y is not in B, it is not in B' and thus also in (A ∪ B) - B'. Therefore, we have shown that any element in the right-hand side is also in the left-hand side.
Thus, we have shown that (A ∪ B) - B' = A - B for any sets A and B.
To learn more about consider visit:
https://brainly.com/question/28144663
#SPJ11
How do I determine maximal velocity from the acceleration vs time graph?
Answers
To determine the maximal velocity from an acceleration vs. time graph, you need to follow these steps:
Identify the time interval during which the acceleration remains constant or nearly constant. This interval can be identified as a straight line on the graph.
Calculate the acceleration value during this interval by finding the slope of the line. The slope is the change in acceleration divided by the change in time.
Use the acceleration value and the time interval to calculate the change in velocity during this interval using the formula:
Δv = aΔt
Where Δv is the change in velocity, a is the acceleration, and Δt is the time interval.
Add the change in velocity to the initial velocity at the start of the time interval to obtain the maximal velocity. If the initial velocity was zero, then the maximal velocity will be equal to the change in velocity.
vmax = vi + Δv
Where vmax is the maximal velocity and vi is the initial velocity.
Note that this method assumes that the acceleration is constant or nearly constant during the time interval of interest. If the acceleration changes significantly during this time interval, you will need to break it down into smaller intervals and repeat the above steps for each interval to determine the maximal velocity.
Know more about maximal velocity here:
https://brainly.com/question/30505958
#SPJ11
what is the probability that at least seven customers arrive in three minutes, given that exactly two arrive in the first minute?
Answers
the probability that at least seven customers arrive in three minutes, given that exactly two arrive in the first minute, is approximately 0.081 or 8.1%.
How to solve?
To solve this problem, we can use the Poisson distribution, which models the probability of a certain number of events occurring in a fixed interval of time or space, given the expected rate of occurrence.
Let lambda be the expected rate of customer arrivals per minute. If exactly two customers arrive in the first minute, then the expected number of customers to arrive in three minutes is lambda ×3. We can use this expected value to calculate the probability of at least seven customers arriving in three minutes:
P(X ≥ 7 | X ~ ∝(λ×3))
= 1 - P(X ≤ 6 | X ~ ∝(λ×3))
= 1 - ∑[k=0 to 6] (e²(-λ3) ×(lλ3)²k / k!)
where e is the mathematical constant approximately equal to 2.71828, and k! denotes the factorial of k.
To find lambda, we can use the fact that exactly two customers arrive in the first minute. The Poisson distribution assumes that the number of events in a fixed interval of time or space follows a Poisson distribution with parameter lambda, which represents the expected rate of occurrence. Therefore, lambda is equal to the number of customers arriving per minute, which is 2.
Substituting lambda = 2 into the formula, we get:
P(X ≥ 7 | X ~ ∝(2×3))
= 1 - P(X ≤ 6 | X ~ ∝(6))
= 1 - ∑[k=0 to 6] (e²(-6) ×6²k / k!)
Using a calculator or computer software, we can evaluate this expression to get:
P(X ≥ 7 | X ~ ∝(6)) ≈ 0.081
Therefore, the probability that at least seven customers arrive in three minutes, given that exactly two arrive in the first minute, is approximately 0.081 or 8.1%.
To know more about Probability related question visit:
https://brainly.com/question/30034780
#SPJ1
The table shows the number of votes for different instruments. Select all of the reasons why a bar graph is an appropriate data display for the given data.
Instrument Drums Guitar Piano Saxophone
Number of
Votes
125
215 45
75

Answers
As we can see here in the table that the given set of data is categorized, we can use the bar graph to display the data.
Define a bar graph?The heights of the rectangular bars in a bar graph, which displays complete data, are proportionate to the values they indicate. The graph's bars can be displayed either vertically or horizontally. Bar graphs, commonly referred to as bar charts, are visual representations of groups of data. It is one method of processing data. A bar graph is a great tool for representing data that are unrelated to one another and do not need to be displayed in any particular sequence. The bars provide a visual representation for comparing amounts in several categories. Together with the title, labels, and scale range, bar graphs have two axes that are horizontal and vertical and are also known as the x and y axes.
As we can see here in the table that the given set of data is categorized, we can use the bar graph to display the data.
And to why we use a bar graph here:
Comparisons between various variables are simple and practical.
The least amount of work is required to prepare this diagram.
It is the most popular technique for representing data. As a result, it is utilised by numerous industries.
Data sets are compared using it. There is no interdependence between data sets.
Long-term patterns can be studied with its aid.
To know more about bar graphs, visit:
https://brainly.com/question/31158559
#SPJ1
