PLZZZZZZZZZZZZZZZZZZZZZZ HELP!!!
QUESTION: -2(x-6)=8
STUDENT WORK:
-2(x-6)=8
-2x-12=8
-12 -12
-2x+0=-4
-2x=-4
÷2 ÷2
x=-2
1. Explanation of Errors Made
2. Correct Solution (show all work)
Answers
Answer:
The error was made in the division step it should have been divided by negative 2
-2(x-6)=8
-2x+12=8
-2x=-4
-x=-2
X=2
Related Questions
is this the correct answer?

Answers
Answer:
yess it's right .
y=6+3x
Grade 6 - End of term assessment
Question 7
A seamstress needs to cut 15-inch pieces of ribbon from a roll of ribbon that is
9 feet in length. What is the greatest number of 15-inch pieces the seamstress
can cut from 5 of these rolls of ribbon?
Show your work.
Answers
Answer:
The greatest number of 15 inches pieces that can be cut from 5 rolls of length 9 feet is: 35
Step-by-step explanation:
Given
Total length of one roll of ribbon = 9 feet
As the pieces have to be cut into inches, we will convert the measurement in feet to inches
As there are 12 inches in one feet, 9 feet will be equal to:
9*12 = 108 inches
Now first of all, we have to see how many 15 inches pieces can be cut from one role
So,
\(=\frac{Length\ of\ roll}{Length\ of\ piece}\\=\frac{108}{15}\\=7.2\)
So the seamstress can cut 7 15-inch long pieces from a roll.
Now given that he has to cut from 5 rolls, the total number of 15-inch pieces will be:
\(= 5 * 7 =35\)
Hence,
The greatest number of 15 inches pieces that can be cut from 5 rolls of length 9 feet is: 35
QUESTION DOWN BELOW
PLEASE HELP EXPLAIN THIS

Answers
The surface area of a similar cylinder with a diameter 3 cm is 8.4375π cm².
What are similar figures?If two figures have the same shape, they are said to be comparable. In more formal terms, two figures are said to be similar if their respective angles are congruent and their corresponding side length ratios are identical.
Given a cylinder with a diameter 8 cm and a surface area 60π cm²
let the radius be R = dia/2 = 8/2= 4 cm
and let the height be H
total surface area of cylinder = 2πR(H + R)
60π = 2π(4)(4 + H)
4 + H = 60/8
H = 7.5 - 4
h = 3.5 cm
and a cylinder is similar to given cylinder,
let radius be r and height be h
given dia = 3 cm
r = 3/2 = 1.5 cm
since both cylinders are similar so the ratio of their height to radius is equal,
R/H = r/h
h = Hr/R
h = (3.5)(1.5)/4
h = 1.3125 cm
total surface area of cylinder = 2πr(h + r)
total surface area of cylinder = 2π(1.5)(1.5 + 1.3125)
the total surface area of the cylinder = 8.4375π cm²
Hence the area of a cylinder is 8.4375π cm².
Learn more about similar figures;
https://brainly.com/question/20368229
#SPJ1
Given the exponential function f (x) and the logarithmic function g(x), which of the following statements is true?
a. As x→∞, f (x)→∞ and g(x)→∞.
b. As x→∞, f (x)→∞ and g(x)→1.
c. As x→∞, f (x)→3 and g(x)→1.
d. As x→∞, f (x)→3 and g(x)→∞.
HELP!!! ASAP!!! PRE-CALCULUS!!!

Answers
Answer:
a
Step-by-step explanation:
Both the exponential and logarithmic functions tend to infinity.
According to Wine-Searcher, wine critics generally use a wine-scoring scale to communicate their opinions on the relative quality of wines. Wine scores range from to , with a score of indicating a great wine, indicating an outstanding wine, indicating a very good wine, indicating a good wine, indicating a mediocre wine, and below indicating that the wine is not recommended. Random ratings of a pinot noir recently produced by a newly established vineyard in follow:
87 91 86 82 72 91
60 77 80 79 83 96
Required:
a. Develop a point estimate of mean wine score for this pinot noir (to decimals).
b. Develop a point estimate of the standard deviation for wine scores received by this pinot noir (to decimals).
Answers
Answer:
a
\(\= x = 82 \)
b
\(s = 9.64 \)
Step-by-step explanation:
From the question we are told that
The data is 87 91 86 82 72 91 60 77 80 79 83 96
Generally the point estimate for the mean is mathematically represented as
\(\= x = \frac{\sum x_i }{n}\)
=> \(\= x = \frac{87 +91 + 86 + \cdots + 96}{12}\)
=> \(\= x = 82 \)
Generally the point estimate for the standard deviation is mathematically represented as
\(s = \sqrt{\frac{ \sum ( x_i - \= x )^2 }{ n -1 } }\)
=> \(s = \sqrt{\frac{ ( 87 - 82 )^2 +( 91 - 82 )^2 + \cdots + ( 96 - 82 )^2 }{ 12 -1 } }\)
=> \(s = 9.64 \)
Part(a): The required mean is 82
Part(b): The required standard deviation is 9.639
Mean:
The mean is one of the measures of central tendency.
Part(a):
The formula for finding the mean is,
\(\bar{x}=\frac{\sum x_i}{n}\)
Now, calculating the mean for the \(n=12\) observation
\(\bar{x}=\frac{87+91+86+82+72+91+60+77+80+79+83+96}{12}\\ \bar{x}=82\)
Part(b):
The formula for the standard deviation is,
\(S=\sqrt{\frac{\sum (x_i-\bar{x})^2}{n-1} }\)
Substituting the given values into the above formula we get,
\(S=\sqrt{\frac{((87-82)^2+(91-82)^2)+(86-82)^2+(82-82)^2+(72-82)^2+(91-82)^2+(60-82)^2+(77-82)^2+...+(96-82)^2}{12-1} } \\S=9.639\)
Learn more about the topic Mean:
https://brainly.com/question/11853639
Out of 20 people how many would you expect to say that they like all seasons
Answers
Answer:
None
Step-by-step explanation:
Truly, I'm not sure what type of problem this is, but most people don't favor all the seasons. If there is more to the problem, I would be glad to help further.
Answer:
One possible way to estimate how many people out of 20 would say that they like all seasons is to use a simple random sample. A simple random sample is a subset of a population that is selected in such a way that every member of the population has an equal chance of being included. For example, one could use a random number generator to assign a number from 1 to 20 to each person in the population, and then select the first 20 numbers that appear. The sample would then consist of the people who have those numbers.
Using a simple random sample, one could ask each person in the sample whether they like all seasons or not, and then calculate the proportion of positive responses. This proportion is an estimate of the true proportion of people in the population who like all seasons. However, this estimate is not exact, and it may vary depending on the sample that is selected. To measure the uncertainty of the estimate, one could use a confidence interval. A confidence interval is a range of values that is likely to contain the true proportion with a certain level of confidence. For example, a 95% confidence interval means that if the sampling procedure was repeated many times, 95% of the intervals would contain the true proportion.
One way to construct a confidence interval for a proportion is to use the formula:
p ± z * sqrt(p * (1 - p) / n)
where p is the sample proportion, z is a critical value that depends on the level of confidence, and n is the sample size. For a 95% confidence interval, z is approximately 1.96. For example, if out of 20 people in the sample, 12 said that they like all seasons, then the sample proportion is 0.6, and the confidence interval is:
0.6 ± 1.96 * sqrt(0.6 * (1 - 0.6) / 20)
which simplifies to:
0.6 ± 0.22
or:
(0.38, 0.82)
This means that we are 95% confident that the true proportion of people who like all seasons in the population is between 0.38 and 0.82. Therefore, based on this sample and this confidence interval, we would expect between 8 and 16 people out of 20 to say that they like all seasons in the population.
MARK AS BRAINLIEST!!!
1. Global warming creates local problems. Projections forecast that even a moderate air temperature increase of only 1.8 °F could cause brook trout distributions to decrease dramatically. For example, such a temperature increase would take Washburn county's 19 ponds that support brook trout down to 10 ponds. What would be the percent decrease in the number of ponds that support brook trout?
Answers
The percent decrease in the number of ponds that support brook trout would be approximately 47.37%.
To calculate the percent decrease in the number of ponds that support brook trout, we need to determine the difference between the initial number of ponds and the final number of ponds, and then express that difference as a percentage of the initial number of ponds.
Initial number of ponds: 19
Final number of ponds: 10
To calculate the percent decrease, we can use the following formula:
Percent Decrease = (Difference / Initial Value) * 100
Let's apply this formula to the given data:
Difference = Initial number of ponds - Final number of ponds
Difference = 19 - 10
Difference = 9
Percent Decrease = (9 / 19) * 100
Now, let's calculate the percent decrease:
Percent Decrease = (9 / 19) * 100
Percent Decrease ≈ 47.37%
For such more question on number:
https://brainly.com/question/30752681
#SPJ8
Kai and Finley were studying together for their exams the
following day. They had planned to spend the entire two days
after the exams hiking to a log cabin on the Winslow trail. The trail
was closed on Mondays, Wednesdays, and weekends.
On which day of the week was their exam scheduled?
Answers
Their exam must have been scheduled on Wednesday, allowing them to start hiking on Thursday after the exams.
How to determine which day of the week was their exam scheduledTo determine the day of the week on which Kai and Finley's exam was scheduled, we need to consider the information provided about the trail being closed on Mondays, Wednesdays, and weekends.
If they had planned to hike to the log cabin for two days after the exams, and the trail is closed on weekends, it means they cannot start hiking on Saturday or Sunday.
Since they cannot start hiking on Saturday or Sunday, the two possible options for the exam day would be Monday or Wednesday, as they have not specified whether the hike starts immediately after the exams or the day after.
However, we can conclude that their exam was not scheduled on Monday, as the trail is closed on Mondays, and they had planned to hike immediately after the exams.
Therefore, their exam must have been scheduled on Wednesday, allowing them to start hiking on Thursday after the exams.
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
Which property is shown below?
5 + 2y + 3z = 5+ 3z + 2y
A. Commutative Property of Addition
B. Additive Identity Property
C. Associative Property of Addition
D. Additive Inverse Property
Answers
Answer:
C
Step-by-step explanation:
5+2y+3z=5+3z+2yA
Intercambie los lados para que todos los términos de las variables estén en el lado izquierdo.
5+3z+2yA=5+2y+3z
Resta 5 en los dos lados.
3z+2yA=5+2y+3z−5
Resta 5 de 5 para obtener 0.
3z+2yA=2y+3z
Resta 3z en los dos lados.
2yA=2y+3z−3z
Combina 3z y −3z para obtener 0.
2yA=2y
Anula 2 en ambos lados.
yA=y
Divide los dos lados por y.
y
yA
=
y
y
Al dividir por y, se deshace la multiplicación por y.
A=
y
y
Divide y por y.
A=1
Arianys is going to invest $11,000 and leave it in an account for 9
years. Assuming the interest is compounded monthly, what interest
rate, to the nearest hundredth of a percent, would be required in order
for Arianys to end up with $20,000?
Answers
The compound interest rate of the investment is 1.10%
How to determine the compound interest rate?The given parameters about the compound interest are
Principal, P = $11,000
Amount, A = $20,000
Time, t = 9
Number of times, n = 12 i.e. monthly interest
To calculate the amount, we have:
A = P(1 + R/n)^nt
Substitute the known values in the above equation, so, we have the following representation
20000 = 11000 * (1 + r/12)^(12 * 9)
This gives
1.82 = (1 + r/12)^108
Take the 108th root of both sides
1 + r/2 = 1.0055
Subtract 1 from both sides
r/2 = 0.0055
Multiply by 2
r = 0.011
Express as percentage
r = 1.10%
Hence, the value of the interest rate is 1.10%
Read more about compound interest at:
https://brainly.com/question/2455673
#SPJ1
Answer:
6.66%
Step-by-step explanation:
Compounded Monthly:
�
=
�
(
1
+
�
�
)
�
�
A=P(1+
n
r
)
nt
Compound interest formula
�
=
20000
�
=
11000
�
=
9
�
=
12
A=20000P=11000t=9n=12
Given values
20000
=
20000=
11000
(
1
+
�
12
)
12
(
9
)
11000(1+
12
r
)
12(9)
Plug in values
20000
=
20000=
11000
(
1
+
�
12
)
108
11000(1+
12
r
)
108
Multiply
20000
11000
=
11000
20000
=
11000
(
1
+
�
12
)
108
11000
11000
11000(1+
12
r
)
108
Divide by 11000
1.8181818
=
1.8181818=
(
1
+
�
12
)
108
(1+
12
r
)
108
(
1.8181818
)
1
/
108
=
(1.8181818)
1/108
=
[
(
1
+
�
12
)
108
]
1
/
108
[(1+
12
r
)
108
]
1/108
Raise both sides to 1/108 power
1.0055509
=
1.0055509=
1
+
�
12
1+
12
r
−
1
−1=
−
1
−1
Subtract 1
0.0055509
=
0.0055509=
�
12
12
r
12
(
0.0055509
)
=
12(0.0055509)=
(
�
12
)
12
(
12
r
)12
Multiply by 12
0.0666108
=
0.0666108=
�
r
6.66108
%
=
6.66108%=
�
r
Convert to percent (multiply by 100)
�
≈
r≈
6.66
%
6.66%
Round to the nearest hundredth of a percent
What is the length of EF in the right triangle below?
D
26
10
E
F
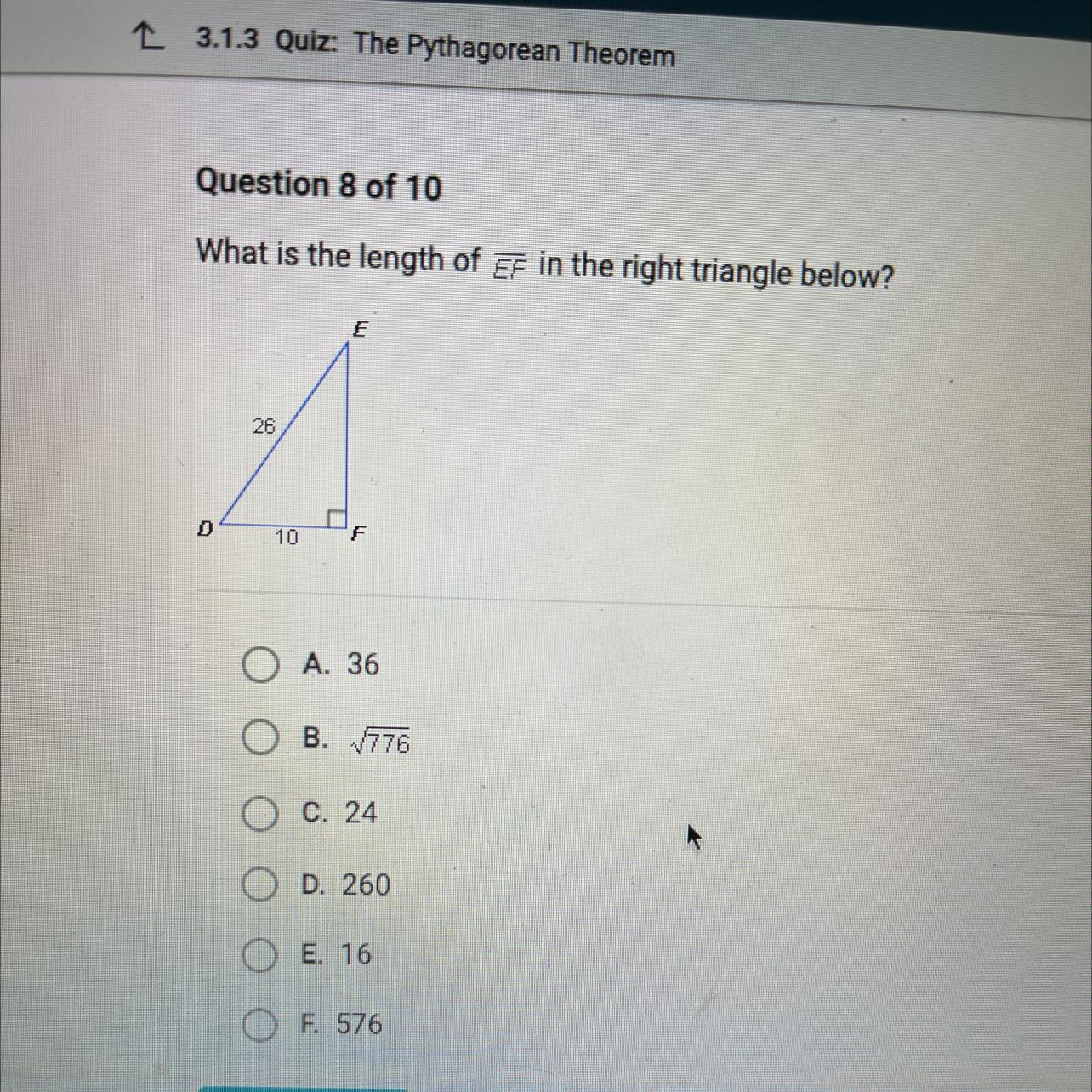
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
find the perimeter of a triangle where one side is 2 inches, one side is 6 inches and another side is 10 inches.
(a) 2in.
(b) 9in.
(c) 36in.
(d) 18in.
Answers
Answer:
(d) 18 in.
Step-by-step explanation:
When we're given the three sides of a triangle, one formula we can use for perimeter of a triangle is:
P = s1 + s2 + s3, where
P is the perimeter,and s1, s2, and s3 are the three sides:P = 2 + 6 + 10
P = 8 + 10
P = 18
Thus, the perimeter of the triangle is 18 in.
What is the volume of this figure?
Enter your answer in the box.
yd³

Answers
The volume of the composite figure is
4095 cubic ydHow to find the volume of the composite figureThe volume is calculated by dividing the figure into simpler shapes. and adding the individual volumes
The simple shapes used here include
trapezoid andrectangleVolume of rectangle = length x width x depth
= 30 * 9 * 7
= 1890 cubic yd
Volume of trapezoid = 1/2 (sum of parallel lines) x height x depth
= 1/2 (30 + 19) x 10 x 9
= 2205 cubic yd
Total volume
= 1890 cubic yd + 2205 cubic yd
= 4095 cubic yd
Learn more about composite shapes at
https://brainly.com/question/8370446
#SPJ1
please help me thanks

Answers
Answer:
1/14
Step-by-step explanation:
Which is the equation of the line, in point-slope form, that has a slope of 5 and passes through the point (-2, 4)?
y − 4 = 5(x−2)
y − 2 = 5(x+2)
y − 2 = −5(x−4)
y − 4 = 5(x+2)
Answers
\((\stackrel{x_1}{-2}~,~\stackrel{y_1}{4})\qquad \qquad \stackrel{slope}{m}\implies 5 \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{5}(x-\stackrel{x_1}{(-2)})\implies y-4=5(x+2)\)
Juan buys candy that costs $8 per pound. He will spend at least $48 on candy. What are the possible numbers of pounds he will buy?
Use p for the number of pounds Juan will buy.
Write your answer as an inequality solved for p.
Answers
In a case whereby Juan buys candy that costs $8 per pound and will spend at least $48 on candy the possible numbers of pounds he will buy written in inequality is is p>5 (at least 5 pounds).
How can these number be determined?Inequality in math refers to a statement that one quantity is either greater than, less than, or not equal to another quantity. Inequalities are often represented using symbols such as "<" (less than), ">" (greater than), or "≤" (less than or equal to) and "≥" (greater than or equal to). For example, the inequality "x > 3" states that the variable "x" is greater than the value of 3. The inequality "y ≤ 5" means that the variable "y" is less than or equal to 5.
From the question, p = number of pounds Juan will buy.
candy=costs $8 per pound
$20/$4 = 5 pounds
p>5
at least 5 pounds
Learn more about costs at:
https://brainly.com/question/25109150
#SPJ1
Need some help with this one.

Answers
Answer:
Cylinder A: 3.58 m^3, cylinder B: 8.72 m^3, cylinder B has the greater volume
Step-by-step explanation:
Volume of a cylinder \(V=\pi r^2h\) r is the radius, h is the height.
Cylinder A: The circumference is given, C = 3. Circumference is found by the formula \(C=2 \pi r\). Replace C with 3 and solve for r so it can be used in the volume formula.
\(3=2\pi r\\3=2(3.14)r\\3=6.28r\\r=3 \div 6.28 \approx .4777\)
Volume: \(V=(3.14)(.4777)^2(5) \approx 3.58\) cubic meters
Cylinder B:
\(C=2\pi r\\5=2(3.14)r\\r=5 \div 6.28 \approx .7962\\\\V=\pi r^2h\\ V=(3.14)(.7962)^2(3) \approx 8.72\) cubic meters
A sales person starts working 40 hours per week at a job with 2 options for being paid . Option A is an hourly wage of $19. Option B is a commission rate of 8% on weekly sales.
How much does the sales person need to sell in a given week to earn the same amount with each option?
A. $9,500
B. $4,750
C. $760
D. $320
Answers
Given, Option A: Hourly wage is $19 and the salesperson works 40 hours per week. So, he will earn in a week \(\sf = 19 \times 40 = \$760\)
Now, according to option b, he will get 8% commission on weekly sales.
Let. x = the amount of weekly sales.
To earn the same amount of option A, he will have to equal the 8% of x to $760
So, \(\sf \dfrac{8x}{100}=760\)
Or, \(\sf 8x= 76000\)
Or, \(\sf x= \dfrac{76000}{8}=9500\)
the salesman needs to make a weekly sales of $9,500 to earn the same amount with two options.
8. The probability that Ava gets promoted is 7/10. Find the odds in favor of Ava getting promoted.
Answers
let y1 and y2 are independent random variables that are both uniformly distributed on the interval (0,1). find p(y1 <1
Answers
the probability of y1 being less than 1 is 1, regardless of the actual value of y1. P(y1 < 1) = 1
Since y1 and y2 are both uniformly distributed on the interval (0,1), this means that all possible values of y1 and y2 are equally likely. Therefore, the probability of y1 being less than 1 is 1, since any value of y1 between 0 and 1 has the same probability of occurring. This means that the probability of y1 being less than 1 is 1.
Since y1 and y2 are both uniformly distributed on the interval (0,1), this means that all possible values of y1 and y2 between 0 and 1 are equally likely to occur. This means that the probability of y1 being less than 1 is the same as the probability of y1 being equal to any value between 0 and 1. Since this probability is the same for all possible values of y1, the probability of y1 being less than 1 is 1, regardless of the actual value of y1. This is because any value of y1 between 0 and 1 has the same probability of occurring, meaning that the probability of y1 being less than 1 is 1.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
Find the solution of the system of equations shown on the graph

Answers
Answer:
(-2, 4)
Step-by-step explanation:
The solution to the systems of equations shown on the graph is the point at which the lines of both equations intersect each other.
The solution is (-2, 4). That is, for both lines, when x = -2, y = 4.
PLEASE HELP true or false I WILL MAKE BRAINLIEST

Answers
Answer:
True
Step-by-step explanation:
They are the same dimensions
Answer:
I think its true because there both the same shape and dimension
g is a trigonometric function of the form � ( � ) = � cos ( � � + � ) + � g(x)=acos(bx+c)+dg, left parenthesis, x, right parenthesis, equals, a, cosine, left parenthesis, b, x, plus, c, right parenthesis, plus, d. Below is the graph of � ( � ) g(x)g, left parenthesis, x, right parenthesis. The function has a maximum point at ( 3.5 , − 4 ) (3.5,−4)left parenthesis, 3, point, 5, comma, minus, 4, right parenthesis and a minimum point at ( − 1 , − 5 ) (−1,−5)left parenthesis, minus, 1, comma, minus, 5, right parenthesis. Find a formula for � ( � ) g(x)g, left parenthesis, x, right parenthesis. Give an exact expression. � ( � ) = g(x)=g, left parenthesis, x, right parenthesis, equals A graph of a trigonometric wave on an x y coordinate plane. The x axis scales by two and the y axis scales by one. There is a point on the graph at the minimum at (negative one, negative five) and a point on the maximum next to the mentioned point at (three and one half, negative four).
Answers
The exact expression for g(x) is 2.25cos((2π/4.5)×(x-3.5)) - 4.
Describe Function?A function can be represented using a formula or an equation, and it can be graphed on a coordinate plane. The input values are typically represented on the x-axis and the output values on the y-axis.
From the given information, we know that the function g(x) has a maximum point at (3.5, -4) and a minimum point at (-1, -5).
The general form of a cosine function is f(x) = A×cos(Bx + C) + D, where A is the amplitude, B is the period, C is the phase shift, and D is the vertical shift.
Since the function has a maximum point at (3.5, -4), we know that the graph has been shifted to the left by 3.5 units. Therefore, we can write the function as g(x) = A×cos(B(x - 3.5)) + D.
Similarly, since the function has a minimum point at (-1, -5), we know that the graph has been shifted upwards by 1 unit. Therefore, we can write the function as g(x) = A×cos(B(x - 3.5)) - 4.
To determine A and B, we can use the fact that the period of the function is 4.5 units (the distance between the maximum and minimum points). Therefore, we have B = 2*pi/4.5.
To determine A, we can use the fact that the amplitude is half the distance between the maximum and minimum points, which is 0.5*(5-(-4)) = 4.5. Therefore, we have A = 4.5/2 = 2.25.
Substituting these values into the equation for g(x), we have:
g(x) = 2.25cos((2π/4.5)×(x-3.5)) - 4
Therefore, the exact expression for g(x) is:
g(x) = 2.25cos((2π/4.5)×(x-3.5)) - 4.
To know more about equation visit:
https://brainly.com/question/22964920
#SPJ1
What is the greatest common factor of 8,16,40
Answers
Step-by-step explanation:
To find the greatest common factor (GCF) of 8, 16, and 40, we can determine the largest number that evenly divides all three of them.
Let's first find the prime factorization of each number:
- 8 = 2 * 2 * 2
- 16 = 2 * 2 * 2 * 2
- 40 = 2 * 2 * 2 * 5
Now, let's identify the common factors by finding the minimum exponent for each prime factor:
- 2 is a common factor with an exponent of 2 (appearing twice in the prime factorization of 8 and 16).
- 5 is not a common factor since it appears only in the prime factorization of 40.
The GCF is obtained by multiplying the common factors with their respective minimum exponents:
GCF = 2^2 = 4
Therefore, the greatest common factor of 8, 16, and 40 is 4.
Plz help I don’t know what to do it and I need a explanation for it

Answers
Answer:
A function is defined as an equation in which no x value has two y values. You can find the answer to this via the vertical line test. If you move a pencil across a graph and it does not touch the graph at two points, then it is a function. Utilizing this logic, the correct answer is yes, this is a function.
Step-by-step explanation:
Plz help me thanks so muchhhhh

Answers
Hi there.
The answer is (-2,7). The second choice.
Explanation:
We can use the graph method or the solving method.
For the graph method, find where both graphs intercept and that is x = - 2 y = 7.
But if you don't use the graph method. We can solve the equation.
\(y = 0.5x+ 8 \\ y = \frac{5}{10} x + 8 \\ y = \frac{1}{2} x + 8\)
Convert the expressions in simplified form.
Then combine both equations.
\( \frac{1}{2}x + 8 = 5 - x\)
Because there is the denominator. We get rid of it.
Multiply the whole equation by 2.
\( \frac{1}{2} x(2) + 8(2) = 5(2) - x(2) \\ x + 16 = 10 - 2x \\ 3x = 10 - 16 \\ 3x = - 6 \\ x = - 2\)
Since it is the two variables linear equations, we need to find y-value too.
Substitute x = -2 in any given equations.
I will substitute x = -2 in y = 5-x
\(y = 5 - x \\ \)
Substitute x = -2 in the equation.
\(y = 5 - ( - 2) \\ y = 5 + 2 \\ y = 7\)
Thus, the answer is x = -2, y = 7
Or
(-2,7)
Find the coefficient of the given term when the expression is expanded by the binomial theorem.
x7 in (3x + 4)10
Can someone help me out with this problem i need step by step help
Discrete mathematics
Answers
The coefficient of \(x^{7}\) is 16796160.
For this, we have to find the coefficient of \(x^{7}\) in \((3x+4)^{10}\)
General Term: This term symbolizes all of the terms in the binomial expansion of (x + y)^n.
The general term in the binomial expansion of (x + y)^n is
T(r+1) = nCr x^(n-r)y^r.
Here the r-value is one less than the number of the term of the binomial expansion. Also, nCr is the coefficient, and the sum of the exponents of the variables x and y is equal to n.
We can use the general term for this.
\(T_{r+1} = (nCr) a^{n-r} x^{r}\)
Since we have to find \(x^{7}\),
\(T_{3+1} = (10C3)(3x)^{7} 4^{3} \\T_{3+1} = [(10C3)3^{7} 4^{3} ]x^{7}\)
This is the coefficients of \(x^{7}\)
Calculating,
10C3 = 120 (using combinations)
\(3^{7} = 2187\\4^{3} = 64\)
Therefore, multiplying the 3,
Coefficients of \(x^{7}\) = 120 * 2187 *64
= 16796160
To learn more about the binomial theorem, visit
brainly.com/question/27813780
#SPJ4
in the coordinate plane, ABCD has vertices with coordinates A(1,-1), B(-5,3), C(-3,6),
and D(3,2)
Answers
Answer:
C
Step-by-step explanation:
finding values of products and quotient functions
\(( \frac{r}{s} )(3) = \)
(3) = [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/fo6qtw13QDITrL0XHWTkFEFXENPGcfQd.jpeg)
Answers
The product and the quotient of the functions are as follows:
(rs)(4) =8
(r / s)(3) = 2
How to solve function?A function relates input and output. It relates an independent variable with a dependent variable.
Therefore, let's solve the function as follows:
r(x) = 2√x
s(x) = √x
Therefore, let's find
(rs)(4) = r(4) × s(4) = 2√4 × √4 = 4 × 2 = 8
Let's find
(r / s)(3) = r(3) / s(3) = 2√3 / √3 = 2
Therefore,
(rs)(4) =8
(r / s)(3) = 2
learn more on function here: https://brainly.com/question/17430065
#SPJ1
4. Which function has two
x-intercepts, one at
(5, 0) and one at (-4, 0)
f(x) = (x - 5)(x – 4)
f(x) = (x - 5)(x + 4)
f(x) = (x + 5)(x - 4)
f(x) = (x + 5)(x +4)
Answers
Answer: B) (x - 5)(x + 4)
Step-by-step explanation:
we’re looking for x intercepts at x = 5 and x = -4
x - 5 = 0; x = 5
x + 4 = 0; x = -4
(x - 5)(x + 4) is your answer