Put the following equation of a line into slope-intercept form, simplifying all fractions.
20x+4y=8
Answers
the answer for the given question is slope is -5 and y- intercept is 2.
The slope intercept form of a straight line is one of the most common ways to represent a line's equation. When given the slope of a straight line and the y-intercept, the slope intercept formula can be used to find the equation of a line (the y-coordinate of the point where the line intersects the y-axis).
The slope-intercept form is y = mx + b , where m is the slope and b is the y-intercept.
y = mx + b
Take 20x off both sides of the equation.
4y = 8 − 20x
Simplify each term by dividing it by 4y = 8 - 20x.
y = 2 − 5x
Reorder 2 and -5x.
y =−5x + 2
Therefore after simplification we get the slope as -5
and the y-intercept as 2
learn about slope intercept more here:
https://brainly.com/question/1884491
#SPJ9
Related Questions
In the tournament described in Exercise 11 of Section 2.4, a top player is defined to be one who either beats every other player or beats someone who beats the other player. Use the WOP to show that in every such tournament with n players n∈ N, there is at least one top player.
Answers
Using the Well-Ordering Principle (WOP), it can be proven that in every tournament with n players (where n is a natural number), there is at least one top player, defined as someone who either beats every other player or beats someone who beats the other player.
We will prove this statement by contradiction. Assume that there exists a tournament with n players where there is no top player. This means that for each player, there exists either another player who beats them or a chain of players such that each player beats the next one. Now, consider the set S of all players in this tournament. Since S is a non-empty set of natural numbers, it has a least element, let's say k.
Now, player k either beats every other player in the tournament, making them a top player, or there exists a player, let's say player m, who beats player k. In the latter case, we have a chain of players: k, m, p_1, p_2, ..., p_t, where p_1 beats p_2, p_2 beats p_3, and so on until p_t.
However, this contradicts the assumption that there is no top player, as either player k beats every other player (if m does not exist), or player m beats someone who beats the other player (if m exists). Hence, by contradiction, we have shown that in every tournament with n players, there is at least one top player.
Learn more about non-empty set here:
https://brainly.com/question/1581607
#SPJ11
Please help! Correct answer only, please! I need to finish this assignment this week. Determine the value of the following if it is possible. If it is not possible, explain.

Answers
Answer:
Option D is the correct answer
Step-by-step explanation:
Since, dimensions of both the matrices are different, hence they cannot be added.
The sum of two numbers is -18. If the first number is 10, which equation represents this situation, and what is the second number?
Answers
= -28
Step by step solved:
Let's assume that the second number is represented by the variable "x".
The sum of the first number (10) and the second number (x) is -18. We can represent this situation with the following equation:
10 + x = -18
To solve for "x", we can isolate the variable by subtracting 10 from both sides of the equation:
x = -18 - 10
Simplifying the right-hand side:
x = -28
Therefore, the second number is -28.
Find the average value of the function f(x) = (x + 2) on the interval [0, 3].
![Find the average value of the function f(x) = (x + 2) on the interval [0, 3].](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/P5zl0SIYRlJ5Lz5JinzKHjLeHoS5AWmn.png)
Answers
The average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Calculate the definite integral of the function over the interval [a, b], then divide it by the interval's length (b - a), in order to determine the average value of a function f(x) over the interval.
Given that the interval is [0, 3] and the function f(x) = (x + 2), we have:
= (1/3) × [1/2 x² + 2x] evaluated from x=0 to x=3
= (1/3) × [(1/2 × 3² + 2×3) - (1/20² + 20)]
= (1/3) × [(9/2 + 6) - 0]
= (1/3) × (21/2)
= 7/2
Therefore, the average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Learn more about definite integral click;
https://brainly.com/question/30760284
#SPJ1
determine whether the statement is true or false. if it is false, rewrite it as a true statement. a data set can have the same mean, median, and mode.
Answers
False. A data set can have the same mean and median, but not necessarily the same mode.
The mean, median, and mode are measures of central tendency used to describe a data set. The mean is the average of all the values in the data set, the median is the middle value when the data set is arranged in ascending or descending order, and the mode is the value that appears most frequently.
While it is possible for a data set to have the same mean and median, it is not necessary for the mode to be the same as well. For example, consider a data set with the values [1, 2, 3, 3, 4, 5]. In this case, the mean is 3, the median is 3, and the mode is also 3 because it appears twice, which is more frequently than any other value. However, there are scenarios where the mode can be different from the mean and median, such as in a bimodal distribution where there are two distinct peaks in the data set.
Learn more about data:
brainly.com/question/28285882
#SPJ11
Find value of X please

Answers
Answer:
x=7
Step-by-step explanation:
Step #1- Set the two lines equal to each other
10+12=x+15
Step #2- Solve for the line you have all values for
10+12=22
Step#3- Plug 22 back into the equation where the two lines are set equal to each other
22=x+15
Step #4- Solve for X algebraically
22=x+15
22-15=x
7=x
describe how would you dilate triangle ABC using center P and scale factor 3/2
Answers
The dilation of the triangle is illustrated below.
What is dilation?Resizing an object uses a transformation called dilation. Dilation is used to enlarge or contract the objects. The result of this transformation is an image that retains the original shape.
The image's size will depend on the scale factor, which is used to dilate a mathematical object. See the diagram below. We end up with a triangle where the sides are 3/2 = 1.5 times longer compared to the original diagram.
Because segment AC is going through P (center of dilation), this means that segment A'C' will also go through P. Furthermore, it means AC and A'C' overlap. However, as mentioned earlier, A'C' is 1.5 times longer than AC.
Another thing to note is that line BC is parallel to line B'C', and line AB is parallel to A'B'.
Learn more about triangles on:
https://brainly.com/question/17335144
#SPJ1

2000 a month for 15 months with 4% interest
Answers
Answer:
1200
Step-by-step explanation:
4% of 2000 is 80 then do 80*15 and you get 1200
Question 2 of 25
What value of cmakes the polynomial below a perfect square?
x + 10x+ c
CE
O A. 100
O B. 20
O C. 5
O D. 25
Answers
Answer:
25
Step-by-step explanation:
x^2 + 10x + 25 = (x+5)^2
Write 37341000000 in standard form.
Answers
Answer:
trinta e sete bilhões, trezentos e quarenta e um milhões.
4p5q3xp2q-4 simplify
Answers
The simplified form of the given expression is 4p⁷/q.
The given expression is 4p⁵q³×p²q⁻⁴.
Using the exponential law, aⁿ×aˣ=aⁿ⁺ˣ, we get
4(p⁵×p²)(q⁻⁴×q³)
= 4p⁵⁺²q⁻⁴⁺³
= 4p⁷q⁻¹
= 4p⁷/q
Therefore, the simplified form of the given expression is 4p⁷/q.
To learn more about an exponents visit:
https://brainly.com/question/15993626.
#SPJ1
please help asap !!!!!
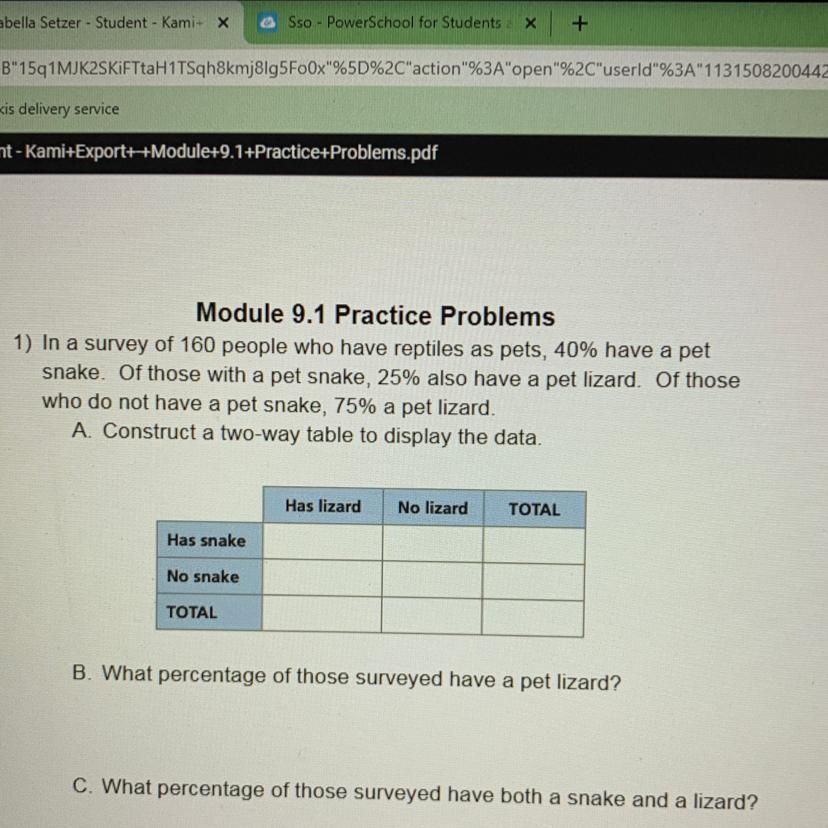
Answers
Answer:
Part A
The table is filled in based on given data.
Total = 160Snake = 160*0.4 = 64No snake = 160 - 64 = 96Snake and lizard = 64*0.25 = 16Snake no lizard = 64 - 16 = 48No snake lizard = 96*0.75 = 72No snake no lizard = 96 - 72 = 24See attached
Part B
88 out of 16088/160*100% = 55%Part C
16 out of 16016/160*100% = 10%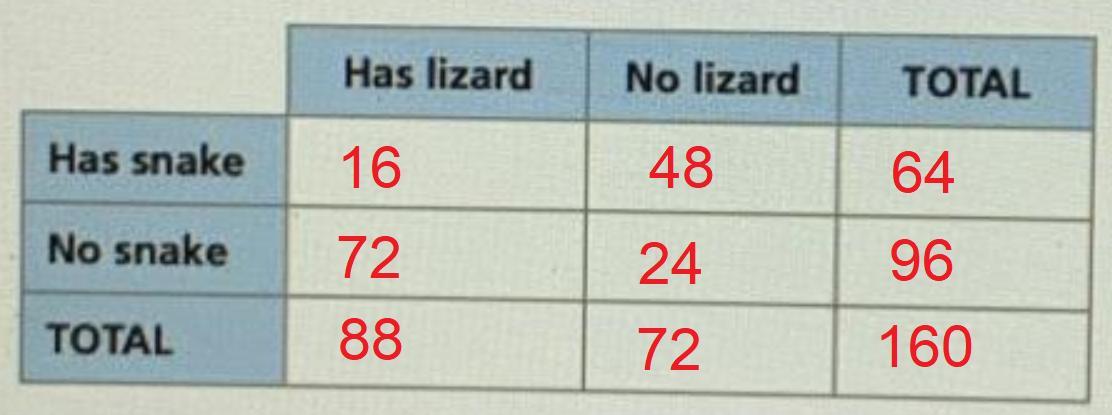
Find the area of the following
kite:
10 cm
4 cm
4 cm
4 cm
A = [?] cm2
![Find the area of the followingkite:10 cm4 cm4 cm4 cmA = [?] cm2](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/xoCes9KzydwgHGtSlK64J8col9rpcvPV.png)
Answers
Answer:
40
Step-by-step explanation:
hope it helps and sorry if it's wrong but i wish you luck
I need this by the end of the day may someone help me only have 13 points left

Answers
There are different ways a person can make up a story about a word problem. The square root of 81 - 7 is 2. Hence the story is given below.
What is the story of the word problem?The hypothetical story goes like this: Mia was trying to figure out the length of the missing side of a square garden bed. She knew that the total area of the garden bed was 81 square feet. She also knew that she had already planted in a section of the garden bed that was 7 feet wide.
So, what will be the length of the missing side of the garden bed if Mia wants to make sure it is completely filled with soil. In order to solve this problem, Mia used the equation: the square root of 81-7=2. She plugged in the values she knew and solved for the missing side length. Therefore, The solution will be:= ✓81 - 7= 9 - 7= 2
Learn more about Story writing on
https://brainly.com/question/30854821
#SPJ1
A story for the word problem is that what will be the length of the missing side of a square garden when the total area is 81 feet² and the width was 7 feet wide?
How to explain the square rootFrom the information, we are seeking a story problem that has the equation had the square root of 81 - 7 = 2.
This will be written as story for the word problem is that what will be the length of the missing side of a square garden when the total area is 81 feet ² and the width was 7 feet wide?
The length will be calculated thus :
= √ 81 - 7
= 9 - 7
= 2
The length of the missing side is 2 feet.
Learn more about square root on
https://brainly.com/question/428672
#SPJ1
in short bingo, a $5\times5$ card is filled by marking the middle square as wild and placing $24$ other numbers in the remaining $24$ squares. specifically a card is made by placing $5$ distinct numbers from the set $1-10$ in the first column, $5$ distinct numbers from $11-20$ in the second column, $4$ distinct numbers $21-30$ in the third column (skipping the wild square in the middle), $5$ distinct numbers from $31-40$ in the fourth column and $5$ distinct numbers from $41-50$ in the last column. one possible short bingo card is: to play short bingo, someone names numbers, chosen at random, and players mark those numbers on their cards. a player wins when he marks $5$ in a row, horizontally, vertically, or diagonally. how many distinct possibilities are there for the values in the first column of a short bingo card? (the placement on the card matters, so the order of the numbers matters, so $5~4~3~2~1$ is to be considered different from $1~2~3~4~5$, for instance.)
Answers
The number of distinct possibilities for the values in the first column of a short bingo card is = 10000
According to the data given in the question,
The middle square is contained with the word = WILD
Number of remaining squares = 24
Total number of choices given to an individual = 4
Number of options provided for each choice made = 10
Let N denote the number of choices,
In order to find the number of choices we will use the following formula,
N = \(Number of options^{Number of choices}\)
N = \(10^{4}\)
N = 10000
Therefore, the number of distinct possibilities for the values in the first column of a short bingo card is = 10000
To know more about Probability and this question,
https://brainly.com/question/28021875
#SPJ4

HEYYYY GUYYYSSS HELPP MEEE, ILL MARK YOU BRAINIEST. PLEEEAAASEEEE

Answers
Answer:
C = 100 + 40n
The independent variable is n (number of months) and the dependent variable is C ( total cost)
Step-by-step explanation:
Let the total cost of the fitness center = C
Given fixed cost = $100
given cost per month = $40
let number of month = n
The total cost of the fitness center in a given 'n' month is calculated as;
C = 100 + 40n
From the above equation;
the independent variable is n (number of months) and
the dependent variable is C ( total cost)
C = 100 + 40n The independent variable is n (number of months) and the dependent variable is C ( total cost)
which is the total length of both sides of the roof 4x

Answers
Answer:
b. 40m
Step-by-step explanation:
\(length \: of \: x \\ {x}^{2} = {8}^{2} + {6}^{2} \\ {x}^{2} = 64 + 36 \\ {x}^{2} = 100 \\ \sqrt{ {x}^{2} } = \sqrt{100} \\ x = 10m\)
\(x = 10m \\ 4x = 4 \times 10 \\ 4x = 40m\)
Which of the following is true?
Sine is negative in Quadrant I.
Tangent is positive in Quadrant III.
Cosine is positive in Quadrant III.
Sine is negative in Quadrant II.
Answers
B) Tangent is positive in Quadrant III is correct!
what is 100,000,000,000,000,00 x 368,900=?
Answers
Answer:
3.689e+20
Step-by-step explanation:
thats the answer
Micah is building a structure that requires 3 pieces of wood each measuring 834 feet and 4 pieces of wood each measuring 1058 feet. What is the total length of wood, in feet, that Micah needs?
Answers
Answer:
834*3 + 1058*4 = ___
2,502 + 4,232 = 6,734 feet of wood
Step-by-step explanation:
Answer:
6734 is the answer.
Step-by-step explanation:
834 x 3 = 2502.
1058 x 4 = 4232.
2502 + 4232 = 6734.
Determine whether each of the following functions is a solution of laplace's equation uxx + uyy = 0. (select all that apply. ).
Answers
Solution of laplace´s equation uxx + uyy = 0 including these function :
u(\(x^{2} + y^{2})\) = 0uxx = uyyu(xx) = u(yy)ux(x) = uy(y)u \((x+y)^{2}\) = 0Hence, the solutions of laplace´s equation is including the following functions above.
Read more about equation here :
https://brainly.com/question/25678139
Read more about function here :
https://brainly.com/question/25638609
#SPJ4
Find missing angles
X=???

Answers
help!!
use an inverse trig ratio to find the angle. round to the nearest degree.

Answers
The angles are approximately 16, 109, 81, and 45 degrees for 17, 73, 81, and 46 degrees, respectively.
How to use inverse trig ratio?To use an inverse trig ratio to find the angle, we need to be given a trigonometric function and its value. We can then use the inverse function to find the angle.
To find the angle whose tangent is 0.3, we use the inverse tangent function:
\($\tan^{-1}(0.3) \approx 16^{\circ}$\) (rounded to the nearest degree)
To find the angle whose cosine is -0.3, we use the inverse cosine function:
\($\cos^{-1}(-0.3) \approx 109^{\circ}$\) (rounded to the nearest degree)
Note that there are two possible angles whose cosine is -0.3 (one in the second quadrant and one in the third quadrant), but we choose the one in the second quadrant since it's between 0 and 180 degrees.
To find the angle whose sine is 0.98, we use the inverse sine function:
\($\sin^{-1}(0.98) \approx 81^{\circ}$\) (rounded to the nearest degree)
To find the angle whose tangent is 1, we use the inverse tangent function:
\($\tan^{-1}(1) = 45^{\circ}$\)
Therefore, the angles are approximately 16, 109, 81, and 45 degrees for 17, 73, 81, and 46 degrees, respectively.
To know more about Angle visit:
brainly.com/question/26167358
#SPJ1
14. Which value of c makes the inequality 4 + 3c > 10 true?
Answers
Answer:
C=6
Step-by-step explanation:
3x2 is 6 and 6+4= 10.
This question can be answered using trial and error.
Hi student, let me help you out!
............................................................................................................
Which value of c makes the inequality 4+3c>10 true? We can quickly find it if we follow these steps:
Subtract 4 from both sides.Solve for c.Step 1. Subtract 4 from both sides: \(\mathrm{3c > 10-4}\).
Upon simplifying, we get \(\mathrm{3c > 6}\).
Step 2. Solve for c by dividing both sides by 3: \(\mathrm{c > 2}\)
So the values that make this inequality true are greater than 2.
Hope it helped you out, ask in comments if any queries arise. :)
State if the two triangles are congruent. If they are, state how you know.

Answers
Explanation:
The angles marked with a single arc are one pair of congruent angles forming one "A" of "ASA".
The other "A" is the angles marked with double arcs.
The "S" refers to the sides between those said angles. These sides overlap perfectly so we have a shared side, meaning they must be the same length (refer to the reflexive property).
This is why the triangles are congruent by the ASA (angle side angle) congruence theorem. One triangle is a reflected version of the other. The mirror line being that shared overlapping side. Congruent triangles are like twin identical copies.
(5 points) how many revolutions will a car wheel of 30 in. (diameter) make as the car travels 1 mile?
Answers
We need to know about circumference of a circle to solve the problem. The number of revolutions that the car wheel makes to travel 1 mile is 672.
The circumference of the circle is the perimeter of the circle. In the given question we know that the diameter of the car wheel is 30 inches, and we need to find out the number of revolutions it will take for the car to travel 1 mile. We need to find the circumeference of the circle from there we will know how much distance it covers in one revolution, so we can find out after that the number of revolutions it will take to cover 1 mile.
radius= 30/2 = 15 inches
circumference= 2\(\pi\)r = 2x \(\pi\)x 15=94.25 sq inches
1 mile = 63360 inches
revolutions = 63360/94.25= 672
Therefore the number of revolutions the car will make to travel 1 mile is 672.
Learn more about circumference from here:
https://brainly.com/question/27447563
#SPJ4
Subtract the following polynomials.

Answers
The subtraction of the polynomials (3.1x + 2.8z) - (4.3x - 1.2z) is -1.2x + 4x
How to subtract polynomials?A polynomial is an expression consisting of a sum of a finite number of terms, each term being the product of a constant coefficient and one or more variables raised to a non-negative integer power.
(3.1x + 2.8z) - (4.3x - 1.2z)
open parenthesis
3.1x + 2.8z - 4.3x + 1.2z
combine like terms
3.1x - 4.3x + 2.8z + 1.2z
-1.2x + 4x
Ultimately, -1.2x + 4x is the results of the subtraction of the polynomial.
Read more on polynomials:
https://brainly.com/question/4142886
#SPJ1
solve the following system by elimination
4x-4y=-12
12z-6y=-6
Answers

Which of the following correlation coefficients represents the strongest relationship between two variables? -.75 +.60 .00 +.30
Answers
The correlation coefficient that represents the strongest relationship between two variables is -0.75.
In correlation coefficients, the absolute value indicates the strength of the relationship between variables. The strength of the association increases with the absolute value's proximity to 1.
The maximum absolute value in this instance is -0.75, which denotes a significant negative correlation. The relevance of the reverse correlation value of -0.75 is demonstrated by the noteworthy unfavorable correlation between the two variables.
To know more about correlation coefficients, visit,
https://brainly.com/question/4219149
#SPJ4
the difference of n and 15 is less than or equal to 37
Answers
Answer: n ≤ 52
Step-by-step explanation:
less than or equal to is usually write as ≤.
n - 15 ≤ 37
+15 +15 [Add 15 to the both sides]
n ≤ 52