Q9. Calculate the area of this rectangle in cm² 4.3 cm 2.5cm
Answers
Answer: 10.75
Step-by-step explanation: 1: Based on the given conditions, formulate: 4.3 x 2.5
2: Calculate 4.3 x 2.5 = 10.75.
Therefore, the answer is 10.75.
Related Questions
12 cm
5 cm
10 cm
6 cm
Answers
The area of the frame that's not covered by the picture will be 12cm²
How to illustrate the information?From the information, a picture measuring 10cm by 5cn is mounted on a rectangular frame that's 12cm by 6cm.
The area of the frame that's not covered by the picture will be:
= (12 × 6) - (5 × 10)
= 72- 50
= 12cm
The area of the frame that's not covered by the picture will be 12cm²
Learn more about area on:
brainly.com/question/25292087
#SPJ1
A picture measuring 10cm by 5cn is mounted on a rectangular frame that's 12cm by 6cm. What is the area of the frame that's not covered by the picture?
Discrete Math
Numerical values only
a.) Suppose thatRis the relation { (i,j,k)|i, j, and k are integers with 0 < i < j < k < 6}. How many ordered triples are there in relationR?
b.) Suppose thatRis the relation { (a, b, c, d)|a, b, c, and d are positive integers anda \times b \times c \times d= 6}. What is|R|?
c.) Suppose thatRis the relation { (a, b, c, d)|a, b, c, and d are positive integers anda \times b \times c \times d = 6}. Is(2,1,3,2)\in R? (Answer yes or no)
d.) Suppose thatRis the relation { (i, j, k)|i, j, and k are integers with 0 < i < j < k < 6 }. Is(1, 3, 4) \in R? (Answer yes or no)
Answers
a) the total number of ordered triples in relation R is: 5 * 4 * 3 = 60
b) the cardinality of relation R is |R| = 10.
c) Since the product is not equal to 6, (2, 1, 3, 2) is not in relation R. The answer is "no".
d) Since 1 < 3 < 4 and all elements are integers between 0 and 6, (1, 3, 4) satisfies the conditions and is in relation R. The answer is "yes".
What is cardinality?
In mathematics, cardinality is a concept that refers to the "size" or "number of elements" in a set. It is a measure of the quantity of elements present in a set, disregarding any specific order or arrangement.
a) To count the number of ordered triples in relation R, we need to consider the given conditions: 0 < i < j < k < 6.
Since i, j, and k are integers, we have 5 choices for k (1, 2, 3, 4, or 5). For each choice of k, we have (k-1) choices for j (as j must be smaller than k). Finally, for each choice of j, we have (j-1) choices for i.
Therefore, the total number of ordered triples in relation R is:
5 * 4 * 3 = 60
b) To find the cardinality of relation R, we need to count the number of ordered quadruples (a, b, c, d) that satisfy the condition a * b * c * d = 6.
The prime factorization of 6 is 2 * 3, and since a, b, c, and d are positive integers, we have the following possibilities:
(2, 1, 1, 3), (2, 1, 3, 1), (2, 3, 1, 1)
(1, 2, 1, 3), (1, 2, 3, 1), (1, 3, 1, 2), (1, 3, 2, 1)
(3, 1, 1, 2), (3, 1, 2, 1), (3, 2, 1, 1)
Therefore, the cardinality of relation R is |R| = 10.
c) To determine if (2, 1, 3, 2) is in relation R, we need to check if the product of the four elements equals 6:
2 * 1 * 3 * 2 = 12
Since the product is not equal to 6, (2, 1, 3, 2) is not in relation R. The answer is "no".
d) To determine if (1, 3, 4) is in relation R, we need to check if the three elements satisfy the condition 0 < i < j < k < 6:
Since 1 < 3 < 4 and all elements are integers between 0 and 6, (1, 3, 4) satisfies the conditions and is in relation R. The answer is "yes".
To learn more about cardinality visit:
https://brainly.com/question/23976339
#SPJ4
1. A population of insects is very dynamic, depending on many variables. A simple model for a particular species of insect is found to be as given. 3- 12 +16 PO) 15 - 2+1 What happens to this population in the long run, i.e. will it die out (extinction), boom (grow indefinitely), or settle into an equilibrium (stability)? Justify your claim with the appropriate mathematics. If the result is equilibrium, then give the value of the stable population.
Answers
Therefore, the insect population will remain stable, neither increasing nor decreasing and the estimated stable population is 2.
Given the equation:3-12+16 PO) 15-2+1
In order to determine the stability of a population of insects, we must first calculate the equilibrium value of PO.
A population's equilibrium is defined as the point at which the population remains stable over time, indicating that the population is neither declining nor growing indefinitely.
Stable population equilibrium is defined as follows:
Let P* be the equilibrium value of the population.
This implies that:P* = 15 - 2 + 1 / 3 - 12 + 16
This simplifies to:P* = 14/7 or 2
Therefore, the equilibrium value of the insect population is 2. If the population is greater than 2, it will decrease. If it is less than 2, it will increase.
In this case, the population of insects will settle into an equilibrium state.
The value of the stable population is 2.
Know more about the equilibrium
https://brainly.com/question/24735820
#SPJ11
What are the four conditions necessary for X to have a Binomial Distribution? Mark all that apply.
a. There are n set trials.
b. The trials must be independent.
c. Continue sampling until you get a success.
d. There can only be two outcomes, a success and a failure
e. You must have at least 10 successes and 10 failures
f. The population must be at least 10x larger than the sample. T
g. he probability of success, p, is constant from trial to trial
Answers
Options a, b, d, and g are the correct conditions for a Binomial Distribution.
The four conditions necessary for X to have a Binomial Distribution are:
a. There are n set trials: In a binomial distribution, the number of trials, denoted as "n," must be predetermined and fixed. Each trial is independent and represents a discrete event.
b. The trials must be independent: The outcomes of each trial must be independent of each other. This means that the outcome of one trial does not influence or affect the outcome of any other trial. The independence assumption ensures that the probability of success remains constant across all trials.
d. There can only be two outcomes, a success and a failure: In a binomial distribution, each trial can have only two possible outcomes. These outcomes are typically labeled as "success" and "failure," although they can represent any two mutually exclusive events. The probability of success is denoted as "p," and the probability of failure is denoted as "q," where q = 1 - p.
g. The probability of success, p, is constant from trial to trial: In a binomial distribution, the probability of success (p) remains constant throughout all trials. This means that the likelihood of the desired outcome occurring remains the same for each trial. The constant probability ensures consistency in the distribution.
The remaining options, c, e, and f, are not conditions necessary for a binomial distribution. Option c, "Continue sampling until you get a success," suggests a different type of distribution where the number of trials is not predetermined. Options e and f, "You must have at least 10 successes and 10 failures" and "The population must be at least 10x larger than the sample," are not specific conditions for a binomial distribution. The number of successes or failures and the size of the population relative to the sample size are not inherent requirements for a binomial distribution.
Learn more about Binomial Distribution at: brainly.com/question/29137961
#SPJ11
what is 28.5 inches in height?
Answers
QUICK whoever gives correct answer will get brainliest please and thank you.

Answers
Hi! Im pretty sure its B, i took that test before and i think B is the correct answer!
Hope this helped you xx <3
Which points can be connected to draw a line of symmetry through this figure?
Responses
points A and C
points, A, and , F
points, E, and , F
points E and C

Answers
The points that can be connected to draw a line of symmetry through the figure shown are: C. points, E, and , F.
What is a Line of Symmetry?A line of symmetry, can be described as any line that divides a figure into two parts, in such a way that the divided parts are identical to each other, which implies that they can be folded onto each other.
A line of symmetry is also called a mirror line or axis of symmetry of a shape. The line simply creates mirror images that are identical to each other when the figure is cut across.
The figure given is a rectangle having the indicated points. If we connect point E to point F, the figure will be divided into equal halves. Therefore, the answer is: C. points, E, and , F
Learn more about Line of Symmetry on:
https://brainly.com/question/29449904
#SPJ1
0(-7) helppppppppppppppppppppp
Answers
Answer:
0
Step-by-step explanation:
anything multuplied by 0 is 0
Lame Example Furniture Company makes two products for its adoring public: chairs (C)and tables (T). Each chair requires 5 hours of labor (L) and 4 linear feet of rich mahogany (M), and each table requires 3 hours of labor and 20 linear feet of rich mahogany. The company has 240 labor hours available this week, and the warehouse has 700 linear feet of rich mahogany available. Profit for each chair is $150 and for each table is $750. At the optimal solution, how many tables should be produced? What is the maximum profit?
Answers
Maximize: Profit = 150C + 750T
Subject to:
5C + 3T ≤ 240 (Labor constraint)
4C + 20T ≤ 700 (Material constraint)
C ≥ 0
T ≥ 0
To determine the optimal production quantity of tables and the maximum profit, we can set up a linear programming problem based on the given information.
Let's define the decision variables:
Let C represent the number of chairs produced.
Let T represent the number of tables produced.
Objective function:
The objective is to maximize profit. The profit for each chair is $150, and the profit for each table is $750. Therefore, the objective function can be expressed as:
Profit = 150C + 750T
Constraints:
Labor constraint: The total labor hours available is 240, and each chair requires 5 hours, while each table requires 3 hours. So the labor constraint can be represented as:
5C + 3T ≤ 240
Material constraint: The warehouse has 700 linear feet of rich mahogany available, and each chair requires 4 linear feet, while each table requires 20 linear feet. Therefore, the material constraint can be expressed as:
4C + 20T ≤ 700
Non-negativity constraint: Since we cannot produce a negative quantity of chairs or tables, both C and T should be greater than or equal to zero:
C ≥ 0
T ≥ 0
Now, we can solve the linear programming problem to find the optimal solution:
Maximize: Profit = 150C + 750T
Subject to:
5C + 3T ≤ 240 (Labor constraint)
4C + 20T ≤ 700 (Material constraint)
C ≥ 0
T ≥ 0
Learn more about profit from
brainly.com/question/29087694
#SPJ11
how do I solve this?

Answers
Answer:
We conclude that the range of the function will be:
R = {5, 17, 29}
Step-by-step explanation:
Given
Given the function
f(x) = 6x-1
Given the domain
D = {0, 3, 5}
To Determine:
The range R = ?
We know that range of the function consists of all the y-values for the x-values in the domain of the function.
so substituting the values of x = 0, 3, and 5 in the function to determine the corresponding y-values.
Plug in x = 0
y = 6x-1
y = 6(0) - 1 = 6-1 = 5
Plug in x = 3
y = 6x-1
y = 6(3) - 1 = 18-1 = 17
Plug in x = 5
y = 6x-1
y = 6(5) - 1 = 30-1 = 29
Now, combine all the determined y-values which are 5, 17, and 29.
Therefore, we conclude that the range of the function will be:
R = {5, 17, 29}
If tanθ = 13 what is the value of 7sin2θ+3cos2θ
Answers
I think the question should be tan theta = 1/√3, but I have given the solutions of both.
Hope it helps.
If you have any query, feel free to ask.

a 10-unit vector at 60° from the vertical has a vertical component with a magnitude
Answers
Answer:
i hop this halp
Step-by-step explanation:
less than 10 units.
ethan bought 4 packages of pencils. after he gave 8 pencils to his friends, he had 40 pencils left over. how many pencils were in each package? use the drop-down menus to solve the problem arithmetically and algebraically
Answers
Answer:
there was 12 pencil's in each package because 12 ×4=48 48 -8=40
Work out(−3)2−3×(2×54)÷112
Answers
Answer:
-249/28
Step-by-step explanation:
Identify which equation represents a line parallel to the given equation 2x+5=25 asap please
Answers
Answer:
10
Step-by-step explanation:
2x(+5)=(25)< subtract 5 to each side
2x=20<divide 2 to 20
x=10
²\(2x^2-1414x=24\)
Answers
The results of a series of surveys revealed a population with a mean of 4.73 and a standard deviation of 0.865. If each survey has a sample size of 200, which value falls within the interval where 95% of the sample means occur? A. 4.88 B. 4.63 C. 4.91 D. 4.55
Answers
Answer:
4.63
Please give me brainliest, I really need it.

The value of 4.63 falls within the interval (4.66, 4.791) where 95% of the sample means occur option (B) is correct.
What is a confidence interval for population standard deviation?It is defined as the sampling distribution following an approximately normal distribution for known standard deviation.
The formula for finding the confidence interval for population standard deviation as follows:
\(\rm s\sqrt{\dfrac{n-1}{\chi^2_{\alpha/2, \ n-1}}} < \sigma < s\sqrt{\dfrac{n-1}{\chi^2_{1-\alpha/2, \ n-1}}}\)
Where s is the standard deviation.
n is the sample size.
\(\chi^2_{\alpha/2, \ n-1} and \chi^2_{1-\alpha/2, \ n-1}\) are the constant based on the Chi-Square distribution table.
α is the significance level.
σ is the confidence interval for population standard deviation.
Calculating the confidence interval for population standard deviation:
We know significance level = 1 - confidence level
It is given that:
Mean of the population x = 4.73
Standard deviation s = 0.865
Sample size n = 200
The interval where 95% of the sample means occur:
Lower limit = 4.73 - 0.865/√200
Lower limit = 4.66
Upper limit = 4.73 + 0.865/√200
Upper limit = 4.791
The interval = (4.66, 4.791)
Thus, the value of 4.63 falls within the interval (4.66, 4.791) where 95% of the sample means occur option (B) is correct.
Learn more about the confidence interval here:
brainly.com/question/6654139
#SPJ2
Which expression is equivalent to 10f - 5f + 8 +6g +4
Answers
Answer:5f+6g+12
Step-by-step explanation:
Just did it and got it right
The value of equivalent expression is,
⇒ 5f + 6g + 12
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
We have to given that;
The expression is,
⇒ 10f - 5f + 8 + 6g + 4
Now, We can simplify as,
⇒ 10f - 5f + 8 + 6g + 4
Combine like terms,
⇒ 5f + 6g + 12
Thus, The equivalent expression is,
⇒ 5f + 6g + 12
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ5
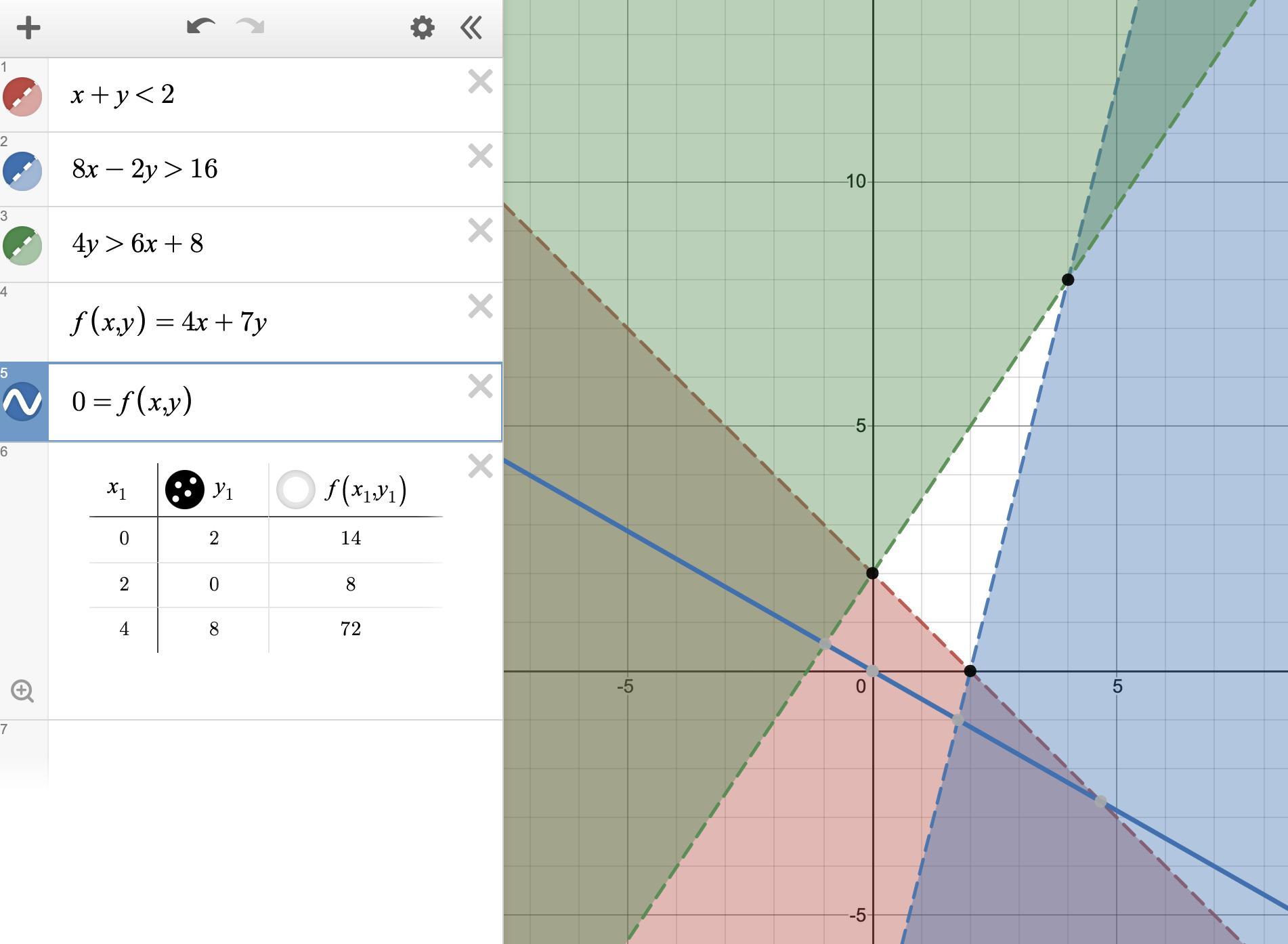
Find the maximum and minimum values of the function for the polygonal convex set determined by the given system of
inequalities.
x+y>2
8x-2y< 16
4y <6x+8
f (x, y) = 4x+7y

Answers
Answer:
max: 72 at (4, 8)
min: 8 at (2, 0)
Step-by-step explanation:
The attached graph shows the solution set as a white area. The shaded areas are excluded from the solution set. The dashed boundary lines indicate those lines are not excluded from the set. The vertices of the polygon are (0, 2), (2, 0) and (4, 8).
The line f(x,y) = 0 is shown for reference. The maximum value of f(x,y) will be found at the vertex of the solution set that is farthest from this line. The minimum will be found at the vertex of the solution set that is closest to this line.
The maximum value of f(x, y) is 72 at (x, y) = (4, 8).
The minimum value of f(x, y) is 8 at (x, y) = (2, 0).
Find an equation of the sphere with center (-3, 2, 6) and radius 5. What is the intersection of this sphere with the yz-plane? x = 0
Answers
The intersection of the sphere with the yz-plane is a circle centered at (2, 6) with a radius of 5.
The equation of a sphere with center (h, k, l) and radius r is given by (x - h)^2 + (y - k)^2 + (z - l)^2 = r^2. In this case, the center is (-3, 2, 6) and the radius is 5, so the equation of the sphere is (x + 3)^2 + (y - 2)^2 + (z - 6)^2 = 25.
To find the intersection of the sphere with the yz-plane (x = 0), we substitute x = 0 into the equation of the sphere. This gives (0 + 3)^2 + (y - 2)^2 + (z - 6)^2 = 25, which simplifies to 6^2 + (y - 2)^2 + (z - 6)^2 = 25. This equation represents a circle in the yz-plane centered at (2, 6) with a radius of 5.
Therefore, the intersection of the sphere with the yz-plane is a circle centered at (2, 6) with a radius of 5.
Know more about Equation here:
https://brainly.com/question/29538993
#SPJ11
DUE TODAY! WILL
MARK BRAINLIEST
4. Find the measure of arc RT. Fill in the blank with the number only.
Assume that segments that appear to be tangent are tangent.

Answers
Answer:
he number only.
Assume that segments that appear to be tangent are tangent.
Step-by-step explanation:
In Exercises 9 and 10, find the value of x so that f(x) = 7.

Answers
Answer:
the answer is 15 i took the test
Step-by-step explanation:
In exercise 9, the function f(x) is equal to 7 when x is equal to 3.
In exercise 10, the function f(x) is equal to 7 when x is equal to 4.
How do we do the calculation?exercise 9:
f(x) = 7
f(3) = 7
x = 3
We conclude that the function f(x) is equal to 7 when x is equal to 3 and can be seen from the graph of the function, which shows that the function passes through the point (3, 7).
Exercise 10:
f(x) = 7
f(4) = 7
x = 4
We conclude that the function f(x) is equal to 7 when x is equal to 4 and can be seen from the graph of the function, which shows that the function passes through the point (4, 7).
Learn more about graph at:
https://brainly.com/question/19040584
#SPJ2
evaluate the integral by reversing the order of integration. 3 0 9 5ex2 dx dy 3y
Answers
To evaluate the given integral by reversing the order of integration, we first need to write it in terms of the new order. This can be done by considering the limits of integration for each variable. The original integral is:∫[0 to 3]∫[0 to 9] 5e^(2x) dx dyTo reverse the order of integration, we need to first consider the limits of integration for y. The limits for y are from 0 to 3, which means that the integral with respect to y will have these limits.
To evaluate the integral by reversing the order of integration. The given integral is:
∫(from 0 to 3) ∫(from 5 to 9) 5e^(x^2) dx dy.
To reverse the order of integration, we first need to find the new limits of integration. Currently, the region is defined by:
0 ≤ y ≤ 3
5 ≤ x ≤ 9
We will switch the order of integration to dy dx. To do this, we express y in terms of x:
x = 5
x = 9
So the new region is defined by:
5 ≤ x ≤ 9
0 ≤ y ≤ 3
Now, we rewrite the integral with the new order of integration:
∫(from 5 to 9) ∫(from 0 to 3) 5e^(x^2) dy dx.
Now, let's evaluate the integral step by step:
Step 1: Evaluate the inner integral with respect to y.
∫(0 to 3) 5e^(x^2) dy = 5e^(x^2) * y | evaluated from y=0 to y=3
= 15e^(x^2)
Step 2: Evaluate the outer integral with respect to x.
∫(5 to 9) 15e^(x^2) dx
Unfortunately, this integral does not have a closed-form . To obtain a numerical result, you would need to use numerical integration methods, such as Simpson's rule or the trapezoidal rule.
To learn more about integration : brainly.com/question/18125359
#SPJ11
Lee wanted to visit his grandmother who lives 1,400 air miles
away. If Lee's plane travels 400 miles per hour, how many
hours would Lee's flight take?
Answers
Answer:
Lee's flight would take 3.5 hours.
Step-by-step explanation:
1400 ÷ 400 = 3.5
Determine the following limits. Enter DNE if a limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter or -00, as appropriate. • lim 63 + 36.x" + 9x – 5 = lim 1 - 00 6x + 36x² + 9.c – 5
Answers
The limit is equal to -5/9 as x approaches negative infinity.
To evaluate the limit, we can divide the numerator and denominator by the highest power of x, which is x^2. This gives:
lim (63/x^2 + 36/x + 9 - 5/x^2) / (6/x^2 + 36 + 9/x - 5/x^2)
As x approaches negative infinity, all the terms in the numerator and denominator tend to zero except for the constant terms. Therefore, the limit is equal to:
lim (-5/x^2) / (-5/x^2) = 1
Multiplying by the constant -5/9, we get:
lim (-5/9) * (1) = -5/9
Therefore, the limit is -5/9 as x approaches negative infinity.
Learn more about infinity here
https://brainly.com/question/7697090
#SPJ11
Nora was offered a job that paid a salary of $40,000 in its first year. The salary was set to increase by 3% per year every year. If Nora worked at the job for 21 years, what was the total amount of money earned over the 21 years, to the nearest whole number?
Answers
The total amount of money earned by Nora salary over the 21 years is approximately $1,848,000.
To find the total amount of money earned by Nora over 21 years, we need to calculate the salary for each year and then sum them up.
In the first year, Nora's salary is $40,000.
In the second year, her salary will be increased by 3%, so it will be:
$40,000 + 3% of $40,000 = $40,000 + $1,200 = $41,200.
In the third year, her salary will again increase by 3%, so it will be:
$41,200 + 3% of $41,200 = $41,200 + $1,236 = $42,436.
We can continue this process for each year, adding 3% of the previous year's salary to calculate the next year's salary.
To calculate the total amount of money earned over the 21 years, we need to sum up the salaries for each year. Here's the calculation:
Total = $40,000 + $41,200 + $42,436 + ... (21 terms)
To simplify the calculation, we can use the formula for the sum of an arithmetic series:
Total = (n/2) * (2a + (n - 1)d)
where:
n = number of terms (21 in this case)
a = first term ($40,000)
d = common difference (3% of the previous year's salary)
Plugging in the values:
Total = (21/2) * [2(40,000) + (21 - 1)(0.03)(40,000)]
Simplifying further:
Total = (21/2) * [80,000 + 20(0.03)(40,000)]
= (21/2) * [80,000 + 2,400(40,000)]
= (21/2) * [80,000 + 96,000]
= (21/2) * 176,000
= 21 * 88,000
= 1,848,000
Therefore, the total amount of money earned by Nora salary over the 21 years is approximately $1,848,000.
For such more questions on Total earnings by Nora
https://brainly.com/question/27106278
#SPJ11
I NEED HELP W THIS QUESTION PLS BE FASTT

Answers
The area of the figure composed of the square and four semicircles is approximately 242.4 square units.
Describe Semicircle?A semicircle is a two-dimensional geometric shape that is half of a circle. It is formed by drawing a diameter of a circle and then drawing the arc that connects the two endpoints of the diameter. The diameter divides the circle into two equal parts, each of which is a semicircle.
A semicircle has several important properties, including:
It has one straight side, which is the diameter of the circle.
The other side is curved, and it is a half-circle.
The radius of the semicircle is equal to half the diameter of the circle.
The circumference of a semicircle is half the circumference of the circle.
The area of a semicircle is half the area of the circle.
Semicircles are used in many applications of geometry and trigonometry, including in the study of angles, arcs, and circles. They are also used in architecture and engineering to design buildings, bridges, and other structures that have semicircular features.
In addition to being a geometric shape, a semicircle can also refer to a half-circle that is used as a decorative element or design motif. Semicircles are often used in art, architecture, and graphic design to create visually interesting patterns and compositions.
To find the area of the figure composed of a square and four semicircles, we need to first find the area of the square and the area of the four semicircles. Then, we can subtract the area of the four semicircles from the area of the square to get the total area of the figure.
The area of the square is simply the side length squared, so in this case it is:
Area of square = (22)^2 = 484 square units
The diameter of each semicircle is equal to the side length of the square, so the radius is half of that or 11 units. Therefore, the area of each semicircle is:
Area of semicircle = (1/2) * π * r^2 = (1/2) * π * 11^2 = 60.4 square units
Since there are four semicircles, the total area of the four semicircles is:
Total area of semicircles = 4 * Area of semicircle = 4 * 60.4 = 241.6 square units
To get the area of the entire figure, we need to subtract the area of the four semicircles from the area of the square:
Area of figure = Area of square - Total area of semicircles
Area of figure = 484 - 241.6 = 242.4 square units
Rounding this to the nearest tenth gives:
Area of figure = 242.4 (rounded to the nearest tenth)
Therefore, the area of the figure composed of the square and four semicircles is approximately 242.4 square units.
To know more about area visit:
https://brainly.com/question/12187609
#SPJ1
independent or dependent?!! (look at attachment)

Answers
Answer:
independent
Step-by-step explanation:
The length of a triangle is 2x cm, 3x cm, and 4x cm. The perimeter of the triangle is 81 cm. Calculate the value of x.
Answers
Answer: 9
Step-by-step explanation:
To find the perimeter of the Triangle, add all 3 sides together
So 2x + 3x + 4x = 81
9x = 81
Divide both sides by 9
x=9
My geometry teacher sucks i have no clue how to do all four of these

Answers
The value of x is 10.
What is the Pythagoras theorem?The Pythagoras theorem states that the square of the longest side must be equal to the sum of the square of the other two sides in a right-angle triangle.
|AC|^2 = |AB|^2 + |BC|^2
Given;
Base=6
Perpendicular=8
Now
x^2=6^2+8^2
X^2=36+64
X^2=100
x=10
Therefore, by pythagoras theorem the answer will be 10.
Learn more about Pythagoras theorem;
https://brainly.com/question/343682
#SPJ1