Question 140. In the equation 2x^2 - 3x + 4 = 0, what is the sum of the squares of the roots?

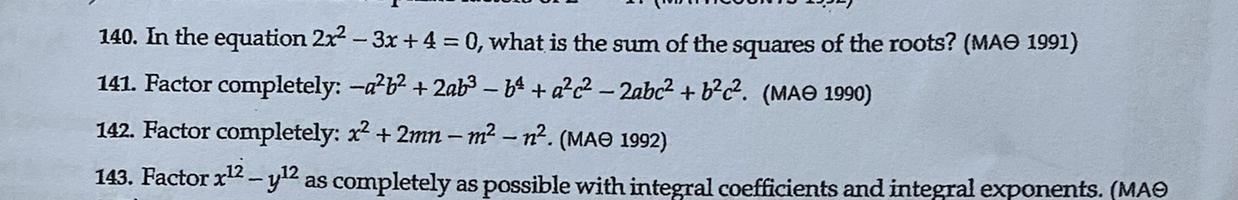
Answer:16x16

Step-by-step explanation:

Answer: 2a < 2b

Step-by-step explanation:

We are given a statement:

a < b and b < c, then 2a ____ 2b

We can use simple numbers that make the statement true.

Where,

a = 2

b = 3

c = 4

Now lets plug it in.

2 < 3 and 3 < 4, then 2(2) ____ 2(3)

and lets simplify:

2 < 3 and 3 < 4, then 4 ____ 6

We can see that 4 is less than 6,

so as a is less than b, 2a is less than 2b.

The only thing changing is the coefficient being multiplied by the variables a and b.

v + 29 = 73

v = 73 - 29

v = 46

Step-by-step explanation:

first you put the equation and then you solve it by the way I did

The number which is written on the board according to the description in the task content is; 12.

It follows from the task content that the number which is written on the board is to be determined.

Let the number in discuss which is written on the board be represented by x;

Therefore, since one student increased the number by 12; we have; x + 12.

Also, another student multiplied the number by 3; we have; 3x.

Ultimately, since the first student's results is 2 greater than the second student result, we have;

x + 12 = 3x + 2.

-2x = -10

Divide both sides by -2;

x = 5

Ultimately, the number which is written on the board according to the description in the task content is; 5.

Read more on word problems;

https://brainly.com/question/13818690

#SPJ1

The equation given in the task content; -3 ( x-3) -1 = ax + b will have infinite amount of solutions if; a = -3 and b = 8.

It follows from the task content the condition form which the equation given would have infinite amount of solutions be determined.

Recall that a linear equation; mx + p = nx + r is said to have infinite amount of solutions if; m = n and p = r.

Therefore, by evaluation of the given equation; -3( x-3) -1 = ax + b; we have;

-3x + 9 - 1 = ax + b

-3x + 8 = ax + b

Consequently, the equation is said to have infinitely many solutions if; a = -3 and b = 8.

Read more on infinitely many solutions;

https://brainly.com/question/21231737

#SPJ1

The relationship between linear speed and angular speed is given by:

so:

therefore:

Step-by-step explanation:

Simple, she found the sum of the interior angles not exterior angles.

The exterior angles of any polygon add up to 360 degrees.

What Cindy did was found the total interior angle measure of a hexagon which is 720

n = 5 is the smallest number such that both expressions are rational numbers.

Here we have two expressions that depend on the value of n.

√(76 + n)

√(2n + 26)

We will get rational numbers only if the arguments are perfect squares.

Now, two perfect squares are 81 = 9*9 and 36 = 6*6

So, if we take n = 5 we will get:

76 + 5 = 81

2*5 + 26 = 10 + 26 = 36

So with n = 5 we get two perfect squares, and that is the smallest value that n can take (just by trial and error).

Learn more about rational numbers:

https://brainly.com/question/12088221

#SPJ1

\( {\qquad\qquad\huge\underline{{\sf Answer}}} \)

Here we go ~

\(\qquad \sf  \dashrightarrow \: 1 \: \: cm {}^{3} = \cfrac{1}{1000000} \: \: m {}^{3} \)

\(\qquad \sf  \dashrightarrow \: 1 \: \: cm {}^{3} = \cfrac{1}{10 {}^{6} } \: \: m {}^{3} \)

\(\qquad \sf  \dashrightarrow \: 1 \: \: cm {}^{3} = {}{10 {}^{ - 6} } \: \: m {}^{3} \)

Answer:

200 lbs.

Step-by-step explanation:

Divide mass value by 16 to convert oz to lbs.

3,200/16=200

Answer:

it's 3 in 3x and 6 in 6y I think but im not sure i haven't done this in a while

The graph of the function y = -3√x - 6 is a downward translation of 6 units with a vertical reflection compared to the graph of the parent function y = √x.

To graph the transformed function y = -3√x - 6, we will apply the following transformations to the parent function y = √x:

Translation:

Reflection:

The graph is reflected over the x-axis due to the negative coefficient (-3) in front of the square root function. This means that each point on the transformed graph is vertically flipped in relation to the corresponding point on the parent graph.

Read more about graph

brainly.com/question/16418380

#SPJ1

The slope of the curve  y⁴ = y² - x² is 1 and repeat the process for the second point.

Find the slopes of the curve y⁴ = y² - x² at the given points, we need to differentiate the equation implicitly with respect to x.
Differentiating both sides of the equation with respect to x, we get:
4y³ * (dy/dx) = 2y * (dy/dx) - 2x
Next, we can solve for (dy/dx) by isolating it on one side of the equation:
4y³ * (dy/dx) - 2y * (dy/dx) = -2x
(2y - 4y³) * (dy/dx) = -2x
(dy/dx) = -2x / (2y - 4y³)
Now, substitute the x and y values for each point into the equation to find the slopes at those points.
For example, if one point is (1, 1), we substitute x = 1 and y = 1 into the equation:
(dy/dx) = -2(1) / (2(1) - 4(1)³)
(dy/dx) = -2 / (2 - 4)
(dy/dx) = -2 / -2
(dy/dx) = 1
Repeat the process for the second point, and you will have the slopes of the curve at both points.

For more such questions on slope  visit:

https://brainly.com/question/16949303

#SPJ8

Answer:

isosceles triangle

Step-by-step explanation:

first by using corresponding angle theorem:

<A=<C

<A=50°

then by using exterior angle theorem:

<A+<C=<B(the outer angle)

50°+<C=<B,<B=180°-80°(angle B lies in a staight line)

<B=100°

50°+<C=100°

<C=50°

Answer:

~

Step-by-step explanation:

To make it easier to graph using a translation, we can rewrite the given equation as:

y - 5 = √√4x + 16

This is obtained by subtracting 5 from both sides of the equation.

The graph of the original equation y = √√4x+16 +5 can be obtained by taking the graph of y = √√4x + 16 and shifting it upwards by 5 units. The graph of y = √√4x + 16 is a square root function that has a vertical stretch of 2, a horizontal compression of 4, and a vertical translation of 16 units upwards. So the graph of the given equation y = √√4x+16 +5 will be the same as the graph of y = √√4x + 16, but shifted upwards by 5 units.

Answer:

9

Step-by-step explanation:

divide 27 by 3

It equals 9

9 x 2 = 18 boys

27-18= 9 girls

Answer:

Step-by-step explanation:

D∩L={f}

D∪L={a,f,g,j,k}

Answer:

c= -17

Step-by-step explanation:

2=10c-8c+36

2=2c+36

-34=2c

c= -17

Check:

2=10(-17)-4[2(-17)-9]

2= -170-4(-34-9)

2= -170+136+36

2=2

Answer:

23 ft

Step-by-step explanation:

The computation of the maximum length of the base of the triangle is as follows:

Area of triangle is = 4 × 6 ÷ 2

= 12 ft²

Now the maximum area of the rectangle is

= 150 - 12

= 138 ft²

L = ?

W = 6 ft

Area of rectangle is  = L × W

L × 6 = 138

L = 138 ÷ 6

= 23 ft

Answer:

radius = 6

apothem = 4.85

side length = 7.05

Step-by-step explanation:

sin 36 =x/6, x= 3.53, side length = 7.05

cos 36 = apothem/6, apothem = 4.85

Therefore, the values of the pentagon is the radius is 6, apothem=4.8 and the side length =3.48.

A pentagon is one of the many types of polygon having five sides and five angles. The word 'Pentagon' arises from two words, that are, ‘Penta’ and ‘Gonia,’ meaning five angles.

Let x be the side length of the pentagon.

As per the given information;

Apothem is the line from the center of the pentagon to a side, intersecting the side at 90 degrees right angle.

Sin(36) = x / 6

x = 6 × sin(36)

side length x = 6 × (0.58)

side length x  = 3.48

And

cos(36) = apothem / 6

Apothem = 6 cos36

Apothem = 6 (0.80)

Apothem = 4.8

Hence, the radius is 6, apothem=4.8 and the side length x=3.48.

To know more about the pentagon;

https://brainly.com/question/26170435

#SPJ6

Based on the fact that the sum of the interior angles need to be equal to 180°, the missing angle is 110°

The sum of all the interior angles need to add up to 180° which means that to find the missing angle, you should subtract the known angles from 180°.

The missing angle is:

= Total angle - Known angles

Solving for the missing angle gives:

= 180 - 21 - 49

= 180 - 70

= 110°

Find out more questions on missing angles at https://brainly.com/question/23991796

#SPJ1

Answer:

Step-by-step explanation:

Answer:  6 * 24 = 144 ways.

Step-by-step explanation:

Solution:

Given word => DANGER.

The condition is that vowels can't occupy odd places so, we will let them occupy even places.

A total number of arrangements will be = 6 * 24 = 144 ways.

Answer: 6x24 = 144 ways.

Using the coordinate geometry formula, the exact area of triangle DEF is: B. 18 square units.

The coordinate geometry formula is used to find the rea of a triangle with given coordinates of its vertices. It is given as: the absolute value of [Dx(Ey - Fy) + Ex(Fy - Dy) + Fx(Dy - Ey)]/2.

Dx = -3

Dy = 4

Ex = 3

Ey =-2

Fx = 3

Fy = 4

Plug in the values:

[-3(-2 - 4) + 3(4 - 4) + 3(4 - (-2))]/2.

[-3(-6) + 3(0) + 3(6)]/2.

[18 + 0 + 18]/2.

36/2

= 18 units²

Learn more about the coordinate geometry formula on:

https://brainly.com/question/15383389

#SPJ1

Answer:c

Step-by-step explanation:

Did the test

Answer:

D. 2:1 & 6:3

Step-by-step explanation:

Proportion means equal so we need to see which ratios are equal.

To do that we need to make one fo the numbers in the ratio equal the corresponding number in the other ratio, then see if the other matches.

A:

1:2 & 4:2

The second number is already the same but the first isn't, therefore it is not proportional.

B:

1:2 & 6:3

To get 1 to equal 6 we must multiply it by 6, and what you do to one side you must do to the other so we have to multiply 2 by 6 as well

6:12 & 6:3

The first numbers are the same but the second isn't, therefore it is not proportional.

C:

2:1 & 2:4

The first numbers are the same but the second isn't, therefore it is not proportional

D:

2:1 & 6:3

to get 2 to equal 6 we need to multiply it by 3, which means we have to multiu 1 by 3 too

6:3 & 6:3

These are equal so this is proportional.

Answer:

{x,y} = {19/12,5/6}

Step-by-step explanation:

20√3 in² is the required area of the trapezoid in simplest form

The formula for calculating the area of a trapezoid is expressed as:

A = 1/2(a+b)*h

where

a and b are the sides

h is the height of the trapezoid

Given the following

a = 14in

b =26 in

For the height:

tan 60 = h/6

h = 6tan60

h = √3

Substitute

A = 1/2(14 + 26)*√3

A = 20√3 in²

Hence the  area of the trapezoid in its simplest radical form is 20√3 in²

Learn more on area of the trapezoid here: https://brainly.com/question/1410008

#SPJ1

I. The solution to the system of equations using Gaussian elimination is x = 1, y = -1, and z = 2.

II. For the LU-decomposition method, we need to have a square coefficient matrix, which is not the case in the given system. Therefore, we cannot directly apply the LU-decomposition method.

III. For this method to converge, the coefficient matrix must be diagonally dominant, which is not the case in the given system. Therefore, the Gauss-Jacobi method cannot be directly applied either.

IV. It requires the coefficient matrix to be diagonally dominant, which is not satisfied in the given system. Hence, the Gauss-Seidel method cannot be directly used.

I. Gaussian Elimination Method:

To solve the system of linear equations using Gaussian elimination, we perform row operations to reduce the system into upper triangular form. The augmented matrix for the given system is:

| 6 2 -1 | 4 |

| 1 5 1 | 3 |

| 2 1 4 |27 |

We can start by eliminating the coefficients below the first element in the first column. To do this, we multiply the first row by a suitable factor and subtract it from the second and third rows to eliminate the x coefficient below the first row. Then, we proceed to eliminate the x coefficient below the second row, and so on.

After performing the necessary row operations, we obtain the following reduced row-echelon form:

| 6 2 -1 | 4 |

| 0 4 2 | -1 |

| 0 0 3 | 6 |

From this form, we can easily back-substitute to find the values of x, y, and z. We have z = 2, y = -1, and x = 1.

II. LU-Decomposition Method:

LU-decomposition is a method that decomposes a square matrix into a product of two matrices, L and U, where L is lower triangular and U is upper triangular.

III. Gauss-Jacobi Method:

The Gauss-Jacobi method is an iterative numerical method to solve systems of linear equations.

IV. Gauss-Seidel Method:

Similar to the Gauss-Jacobi method, the Gauss-Seidel method is an iterative method for solving linear systems.

Therefore, out of the four methods mentioned, only the Gaussian elimination method can be used to solve the given system of linear equations.

For more such questions on solution

https://brainly.com/question/24644930

#SPJ8

Answer:

first term (a)=-2

common difference (d)=8

Now,

87th term=a+(n-1)d

=-2+(87-1)×8

=-2+86×8

=-2+688

=686

Since we are only interested in the positive solution, the time it will take for her to land safely on the net is:

t = 1 second.

To write a quadratic function to represent the height h of the acrobat t seconds after the jump, we can use the following formula:

\(h(t) = -16t^2 + vt + h0\)

Where h0 is the initial height of the acrobat, which is 25 feet, and v is the initial vertical velocity, which is 4 ft/s. Plugging in these values, we get:

\(h(t) = -16t^2 + 4t + 25\)

To find how long it will take for her to land safely on the net, we need to find the time at which h(t) = 5. In other words, we need to solve the equation:

\(-16t^2 + 4t + 25 = 5\)

Simplifying this equation, we get:

\(-16t^2 + 4t + 20 = 0\)

Dividing both sides by -4, we get:

\(4t^2 - t - 5 = 0\)

Now we can use the quadratic formula to solve for t:

\(t = (-b ± \sqrt(b^2 - 4ac)) / 2a\)

Where a = 4, b = -1, and c = -5. Plugging in these values, we get:

\(t = (1 ± \sqrt(1 + 4(4)(5))) / 8\)

Simplifying this equation, we get:

\(t = (1 ± 9) / 8\)

So, the two solutions are:

\(t = 1 and t = -5/4\)

Since we are only interested in the positive solution, the time it will take for her to land safely on the net is:

t = 1 second.

To know more about time, visit:

https://brainly.com/question/28050940

#SPJ1