Question 2: The average price for a BMW 3 Series Coupe 335i is $39,368. Suppose these prices are also normally distributed with a standard deviation of $2,367. What percentage of BMW dealers are pricing the BMW 3 Series Coupe 335i at more than the average price ($44,520) for a Mercedes CLK350 Coupe? Round your answer to 3 decimal places.
Answers
Answer:
0.015 = 1.5% of BMW dealers are pricing the BMW 3 Series Coupe 335i at more than the average price ($44,520) for a Mercedes CLK350 Coupe
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question, we have that:
\(\mu = 39368, \sigma = 2367\)
What percentage of BMW dealers are pricing the BMW 3 Series Coupe 335i at more than the average price ($44,520) for a Mercedes CLK350 Coupe?
This is 1 subtracted by the pvalue of Z when X = 44520. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{44520 - 39368}{2367}\)
\(Z = 2.18\)
\(Z = 2.18\) has a pvalue of 0.985
1 - 0.985 = 0.015
0.015 = 1.5% of BMW dealers are pricing the BMW 3 Series Coupe 335i at more than the average price ($44,520) for a Mercedes CLK350 Coupe
Related Questions
Mario needs a loan to buy a tractor for his farm. He qualified for a loan at 2 different banks.
.
First Bank of Trust
Loan Amount: $25,000
Annual Simple Interest
Rate: 6.5%
Loan Length: 4 years
What is
.
Enter your answer in the box.
.
Valor Bank
Loan Amount: $25,000
Annual Simple Interest
Rate: 4%
Loan Length: 6 years
total amount Mario will pay, including loan amount and interest, for the First Bank of Trust loan?
Answers
Answer:$31,500
Step-by-step explanation:
To calculate the total amount Mario will pay, including the loan amount and interest, for the loan from First Bank of Trust, we need to calculate the interest and add it to the loan amount.
The formula to calculate simple interest is:
Interest = (Loan Amount) x (Interest Rate) x (Loan Length)
Let's plug in the values given:
Loan Amount = $25,000
Interest Rate = 6.5% (or 0.065 as a decimal)
Loan Length = 4 years
Interest = $25,000 x 0.065 x 4 = $6,500
Now, let's calculate the total amount Mario will pay:
Total Amount = Loan Amount + Interest = $25,000 + $6,500 = $31,500
Therefore, the total amount Mario will pay, including the loan amount and interest, for the First Bank of Trust loan is $31,500.
I need expert answers for this

Answers
The last expression finally simplifies to cot β + tan α using quotient identity in trigonometric identities.
How to prove Trigonometric Identities?We want to verify the trigonometric identity;
cos (α - β)/(cos α sin β) = cot β + tan α
Now, according to trigonometric identities in mathematics, we know that;
cos (α - β) = (cos α cos β) + (sin α sin β)
Thus, plugging that back into our left hand side of the main question gives;
[(cos α cos β) + (sin α sin β)]/(cos α sin β)
Rewriting this expression by separating the denominator gives;
[(cos α cos β)/(cos α sin β)] + [(sin α sin β)]/(cos α sin β)
Using quotient identities, this can be simplified to;
cot β + tan α
Read more about Trigonometric Identities at; https://brainly.com/question/7331447
#SPJ1
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
a trader buys 200 oranges for 60 kobo and sells them at 8 for 12 kobo.what is his gain
Answers
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
Let's solve ~
Cost price for each Orange :
\(\qquad \tt \dashrightarrow \: \dfrac{60}{200} \)
\(\qquad \tt \dashrightarrow \:0.3 \: \: kobo\)
Now, Cost price for 8 oranges :
\(\qquad \tt \dashrightarrow \:0.3 \times 8\)
\(\qquad \tt \dashrightarrow \:2.4 \: \: kobo\)
And we have been given that selling price for 8 oranges is 12 kobo.
Therefore, the gain is :
\(\qquad \tt \dashrightarrow \:12 - 2.4\)
\(\qquad \tt \dashrightarrow \:9.6 \: \: kobo\)
Percentage gain is ~
\(\qquad \tt \dashrightarrow \: \dfrac{9.6}{2.4} \times 100\)
\(\qquad \tt \dashrightarrow \:4 \times 100\)
\(\qquad \tt \dashrightarrow \:400 \: \%\)
How do I do this problem

Answers
Factor the polynomial.
2x²10x + 12 =
Answers
Answer: 2(x+3)(x+2)
Step-by-step explanation:
Gallup conducted a survey from April 1 to 25, 2010, to determine the congressional vote preference of the American voters.15 They found that 51% of the male voters preferred a Republican candidate to a Democratic candidate in a sample of 5,490 registered voters. Gallup asks you, their statistical consultant, to tell them whether you could declare the Republican candidate as the likely winner of the votes coming from men if there was an election today. What is your advice
Answers
Answer:
p ( x > 2746 ) = p ( z > - 1.4552 )
= 1 - 0.072806
= 0.9272
This shows that there is > 92% of a republican candidate winning the election hence I will advice Gallup to declare the Republican candidate winner
Step-by-step explanation:
Given data:
51% of male voters preferred a Republican candidate
sample size = 5490
To win the vote one needs ≈ 2746 votes
In order to advice Gallup appropriately lets consider this as a binomial distribution
n = 5490
p = 0.51
q = 1 - 0.51 = 0.49
Hence \(n_{p}\) > 5 while \(n_{q}\) < 5
we will consider it as a normal distribution
From the question :
number of male voters who prefer republican candidate ( mean ) ( u )
= 0.51 * 5490 = 2799.9
std = \(\sqrt{npq}\) = \(\sqrt{5490 * 0.51 *0.49}\) = 37.0399 ---- ( 1 )
determine the Z-score = (x - u ) / std ---- ( 2 )
x = 2746 , u = 2799.9 , std = 37.0399
hence Z - score = - 1.4552
hence
p ( x > 2746 ) = p ( z > - 1.4552 )
= 1 - 0.072806
= 0.9272
This shows that there is > 92% of a republican candidate winning the election hence I will advice Gallup to declare the Republican candidate winner
Lilly has a piece of string that is 36 inches long. She wants to cut it into 9 equal pieces.
How long will each piece of string be?
A 4 inches
B. 6 inches
c. 25 inches
D. 27 inches
E.45 inches
Answers
Answer: A, 4 inches.
Step-by-step explanation: 36 divided by 9 is 4.
you can use the finger trick if you learned it
When the national economy goes from bad to better, market research shows changes in the sales at various types of
restaurants. Projected 2011 sales at quick-service restaurants are $164.8 billion, which was 3% better than in 2010. Projected 2011 sales at
full-service restaurants are $184.2 billion, which was 1.2% better than in 2010. How will the dollar growth in quick-service restaurants sales
compared to the dollar growth for full-service places?
Answers
The triangle and the rectangle have the same area.
All lengths are in cm.
7x + 2
a Form an equation in x.
b Solve your equation to find x.
c Work out the area of the shapes.
1
2x + 7
Answers
The length of one side of the equilateral triangle in terms of x is 6x.
To find the length of one side of the equilateral triangle in terms of x, we need to consider the perimeter of both the rectangle and the equilateral triangle.
The perimeter of a rectangle is given by the formula:
Perimeter of rectangle = 2(length + width)
In this case, the length of the rectangle is 7x cm, and the width is 2x cm. Substituting these values into the formula, we have:
Perimeter of rectangle = 2(7x + 2x) = 2(9x) = 18x
We are told that the equilateral triangle has the same perimeter as the rectangle.
Since an equilateral triangle has all sides equal, the perimeter can be calculated by multiplying the length of one side by 3.
Therefore, we have:
Perimeter of equilateral triangle = 3(side length)
Since the perimeter of the equilateral triangle is equal to the perimeter of the rectangle (18x), we can set up the equation:
3(side length) = 18x
Dividing both sides of the equation by 3, we get:
side length = 6x
Hence, the length of one side of the equilateral triangle in terms of x is 6x.
For similar question on equilateral triangle.
https://brainly.com/question/28063031
#SPJ8
The complete question may be like: A rectangle measures 2x cm by 7x cm. An equilateral triangle has the same perimeter as the rectangle. What is the length of one side of the triangle in terms of x?
y=9/4×2
sketch the graph of f and f on the same set of axes
Answers
The graph of the function \(f(x) = (9/4)x^2\) is a symmetric upward-opening parabola.
The graph represents a parabola that opens upward. As x increases, the corresponding y-values increase, forming a curved shape. The vertex of the parabola is at the origin (0,0). The graph is symmetric with respect to the y-axis, meaning that the left and right sides of the parabola are mirror images of each other.The slope of the graph gradually increases as x moves away from the origin. The steepness of the curve becomes more pronounced, indicating a faster rate of increase in y-values for larger x-values.The graph does not intersect the x-axis, indicating that there are no real roots or solutions for the equation f(x) = 0. The y-intercept of the graph is at (0, 0), and the y-values increase indefinitely as x approaches positive or negative infinity.Overall, the graph represents a quadratic function with a positive leading coefficient, resulting in an upward-opening parabolic curve. The graph has been attached.
For more questions on graph:
https://brainly.com/question/19040584
#SPJ8

This graph shows a proportional relationship.
What is the constant of proportionality?
Answers
The constant of proportionality is a crucial aspect of a proportional relationship, as it tells us how much one variable changes in relation to the other. It can be calculated from the equation of the relationship, or from the slope of the graph if it is a linear relationship.
A proportional relationship is a mathematical equation that expresses two variables that are in proportion to one another. In this type of relationship, if one variable is multiplied by a certain constant factor, then the other variable will be multiplied by the same constant factor. For example, if the cost of 3 books is $15, then the cost of 6 books will be $30. In this case, the number of books and the cost of the books are in proportion to one another.
The constant of proportionality is the constant factor by which the two variables are multiplied to obtain each other. In other words, it is the ratio between the two variables that remain constant in a proportional relationship. It can be represented by the letter k, and is calculated by dividing one variable by the other.
To find the constant of proportionality from a graph, we need to look at the slope of the line. The slope is the ratio between the change in the y-values and the change in the x-values, which is also known as the rise over run. If the graph shows a proportional relationship, then the slope will remain constant throughout the graph.
For example, if the graph shows the relationship between the number of hours worked and the amount of money earned, and the slope is 10, then the constant of proportionality is 10. This means that for every hour worked, the person earns $10. The equation for this proportional relationship can be written as y = 10x, where y represents the amount of money earned and x represents the number of hours worked.
In conclusion, the constant of proportionality is a crucial aspect of a proportional relationship, as it tells us how much one variable changes in relation to the other. It can be calculated from the equation of the relationship, or from the slope of the graph if it is a linear relationship.
For more such questions on constant of proportionality, click on:
https://brainly.com/question/1835116
#SPJ8
What is the answer?im having trouble

Answers
Answer:
130
Step-by-step explanation:
let the inside value be,x
x+30°+20°=180°(Being sum of interior angle of triangle)
or,x+50°=180°
or,x=180°-50°
or,x=130°
Now,
let the exterior angle be,a
a=x(VOA)
a=130°
Therefore the value of a is 130°.
Evaluate the function f(x)=x-6 at the given value of the variable.
b. f(5)= (Simplify your answer.)
Answers
f (x) =x-6
or, f (5)= 5-6
= - 1
A bag of 35 marbles contains equal amounts of the colors: blue, green, red, yellow, black, white, and orange. You draw 3 marbles without replacing them in the bag. What is the probability that all the marbles are blue? Give your answer as an exact fraction and reduce the fraction as much as possible.
Answers
Answer:
2/1309
Step-by-step explanation:
\(\frac{1}{7} x\frac{4}{34} x\frac{1}{11}\)
========================================================
Explanation:
There are 35 marbles and 7 colors. We have an equal amount of each color, so there are 35/7 = 5 marbles per color. We have 5 blue marbles to start.
The fraction 5/35 = 1/7 represents the probability of selecting blue.The fraction 4/34 = 2/17 is the probability of selecting another blue marble. We subtract 1 from the numerator and denominator since we did not replace the first marble chosen.The fraction 3/33 = 1/11 is the probability of selecting a third blue marble in a row.We'll multiply out those fractions to get our final answer
(1/7)*(2/17)*(1/11) = (1*2*1)/(7*17*11) = 2/1309
which is rational?3 2/3 + 3
Answers
Find the missing side of the right triangle. Leave answer in
simplest radical form.
If the legs of a right triangle are 6 and 8, then the hypotenuse
is____
A.40
B.30
C.20
D.10
Answers
Which of the following ordered pairs corresponds to an arrow on a mapping diagram that starts at 4 and ends at 1?
O (1,1)
O (1.4)
0 (4,1)
O (4,4)
Answers
Answer:
it would be 4,1
Step-by-step explanation:
because its the only one that startes with 4 and ends with 1
I am stuck please help with this graph.
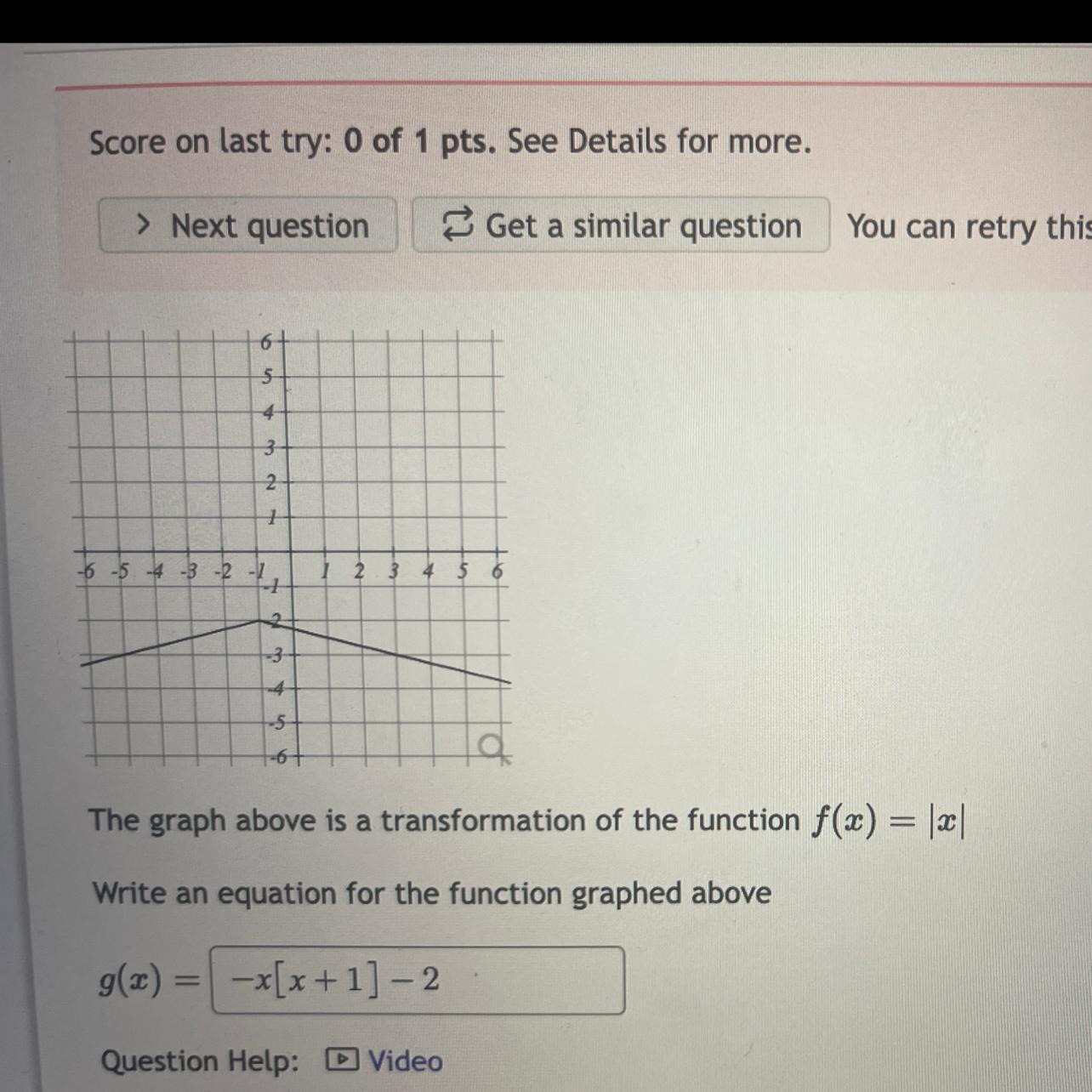
Answers
An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.
How to interpret and determine the equation of g(x)?By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;
f(x) = |x|
y = A|x + B| + C
g(x) = -1/4|x + 1| - 2
In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.
Read more on absolute value function here: brainly.com/question/28308900
#SPJ1
You are given: (i) The future lifetimes of (40) and (50) are independent. (ii) The survival function for (40) is based on a constant force of mortality, u = 0.05. (iii) The survival function for (50) is So(x) = 1 - x/10 (De Moivre's Law with w=110). Calculate the probability that (50) dies within 10 years and dies after (40). A) Less than .02 B) At least .02 but less than .04 C) At least .04 but less than .06 D) At least .06 but less than .08 E) At least.08 Select one: A. Less than .02 B. At least .02 but less than .04 C. At least.04 but less than 06 D. At least.06 but less than 08 E. At least .08
Answers
The probability that (50) dies within 10 years and dies after (40) is at least 0.02 but less than 0.04. So the answer is B. At least .02 but less than .04.
To calculate the probability that (50) dies within 10 years and dies after (40), we need to find the joint probability of the two events happening together.
Let X and Y be the future lifetimes of (40) and (50), respectively. We want to find P(Y≤10 and X<Y). Using the Law of Total Probability, we can write:
P(Y≤10 and X<Y) = ∫P(Y≤10 and X<Y|X=t) fX(t)dt
where fX(t) is the probability density function of X.
Since the force of mortality for (40) is constant, the probability density function for X is given by:
f X (t)=ue −ut
where u=0.05.
For (50), we have the survival function S(y) = 1 - y/10. So, the probability density function for Y is:
fY(y) = S'(y) = 1/10
Now, we can substitute these expressions into the integral and simplify:
P(Y≤10 and X<Y) = ∫P(Y≤10 and X<Y|X=t) fX(t)dt
= ∫∫P(Y≤10 and X<Y|X=t) fY(y)fX(t)dydt
= ∫∫P(Y≤10 and t<Y) (1/10)(0.05)e^(-0.05t)dydt
= (1/10)∫e^(-0.05t) ∫1≤y≤10 e^(0.1y) dydt
= (1/10)∫e^(-0.05t) (e - e^(-t/10)) dt
Evaluating this integral, we get:
P(Y≤10 and X<Y) ≈ 0.0286
Find out more about the Law of Total Probability
at brainly.com/question/14315459
#SPJ4
8 ft
10 ft
Find the perimeter of this figure to
the nearest hundredth.
Use 3.14 to approximate .
P = [?] ft
Notice that only half of the circle is included in the figure!
Answers
The perimeter of the figure is 4(π + 9)ft.
What is perimeter?A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length.
Given is a 2 - D figure as shown in the figure attached.
We can write the perimeter as -
P = P{rectangle} + P{semicircle}
P = 2(10 + 8) + (4π)
P = (4π) + (36)
P = 4(π + 9)
Therefore, the perimeter of the figure is 4(π + 9)ft.
To solve more questions on Perimeter, visit the link below -
https://brainly.com/question/14996609
#SPJ1
![8 ft10 ftFind the perimeter of this figure tothe nearest hundredth.Use 3.14 to approximate .P = [?] ftNotice](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/dFiczUV1VJQw8I5GGyu3EvpqmHvY45W3.png)
What is 534.8 x 17 in long multiplication?
Answers
Answer:
Step-by-step explanation: 9091.6
Answer:
9091.6
Step-by-step explanation:
How could Marc mathematically try to prove that he hit the ball near the top of the tower?While on the golf course last weekend Marc hit into the rough, landing the ball behind a tall tree. To get out of the scenario, his best option was to hit the ball high enough so it goes over the tree and hopefully comes down in the fairway for his next shot. So with a mighty swing, he hit the ball into the air and was surprised to see it hit near the top of a 300 foot tall tower that he had not noticed. The formula for this shot is h(x) = -16xsquared + 120x , where h is the height of the ball and x is the number of seconds the ball is in the air. How could Marc mathematically try to prove that he hit the ball near the top of the tower?While on the golf course last weekend Marc hit into the rough, landing the ball behind a tall tree. To get out of the scenario, his best option was to hit the ball high enough so it goes over the tree and hopefully comes down in the fairway for his next shot. So with a mighty swing, he hit the ball into the air and was surprised to see it hit near the top of a 300 foot tall tower that he had not noticed. The formula for this shot is h(x) = -16xsquared + 120x , where h is the height of the ball and x is the number of seconds the ball is in the air. How could Marc mathematically try to prove that he hit the ball near the top of the tower?
Answers
Answer:
To mathematically prove that Marc hit the ball near the top of the tower, he could use the equation h(x) = -16x^2 + 120x, where h is the height of the ball and x is the number of seconds the ball is in the air.
First, Marc would need to determine the maximum height the ball reached during its flight. This can be found by using the vertex formula, which is x = -b/2a. In this case, a = -16 and b = 120, so x = -120/(2*-16) = 3.75 seconds.
Next, Marc can substitute this value back into the original equation to find the maximum height the ball reached. h(3.75) = -16(3.75)^2 + 120(3.75) = 135 feet.
Since the tower is 300 feet tall, Marc could conclude that if the ball hit near the top of the tower, it would have reached a height close to 300 feet. Since the ball reached a maximum height of 135 feet, it is unlikely that it hit the top of the tower.
However, this calculation assumes that the tower is directly in line with Marc's shot and that the ball did not have any horizontal movement. In reality, the tower could have been to the left or right of the shot, and the ball could have had some horizontal movement, which would affect its height at impact. Therefore, this calculation can only provide a rough estimate and cannot definitively prove whether or not the ball hit near the top of the tower.
solve x/3+y/4=2
2x/3+3y/4=5
Answers
Step-by-step explanation:
please mark me as brainlest

Answer:
Step-by-step explanation:
\(\dfrac{x}{3}+\dfrac{y}{4}=2\\\\\\\text{Multiply the whole equation by the LCM of 4 , 12 which is 12}\\\\ 12*\dfrac{x}{3}+12*\dfrac{y}{4}=12*2\\\\\\4x + 3y=24 \ -------------------(i)\)
\(\dfrac{2x}{3}+\dfrac{3y}{4}=5\\\\\\\text{Multiply the whole equation by 12}\\\\12*\dfrac{2x}{3}+12*\dfrac{3y}{4}=5*12\\\\\\\)
8x + 9y = 60 -------------------------(ii)
Multiply equation (i) by (-2)
(i)*(-2) -8x -6y = -48
(ii) 8x +9y = 60 {Now add. x will be cancelled}
3y = 12 {Divide both sides by 3}
y = 12/3
y = 4
Substitute y = 4 in equation (i)
4x + 3*4 = 24
4x + 12 = 24
4x = 24 - 12
4x = 12
x = 12/4
x = 3
\(\boxed{x = 3 \ ; \ y = 4}\)
Solve the systems by elimination.
2x + 4y = -16
-2x + 2y = -2
Answers
Answer: (-2,-3)
Step-by-step explanation:
It’s me again guys!! Can anyone help me please?

Answers
=(-4)^2 - [-4]
=(16) + 4
=20
(two negatives=positive)
Hoang has worked as a nurse at Springfield General Hospital for 5 years longer than her friend Bill. Two years ago, she had been at the hospital for twice as long. How long has each been at the hospital?
Answers
5 years longer then Bill, 2x5=10.
10+2=12.
12-5=7
Hoang has be there for 12 years. Bill has for 7 years.
Mr. Heritage starts a new business, and to get it started he borrows $2 500 from a bank. If the loan is for two years, and the amount of interest for those two years is $175, what SIMPLE interest rate was he charged? (SIMPLE INTEREST: the principle and interest calculations dont change- they stay the same for the entire two year period!) BONUS- if he pays off the whole loan in the two years, what would his monthly bill be, (DON'T FORGET TO INCLUDE THE INTEREST CHARGE FOR HIS MONTHLY BILLS!!! YOU CAN ROUND YOUR CALCULATION TO THE NEAREST HUNDRETH- THAT IS, TO TWO DECIMAL PLACES...)
Answers
The rate of interest is given by the equation R = 3.5 %
What is Simple Interest?Simple interest is a method of calculating interest that ignores the impact of compounding. While interest frequently compounds throughout the course of a loan's set periods, simple interest does not. Simple interest is calculated by multiplying the principal amount by the interest rate, times the number of periods.
Simple Interest = ( Principal Amount x Rate x Time Period ) / 100
Given data ,
Let the rate of interest be represented as R
Now , the simple interest I = $ 175
The principal amount invested P = $ 2,500
The time period T = 2 years
Simple Interest = ( Principal Amount x Rate x Time Period ) / 100
Rate of Interest = (Simple Interest x 100 ) / Principal Amount x Time Period )
Substituting the values in the equation , we get
Rate of Interest R = ( 175 x 100 ) / ( 2500 x 2 )
Rate of Interest R = 17500 / 5000
Rate of Interest R = 3.5 %
Hence , the interest rate is 3.5 %
To learn more about simple interest click :
https://brainly.com/question/17282817
#SPJ1
Determine the equation of the parabola that opens to the right, has focus (-1, -3), and a focal diameter of 8.
Answers
The equation of the parabola that opens to the right, has a focus (-1, -3), and a focal diameter of 8 is y = (1/16)x²+ (10/16)x - (23/16)
To determine the equation of a parabola that opens to the right, has a focus at (-1, -3), and a focal diameter of 8
we can use the standard form of the equation for a parabola with a horizontal axis:
(x - h)² = 4p(y - k)
Where (h, k) is the vertex of the parabola and p is the distance from the vertex to the focus.
Since the parabola opens to the right, the vertex will be to the left of the focus.
Therefore, the vertex will be at (-1 - p, -3).
The focal diameter is given as 8, which means the distance between the vertex and the focus is p = 8/2 = 4.
Plugging these values into the equation, we have:
(x - (-1 - 4))² = 4 × 4 × (y - (-3))
Simplifying:
(x + 5)² = 16(y + 3)
x² + 10x + 25 = 16y + 48
Rearranging to isolate y:
16y = x² + 10x + 25 - 48
16y = x² + 10x - 23
Dividing by 16:
y = (1/16)x² + (10/16)x - (23/16)
Therefore, the equation of the parabola that opens to the right, has a focus (-1, -3), and a focal diameter of 8 is y = (1/16)x²+ (10/16)x - (23/16)
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Find the area of a circle and use 3.14 for pi

Answers
The area of the shaded region of a circle with a 100 degree angle and a radius of 3cm, using pi=3.14, is approximately 25.64 square centimeters.
To find the area of the shaded region of a circle, we need to subtract the area of the sector formed by the shaded region from the area of the whole circle.
The area of the whole circle is given by
A = πr²
where A is the area of the circle, r is the radius of the circle, and π is a mathematical constant approximately equal to 3.14 (as given in the question).
Substituting the given values, we get
A = π(3cm)²
A = 28.26 cm² (rounded to two decimal places)
Now, let's find the area of the sector formed by the shaded region.
The angle of the sector is given as 100 degrees. To find the area of the sector, we need to use the formula:
A = (θ/360)πr²
where θ is the angle in degrees, r is the radius of the circle, and π is again approximately equal to 3.14.
Substituting the given values, we get
A = (100/360)π(3cm)²
A = 2.62 cm² (rounded to two decimal places)
Finally, we can find the area of the shaded region by subtracting the area of the sector from the area of the whole circle
Shaded area = Area of circle - Area of sector
Shaded area = 28.26 cm² - 2.62 cm²
Shaded area = 25.64 cm² (rounded to two decimal places)
Therefore, the area of the shaded region of the circle is approximately 25.64 square centimeters.
To know more about Area of Circle:
https://brainly.com/question/28642423
#SPJ1
--The given question is incomplete, the complete question is given
" Find the area of a shaded region of circle and use 3.14 for pi "--