Raul works at a movie theatre. The function f(x) represents the amount of money in dollars Raul earns per ticket, where x is the number of tickets he sells. The function g(x) represents the number of tickets Raul sells per hour, where x is the number of hours he works.
f(x) = 3x2 + 16
g(x) = the square root of five times x cubed
Find f(g(x)).

Answers
The required function obtained after solving f(g(x)) will be equal to 15x³ + 16. Hence, option C is correct.
What is an equation?Mathematical expressions with two algebraic symbols on either side of the equal (=) sign are called equations.
This relationship is illustrated by the left and right expressions being equal to one another. The left-hand side equals the right-hand side is a basic, straightforward equation.
As per the functions given in the question,
f(x) = 3x² + 16
g(x) = √5x³
Now, find the function f(g(x)).
f(g(x)) = f(√5x³), [g(x) = √5x³]
f(g(x)) = 3( √5x³)² + 16 [f(x) = 3x² + 16]
So,
f(g(x)) = 3(5x³) + 16
f(g(x)) = 15x³ + 16
To know more about equation:
https://brainly.com/question/29657983
#SPJ1
Answer:
f(g(x)) = 15x^3 + 16 dollars / hour
I answered the quiz and it's correct
Related Questions
Miles got 23 out of 25 questions correct on his test. What percent did he get correct?
Answers
Answer: Miles got 92% correct on his test
Step-by-step explanation:
Answer:
92%
Step-by-step explanation:
25=100%
23=? crisco
23×100/25= 92%
a significance level for a hypothesis test is given as alpha=0.1. Interpret this value - The smallest value of alpha that you can use and still reject Null hypothesis is 0.01. - The probability of making a Type II error is 0.99. - There is a 1% chance that the sample will be biased. - The probability of making a Type I error is 0.01. With explanation, please.
Answers
The probability of making a Type I error is 0.01, which means that the power of the test is low.
The given value of alpha = 0.1 represents the level of significance chosen for a hypothesis test. It means that if the probability of obtaining the observed result or a more extreme result under the null hypothesis is less than or equal to 0.1, then we reject the null hypothesis.
The level of significance, also known as alpha, is the probability of making a Type I error. A Type I error occurs when we reject a true null hypothesis. In this case, alpha = 0.1 means that we are willing to accept a 10% chance of making a Type I error. However, the smallest value of alpha that we can use and still reject the null hypothesis is 0.01. This means that we can reduce the chance of making a Type I error to 1% by using a smaller level of significance.
On the other hand, the probability of making a Type II error is equal to 1 minus the power of the test. The power of the test is the probability of rejecting the null hypothesis when it is false. If the power of the test is low, then the probability of making a Type II error is high. Therefore, if alpha is 0.1, the probability of making a Type II error is 0.99.
The statement "there is a 1% chance that the sample will be biased" is not related to the level of significance. It is a statement about the potential for bias in the sample, which may affect the validity of the hypothesis test.
Therefore, a significance level of alpha = 0.1 means that we are willing to accept a 10% chance of making a Type I error. However, we can reduce this chance to 1% by using a smaller level of significance. The probability of making a Type II error is 0.99, which means that the power of the test is low.
To learn more about probability here:
brainly.com/question/30034780#
#SPJ11
Given the Table:
x 0 pi/6 pi/4 pi/3 pi/2
sinx 0 1/2 1/2^(1/2) ((3)^(1/2))/2 1
construct a fourth order interpolating polynomial for sin(x) and use it to approximate sin(pi/5) and find a bound on the error.
Answers
Using Lagrange interpolation, the fourth order interpolating polynomial for sin(x) is\(P(x) = (32/3)x^4 - (16/3)\pi x^3 + (4\pi ^2-8)x^2 - (4\pi ^2-16/3)\pi x,\)and the absolute error in the approximation of \(sin(\pi/5)\) is approximately 0.2788, with a bound on the error given by \(E(x) = [f^{(5)} (\zeta (x))] / 5!\) , where ξ(x) is some value between 0 and pi/2.
To construct a fourth-order interpolating polynomial for sin(x), we can use Lagrange interpolation.
The general formula for the Lagrange interpolating polynomial of degree n is:
\(P(x) = \sum [i=0 to n] f(xi)\) Π[\(j=0 to n, j \neq i] (x-xj) /\) Π\([j=0 to n, j \neq i] (xi-xj)\)
where f(xi) is the function value at the interpolation points xi.
For our problem, we want to interpolate sin(x) at the points x=0, pi/6, pi/4, pi/3, and pi/2. So we have:
f(x0) = sin(0) = 0
f(x1) = sin(pi/6) = 1/2
\(f(x2) = sin(\pi/4) = 1/2^{(1/2)}\)
\(f(x3) = sin(\pi/3) = ((3)^{(1/2)})/2\)
\(f(x4) = sin(\pi/2) = 1\)
Using these values, we can construct the Lagrange interpolating polynomial:
\(P(x) = [x(\i/6-x)(\pi/4-x)(\pi/3-x)(\pi/2-x)] / [(0(\pi/6-0)(\pi/4-0)(\pi/3-0)(\pi/2-0))]\times 0\)
\(+ [x(0-x)(\pi/4-x)(\pi/3-x)(\pi/2-x)] / [(\pi/6(0-\pi/6)(\pi/4-0)(\pi/3-0)(\pi/2-0))] \times 1/2\)
\(+ [x(0-x)(\pi/6-x)(\pi/3-x)(\pi/2-x)] / [(\pi/4(0-\pi/6)(0-\pi/4)(\pi/3-0)(\pi/2-0))] * 1/2^{(1/2)}\)
\(+ [x(0-x)(\pi/6-x)(\pi/4-x)(\pi/2-x)] / [(\pi/3(0-\pi/6)(0-\pi/4)(0-\pi/3)(\pi/2-0))] \times ((3)^{(1/2)})/2\)
\(+ [x(0-x)(\pi/6-x)(\pi/4-x)(\pi/3-x)] / [(\pi/2(0-pi/6)(0-\pi/4)(0-\pi/3)(0-\pi/2))] \times 1\)
Simplifying this expression, we get:
\(P(x) = (32/3)x^4 - (16/3)\pi x^3 + (4\pi ^2-8)x^2 - (4\pi ^2-16/3)\pi x\)
Now, to approximate sin(pi/5) using this polynomial, we substitute \(x= \pi/5\) into P(x):
\(P(\pi/5) = (32/3)(\pi/5)^4 - (16/3)\pi (\pi/5)^3 + (4\pi ^2-8)(\pi/5)^2 - (4\pi^2-16/3)\pi(\pi/5)\)
\(P(\pi/5) \approx 0.3090\)
The actual value of \(sin(\pi/5)\) is approximately 0.5878.
So the absolute error in our approximation is:
|0.3090 - 0.5878| ≈ 0.2788
To find a bound on the error, we can use the error formula for Lagrange interpolation:
\(E(x) = [f^{(n+1)}(\zeta (x))]\)
For similar question on Lagrange interpolation.
https://brainly.com/question/31396329
#SPJ11
By calculating the error bound, we can estimate the maximum error in our approximation of sin(pi/5) using the fourth-order interpolating polynomial.
To construct a fourth order interpolating polynomial for sin(x) using the given table, we can use Lagrange interpolation.
Let p(x) be the fourth order polynomial we want to find. Then,
p(x) = L0(x)sin(0) + L1(x)sin(pi/6) + L2(x)sin(pi/4) + L3(x)sin(pi/3) + L4(x)sin(pi/2)
where L0(x), L1(x), L2(x), L3(x), and L4(x) are the Lagrange basis polynomials given by:
L0(x) = (x - pi/6)(x - pi/4)(x - pi/3)(x - pi/2) / (-pi/6)(-pi/4)(-pi/3)(-pi/2)
L1(x) = (x - 0)(x - pi/4)(x - pi/3)(x - pi/2) / (pi/6)(pi/4)(pi/3)(pi/2)
L2(x) = (x - 0)(x - pi/6)(x - pi/3)(x - pi/2) / (pi/4)(pi/6)(pi/3)(pi/2)
L3(x) = (x - 0)(x - pi/6)(x - pi/4)(x - pi/2) / (pi/3)(pi/6)(pi/4)(pi/2)
L4(x) = (x - 0)(x - pi/6)(x - pi/4)(x - pi/3) / (pi/2)(pi/6)(pi/4)(pi/3)
Using these basis polynomials and the values of sin(x) from the table, we can find p(x) to be:
p(x) = (-3x^4 + 10pi^2x^2 - 15pi^2x + 8pi^2) / (16pi^2)
To approximate sin(pi/5) using this polynomial, we simply plug in x = pi/5 into p(x):
p(pi/5) = (-3(pi/5)^4 + 10pi^2(pi/5)^2 - 15pi^2(pi/5) + 8pi^2) / (16pi^2)
≈ 0.5878
To find a bound on the error of this approximation, we can use the error formula for Lagrange interpolation:
|f(x) - p(x)| ≤ M/4! * |(x - x0)(x - x1)(x - x2)(x - x3)(x - x4)|
where f(x) is the actual value of sin(x), M is the maximum value of the fourth derivative of sin(x) in the interval [0, pi/2], and x0, x1, x2, x3, and x4 are the x-values in the table.
Since sin(x) is a periodic function with period 2pi, its derivatives are also periodic with period 2pi. Therefore, we can find the maximum value of the fourth derivative of sin(x) in the interval [0, pi/2] by finding the maximum value of the fourth derivative of sin(x) in the interval [0, 2pi], which occurs at x = pi/2:
|f''''(pi/2)| = |-sin(pi/2)| = 1
Thus, we have M = 1. Plugging in the values from the table, we get:
|f(pi/5) - p(pi/5)| ≤ 1/4! * |(pi/5 - 0)(pi/5 - pi/6)(pi/5 - pi/4)(pi/5 - pi/3)(pi/5 - pi/2)|
≈ 0.0003
Therefore, our approximation of sin(pi/5) using the fourth order interpolating polynomial has an error bound of approximately 0.0003.
Given the table:
x: 0, pi/6, pi/4, pi/3, pi/2
sin(x): 0, 1/2, 1/(2^(1/2)), (3^(1/2))/2, 1
To construct a fourth-order interpolating polynomial for sin(x) and use it to approximate sin(pi/5), we can use the Newton's divided difference interpolation method. However, due to the character limit, I can't present the full computation here.
After calculating the divided differences and constructing the interpolating polynomial P(x), we can approximate sin(pi/5) by substituting x = pi/5 into the polynomial.
To find a bound on the error, we use the error formula in Newton's interpolation:
|E(x)| <= |f[x0, x1, x2, x3, x4, x]| * |Π(x - xi)|
Here, f[x0, x1, x2, x3, x4, x] is the fifth divided difference, which requires an additional point (x, sin(x)) outside the given data. Π(x - xi) is the product of differences between the interpolation point (pi/5) and the data points.
By calculating the error bound, we can estimate the maximum error in our approximation of sin(pi/5) using the fourth-order interpolating polynomial.
Learn more about polynomial at: brainly.com/question/11536910
#SPJ11
If five times a whole number increased by 3 is less than 13, then find the solution set.
Answers
Which is the sum of two or more different monomials?
Answers
Answer: Polynomial
Step-by-step explanation:
There are 75 kids at camp. After 21 kids go swimming, a counselor separated the remaining kids into 6 teams so that each team had k kids. In the tape diagram, k represents the number of kids that the counselor put into each of the 6 teams. What is the value of k?
Answers
6 * k = 54
Now, divide both sides by 6:
k = 54 / 6
k = 9
So, the value of k is 9. The counselor put 9 kids into each of the 6 teams.
please help!!!!!!!!!!!! !!!

Answers
-3/4x≤12
what are the steps to solve this??
Answers
Answer:
x≥-16
Step-by-step explanation:
-3/4x≤12
Multiply each side by -4/3, remembering to flip the inequality
-4/3 *-3/4x≥ -4/3 *12
x≥-16
Answer: x ≥ -16
Step-by-step explanation:
Divide both sides by -3/4 to get x alone.
When you divide or multiply both sides by a NEGATIVE, the inequality FLIPS.
-3/4x ≤ 12
Divide both sides by -3/4:
x ≥ -16
Hope this helps!
Given the equation A=
b−c
π
, where b=95.68±0.05 and c=43.28±0.02. What is the absolute uncertainty in A ? Select one: a. 0.05995±0.00007 b. 0.05995±0.00008 c. 05995±0.00006
Answers
The absolute uncertainty in A is approximately 0.022254. Rounding it to the same number of decimal places as A, we express the absolute uncertainty as 0.05995 ± 0.00008.
To calculate the absolute uncertainty in A, we need to determine the maximum and minimum values that A can take based on the uncertainties in b and c. The absolute uncertainty in A can be found by propagating the uncertainties through the equation.
Given:
b = 95.68 ± 0.05
c = 43.28 ± 0.02
To find the absolute uncertainty in A, we can use the formula for the absolute uncertainty in a function of two variables:
ΔA = |∂A/∂b| * Δb + |∂A/∂c| * Δc
First, let's calculate the partial derivatives of A with respect to b and c:
∂A/∂b = 1/π
∂A/∂c = -1/π
Substituting the given values and uncertainties, we have:
ΔA = |1/π| * Δb + |-1/π| * Δc
= (1/π) * 0.05 + (1/π) * 0.02
= 0.07/π
Since the value of π is a constant, we can approximate it to a certain number of decimal places. Let's assume π is known to 5 decimal places, which is commonly used:
π ≈ 3.14159
Substituting this value into the equation, we get:
ΔA ≈ 0.07/3.14159
≈ 0.022254
Therefore, the absolute uncertainty in A is approximately 0.022254.
To express the result in the proper format, we round the uncertainty to the same number of decimal places as the measured value. In this case, A is approximately 0.05995, so the absolute uncertainty in A can be written as:
ΔA = 0.05995 ± 0.00008
Therefore, the correct answer is option b. 0.05995 ± 0.00008.
Learn more about derivatives here:
https://brainly.com/question/25324584
#SPJ11
A school purchased sand to fill a sandbox on its playground. The dimensions of the sandbox in meters and the total cost of the sand in dollars are known. Which units would be most appropriate to describe the cost of the sand?
Answers
The most appropriate units to describe the cost of the sandbox would indeed be dollars.
When describing the cost of an item or service, it is essential to use the unit that represents the currency being used for the transaction. In this case, the total cost of the sand for the school's sandbox is given in dollars. To maintain consistency and clarity, it is best to express the cost in the same unit it was provided.
Using dollars as the unit for the cost allows for clear communication and understanding among individuals involved in the transaction or discussion. Dollars are widely recognized as the standard unit of currency in many countries, including the United States, where the dollar sign ($) is commonly used to denote monetary values.
Using meters, the unit for measuring the dimensions of the sandbox, to describe the cost would be inappropriate and could lead to confusion or misunderstandings. Mixing units can cause ambiguity and hinder effective communication.
Therefore, it is most appropriate to describe the cost of the sand in dollars, aligning with the unit of currency provided and commonly used in financial transactions. This ensures clarity and facilitates accurate comprehension of the cost associated with the sand purchase for the school's sandbox.
for similar questions on sandbox.
https://brainly.com/question/31290675
#SPJ8
HELP WILL GIVE BRAINLY PLZ DONT SKIP
Half of a class took Form A of a test, and half took Form B. Of the students who took form B, 39% passed. What is the probability that a randomly
chosen student took Form B and did not pass? Show ur work/explain in words what you did
A. 0.055
B 0.195
C. 0.305
D. 0.390
Answers
Answer:
C. 0.305
Step-by-step explanation:
100 - 39 = 61
.5 x .61 = .305
30.5%
if i have decent grades, but miss a lot of school
will they fail me???
Answers
A dance troupe has a total of 50 dancers split into 2 groups. The costumes worn by Group A cost $80 each, and those worn by Group B cost $90 each. If the total cost of all the costumes is $4,270, what is the total cost of the costumes worn by Group B
Answers
Answer:
2,270
Step-by-step explanation:
HOPE IT HELPED >:D
Answer:
2270 dollars
Step-by-step explanation:
You know each group has 25 dancers and then you multiply 80 by 25 to get the cost of group a. Then you just subtract 2000 from your total to get your answer.
A relationship between two quantities, normally expressed as the quotient of one divided by another. A comparison of two numbers or measurements.
Answers
The relationship that is normally expressed as the quotient of one quantity divided by another is called a ratio
The relationship that is normally expressed as the quotient of one quantity divided by another is called a ratio. A ratio is a comparison of two numbers or measurements, and it can be written in different ways.
For example, if we have two quantities A and B, the ratio of A to B can be written as
A/B
A:B
"A is to B"
The ratio of A to B tells us how many times A is contained within B, or how many units of A we would need to have to match the amount of B.
Ratios are useful in many fields, such as finance, engineering, and science, where they are used to compare and analyze different quantities and their relationships.
Learn more about ratio here
brainly.com/question/23499990
#SPJ4
What is the measure of angle b°?
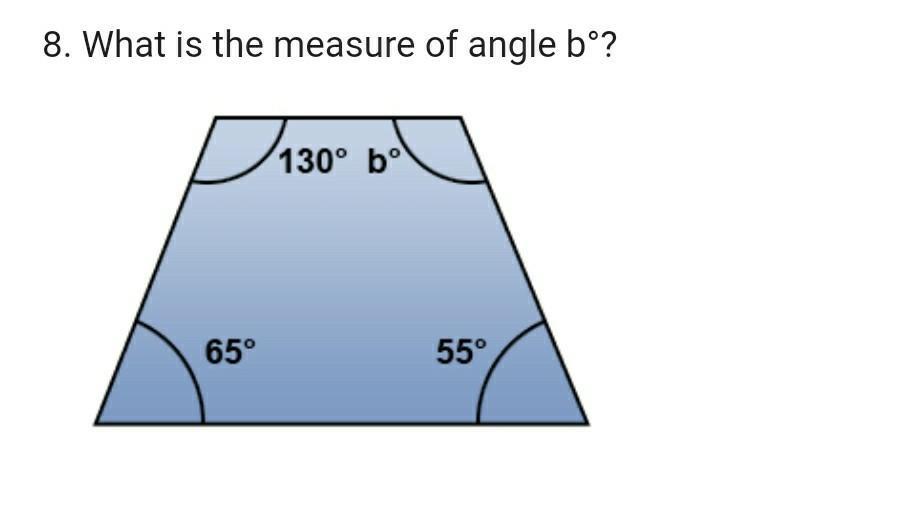
Answers
Answer:
b = 110°
Step-by-step explanation:
The sum of angles in a trapezoid is 360°
Summing the angles we get:
65°+55°+130°=250°
Then subtracting this value from 360° we get:
360°-250°=110°
Final answer of 110°
Answer:
b=110°
Step-by-step explanation:
if you add up the other angles and subtract that from 360 you get that angle
a vector points somewhere into the first quadrant. above which angle does the y-component become larger than the x-component?
Answers
Given a vector that points somewhere into the first quadrant.
We have to determine above which angle does the y-component become larger than the x-component.
The x-component and y-component of a vector pointing in the first quadrant of a Cartesian plane are given by,x = r cos θy = r sin θWhere, r is the magnitude of the vector and θ is the angle that the vector makes with the positive x-axis.
We are looking for the angle θ above which the y-component is greater than the x-component.
This is equivalent to finding the angle θ such that,y > xx cos θ < sin θx < y / sin θcos θ < sin θ / cos θ = tan θθ < tan⁻¹(y/x)Thus, the angle above which the y-component becomes greater than the x-component is θ = tan⁻¹(y/x).
Therefore, the answer is, above tan⁻¹(y/x) angle, the y-component becomes larger than the x-component.
To know more about quadrant visit:
brainly.com/question/30200246
#SPJ11
How many F-ratios must we calculate for a two-way analysis of variance?
A) 1
B) 2
C) 3
D) 4
Answers
The correct answer is D) 4.
In a two-way analysis of variance, we are examining the effects of two independent variables (or factors) on a dependent variable. We must calculate four F-ratios to test the significance of these effects: two for the main effects of each factor, and two for the interaction effect between the two factors.
The F-ratio is a statistical test that compares the amount of variability between groups to the amount of variability within groups. By calculating F-ratios for each effect, we can determine whether the differences between groups are statistically significant and whether the independent variables have a significant impact on the dependent variable.
Learn more about Two-Way Analysis here: brainly.com/question/30847840
#SPJ11
1. A manager has formulated the following LP problem. Draw the graph and find the optimal solution. (In each, all variables are nonnegative).
Maximize: 10x+15y, subject to 2x+5y ≤ 40 and 6x+3y ≤ 48.
Answers
The LP problem is to maximize the objective function 10x+15y subject to the constraints 2x+5y ≤ 40 and 6x+3y ≤ 48. By graphing the constraints and identifying the feasible region, we can determine the optimal solution.
To find the optimal solution for the LP problem, we first graph the constraints 2x+5y ≤ 40 and 6x+3y ≤ 48. These constraints represent the inequalities that the variables x and y must satisfy. We plot the lines 2x+5y = 40 and 6x+3y = 48 on a graph and shade the region that satisfies both constraints.
The feasible region is the area where the shaded regions of both inequalities overlap. We then identify the corner points of the feasible region, which represent the extreme points where the objective function can be maximized.
Next, we evaluate the objective function 10x+15y at each corner point of the feasible region. The point that gives the highest value for the objective function is the optimal solution.
By solving the LP problem graphically, we can determine the corner point that maximizes the objective function. The optimal solution will have specific values for x and y that satisfy the constraints and maximize the objective function 10x+15y.
Learn more about LP problem here:
https://brainly.com/question/17267403
#SPJ11
the figure below is a rhombus y = ?

Answers
Answer:
y = 28°
Step-by-step explanation:
The opposite angles of a rhombus are congruent.
The diagonal divides the rhombus into 2 isosceles triangles, as all sides are congruent.
Thus the triangle containing base angles y and w has vertex = 124°
Since the triangle is isosceles then the base angles are congruent , thus
y = \(\frac{180-124}{2}\) = \(\frac{56}{2}\) = 28°
Zachary purchased a computer for $1,300 on a payment plan. Three months after he purchased the computer, his balance was $910. Four months after he purchased the computer, his balance was 3780 What is an equation that models the balance y after x months?
Answers
The equation which models the balance y after x months is:
y = 1300 - 717.5x
Zachary purchased a computer for $1300
The first step is to calculate the purchase he paid after 3 months
= 1,300-910
= $390
Then the purchase after 1 month is
= $390/3
= $130 per month
The purchase made after 4 months is
= 910-3780
= -$2870
The purchase after a month is
= $-2870/4
= $-717.5 per month
Hence we get the equation as:
y = 1300 - 717.5x
Learn more about Linear equations here:
brainly.com/question/26310043
#SPJ9
What is the slope-intercept equation of the line below?
y-intercept = (0-2)
slope = -1

Answers
Answer:
y = -1x -2
Step-by-step explanation:
Simplify negative 4 and 1 over 4 − negative 9 and 1 over 2. Help ;---;
Answers
Answer:
-53/4
Step-by-step explanation:
=-4+1/4-9+1/2
=-16+1-36+2/4
=-53/4
HURRY PLEASE HELP FAST Factor 4x2 + 5x − 6.
Answers
Answer:
(X+2)(4x-3)solution,
\(4 {x}^{2} + 5x - 6 \\ = 4 {x}^{2} + (8 - 3)x - 6 \\ = 4 {x}^{2} + 8x - 3x - 6 \\ = 4x(x + 2) - 3(x + 2) \\ = (x + 2)(4x - 3)\)
Hope this helps...
Good luck on your assignment.
Answer:
4(x-1)(x+6)
Step-by-step explanation:
-1 x 6 = -6
-1+6=5
Put 4 out of the way while factoring
Then add it back once you've found your two numbers
4(x-1)(x+6)
The roots (zeros) are 1 and -6
Hope this helps!
Question 7
Which expression is equivalent to
(9–2)8?
A
-
8132
1
B
916
1
с
910
818
D help pls am I correct

Answers
Tom earned $72 walking dogs for 6 hours. How many total hours will it take tom to earn $96 in all? Solve using unit rates
Answers
Answer:
8 hours
Step-by-step explanation:
Step one:
Given data
Tom earned $72 walking dogs for 6 hours
amount earned = $72
time taken = 6 hours
Required
The time taken to earn $96
Step two:
let us find the unit rate of his earning
unit rate = 72/6
= 12 per hour
In 1 hour Tom earns $12
in x hours he will earn $96
cross multiply we have
96*1= 12x
divide both sides by 12
x= 96/12
x=8 hours
Please help me solve this

Answers
Answer:
1st pic:
x = 49
top angle = 45
bottom angle = 108
far right angle = 27 degrees
2nd pic:
angle 1 = 88 degrees
angle 2 = 57 degrees
angle 3 = 35 degrees
angle 4 = 145 degrees
Step-by-step explanation:
1st pic:
you can find the far right angle by taking 153 and subtracting it from 180:
⇒ 180 - 153 = 27 degrees
you can find x by the following equation ⇒ x - 4 + 2x + 10 + 27 = 180
combine like terms ⇒ 3x + 33 = 180
subtract 33 from each side ⇒ 3x + 33 - 33 = 180 - 33 ⇒ 3x = 147
divide 3 on each side: ⇒ \(\frac{3x}{3} = \frac{147}{3}\)
x = 49
to find the top and bottom angles, substitute 49 for x:
top angle : x - 4
49 - 4 = 45 degrees
bottom angle: 2x + 10
2 x 49 + 10 = 108 degrees
2nd pic:
angle 1:
⇒ 180 - 92 = 88 degrees
angle 2:
⇒ 180 - 123 = 57 degrees
angle 3:
⇒ 180 - (88 + 57) = 35 degrees
angle 4:
⇒ 180 - 35 = 145 dgerees
please help i don’t understand these

Answers
A student provided the steps for solving an equation. Which statement describes the error in the solution? Equation: 8-1=3(4-5a) Solution: 16-a-6(4-5a) 16-a-24-5a 16+4a=24 4a=8 a=2 (step 1) (step 2) (step 3) (step 4) (step 5) In step 2, the Distributive Property was applied incorrectly. In step 5, the Multiplication Property of Equality was applied incorrectly. In step 1, the Multiplication Property of Equality was applied incorrectly. In step 3, the Addition Property of Equality was applied incorrectly.
Answers
The error in the solution is that, In step 2, the Distributive Property was applied incorrectly.
What is meant by Solving Equations?Equations are mathematical expressions consisting of two or more variables and constants on two sides connected by an equal to sign.
Solution of the equation is the value of the variable that the equation holds true.
Given equation is,
8 - \(\frac{a}{2}\) = 3 (4 - 5a)
Using the multiplication property of equality, multiplying whole equation by 2,
(2 × 8) - a = 6 (4 - 5a)
16 - a = 6 (4 - 5a)
Distributive property states that, for three numbers or expressions, a, b and c,
a (b + c) = ab + ac
Applying that,
6 (4 - 5a) = (6 × 4) - (6 × 5a) = 24 - 30a
But the student didn't multiply 6 with 5a, and thus he got 24 - 5a in step 2.
Hence the incorrect step is step 2 because of incorrect use of distributive property.
To learn more about Solving Equations, click on the link :
https://brainly.com/question/29050831
#SPJ9
Your question is a bit confusing. The complete question with an image is given below.
A student provided the steps for solving an equation. Which statement describes the error in the solution?
Equation : 8 - \(\frac{a}{2}\) = 3 (4 - 5a)

In the figure below, MN | KL and are intersected by transversals ML and KN M 1551 What is the measure of , XMN?
130°
85°
55°
50°

Answers
Answer:
∠ XMN = 50°
Step-by-step explanation:
∠ XNM and ∠ XKL are alternate angles and are congruent, then
∠ XNM = 35°
The sum of the 3 angles in a triangle = 180° , so
∠ XMN = 180° - (95 + 35)° = 180° - 130° = 50°
ameson has the following sources of income: Sole proprietorship income $40,000 General partnership operating income $5,000 Interest income from general partnership $1,200 What is the amount of self-employment tax Jameson owes
Answers
Jameson's self-employment tax amount depends on the income from his sole proprietorship and general partnership. Self-employment tax is calculated based on the net earnings from self-employment, which include both sole proprietorship income and a portion of general partnership income.
To determine the self-employment tax owed by Jameson, he first needs to calculate his net earnings from self-employment. This is done by combining the income from his sole proprietorship ($40,000) and a portion of the general partnership operating income ($5,000).
Since Jameson is a general partner, he is subject to self-employment tax on his distributive share of the partnership income.
Assuming his distributive share is 50% (for illustrative purposes), his net earnings from self-employment would be $40,000
(sole proprietorship income) + $2,500 (50% of general partnership operating income) = $42,500.
Jameson would then apply the self-employment tax rate, which is currently 15.3% for the year 2021, to his net earnings from self-employment ($42,500) to calculate the amount of self-employment tax he owes.
To learn more about sole proprietorship income click here: brainly.com/question/32293509
#SPJ11