Review the results of Exercises. What is the effect of decreasing the sample size?
Exercise
Conduct a test to determine whether the two classifications L and M are independent, using the data in the accompanying cross-classification table. (Use α = .05.)
Repeat Exercise using the following table:
Answers
The classifications L and M are independent.
How L and M classifications are independent accompanied by cross-classification table?As the sample size decreases, the accuracy of the results of an experiment can decrease or become less reliable.
When the sample size decreases, the accuracy of the experiment's results can decrease or become less reliable. The smaller the sample size, the less representative it is of the population being studied. As a result, it will be less probable that the sample provides an accurate depiction of the entire population.
Use α = .05 and Independent; Performing the hypothesis test for independence of two classifications L and M, using the data from the given cross-classification table with α = .05 and independent: Null hypothesis: There is no relationship between the two classifications Alternative hypothesis: There is a relationship between the two classifications The formula for calculating the chi-square test statistic is: χ² = ∑(O - E)²/E, where O = observed frequency in each category, E = expected frequency in each category.
We must first calculate the expected frequency for each cell. We use the formula E = (row total * column total) / grand total expected frequencies for the given table is: Thus, the chi-square test statistic, calculated as per the formula above, is χ² = 0.942With α = .05 and degrees of freedom = (2 - 1) * (2 - 1) = 1, the critical value of χ² is 3.84.As the calculated value of χ² = 0.942 < 3.84, it falls in the acceptance region. Therefore, we cannot reject the null hypothesis. Therefore, we may conclude that the classifications L and M are independent.
Repeat the exercise using the given table. We repeat the same procedure to calculate the expected frequencies for each cell and then calculate the chi-square test statistic as follows: Expected frequencies for the given table is: Thus, the chi-square test statistic, calculated as per the formula above, is χ² = 0.933With α = .05 and degrees of freedom = (2 - 1) * (2 - 1) = 1, the critical value of χ² is 3.84.As the calculated value of χ² = 0.933 < 3.84, it falls in the acceptance region. Therefore, we cannot reject the null hypothesis. Therefore, we may conclude that the classifications L and M are independent.
Learn more about cross-classification
brainly.com/question/28505844
#SPJ11
Related Questions
Let A = {2,4,6,8,10,12} B = {3,6,9,12,15,18} C = {0,6,12,18} Find C-A. none of the choices {2,3,4,6,8,9,10,12} O {2,4,8,10) {0,18}
Answers
the correct choice is {0, 18}. These elements are unique to set C and do not appear in set A.
To find the set difference C - A, we need to remove all elements from A that are also present in C. Let's examine the sets:
C = {0, 6, 12, 18}
A = {2, 4, 6, 8, 10, 12}
We compare each element of A with the elements of C. If an element from A is found in C, we exclude it from the result. After the comparison, we find that the elements 2, 4, 8, 10 are not present in C.
Thus, the set difference C - A is {0, 18}, as these are the elements that remain in C after removing the common elements with A.
Therefore, the correct choice is {0, 18}. These elements are unique to set C and do not appear in set A.
To know more about Element related question visit:
https://brainly.com/question/13266399
#SPJ11
question 2 help me please
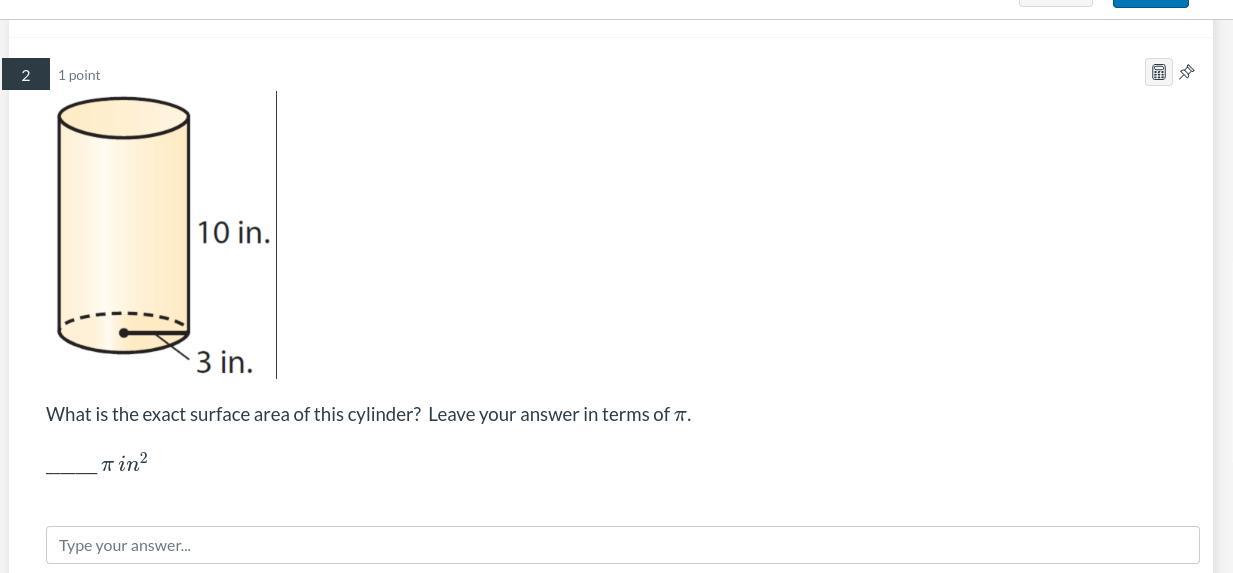
Answers
Answer:
90π in²
Step-by-step explanation:
Surface area of cylinder:r = 3 in
h = 10 in
\(\sf \boxed{\text{\bf Surface area of cylinder =$\pi r^2h$}}\)
\(= \pi 3*3*10\\\\= 90 \pi \ in^2\)
In this question it is given that the radius of a cylinder is 3 inches. The height of the cylinder is 10 inches. We are asked to calculate the surface area of the cylinder in terms of π .
Radius = 3 inches
Height = 10 inches
We know,
\( \star \: \small \boxed{\rm{ Surface \: area \: of \: a \: cylinder = πr²h}}\)
Substituting the values we get
\( \small\sf{ Surface \: area \: of \: a \: cylinder = π × 3² × 10}\)
\( \small\rm{ Surface \: area \: of \: a \: cylinder = π × 3 \times 3 × 10}\)
\( \small\rm Surface \: area \: of \: a \: cylinder = π × 90\)
\( \small\sf{ Surface \: area \: of \: a \: cylinder = \bf{90 π \: inches²}}\)
I don’t understand the questions

Answers
The solutions to the expressions using laws of exponents are;
17) y^(19/28)
18) 1/a^(5/9)
How to use Laws of Exponents?The product rule of exponents states that "To multiply two expressions with the same base, add the exponents while keeping the base the same". Thus;
y² × y³ = y²⁺³
= y⁵
17) y^(3/7) × y^(1/4)
Applying product rule of exponents gives;
y^(³/₇ + ¹/₄)
= y^(19/28)
18) The negative exponent rule states that: To convert any negative exponent into positive exponent, the reciprocal should be taken." Thus;
x⁻³ = 1/x³
Thus;
a^(-5/9) = 1/a^(5/9)
Read more about Laws of Exponents at; https://brainly.com/question/11761858
#SPJ1
True or False, the chance of flipping heads on a coin 3 times in a row is 1/2
Answers
true flip a coin it's fifty fifty
Answer:
False
Step-by-step explanation:
Each toss is an independent event, so the probability of three tosses of heads in a row is the product of the three probabilities..
Each probability of heads is
p(heads) = 1/2
p(heads, heads, heads) = p(heads) * p(heads) * p(heads) = 1/2 * 1/2 * 1/2 = 1/8
Answer: False
Help please help help please help help me

Answers
Answer:
calm down 5x = 40 x = 8
40+40+3y-8=180
3y=108
y = 36
can you help me in something please?
Determine the equivalent system for the given system of equations.
4X - 5y = 2
3X - Y = 8
A) 4x - 5y = 2
10x - 7y = 18
B) 4x - 5y = 2
3x - 8y = 4
C) 4x - 5y = 2
10x + 3y = 15
D) 4x - 5y = 2
7x + 6y = 10
Answers
Answer:
primera ×:4 mas 3y,yE R. es la repuesta de la primera
If Kiri has 17 part-time members this month, how many full-time members does she need according to your equation?
Answers
Answer:
5050 = 225f + 125p
If p = 17 this month, then, f = 13
Step-by-step explanation:
Kiri owns a coworking space that has two primary types of memberships, full time and part-time. In order to pay her bills each month (rent on the building, electricity, internet, and so on) she needs to make $5050. Full-time memberships (f) cost $225 per month, and part-time memberships (p) cost $125 per month.
If Kiri has 17 part-time members this month, how many full-time members does she need according to your equation?
Total cost = $5050
cost of full-time memberships = $225
number of full time members = f
cost of part-time memberships = $125
number of part-time members = p
Total cost = cost of full-time memberships * number of full time members + cost of part-time memberships * number of part-time members
5050 = 225f + 125p
If p = 17 this month,
5050 = 225f + 125p
5050 = 225f + 125(17)
5050 = 225f + 2,125
5050 - 2,125 = 225f
2,925 = 225f
f = 2,925/225
f = 13
number of full time members = f = 13
If p = 17 this month, then, f = 13
-0.6 ÷ 3/4
1. 0.8
2. -0.8
3. -0.15
4. 0.15
Answers
How do you use the definition of continuity and the properties of limits to show that the function h(t) = (2t-3t^2)/(1+t^3) is continuous at the given number a=1?
Answers
The function h(t) = (2t-3t^2)/(1+t^3) is continuous at a=1 because the limit of h(t) as t approaches 1 is equal to h(1).
First, we need to show that the limit of h(t) as t approaches 1 is equal to h(1).
Since h(t) = (2t-3t^2)/(1+t^3), we can rewrite the limit of h(t) as t approaches 1 as:
lim t->1 (2t-3t^2)/(1+t^3) = lim t->1 (2-3t)/(1+t^3)
We can now use the properties of limits to evaluate the limit.
Substituting t=1 into the expression for the limit, we have:
lim t->1 (2-3t)/(1+t^3) = (2-3(1))/(1+(1)^3) = -1/(2)
Now, we can use the definition of continuity to show that h(t) is continuous at a=1.
Since the limit of h(t) as t approaches 1 is equal to h(1), then h(t) is continuous at a=1.
Thus, we have successfully shown that the function h(t) = (2t-3t^2)/(1+t^3) is continuous at a=1.
learn more about function here
https://brainly.com/question/12431044
#SPJ4
Find the average value of f(x) = -3/x+ 5 7x over the interval [0, 3). Submit an exact answer using fractions and/or roots if needed. Provide your answer below: The average value of f(x) is
Answers
The given function is: f(x) = -3/x + 57xTo find the average value of f(x) over the interval [0, 3),we can use the following formula: where f(x) is the given function.
Let's calculate the definite integral of the given function f(x):
We can substitute upper limit 3 in the function to find the integral as follows: ∴ ∫₀³ f(x) dx
= [ -3 ln|x| + 5x²/2 ] ₀³
= [ -3 ln|3| + 5(3²/2) ] - [ -3 ln|0| + 5(0²/2) ]
= [ -3 ln|3| + 22.5 ]
Therefore, the average value of f(x) over the interval [0, 3) is given by: =
= [-3 ln|3| + 22.5]/(3 - 0)
= [-3 ln|3| + 22.5]/3
Now, let's convert the natural logarithm of 3 into a decimal and simplify the fraction.
≈ [-3(1.0986) + 22.5]/3
= [-1.650 + 22.5]/3
= 20.85/3
= 6.95
Answer: The average value of f(x) is 6.95.
To know more about the integral visit:
https://brainly.com/question/31059545
#SPJ11
help me on math pleaseee

Answers
Answer:
its too blurry
Step-by-step explanation:
Answer:
slope intercept form is -2/3 for the first one
When you try to find the most appropriate input probability distribution in a simulation model, you first have to choose the most appropriate family, and then you have to select the most appropriate member of that family.
True
False
Answers
The statement 'When you try to find the most appropriate input probability distribution in a simulation model, you first have to choose the most appropriate family, and then you have to select the most appropriate member of that family' is generally true because in simulation modeling, input probability distributions are used to represent uncertain or random factors in the system being modeled.
These distributions are often classified into different families, such as normal, exponential, uniform, and so on, based on their properties and mathematical characteristics.
When selecting an appropriate distribution for a simulation model, it is important to first identify the family of distributions that best represents the underlying random process being modeled.
For example, if the data is symmetric and bell-shaped, then the normal distribution might be a suitable family to consider. However, if the data is non-negative and skewed, then the exponential or gamma distribution might be more appropriate.
Once the appropriate family of distributions is selected, the next step is to identify the most appropriate member or parameter values of that family that best fit the data being modeled.
This often involves using statistical methods to estimate the parameters of the distribution based on historical data or expert knowledge.
To know more about probability distribution here:
https://brainly.com/question/14210034#
#SPJ11
What is the answer this math problem. -6+ -(8x - 3)
Answers
Answer:
x = -3÷8
or x = -0.375
Explanation:
-6+ -(8x-3)= -6-8x+3
= -8x -3
-8x-3= 0
-8x = 3
8x = -3
x = -3÷8
what is the value of f(x) = 2•2 ^x for f(-2)?
Answers
Answer:
Sorry icant help
Step-by-step explanation:
i never did this before
please help it asks: the graph below represents which of the following functions

Answers
can someone please explain
how to do this

Answers
Answer:
93
Step-by-step explanation:
A + B +C = 180
75+51 + C =180
126 +C =180
C = 180-126 = 54
DCB : ACD = 2:1
DCB = 2x
ACD = x
2x+x=54
3x = 54 ; x = 54/3 = 18
DCB = 2x = 2 x 18 = 36
dcb + dbc + bdc = 180
51 + 36 + bdc = 180
87 + bdc = 180 ; bdc = 180 - 87 = 93
I hope im right!!
Answer:
the answer is 93°
Step-by-step explanation:
As you know that in a triangle,
angle1+angle2+angle3 = 180°
hence,
angle ABC + angle BAC + angle DCB + angle ACD ( Angle DCB + angle ACD = angle BCA) = 180°
75°+51°+2x+1x (let the ratio be x) = 180°
126°+3x = 180°
3x = 54°
x = 18°
2x = 36° = angle DCB
In triangle DCB,
51°+36°+angle BCD = 180°
angle BCD = 180°- 87°
Hence, angle BCD = 93°
Find constants a and b such that the graph of f(x) = x3 + ax2 + bx will have a local max at (-2, 9) and a local min at (1,7).
Answers
The constants \(\(a\) and \(b\) are \(a = \frac{3}{2}\) and \(b = -6\).\)
How to find \(\(a\) and \(b\)\) for local extrema?To find the constants \(a\) and \(b\) such that the graph of \(\(f(x) = x^3 + ax^2 + bx\)\) has a local maximum at (-2, 9) and a local minimum at (1, 7), we need to set up a system of equations using the properties of local extrema.
1. Local Maximum at (-2, 9):
At the local maximum point (-2, 9), the derivative of \(\(f(x)\)\) should be zero, and the second derivative should be negative.
First, let's find the derivative of \(\(f(x)\):\)
\(\[f'(x) = 3x^2 + 2ax + b\]\)
Now, let's substitute \(\(x = -2\)\) and set the derivative equal to zero:
\(\[0 = 3(-2)^2 + 2a(-2) + b\]\)
\(\[0 = 12 - 4a + b \quad \text{(Equation 1)}\]\)
Next, let's find the second derivative of\(\(f(x)\):\)
\(\[f''(x) = 6x + 2a\]\)
Now, substitute \(\(x = -2\)\) \(\[f''(-2) = 6(-2) + 2a < 0\]\) and ensure that the second derivative is negative:
\(\[f''(-2) = 6(-2) + 2a < 0\]\[-12 + 2a < 0\]\[2a < 12\]\[a < 6\]\)
2. Local Minimum at (1, 7):
At the local minimum point (1, 7), the derivative of \(\(f(x)\)\) should be zero, and the second derivative should be positive.
Using the derivative of \(\(f(x)\)\) from above:
\(\[f'(x) = 3x^2 + 2ax + b\]\)
Now, let's substitute \(\(x = 1\)\) and set the derivative equal to zero:
\(\[0 = 3(1)^2 + 2a(1) + b\]\[0 = 3 + 2a + b \quad \text{(Equation 2)}\]\)
Next, let's find the second derivative of\(\(f(x)\):\)
\(\[f''(x) = 6x + 2a\]\)
Now, substitute\(\(x = 1\) \\\) and ensure that the second derivative is positive:
\(\[f''(1) = 6(1) + 2a > 0\]\[6 + 2a > 0\]\[2a > -6\]\[a > -3\]\)
To summarize, we have the following conditions:
\(Equation 1: \(0 = 12 - 4a + b\)Equation 2: \(0 = 3 + 2a + b\)\)
\(\(a < 6\) (to satisfy the local maximum condition)\(a > -3\) (to satisfy the local minimum condition)\)
Now, let's solve the system of equations to find the values of a and b
From Equation 1, we can express b in terms of a:
\(\[b = 4a - 12\]\)
Substituting this expression for b into Equation 2, we get:
\(\[0 = 3 + 2a + (4a - 12)\]\[0 = 6a - 9\]\[6a = 9\]\[a = \frac{9}{6} = \frac{3}{2}\]\)
Substituting the value of \(a\) back into Equation 1, we can find b
\(\[0 = 12 - 4\left(\frac{3}{2}\right) + b\]\[0 = 12 - 6 + b\]\[b = -6\]\)
Therefore, the constants a and b that satisfy the given conditions are\(\(a = \frac{3}{2}\) and \(b = -6\).\)
Learn more about: extrema
brainly.com/question/2272467
#SPJ11
Please I need help Graph the following polynomials finding all key features including x-intercepts, y-intercept, máximums, end behavior, and multiplicity

Answers
Given:
There are given the polynomial equation:
\(f(x)=(x-2)(x+2)^3(x+6)\)Now,
We need to find the value for the x-intercept, y-intercept, maximum, end behaviors, and multiplicity.
So,
First, find the x-intercept and y-intercept:
To find the x-intercept put 0 for y and to find the y-intercept 0 for x.
Then,
The x-intercept and y-intercept are shown below:
\(\begin{gathered} f(x)=(x-2)(x+2)^{3}(x+6) \\ x-intercept:(2,0),(-2,0),(-6,0) \\ y-intercept:(0,-96) \end{gathered}\)Now,
The value of maximum and minimum, end behavior and multiplicity is shown below:
\(\begin{gathered} End\text{ behaviour: falls to the left and rise to the right} \\ Multiplicity:1,3,1 \end{gathered}\)Final answer:
Hence, the value of x-intercept, y-intercept, end behaviour and multiplicity are shown below:
\(\begin{gathered} x-\imaginaryI ntercept:(2,0),(-2,0),(-6,0) \\ y-intercept:(0,-96) \\ End\text{behav}\imaginaryI\text{our: falls to the left and rise to the right} \\ Mult\imaginaryI pl\imaginaryI c\imaginaryI ty:1,3,1 \end{gathered}\)Find the fourth degree polynomial function with zeros 6,-6,6i
Answers
Answer:
See below
Step-by-step explanation:
6 is a solution to x-6=0, -6 is a solution to x+6=0, and 6i is a solution to x^2+36=0. So, we can do (x-6)(x+6)(x^2+36) to get (x^2-36)(x^2+36) which gets us x^4-1296. Therefore, the fourth degree polynomial with zeroes 6, -6, 6i is x^4-1296
Identify the absolute value of: |4|
A. - 2
B. - 4
C. 2
D. 4
Answers
Answer:
D. 4
Step-by-step explanation:
The absolute value of anything is just the positive form... it doesn't mater if it was originally a positive or negative.
(q5) Determine whether these lines are parallel, perpendicular, or neither.

Answers
These slopes are negative reciprocals of each other (3 x -1/3 = -1). The lines are perpendicular.
When we are asked to find out if the two lines are parallel, perpendicular, or neither, we will use the slopes of the lines.
If the slopes of the lines are equal, the lines are parallel. If the slopes are negative reciprocals of each other, the lines are perpendicular.
If neither of these conditions is met, the lines are neither parallel nor perpendicular.
The slope of the line with equation y = 3x + 1 is 3. The slope of the line with equation y = -1/3x + 2 is -1/3.
To learn more about : slopes
https://brainly.com/question/16949303
#SPJ8
Kiaya has to have at least $100 in her checking account to avoid a fee from the bank. She has $376 in her account now. Each week, she makes a $25 withdrawal. For how many weeks can she make this withdrawal and avoid a fee?
Answers
Answer:
$500 a week
Step-by-step explanation:
Hope I can help.
Kiaya can make a $25 withdrawal for 11 weeks without incurring a fee.
What is the division operation?In mathematics, divides left-hand operands into right-hand operands in the division operation.
Kiaya needs to have at least $100 in her checking account to avoid a fee from the bank. She has $376 in her account now, so she can make $376 - $100 = $276 worth of withdrawals before she will be charged a fee.
Each week, she makes a $25 withdrawal.
To determine the number of weeks she can make this withdrawal before being charged a fee, we divide the total amount she can withdraw ($276) by the amount she withdraws each week ($25).
So, Kiaya can make $276 / $25 = 11 withdrawals before she will be charged a fee.
Therefore, she can make a $25 withdrawal for 11 weeks without incurring a fee.
To learn more about the division operation click here :
brainly.com/question/25870256
#SPJ2
Solve for θ to the two decimal places, where 0≤θ≤2π. Show its CAST rule diagram as well. a) 12sin^2θ+sinθ−6=0 b) 5cos(2θ)−cosθ+3=0
Answers
The solutions for θ in the given equations are as follows:
a) θ ≈ 1.24, 4.40 (in radians)
b) θ ≈ 0.89, 2.01 (in radians)
How can we solve the equation 12sin^2θ+sinθ−6=0 for θ to two decimal places?a) To solve the equation 12sin^2θ+sinθ−6=0, we can use the quadratic formula with sinθ as the variable. Solving the quadratic equation will give us the values of sinθ, and then we can use the inverse sine function to find the values of θ.
By applying these steps, we find that θ ≈ 1.24, 4.40 (in radians).
b) To solve the equation 5cos(2θ)−cosθ+3=0, we can simplify the equation by applying the double-angle formula for cosine and rearranging terms.
This leads to a quadratic equation in cosθ. Solving the quadratic equation will give us the values of cosθ, and then we can use the inverse cosine function to find the values of θ. By following these steps, we find that θ ≈ 0.89, 2.01 (in radians).
Learn more about equations
brainly.com/question/14686792
#SPJ11
A kilobyte is 2*10 bytes and a megabyte is 2*20 bytes. How many kilobytes are in a megabyte?
Answers
Answer:
10KB = 1MB
Step-by-step explanation:
Since 1KB => 2*10bytes
1MB => 2*20bytes
Therefore 10KB => 1MB
At a particular restaurant, each slider has 225 calories and each chicken wing has 70 calories. A combination meal with sliders and chicken wings has a total of 7 sliders and chicken wings altogether and contains 1110 calories. Write a system of equations that could be used to determine the number of sliders in the combination meal and the number of chicken wings in the combination meal.
Answers
Answer:
The appropriate equation for the above mentioned conditon would be
x+y=7
225x+70y=1110
Step-by-step explanation:
As mentioned in the question the meals contain just two delicacies (i.e. sliders and chicken wings)
Let the number of Sliders be represented by “x”
Let Number of Chicken wings be represented as “y”
As given in the question the total number of sliders and chicken wings equals 7
Hence x + y =7… Equation 1
Further, it is mentioned that each slider carries worth 225 calories of energy and chicken wing carries 70 calories of energy. Total calorie of a meal which contains sliders and wings is 1110 calories.
Thus, Total energy carried by sliders individually = total sliders* energy carried by one slider= 225x
Similarly, Total energy carried by wings individually = total chicken wings* energy carried by one wing= 70y
Thus 225x+70y=1110
Is the graphed function linear?
Yes, because every input has only one output.
Yes, because there are no negative values for inputs.
No, because the curve indicates that the rate of change is not constant.
No, because the outputs are increasing as the inputs increase.
Answers
It is not linear the curve indicates that the rate of change is not constant , Option C is the correct answer.
The complete question is
A coordinate plane showing eight plotted points in a curved line. The points are at, (1, 0), (2, 25), (3, 50), (4, 80), (5, 190), (6, 200), (7, 275), (8, 400). Is the graphed function linear?
1.Yes, because each input value corresponds to exactly one output value.
2. Yes, because the outputs increase as the inputs increase.
3.No, because the graph is not continuous.
4.No, because the curve indicates that the rate of change is not constant.
What is a linear Function ?A linear function is what can be represented by the equation y= mx +c , where m is the slope and c is the intercept on y axis.
On plotting the graph of the given data points.
It can be seen from the plot that
it is not linear the curve indicates that the rate of change is not constant , Option C is the correct answer.
To know more about Linear Function
https://brainly.com/question/21107621
#SPJ1

Anthony measured a line to be 16 inches long. If the actual length of the line is 15.6 inches, then what was the percent error of the measurement, to the nearest tenth of a percent?
Answers
Answer:
2.6%
Step-by-step explanation:
You want to know the measurement error when an actual length of 15.6 inches is measured as 16 inches.
Error percentThe percentage error can be found from ...
(measured/actual -1) · 100%
(16/15.6 -1) · 100% ≈ 2.6%
The error in the measurement is about 2.6%.
__
Additional comment
The positive value of the error percentage means the measurement is higher than the actual amount by that percentage.
Please note that we are not multiplying the error fraction by 100. Rather, we are multiplying it by 100% = 1. The purpose is to move the decimal point and add a % symbol to the decimal fraction.

I need help pls !!!!

Answers
Answer:
angle 3 im prob wrong
Step-by-step explanation:
Pleases help ASAP!!!
Consider the function f(x)=sqrt x-4+9 for the domain [4, infinity).
Find f^-1(x), where f^-1 is the inverse of f.
Also state the domain of f^-1 in interval notation.
Answers
Answer: To find the inverse function of f(x), we need to solve for x in terms of f(x). We start by writing:
y = f(x) = sqrt(x - 4) + 9
We then swap x and y and solve for y:
x = sqrt(y - 4) + 9
x - 9 = sqrt(y - 4)
(x - 9)^2 = y - 4
y = (x - 9)^2 + 4
So the inverse of f(x) is f^(-1)(x) = (x - 9)^2 + 4.
To find the domain of f^(-1)(x), we need to consider the range of f(x), which is [5, infinity). Since the inverse function swaps the roles of x and y, the domain of f^(-1)(x) is [5, infinity). So in interval notation, the domain of f^(-1)(x) is [5, infinity).
Step-by-step explanation:
Swim floats are on sale at sam’s shop. They are marked 30% off of the original price of 18.00. How much will the float cost
Answers
Answer:
the cost is now $5.40
Step-by-step explanation:
if 18.00 is 100%, and we need to find the new price we need to make 30% into a decimal. which is 0.3. then we multiply 0.3 times 18.00, and that equals 5.4, but since we are dealing with money the answer would be $5.40.
we multiply if we are trying to find the new amount and we divide to find the old amount.