Rewrite all equations to slope-intercept form.
2x+6y=2
4x+9y=15
2x+6y=18
3x+2y=5
Answers
Slope intercept form of all equations.
1.
2x+6y=2
6y = -2x+2
divide by 6 on both sides
6y/6 = -2x/6 + 2/6
y = (-1/3)x+1/3.
2.
4x+9y=14
9y = -4x + 14
divide by 9 on both sides
9y/9 = (-4/9)x + 14/9
y = (-4/9)x + 14/9
3.
2x+6y=18
6y = -2x+18
divide by 6 on both sides
6y/6 = -2/6x+18/6
y = (-1/3)x + 3
4.
3x+2y=5
2y = -3x+5
divide by 2 on both sides
2y/2 = -3/2x + 5/2
y = (-3/2)x + 5/2.
Learn more about the slope intercept form here:
https://brainly.com/question/24683642
#SPJ1
Related Questions
Which ordered pair is a reflection of (3, 7) across the x-axis?
(-3, 7)
(3, -7)
(-3, -7)
(7, -3)
Answers
Answer: B (3,-7)
Step-by-step explanation:
When we reflect something across the x-axis, we just multiply the y-coordinate by -1. When trying this out with our y coordinate, we get:
7 * -1 = -7
So we get:
(3,-7)
True/false: the slope of the simple linear regression model represents the average change in the value of the dependent variable (y) per unit change in the independent variable (x).
Answers
The statement the slope of the simple linear regression model represents the average change in the value of the dependent variable (y) per unit change in the independent variable (x) is true because the slope represents the rate of change between the variables.
The slope in a simple linear regression model represents the change in the dependent variable (y) corresponding to a one-unit change in the independent variable (x). It measures the average rate of change between the variables. By calculating the slope coefficient, we can determine the average increase or decrease in the value of y for each unit increase in x.
For example, if the slope coefficient is 2, it means that, on average, for every one-unit increase in x, the value of y increases by 2 units. Similarly, if the slope coefficient is -1, it means that, on average, for every one-unit increase in x, the value of y decreases by 1 unit.
Therefore, the slope of the simple linear regression model quantifies the average change in the value of the dependent variable (y) for each unit change in the independent variable (x).
To know more about linear regression, refer here:
https://brainly.com/question/13328200
#SPJ11
a plane is defined by any three points that are in the plane. if a plane contains the points p(1,0,0), q(1,1,1), and r(2,−1,3), then find a vector orthogonal to the plane.
Answers
A vector orthogonal to the plane defined by points P(1,0,0), Q(1,1,1), and R(2,-1,3) is:
(4, 1, -1).
To find a vector orthogonal to the plane defined by points P(1,0,0), Q(1,1,1), and R(2,-1,3), follow these steps:
1. Find two vectors that lie in the plane by subtracting the coordinates of the given points. Let's use PQ and PR:
PQ = Q - P = (1-1, 1-0, 1-0) = (0, 1, 1)
PR = R - P = (2-1, -1-0, 3-0) = (1, -1, 3)
2. Calculate the cross product of PQ and PR to obtain a vector orthogonal to the plane:
PQ x PR = (PQ_y*PR_z - PQ_z*PR_y, PQ_z*PR_x - PQ_x*PR_z, PQ_x*PR_y - PQ_y*PR_x)
= (1*3 - 1*(-1), 1*1 - 0*3, 0*(-1) - 1*1)
= (3 + 1, 1 - 0, 0 - 1)
= (4, 1, -1)
Therefore, we can state that a vector orthogonal to the plane defined by points P(1,0,0), Q(1,1,1), and R(2,-1,3) is (4, 1, -1).
To learn more about vector orthogonal visit : https://brainly.com/question/30905184
#SPJ11
7x-3y=12
Need graphing or explaining how to do it bc I am confused.
Answers
Answer:
Take two points and connect them with a line.
Step-by-step explanation:
We can take the points (0,-4) and (1,-\(\frac{5}{3}\)). Now we can connect the two points with a line and we get our graph.
Answer:
(See the third picture)
Step-by-step explanation:
Start by turning everything to slope-intercept form:
\(7x-3y=12\\-3y=-7x+12\\y=\frac{7}{3}x-4\)
Next, plot down the y-intercept on the graph (which in this case is -4):
(The y-intercept is the point where a line crosses the y-axis, thus, the y-intercept must be (0, y))
(See the first picture)
Next up, plot down the next point with the slope, recall that the graph is rise over run, or more specifically, y over x.
The slope is 7/3, the rise is 7 and the run is 3, so to draw the next point, start at your y-intercept, and go 7 units up, and 3 to the right, the next point should look like this:
(See the second picture)
And finally, draw a straight line across both points:
(See the third picture)



The continuous random variable V has a probability density function given by: 6 f(v) = for 3 ≤ ≤7,0 otherwise. 24 What is the expected value of V? Number
Answers
The expected value of the continuous random variable V is 5. The expected value of V is 5, indicating that, on average, we expect the value of V to be around 5.
To calculate the expected value of a continuous random variable V with a given probability density function (PDF), we integrate the product of V and the PDF over its entire range.
The PDF of V is defined as:
f(v) = 6/24 = 0.25 for 3 ≤ v ≤ 7, and 0 otherwise.
The expected value of V, denoted as E(V), can be calculated as:
E(V) = ∫v * f(v) dv
To find the expected value, we integrate v * f(v) over the range where the PDF is non-zero, which is 3 to 7.
E(V) = ∫v * (0.25) dv, with the limits of integration from 3 to 7.
E(V) = (0.25) * ∫v dv, with the limits of integration from 3 to 7.
E(V) = (0.25) * [(v^2) / 2] evaluated from 3 to 7.
E(V) = (0.25) * [(7^2 / 2) - (3^2 / 2)].
E(V) = (0.25) * [(49 / 2) - (9 / 2)].
E(V) = (0.25) * (40 / 2).
E(V) = (0.25) * 20.
E(V) = 5.
Therefore, the expected value of the continuous random variable V is 5.
The expected value represents the average value or mean of the random variable V. It is the weighted average of all possible values of V, with each value weighted by its corresponding probability. In this case, the expected value of V is 5, indicating that, on average, we expect the value of V to be around 5.
Learn more about random variable here
https://brainly.com/question/17217746
#SPJ11
Find the missing value.
Hint: Use the number line to find the missing value.
4= -24
{
-15
→
-10
-50
5
10
15

Answers
because 6-2=4
a) the average height of sunflowers in a field is 64 in. with a standard deviation of 3.5 in. on a piece of paper, draw a normal curve for the distribution, including the values on the horizontal axis at one, two, and three standard deviations from the mean. describe your drawing in as much detail as possible, and explain how you came up with each of your labels.
Answers
The normal distribution is a mathematical model that is often used to describe a wide range of natural phenomena, such as the height of sunflowers. It is characterized by its bell-shaped curve, which is symmetrical around the mean. In this case, the average height of sunflowers in a field is 64 in. with a standard deviation of 3.5 in.
To find these values, we can use the empirical rule, which states that approximately 68% of the values lie within one standard deviation of the mean, 95% lie within two standard deviations, and 99.7% lie within three standard deviations. Therefore, the values at one, two, and three standard deviations from the mean are:
- One standard deviation below the mean: 64 - 3.5 = 60.5 in
- One standard deviation above the mean: 64 + 3.5 = 67.5 in
- Two standard deviations below the mean: 64 - 2(3.5) = 57 in
- Two standard deviations above the mean: 64 + 2(3.5) = 71 in
- Three standard deviations below the mean: 64 - 3(3.5) = 53.5 in
- Three standard deviations above the mean: 64 + 3(3.5) = 74.5 in
To draw the normal curve, we start by drawing a horizontal axis representing the range of values for the variable, in this case, the height of sunflowers. We then label the mean value, which is 64 in, at the center of the axis. Next, we draw the curve of the distribution, which should be bell-shaped and symmetrical around the mean. The curve should be highest at the mean and taper off on either side.
To label the one, two, and three standard deviations from the mean, we can use the values we calculated above. We draw vertical lines at each of these values, which represent the distance from the mean in terms of standard deviations. We then label each line with the corresponding value, as follows:
- One standard deviation below the mean: 60.5 in
- One standard deviation above the mean: 67.5 in
- Two standard deviations below the mean: 57 in
- Two standard deviations above the mean: 71 in
- Three standard deviations below the mean: 53.5 in
- Three standard deviations above the mean: 74.5 in
Finally, we label the units on the horizontal axis, which in this case is inches. The result should be a clear and accurate visual representation of the distribution of sunflower heights in the field.
To know more about symmetrical visit :
https://brainly.com/question/31184447
#SPJ11
determine the sine and cosine of 90 degrees
Answers
Which of the following statements are true?(Choose all correct answers)Methods cannot be written with parameters.Parameter values can never be used within the method code block.Methods can be written with any number of parameters.Methods can never be written with more than four parameters.Parameter values can be used within the method code block
Answers
The true statement is, Parameter values can be used within the method code block. (option e).
In computer programming, methods are used to group a set of instructions together that can be executed repeatedly. Parameters are used to pass values to a method so that the method can perform specific actions based on the values passed. Let's discuss the given statements one by one to determine which ones are true.
Parameter values can be used within the method code block.
This statement is true. Parameter values can be used within the method code block to perform specific actions. The parameter values can be manipulated or combined with other values to produce the desired result.
In summary, methods can be written with any number of parameters, and parameter values can be used within the method code block to perform specific actions. The number of parameters needed will depend on the specific task the method is designed to perform.
Hence the option (e) is correct.
To know more about parameter here
https://brainly.com/question/30757464
#SPJ4
A counterexample proves why a statement is true
A. True
B.false
Answers
Answer:
B. False
Step-by-step explanation:
A counterexample is used to contradict or prove an argument incorrect.
a list of 2018 positive integers has a unique mode, which occurs exactly 10 times.what is the least number of distinct values that can occur in the list?
Answers
The least number of distinct values that can occur in the list is 0 which means there will be no distinct number.
Given that:-
Number of positive integers in the list = 2018
Number of times the mode is occurring = 10
We have to find the least number of distinct values that can occur in the list.
As we have to find the least number of distinct values, let us consider that rest of the numbers are occurring 9 times in the list.
Hence, we can write,
9x + 10 = 2018
9x = 2008
x = 2008/9
This is not coming out to be an integer.
We will have to find a number less than 10 and greater than 1 which is divisible by 2008.
Such numbers are 2, 4 and, 8.
Hence, we can consider that other numbers are occurring for either 2,4 or 8 number of times and hence there is no distinct value in the list.
To learn more about mode, here:-
https://brainly.com/question/28566521
#SPJ4
URGENT!!!!!
Find the value of x that makes m n.
m
(7x - 11)
(4x + 58)
n
X =

Answers
Answer:
x = 23
7x - 11 = 4x + 58
(7x - 4x) - 11 = (4x - 4x) + 58
3x - 11 = 58
3x (- 11 + 11) = 58 + 11
3x = 69
3x/3 = 69/3
x = 23
Answer:
x=23°
Step-by-step explanation:
(7x - 11)=(4x + 58)
7x-4x=58+11
3x=69
x=23
A(n) ______________________________ is formed by one side of the triangle and the extension of an adjacent side.
Answers
A triangle is a three-sided polygon that consists of three sides and three angles. An extension of a side of a triangle is a line segment that is drawn from one of the endpoints of the side that extends beyond the side.
If we extend one side of the triangle and draw a line that passes through one of the adjacent vertices, the resulting shape is called a triangle's exterior angle. This exterior angle is formed by one side of the triangle and the extension of an adjacent side.
In other words, an exterior angle of a triangle is an angle that is formed by one side of a triangle and the extension of an adjacent side of the triangle.
To know more about polygon. here
https://brainly.com/question/1592456
#SPJ4
1. What is the Greatest Common Factor of 8 and 36? (1 point)
-2
-4
-6
-8
Answers
Answer:
4 is the answer no hate if I'm wrong :)
Answer
GCF of 8 and 36 is 8
CORRECT ANSWER Is 4 SORRY FOR THE MESS UP
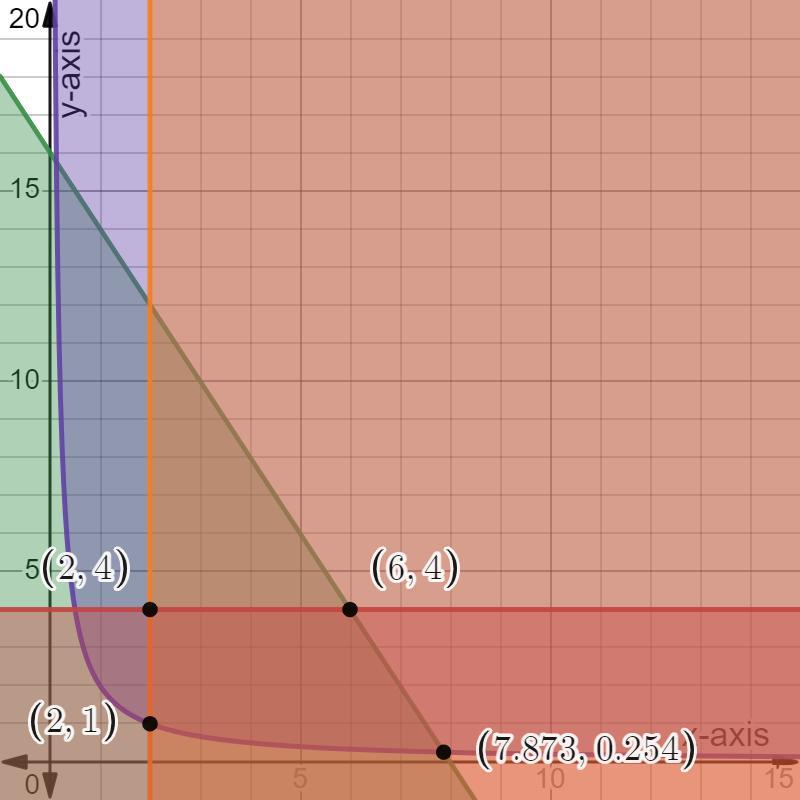
4. Solve the problem given with the constrains and objective function. Maximize profit 30X, + 40X2 Subject to; 4X₁ + 2X₂ ≤ 32
2X₁ X₂ ≥ 4 X₁ ≥ 2 X₂ ≤ 4
Answers
The maximum profit is 340, and it occurs when X₁ = 6 and X₂ = 4.
The objective is to maximize the profit function 30X₁ + 40X₂, subject to the following constraints:
4X₁ + 2X₂ ≤ 32
2X₁X₂ ≥ 4
X₁ ≥ 2
X₂ ≤ 4
Let's break down the steps to solve the problem:
Step 1: Graph the feasible region:
Plot the equations 4X₁ + 2X₂ = 32, 2X₁X₂ = 4, X₁ = 2, and X₂ = 4 on a coordinate plane.
Shade the feasible region that satisfies all the constraints.
Step 2: Identify the corner points and evaluate the profit:
1. For the point (2, 4):
Profit = 30(2) + 40(4) = 60 + 160 = 220
2. For the point (6, 4):
Profit = 30(6) + 40(4) = 180 + 160 = 340
3. For the point (7.873, 0.254):
Profit = 30(7.873) + 40(0.254) = 236.19 + 10.16 = 246.35
4. For the point (2, 1):
Profit = 30(2) + 40(1) = 60 + 40 = 100
Comparing the profits obtained at each corner point, we find that the maximum profit is achieved at the point (6, 4), which yields a profit of 340.
Therefore, the maximum profit is 340, and it occurs when X₁ = 6 and X₂ = 4.
To know more about maximum profit, refer here:
https://brainly.com/question/17200182
#SPJ4
Answer ASAP! Will mark Brainliest
Which statement is true about the function f(x)= √x?
A) The domain of the graph is all real numbers.
B) The range of the graph is all real numbers.
C) The domain of the graph is all real numbers less than or equal to 0.
D) The range of the graph is all real numbers greater than or equal to 0.
Answers
Answer: The correct answer is D the range of the graph is all real numbers greater than or equal to 0.
Step-by-step explanation
Range [0,infinity] {y|y greater than or equal to 0}
Answer:
D
Step-by-step explanation:
is y= x√5 a square root function?
Answers
Answer:
Yes, y = x√5 is a square root function.
Step-by-step explanation:
Yes, y = x√5 is a square root function.
A square root function is a function of the form y = √x where x is the independent variable and y is the dependent variable.
In this case, we can rewrite y = x√5 as y = √(x^2 * 5). Since x^2 is the independent variable, and y is the dependent variable, we can see that this is a square root function with a coefficient of √5.
So, even though the coefficient is not 1, it is still a square root function
If someone can do this whole thing for me I will give brainiest.

Answers
Answer:
A= x r^2
A= x r x r
r means radius
The value of pi() is 3.14
r^2 means radius x radius
Substitute the radius for r: A= x 7^2
Square the radius: 7 x 7= 49
Area in terms of pi(): 49
Area in terms of square inches: 153.86 in^2
Divide the diameter by 2: 12 ÷ 2= 6
Substitute the radius for r: A= x 6^2
Square the radius: 6 x 6= 36
Area in terms of pi(): 36
Area in terms of square inches: 113.04 in^2
Step-by-step explanation:
-4/5 x 2 1/2
Can someone please give me a step-by-step answer
Answers
Answer:
Hope it helps you............................

how many ways are there to choose a president, vice president, secretary, and treasurer of the club, where no person can hold more than one office?
Answers
The number of ways to chose a president, vice president, secretary, and treasurer of the club, where no person can hold more than one office is 11880.
If the person cannot hold more than one office.
Then the number of ways of selecting a president, vice president, secretary and treasurer of the club from the club consisting of 12 member is given by the permutation ¹²P₄.
Because we have to select four member out of 12,
So, solving further,
= ¹²P₄
= 12!/(12-4)!
= 12!/8!
= 12 x 11 x 10 x 9
= 11880.
So, there are a total of 11880 ways to chose the members.
To know more about permutation, visit,
https://brainly.com/question/1216161
#SPJ4
Complete question - A club has 12 members A president, a vice president, a secretary, and a treasurer are to be chosen from these members. A member cannot serve for more than one position. In how many ways can this be down?
Muriel told Shana that one of the products in the table was incorrect.
Which value in the table is incorrect?
What is the value Shana should have written?
Answers
The product of numbers or expressions involve multiplying the numbers and the expressions
The incorrect value in the table is -2yThe correct value is -2xyHow to determine the incorrect valueFrom the table, we have the following product
2x* -y = -2y
or
-y * 2x =-2y
The above equation is incorrect.
This is so because, the product of 2x and -y is -2xy, not 2y
Hence, the incorrect value in the table is -2y and the correct value is -2xy
Read more about products at:
https://brainly.com/question/10873737
Answer:
A and B
Step-by-step explanation:
the angle of a triangle in the ratio 1:3:5 how much is the larger angle
Answers
Answer:
100°
Step-by-step explanation:
The sum of all the angles in a triangle is 180°.
This is 1 + 3 + 5 = 9
180 ÷ 9 = 20
The scale factor is 20.
Multiply 5 (the greatest angle) by the scale factor.
5 x 20 = 100
Please help me outttt

Answers
Answer:
I thing the answer is 16
Step-by-step explanation: because if you do 2x2=4, then 4x4=16mm
Evaluate the expression for the given values.
12x+5y
------------
3z, where x=12, y = 6, and z = 3
Enter your answer in the box.
Answers
(12x+5y)/3z
substitute in values
(12(12) + 5(6)) / 3(3)
simplify
(144 + 30) / 9
add
174 / 9
factor out a 3
58 / 3
Hope this helps :)
If you need any more explanation, feel free to ask. If this really helps, consider marking brainliest.
- Jeron
1. Use Newton's method to approximate to six decimal places the only critical number of the function f(x) = ln(1 + x - x2 + x3). 2. Find an equation of the line passing through the point (3,5) that cuts off the least area from the first quadrant. 3. Find the function f whose graph passes through the point (137, 0) and whose derivative function is f'(x) = 12x cos(x2)
Answers
1. Using Newton's method, the only critical number of the function f(x) = ln(1 + x - x^2 + x^3) is approximately 0.789813.
2. The equation of the line passing through the point (3,5) that cuts off the least area from the first quadrant is y = -(5/3)x + 20/3.
3. The function f(x) = sin(x^2) - 137x + 231 is the function that passes through the point (137, 0) and has a derivative function of f'(x) = 12x cos(x^2).
To find the critical number of the function f(x) = ln(1 + x - x^2 + x^3), we can apply Newton's method.
The derivative of f(x) is given by f'(x) = (1 - 2x + 3x^2) / (1 + x - x^2 + x^3). By iteratively applying Newton's method with an initial guess, we can approximate the critical number. The process continues until we reach the desired level of accuracy. In this case, the critical number is approximately 0.789813.
To find the line passing through the point (3,5) that cuts off the least area from the first quadrant, we need to minimize the area of the triangle formed by the line, the x-axis, and the y-axis.
The equation of a line passing through (3,5) can be written as y = mx + c, where m represents the slope and c is the y-intercept. By minimizing the area of the triangle, we minimize the product of the base and height.
This occurs when the line is perpendicular to the x-axis, resulting in the least area. Therefore, the line equation is y = -(5/3)x + 20/3.
To find the function f(x) that passes through the point (137, 0) and has a derivative function of f'(x) = 12x cos(x^2), we integrate the derivative function with respect to x.
Integrating f'(x) gives us f(x) = sin(x^2) - 137x + C, where C is the constant of integration. To determine the value of C, we substitute the given point (137, 0) into the equation. This gives us 0 = sin(137^2) - 137(137) + C, which allows us to solve for C. The resulting function is f(x) = sin(x^2) - 137x + 231.
Learn more about Newton's method:
https://brainly.com/question/31910767
#SPJ11
Find a formula an for the nth term of the geometric sequence whose first term is a1=3 such that anan+1=1/10 for n≥1 10. Find an explicit formula for the nth term of the add one to each term.) 11. Find an explicit formula for the nth term of the sequence satisfying a1=0 and an=2an−1+1 for n≥2
Answers
To find an explicit formula for the nth term of the sequence satisfying\(\(a_1 = 0\) and \(a_n = 2a_{n-1} + 1\) for \(n \geq 2\),\) we can use recursive formula to generate the terms of the sequence.
Given:
\(\(a_1 = 0\)\\\(a_n = 2a_{n-1} + 1\) for \(n \geq 2\)\)
Using the recursive formula, we can generate the terms of the sequence as follows:
\(\(a_2 = 2a_1 + 1 = 2(0) + 1 = 1\)\\\(a_3 = 2a_2 + 1 = 2(1) + 1 = 3\)\)
\(\(a_4 = 2a_3 + 1 = 2(3) + 1 = 7\)\\\(a_5 = 2a_4 + 1 = 2(7) + 1 = 15\)\)
From the pattern, we observe that the nth term of the sequence is given by \(\(2^{n-2} - 1\).\)
Therefore, the explicit formula for the nth term of the sequence satisfying \(\(a_1 = 0\) and \(a_n = 2a_{n-1} + 1\) for \(n \geq 2\) is: \\\\\a_n = 2^{n-2} - 1.\]\)
To know more about sequence visit-
brainly.com/question/32355325
#SPJ11
Evaluate this expression: 3x + 9x -5
Answers
Answer:
12x - 5
Step-by-step explanation:
3x + 9x - 5 can be easily simplified by combining like terms.
3x and 9x are like terms because they both contain the same variable and the same exponent (understood to be 1).
Therefore, because an addition sign separates the two terms, it is expected of you to add the two together. To do this, just add the terms together as you would any other terms.
3x + 9x = 12x
Because the 5 is the only constant in the equation, it cannot be combined with anything else.
The simplified expression is 12x - 5.
The cost x of the Sennet family’s meal at a restaurant is $172.65, and they tip 20%. Write and use an equation to find the total cost y of the dinner.
Answers
Answer:
the answer would be 196.25
Step-by-step explanation:
Carl and Stephen and Brittney completed in a shot put competition .Stephen's toss was 4.08 feet farther than Brittney's. Carl's toss was 2.14 shorter then Stephen's
Answers
Answer:
R4ARAQuestion
Carl and Stephen and Brittney completed inQuestion
Carl and Stephen and Brittney completed in a shot put competition .Stephen's toss was 4.08 feet farther than Brittney's. Carl's toss was 2.14 shorter then Stephen's a shot put competition .Stephen's toss was 4.08 feet farther than Brittney's. Carl's toss was 2.14 shorter then Stephen's RARRARAGG
Step-by-step explanation:
Analyzing Speed Yohan Blake ran the 100-meter race in the 2012 Olympics in 9.75 seconds. Compare the speeds if he ran the 200-meter race in 19.5 seconds. round to the nearest hundredth.
Answers
Answer:
The two speeds are equal
Step-by-step explanation:
The speed is the distance divided by the time
100 meters / 9.75 seconds = 10.25641026 meters per second
Rounded to the nearest hundredth 10.26 meters per second
200 meters / 19.5 seconds = 10.25641026 meters per second
Rounded to the nearest hundredth 10.26 meters per second
The two speeds are equal
\(\sf{\bold{\blue{\underline{\underline{Given}}}}}\)
⠀Analyzing Speed Yohan Blake ran the 100-meter race in the 2012 Olympics in 9.75 seconds.⠀⠀⠀he ran the 200-meter race in 19.5 seconds. round to the nearest hundredth.\(\sf{\bold{\red{\underline{\underline{To\:Find}}}}}\)
Compare the speeds⠀⠀⠀⠀\(\sf{\bold{\purple{\underline{\underline{Solution}}}}}\)
⠀
we know that,
\(\boxed{\sf{speed=\dfrac{distance}{time}} }\)
In the 100-meter race in the 2012 Olympics he takes 9.75 sec
speed=100/9.75speed =10.2564...speed=10.26BUTTT,
he ran the 200-meter race in 19.5 seconds.
speed=200/19.5speed=10.2564..speed=10.26According to the question,
we have to compare the speed
100-meter race in the 2012 Olympics he takes 9.75 sec=200-meter race in 19.5 seconds.10.26=10.26the speeds are equal⠀⠀⠀
\(\sf{\bold{\green{\underline{\underline{Answer}}}}}\)
The two speeds are equal of Yohan Blake.