Ron borrowed $30,000 to start up his consulting business. The loan had a simple interest rate of 5.5% for 4 years. Use the formula I=prt to find the amount of interest he will pay on the loan. I= interest, P=principal, R=rate (expressed as a decimal 0.055), T=time in years.
Answers
we use formula of simple interest
\(I=p\times r\times t\)the replace our values
\(\begin{gathered} I=(30000)\times(0.055)\times(4) \\ I=6600 \end{gathered}\)The amount of interest he will pay $6,600
Answer:
$6,600
Step-by-step explanation:
So first of all you want to start by finding what P, r and t would be.
P = Principal amount ($$)r = interest rate (%)t = time (years)Once I found all of those I put them into the equation (l = Prt) and solved (by putting it into a calculator obviously). That is how I came up with my answer. Check the screenshot provided to see what P, r and t would be and to see all my work! :)
Hope this helps! :)
Have a great day!

Related Questions
Can u pleaseee answer all parts pleaseeeee <3333
please help meee


Answers
a. In interval notation, Increasing intervals: (12pm, 1pm) U (1pm, 2pm) U (2pm, 3pm). Decreasing intervals: (8am, 9am) U (11am, 12pm). Constant intervals: (9am, 10am) U (10am, 11am)
b. The increase in cost between 12 noon and 3 pm is $2.
c. Yellow Cab has a lower price per 1km than Swift ride at (8am, 9am) (9am, 10am) (2pm 3pm)
How do you express a data set in interval notations?Interval notation is used to represent continuous intervals of numbers or values, like ranges on a number line.
The graph shows that from 8-9am, and 11-12pm, the cost from Swift Ride decreases.
We can represent it as (8am, 9am) U (11am, 12pm).
It increases at these times (12pm, 1pm) U (1pm, 2pm) U (2pm, 3pm).
And stays constant at : (9am, 10am) U (10am, 11am)
Cost increase from 12 to 3pm,We simply deduct the 12pm's cost from 3pm's cost.
So, we have
Cost increase = $3.5 - $1.5
Evaluate the difference
Cost increase = $2
Hence, the cost increase is $2
The time interval where the cost is lowerWhen you plot the points provided for Yellow cab, you'll notice that Yellow Cab has a lower price per 1km than Swift ride at (8am, 9am) (9am, 10am) (2pm 3pm)
Find more exercises on Interval notation;
https://brainly.com/question/17249352
#SPJ1
A manufacturer of fuses claims that with 20% overload, the fuses will blow
in less than 10 minutes on the average. To test this claim, a random sample of 20 of
these fuses was subjected to a 20% overload, and the times it took them to blow had
the mean of 10.4 minutes and a sample standard deviation of 1.6 minutes. It can be
assumed that the data constitute a random sample from a normal population. Do they
tend to support or refute the manufacturer’s claim?
Answers
Using the t-distribution, it is found that since the p-value of the test is greater than the standard significance level of 0.05, the data refutes the manufacturer's claim.
What are the hypothesis tested?At the null hypothesis, we test if there is not enough evidence that the mean is less than 10 minutes, that is:
\(H_0: \mu \geq 10\)
At the alternative hypothesis, we test is there is enough evidence that the mean is less than 10 minutes, that is:
\(H_1: \mu > 10\)
What is the test statistic?The test statistic is given by:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
The parameters are:
\(\overline{x}\) is the sample mean.\(\mu\) is the value tested at the null hypothesis.s is the standard deviation of the sample.n is the sample size.The values of the parameters are given as follows:
\(\overline{x} = 10.4, \mu = 10, s = 1.6, n = 20\)
Hence the test statistic is:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
\(t = \frac{10.4 - 10}{\frac{1.6}{\sqrt{20}}}\)
t = 1.12.
What is the p-value?Using a t-distribution calculator, considering a left-tailed test, as we are testing if the mean is less than a value, with t = 1.12 and 20 - 1 = 19 df, the p-value is of 0.8617.
Since the p-value of the test is greater than the standard significance level of 0.05, the data refutes the manufacturer's claim.
More can be learned about the t-distribution at https://brainly.com/question/13873630
#SPJ1
Prove whether each argument is valid or invalid. First find the form of the argument by defining predicates and expressing the hypotheses and the conclusion using the predicates. If the argument is valid, then use the rules of inference to prove that the form is valid. If the argument is invalid, give values for the predicates you defined for a small domain that demonstrate the argument is invalid.
The domain for each problem is the set of students in a class.
(c)Every student who missed class got a detention.
Penelope is a student in the class.
Penelope got a detention.
Penelope missed class.
(e)Every student who missed class or got a detention did not get an A.
Penelope is a student in the class.
Penelope got an A.
Penelope did not get a detention.
Answers
(c) The argument is valid, and we can conclude that Penelope missed class because she got a detention.
(e) The argument is valid, and we can conclude that Penelope did not miss class because she got an A and did not get a detention.
(c) To prove this argument's validity, we need to define the predicates and express the hypotheses and conclusion using them:
Let "M(x)" be the predicate "x missed class", and "D(x)" be the predicate "x got a detention".
Hypotheses: M(Penelope), D(Penelope)
Conclusion: M(Penelope)
Using modus ponens, which states that if P implies Q and P is true, then Q must be true, we can conclude that M(Penelope) is true:
From M(Penelope) and "Every student who missed class got a detention", we have D(Penelope)
From D(Penelope), we have M(Penelope)
So, the argument is valid, and we can conclude that Penelope missed class because she got a detention.
(e) To prove this argument's validity, we need to define the predicates and express the hypotheses and conclusion using them:
Let "M(x)" be the predicate "x missed class", "D(x)" be the predicate "x got a detention", and "A(x)" be the predicate "x got an A".
Hypotheses: A(Penelope), ~D(Penelope)
Conclusion: ~M(Penelope)
Using modus tollens, which states that if P implies Q and Q is false, then P must be false,
we can conclude that M(Penelope) is false:
From A(Penelope) and "Every student who missed class or got a detention did not get an A",
we have ~M(Penelope) & ~D(Penelope)
From ~D(Penelope), we have ~M(Penelope)
So, the argument is valid, and we can conclude that Penelope did not miss class because she got an A and did not get a detention.
For more questions on: modus tollens
https://brainly.com/question/26325801
#SPJ4
Two fire-lookout stations are 13 miles apart, with station B directly east of station A.
Both stations spot a fire. The bearing of the fire from station A is N35°E and the
bearing of the fire from station B is N49°W. How far is the fire from station B?
Choose the correct formula given below.

Answers
The distance between the fire and station B is 10.7miles
What is sine rule?The sine rule states that if a, b and c are the lengths of the sides of a triangle, and A, B and C are the angles in the triangle; with A opposite a, etc., then a/sinA=b/sinB=c/sinC.
The angle at A = 90- 35
= 55°
The angle at B = 90-49
= 41°
Angle at the fire = 180-(41+55)
= 180-96 = 84°
Using sine rule
sin84/13 = sin55/x
xsin84 = 13sin55
0.995x = 10.65
x = 10.65/0.995
x = 10.7 miles
Therefore the distance between the fire and station B is 10.7 miles.
learn more about sine rule from
https://brainly.com/question/27174058
#SPJ1
Decide whether the data in the table represent a linear function or an
exponential function.
O A. The data represent a linear function because there is a common difference of -8.
OB. The data represent an exponential function because there is a common ratio of 2.
C. The data represent a linear function because there is a common
difference of 8.
D. The data represent an exponential function because there is a common ratio of 1/2

Answers
f we plot the provided points, we'd end up with something like the picture below, which is a line, mind you a declining line from left to right, so we can pretty see it has a negative slope, to get the slope we can just pick any two given points and check what it might be as well as get its equation, hmmm let's use the points of (4,-8) and (2,8)\((\stackrel{x_1}{4}~,~\stackrel{y_1}{-8})\qquad (\stackrel{x_2}{2}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{8}-\stackrel{y1}{(-8)}}}{\underset{run} {\underset{x_2}{2}-\underset{x_1}{4}}}\implies \cfrac{8+8}{-2}\implies \cfrac{16}{-2}\implies -8 \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-8)}=\stackrel{m}{-8}(x-\stackrel{x_1}{4})\implies y =-8x+24\)
so is linear because it has a slope (common difference) of -8,

write 2 equivalent ratios for each ratio below : 3/ 38\(\frac{3}{38\\}\)
Answers
Answer:14
Step-by-step explanation:
Akigr sksjb82792?/ =x so that is ansewr
An arborist is preparing the fuel mix for her chainsaw before climbing a tree to remove a dead limb. The two-stroke chainsaw
requires a 5% mix of engine oil to gas-that is, the amount of oil should be 5% of the amount of gas. How much engine oil should
be added to a jerry can that contains 3.8 gallons of gas?
(Type a whole number or a decimal)
Answers
Answer:
To determine the amount of engine oil needed, we need to find 5% of 3.8 gallons:
0.05 x 3.8 = 0.19
So, 0.19 gallons of engine oil should be added to the jerry can.
Three graphs are given below.
For each, choose its equation from the following.
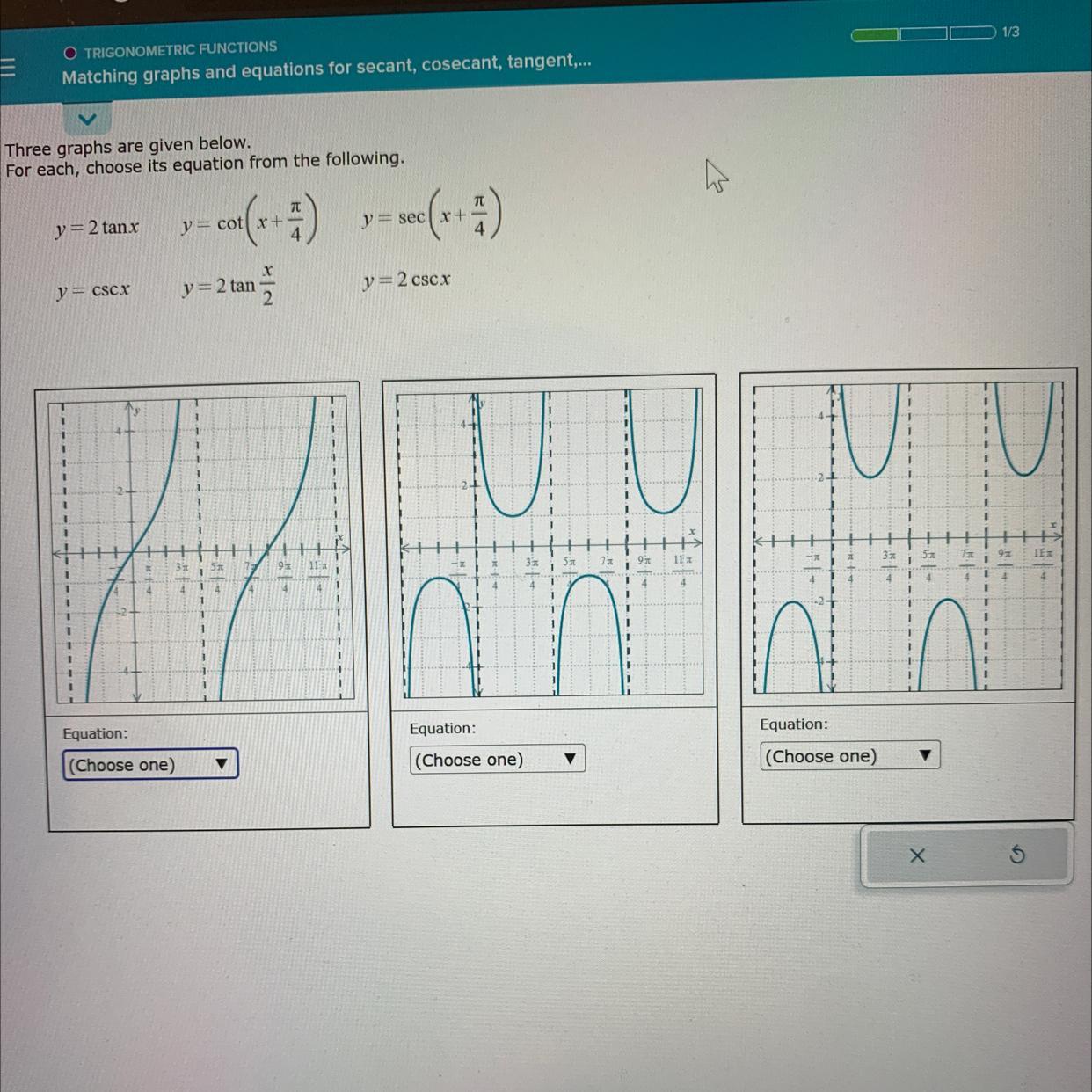
Answers
How do you solve this??
21 a(little 6) b(little 5)
————————————
7 a(little 3) b
Answers
\((21a^6b^5) / (7a^3b)\) simplifies to \(3a^3b^4.\)
To solve this problemWe can use the rules of exponents and simplify the terms with the same base.
Dividing the coefficients: 21 / 7 = 3.
For the variables, you subtract the exponents: \(a^6 / a^3 = a^(^6^-^3^) = a^3.\)
Similarly,\(b^5 / b = b^(5-1) = b^4\).
Putting it all together, the simplified expression is:
\(3a^3b^4.\)
Therefore, \((21a^6b^5) / (7a^3b)\) simplifies to \(3a^3b^4.\)
Learn more about rules of exponents here : brainly.com/question/11975096
#SPJ1
A random sample of 40 collision claims of 30 to 49 year old drivers results in a mean claim of $3669 with a standard deviation of $2029. Another random sample of 40 collision claims of 20 to 29 year old drivers results in a mean claim of $4586 with a standard deviation of $2302. Is there evidence that 20 to 29 year old drivers have a higher mean accident claim? (Let population 1 be 20-to-29 yr old drivers and population 2 be the 30 to 49 year old drivers.) Calculate the appropriate test-statistic. Round your answer to 2 decimal places.
Answers
The appropriate test statistic is approximately 1.89.
To determine if there is evidence that 20 to 29-year-old drivers have a higher mean accident claim compared to 30 to 49-year-old drivers, we can perform a two-sample t-test.
The test statistic can be calculated using the following formula:
\(t = (mean1 - mean2) / \sqrt{(s1^2 / n1) + (s2^2 / n2)}\)
where:
mean1 and mean2 are the sample means of the two populations,
s1 and s2 are the sample standard deviations of the two populations,
n1 and n2 are the sample sizes of the two populations,
Given the following information:
For population 1 (20 to 29-year-old drivers):
Sample mean (mean1) = $4586
Sample standard deviation (s1) = $2302
Sample size (n1) = 40
For population 2 (30 to 49-year-old drivers):
Sample mean (mean2) = $3669
Sample standard deviation (s2) = $2029
Sample size (n2) = 40
Calculate the test statistic (t):
\(t = (4586 - 3669) /\sqrt{ (2302^2 / 40) + (2029^2 / 40))\)
Calculating this expression:
t ≈ 917 / √(132360.1 + 102996.025)
t ≈ 917 / √(235356.125)
t ≈ 917 / 485.086
t ≈ 1.89
Therefore, the appropriate test statistic is approximately 1.89.
Learn more about test statistic click;
https://brainly.com/question/31746962
#SPJ1
1. A new compact has a sticker price of $14500. Options add another $982. Destination charges are $592. Dealer preparation is 5% of the total price. Sales tax is 7%. Tag fee is $145. Title fee is $45. What is the total price of the vehicle?
2. The selling price of a used car is $8850. Trade in allowance is $1500. Tax is 8%. Tag fee is $130. Title fee is $35. Finance charges are 9.5% annual simple interest. What is the total price of the financed amount? What are the total finance charges? What are the monthly payments if the vehicle is financed for 3 years? What is the total deferred price of the car?
3. The total deferred price of a car is $28000. After a down payment of $2100, the monthly payments are $380. How long is the financing agreement?
4. Stanley bought a new car with a sticker price of $19200. The dealer agreed to a 6% discount. The sales tax was 8% of the selling price. The tag fee was $65, and the title fee was $45. What is the total price of the car? The interest rate is 9% for financing the car for 5 years. What is the total deferred price after all the payments were made?
5. Mark bought a truck with a sticker price of $23000 plus additional options totaling $3500. He received a 4% discount and a $1500 trade-in allowance. The tax was 7%, tag fee was $125, and title fee was $75. He bought an extended warranty for $700, which was financed into the total cost of the truck. The interest rate was 6.5% for 5 years. How much are the monthly payments?
Answers
The total price of the vehicle would be $18,192.88.
The total deferred price of the car would be $11,191.60.
The length of the financing agreement is 68 months .
The total deferred price after the payments was $19,601.84.
The monthly payments would be $516.92.
How to find the price of the vehicle ?Subtotal = Base price + Options + Destination charges
Subtotal = $14,500 + $982 + $592 = $16,074
Dealer preparation = 5% of subtotal
Dealer preparation = 0.05 x $16,074 = $803.70
Sales tax = 7% of subtotal
Sales tax = 0.07 x $16,074 = $1,125.18
Total price = Subtotal + Dealer preparation + Sales tax + Tag fee + Title fee
Total price = $16,074 + $803.70 + $1,125.18 + $145 + $45 = $18,192.88
How to find the total deferred price ?Tax = 8% of selling price = 0.08 x $8,850 = $708
Tag fee = $130
Title fee = $35
Total amount financed = Amount financed + Tax + Tag fee + Title fee = $7,350 + $708 + $130 + $35 = $8,223
Annual interest rate = 9.5%
Number of years financed = 3
Total finance charges = $8,223 x 0.095 x 3 = $2,341.595
Total financed amount = $8,223 + $2,341.595 = $10,564.595
Monthly payments = Total financed amount / (Number of years financed x 12 months) = $10,564.595 / (3 x 12) = $293.4615
Total deferred price = Selling price + Total finance charges = $8,850 + $2,341.595 = $11,191.595
How to find the length of the financing agreement ?Total deferred price = $28,000
Down payment = $2,100
Total amount financed = Total deferred price - Down payment = $28,000 - $2,100 = $25,900
Monthly payments = $380
Number of months = Total amount financed / Monthly payments = $25,900 / $380 = 68.16
The financing agreement is approximately 68 months long.
How to find the deferred price after the payments ?Sticker price = $19,200
Discount = 6% of sticker price = 0.06 x $19,200 = $1,152
Selling price = Sticker price - Discount = $19,200 - $1,152 = $18,048
Sales tax = 8% of selling price = 0.08 x $18,048 = $1,443.84
Total price = Selling price + Sales tax + Tag fee + Title fee = $18,048 + $1,443.84 + $65 + $45 = $19,601.84
How to find the monthly payments ?Using the formula for monthly payments on a loan:
P = (PV x r x (1 + r)^ n) / ((1 + r) ^ n - 1)
= ($26,515.80 x 0.005265 x (1 + 0.005265) ^ 60 ) / ((1 + 0.005265) ^ 60 - 1) = $516.92
Find out more on monthly payments at https://brainly.com/question/27926261
#SPJ1
determine the maximum and minimum values of the function, at what values of x are they achieved? (without using a derivative)
\(y=\sin^3x-\sin^6x\)
Answers
The maximum and minimum values of the function is solved
Given data ,
We can find the maximum and minimum values of the function by taking the derivative of y with respect to x and setting it equal to zero.
y = (sin x)³ - (sin x)⁶
y' = 3(sin x)² cos x - 6(sin x)⁵ cos x
Setting y' equal to zero:
0 = 3(sin x)² cos x - 6(sin x)⁵ cos x
0 = 3(sin x)² cos x (1 - 2(sin x)³)
sin x = 0 or (sin x)³ = 1/2
If sin x = 0, then x = kπ for any integer k.
If (sin x)³ = 1/2, then sin x = (1/2)^(1/3) ≈ 0.866. This occurs when x = π/3 + 2kπ/3 or x = 5π/3 + 2kπ/3 for any integer k.
To determine whether these values correspond to a maximum or minimum, we can use the second derivative test.
y'' = 6(sin x)³ cos² x - 15(sin x)⁴ cos² x - 9(sin x)⁴ cos x + 6(sin x)⁵ cos x
y'' = 3(sin x)³ cos x (4(sin x)² - 5(sin x)² - 3cos x + 2)
For x = kπ, y'' = 3(0)(-3cos(kπ) + 2) = 6 or -6, depending on the parity of k. This means that these points correspond to a maximum or minimum, respectively.
For x = π/3 + 2kπ/3 or x = 5π/3 + 2kπ/3, y'' = 3(1/2)^(5/3) cos x (4(1/2)^(2/3) - 5(1/2)^(1/3) - 3cos x + 2). This expression is positive for x = π/3 + 2kπ/3 and negative for x = 5π/3 + 2kπ/3, which means that the former correspond to a minimum and the latter to a maximum.
Hence , the maximum value of the function is y = 27/64, which occurs at x = 5π/3 + 2kπ/3, and the minimum value is y = -1/64, which occurs at x = π/3 + 2kπ/3
To learn more about function rule click :
https://brainly.com/question/3760195
#SPJ1
Answer:
maximum: 0.25minimum: -2Step-by-step explanation:
You want the maximum and minimum values of the function ...
y = sin³(x) -sin⁶(x)
SolutionWhen we substitute sin³(x) = z, we have the quadratic expression ...
y = z -z² . . . . . a quadratic function
Adding and subtracting 1/4, we can put this in vertex form:
y = -(z -1/2)² +1/4
MaximumThis version of the function describes a parabola that opens downward and has a vertex at (z, y) = (1/2, 1/4). The y-value of the vertex represents the maximum value of the function.
The maximum value of y is 1/4.
MinimumThe sine function is a continuous function with a range of [-1, 1]. Then z will be a continuous function of x, with a similar range. We already know that y describes a function of z that is a parabola opening downward with a line of symmetry at z = 1/2. This means the most negative value of y will be found at z = -1 (the value of z farthest from the line of symmetry). That value of y is ...
y = (-1) -(-1)² = -1 -1 = -2
The minimum value of y is -2.
__
Additional comment
The range of y is confirmed by a graphing calculator.
<95141404393>

From a table, for an ordered pair (0,y), ywill not be what?
Answers
Answer:
um hi what do u mean :)
Step-by-step explanation:
An instrument store gives a 10% discount to all students off the original cost of an instrument. During a back to school sale an additional 15% is taken off the discounted price. Julie, a student at the local high school, purchases a flute for $306. How much did it originally cost?
Answers
The original cost of flute is $408.
How to find the percentage from the total value?Suppose the value of which a thing is expressed in percentage is "a'
Suppose the percent that considered thing is of "a" is b%
Then since percent shows per 100 (since cent means 100), thus we will first divide the whole part in 100 parts and then we multiply it with b so that we collect b items per 100 items(that is exactly what b per cent means).
Given that instrument store gives a 10% discount to all students off the original cost of an instrument.
During a back to school sale an additional 15% is taken off the discounted price.
Also Julie, a student at the local high school, purchases a flute for $306.
Therefore, we can say that 75%=$306
100%=100 x 306 / 75
=$408
Learn more about percent here:
https://brainly.com/question/11549320
#SPJ1
What is the solution to the equation?

Answers
Answer:
C- t=411
Step-by-step explanation:
there is this really cool site/app called
math
way
it helps for everything, just use it
50 pts if you answer plz plz

Answers
Answer:
Step-by-step explanation:
Table 1: Add 7 to each output too get the answer for each input. Example output 1 +7 =Output 8
Table 2: Multiply each input by 6 to get the answer for each output. Example input 4 x 6=output 24
Table 3: Add 10 to each input to get output. Example 10+10=20 output
Answer:
1) To get the answer for each input, add 7 to each output. Example: output 1 + output 7 = output 8
2) To get the answer for each output, multiply each input by 6. In this case, input 4 x 6 equals output 24.
3) To get the output, add 10 to each input. Example output: 10+10=20
Can u help in solving

Answers
The cost of the jug is $24
How to determine the costLet the cost of the mug be m
Let the cost of the jug be j
Then, we have that;
3m + 2j = $84
m + j = $36
make 'j' the subject from equation (2), we have;
j = 36 - m
Substitute the value in equation (1), we have;
3m + 2(36 - m) = 84
expand the bracket
3m + 72 - 2m = 84
collect the like terms
m = 84 - 72
m = $12
Substitute the value
j = 36 - 12
j = $24
Learn about simultaneous equations at: https://brainly.com/question/16863577
#SPJ1
A 4-yard dumpster cost $95.00 monthly how much would it cost for the year?
Answer options:
A) 190.00
B) 180.00
C) 170.00
D) 160.00
Answers
If a 4-yard dumpster cost $95.00 monthly, the total cost for the year is $1,140.
How is the total cost determined?The total cost for the year of the dumpster is the product of the multiplication of the monthly cost and 12.
Multiplication is one of the four basic mathematical operations, including addition, subtraction, and division.
In any multiplication, there must be the multiplicand (the number being multiplied), the multiplier (the number multiplying the multiplicand), and the product (or the result).
The monthly cost of the 4-yard dumpster = $95.00
1 year = 12 months
The total annual cost = $1,140 ($95 x 12)
Thus, using the multiplication operation, we can find that none of the options is correct as the total annual cost but $1,140.
Learn more about mathematical operations at https://brainly.com/question/20628271.
#SPJ1
Solve for x: 3(x+1) = -6
A.-2
B.-3
C. 1
D.7/3
Answers
Answer: x = -3
Step-by-step explanation:
3(x + 1) = -6
Divide both sides by 3: 3(x + 1) / 3 = -6 / 3
x + 1 = -2
Subtract 1 from each side: x + 1 - 1 = -2 - 1
x = -3
If csc(x) = 2, for 90° < x < 180°, then
sin(x/2)=
cos(x/2)=
tan(x/2)=
Answers
csc(x) = 2 = 1/sin(x)
Solving for sin(x), we get:
sin(x) = 1/2
Next, we can use the half-angle formulas to find the values of sin(x/2), cos(x/2), and tan(x/2):
sin(x/2) = ±√[(1 - cos(x))/2] = ±√[(1 - √(1 - sin^2(x)))/2] = ±√[(1 - √(1 - (1/2)^2))/2] = ±√[(1 - √3/2)/2] = ±√[(2 - √3)/4]
cos(x/2) = ±√[(1 + cos(x))/2] = ±√[(1 + √(1 - sin^2(x)))/2] = ±√[(1 + √(1 - (1/2)^2))/2] = ±√[(1 + √3/2)/2] = ±√[(2 + √3)/4]
tan(x/2) = sin(x/2)/cos(x/2) = [±√(2 - √3)]/[±√(2 + √3)] = (2 - √3)/(2 + √3) = (√3 - 1)/(√3 + 1)
Note that the plus or minus signs in the formulas for sin(x/2) and cos(x/2) depend on the quadrant in which x lies. Since we know that 90° < x < 180°, we can conclude that sin(x/2) and cos(x/2) are both negative. Therefore:
sin(x/2) = -√[(2 - √3)/4]
cos(x/2) = -√[(2 + √3)/4]
tan(x/2) = (√3 - 1)/(1 + √3)
You are given $893 in one, five, and ten dollar bills. There are 165 bills. There are twice as many five dollar bills as there are ones and tens combined. How many bills of each type are there?
Answers
Given:
Total number of bills of one, five and ten = 165
Total amount = $893
There are twice as many five dollar bills as there are ones and tens combined.
To find:
Number of bills of each type.
Solution:
Let number of bills of one, five and ten are x, y and z respective.
Total number of bills of is 165.
\(x+y+z=165\) ...(i)
Total amount is $893.
\(1x+5y+10z=893\) ...(ii)
There are twice as many five dollar bills as there are ones and tens combined.
\(y=2(x+z)\) ...(iii)
From equation (iii), we get
\(\dfrac{y}{2}=x+z\) ...(iv)
Putting \(x+z=\dfrac{y}{2}\) in (i), we get
\(\dfrac{y}{2}+y=165\)
\(\dfrac{3y}{2}=165\)
\(3y=330\)
\(y=110\)
Putting y=110 in (iv), we get
\(x+z=\dfrac{165}{2}\)
\(x+z=55\)
\(x=55-z\) ...(v)
Putting y=110 and x=55-z in (ii), we get
\((55-z)+5(110)+10z=893\)
\(55-z+550+10z=893\)
\(9z+605=893\)
\(9z=893-605\)
\(9z=288\)
Divide both sides by 9.
\(z=32\)
Putting z=32 in (v), we get
\(x=55-32\)
\(x=23\)
Therefore, the number of one, five and ten bills are 23, 110 and 32 respectively.
There are 23 bills of $1 type.
There are 110 bills of $5 type.
There are 32 bills of $10 type.
According to the given situation
You are given $893 in one, five, and ten dollar bills.
Let the number of $1 bills be "x"
Let the number of $5 bills be "y"
Let the number of $10 bills be "z"
Total number of bills = x + y + z
Also it is given that there are twice as many five dollar bills as there are ones and tens combined
hence we can write the equations in the form of 3 variables
\(\rm x + y + z = 165........(1) \\x +5y + 10z = 893.........(2) \\y = 2\times (x+z) ..........(3) \\\)
These are three linear equations with 3 variables that can be solved for x, y and z .
On solving equations (1) , (2), and (3) we get
\(x = 23 \\y = 110 \\z = 32 \\\)
So we can conclude that there are 23 bills of $1 type.
There are 110 bills of $5 type.
There are 32 bills of $10 type.
For more information please refer to the link given below
https://brainly.com/question/21835898
Robert wants to get serious about saving for a new car. What account would you recommend
Answers
Answer:I would recommend a saving account .
Step-by-step explanation: Put a certain amount of money in evrey couple weeks or so and do not take any out
Which one of the following is a term in the following expression?
a²b³c⁴-abc+a+b-d+e
the choices are in the picture

Answers
Answer:
it's blocked for me, I'm susing my school computer
Step-by-step explanation:
The Sausage Hut is looking at a new sausage system with an installed cost of $330,000. This cost will be depreciated straight-line to zero over the project's three-year life, at the end of which the sausage system is estimated to have zero value. The project has no impact on net working capital. Each year during its three year life, the new system will increase the firm’s Sales by $455,000 and its Operating Cash Flow by $123,300.
If the tax rate is 30 percent and the discount rate is 9 percent, what is the NPV of this project?
Group of answer choices
-111,524
- $17,891
$19,405
$35,389
$1,136,217
Answers
Based on the net cashflow over the three year life, the NPV that Sausage Hut will realize is -$17,891.
What is the Net Present Value?First find the present value of the increased cashflows. As it is a constant amount of $123,300, we can treat it as an annuity.
Present value = Amount x (Present value of annuity interest factor, 9%, 3 years)
= 123,300 x 2.5313
= $312,109.29
The net present value is:
= Present value of cashflows - Amount invested
= 312,109.29 - 330,000
= -$17,890.71
= -$17,891.
In conclusion, option B is correct.
Find out more on Net Present Value at https://brainly.com/question/13228231.
could someone help me with this and show work?




Answers
The volume of the shape is 490cm³
What is volume of prisms?A prism is a solid shape that is bound on all its sides by plane faces. prism is named after the shape of these bases.
The base of this prism is rectangular. The volume of a prism is expressed as;
V = base area × height
base area = 7 × 10 = 70cm²
height = 7cm
the volume of the shape = 70× 7 = 490cm²
therefore the volume of the shape is 490cm³.
learn more about volume of prisms from
https://brainly.com/question/23766958
#SPJ1
The two-way table represents data from a survey asking schoolchildren whether they are attending a summer camp, taking swimming lessons, or both.
A 4-column table with 3 rows. The first column has no label with entries swimming lessons, no swimming lessons, total. The second column is labeled camp with entries 42, 18, 60. The third column is labeled no camp with entries 32, 4, 36. The fourth column is labeled total with entries 74, 22, 96.
Which is the joint relative frequency for school children who plan to attend camp and have swimming lessons? Round the answer to the nearest percent.
4%
19%
33%
44%
Answers
The joint relative frequency for school children who plan to attend camp and have swimming lesson is 44%.
The correct option to the given question is option d.
We are required to find the joint relative frequency for school children who plan to attend camp and have swimming lessons, rounded to the nearest percent.
To find the joint relative frequency, we use the formula as follows:
Joint relative frequency = frequency of interest / total frequency
Joint relative frequency for school children who plan to attend camp and have swimming lessons = 42 / 96
(As we are looking for the students who plan to attend camp and have swimming lessons, we are interested in the first column of the table and the entry at the intersection of the first row and second column.)
Joint relative frequency for school children who plan to attend camp and have swimming lessons = 0.4375
Joint relative frequency for school children who plan to attend camp and have swimming lessons (rounded to the nearest percent) = 44%(option d).
For more such questions on relative frequency visit:
https://brainly.com/question/3857836
#SPJ8
graph h(x)=(x-1)^2-9
Answers
The graph of h(x) = (x-1)^2 - 9 is a U-shaped parabola that opens upwards, with the vertex at (1, -9), and it extends indefinitely in both directions.
The function h(x) = (x-1)^2 - 9 represents a quadratic equation. Let's analyze the different components of the equation to understand the behavior of the graph.
The term (x-1)^2 represents a quadratic term. It indicates that the graph will have a parabolic shape. The coefficient in front of the quadratic term (1) implies that the parabola opens upwards.
The constant term -9 shifts the graph downward by 9 units. This means the vertex of the parabola will be at the point (1, -9).
Based on this information, we can draw the following conclusions:
The graph will be a U-shaped curve with the vertex at (1, -9).
The vertex represents the minimum point of the parabola since it opens upward.
The parabola will be symmetric with respect to the vertical line x = 1 since the coefficient of the quadratic term is positive.
The graph will extend indefinitely in both directions.
To accurately plot the graph, you can choose several x-values, substitute them into the equation to find the corresponding y-values, and then plot the points on the graph. Alternatively, you can use graphing software or calculators that can plot the graph of the equation for you.
Remember to label the axes and indicate the vertex at (1, -9) to provide a complete representation of the graph of h(x) = (x-1)^2 - 9.
for such more question on parabola
https://brainly.com/question/9201543
#SPJ8
graph -9x + 5y = 45

Answers
Y = mx + b
-9/5x + y = 9
y = 1.8x + 9
Find two points and graph
(0, 9), (-5,0)
Answer:
Step-by-step explanation:
The interquartile range of this data set

Answers
Answer:
IQR = Q3-Q1
=30-10
=20
Interquartile range = Quartile3-Q1
= 30 - 10
= 20
Hellpppppppppppppppppppppp

Answers
Answer:
1. MIGHT be 16 1/2
Step-by-step explanation:
causse 2/3 / 4/9 = 1 1/2
1 1/2 + 10= 11 +5 = 16
16+1/2 = 16 1/2
Answer:
9. \(16\frac{1}{9}\)
Step-by-step explanation:
1. For number 9, start by making \(10\frac{2}{3}\) into a fraction, which would be \(\frac{32}{3}\). Then, find a common denominator. Multiply both sides by 3 to get a common denominator. You should get \(\frac{96}{9}\).
2. Add \(\frac{96}{9}+\frac{4}{9}\) to get \(\frac{100}{9}\).
3. Add 5:
\(5=\frac{45}{9}\) so our equation is \(\frac{100}{9}+ \frac{45}{9}\), which is \(\frac{145}{9}\).
4. Simplify: \(16\frac{1}{9}\)
----------------------------------------------------------------------------------------------------------------
5. For number 11, start by translating the mixed numbers into fractions:
\(\frac{9}{2} +\frac{22}{3} * \frac{8}{5}\)
6. Use PEMDAS to solve:
Multiply- \(\frac{22}{3} *\frac{8}{5} = \frac{176}{15}\)
Add- \(\frac{176}{15} +\frac{9}{2}\)