Round 224.91 to the nearest whole number. Do not write extra zeros.
Answers
Answer = 225
To round a number to the nearest whole number we have to look at the digits that are after the decimal point.
If the first digit after the decimal point is greater than 5, we have to add 1 to the whole number,
In this case:
224.91
Digit after the decimal point= 9
9>5
so:
224+1 =225
Answer:
225
Step-by-step explanation:
9 is 5 or greater, meaning we round up. Therefore, 225 is the answer.
Related Questions
Solve the equation
2√x+1=7-x
Answers
x = 8 − 2√7
Explanation: Isolate the radical, then raise each side of the equation to the power of its index.
There are seven rows of nine people how many people are there in
Answers
Exercise 10
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. What is the probability of the compound event? Write your answer as a fraction or percent rounded to the nearest tenth.

Answers
The probability of choosing a 5 and then a 6 is 1/49
Finding the probability of the compound eventFrom the question, we have the following parameters that can be used in our computation:
The tiles
Where we have
Total = 7
The probability of choosing a 5 and then a 6 is
P = P(5) * P(6)
So, we have
P = 1/7 * 1/7
Evaluate
P = 1/49
Hence, the probability of choosing a 5 and then a 6 is 1/49
Read more about probability at
https://brainly.com/question/31649379
#SPJ1
Question
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. Find the probability of the compound event. Write your answer as a fraction or percent rounded to the nearest tenth. The probability of choosing a 5 and then a 6
What is the method of finding x in this problem?

Answers
Answer:
these are supplementary angles
value of X=14
Step-by-step explanation:
since they are supplementary you can set them equal to 180
13x-2=180
13x=182
x=14
Generate a plan and describe the steps needed to solve the equation. 34 = â€""(m 3)
Answers
\(m=-37\) is the solution of \(34=-(m+3)\)
Solving equations involves finding the value of the unknown variables in a given equation. The condition that both expressions match is satisfied by the value of the variable. Solving a linear equation in one variable leads to a unique solution, and solving a linear equation involving two variables gives two results. Solving a quadratic equation gives two roots. Many methods and procedures are used in solving the equation.
Now according to the question which is given to us
\(34=-(m+3)\)
First, open the brackets and then shift the numerical part to one side and the unknown part to the other side:
\(34=-m-3\\37=-m\\\)
Hence \(m=-37\)
Learn more about solving the equations here:
https://brainly.com/question/19297665
#SPJ4
Rounding decimals 3.5691 thousandths
Answers
Explanation:
There's a 9 in the thousandths place. The next digit to the right is 1, which is not 5 or more. So we'll just drop that 1 and that's why the answer is 3.569
Answer:
3.569
Step-by-step explanation:
Rounding is the process of shortening a number to a certain number of digits by finding the closest number with the desired number of digits. When rounding, look one digit to the right of the desired decimal place. In this case, you want the thousandths place. The thousandths place is 3 digits after the decimal, so look at the number next to the 9, the 1. If the number is 5 or greater round up, if it is 4 or less round down. Therefore, 3.5691 should be rounded down to 3.569.
Other examples include,
4.8736 being rounded up to 4.874
6.3168 being rounded up to 6.317
9.7340 being rounded down to 9.734
if 14 workers can paint a city wall in 4 hours, how many workers are required to do this in 2 hours?
Answers
Answer:
28
Step-by-step explanation:
Cuz there are twice as many workers so it will take twice as less time
M
18
The midpoint of segment MN is.
: 56
:: 27
:: 18
:: 9

Answers
Answer:
27
Step-by-step explanation:
...
Find all values of x in the interval [0, 2] that satisfy the equation. (enter your answers as a comma-separated list.) 5 sin(2x) = 5 cos(x)
Answers
All values of x in the interval [0, 2] that satisfy the equation are \(\frac{\pi }{2} ,3\frac{\pi }{2}\).
What is an equation?A mathematical equation is a formula that uses the equals symbol (=) to connect two expressions and express their equality. A well-formed formula consisting of two expressions linked by an equals sign is considered to be an equation in English, but the word's cognates in other languages may have slightly different definitions. For instance, an équation is defined as having one or more variables in French.
The first step in resolving a variable equation is to identify the values of the variables that lead to the equality being true. The variables that must be changed in order to solve the equation are referred to as the unknowns, and the values of the unknowns that satisfy the equality are referred to as the equation's solutions.
Calculations:
16cos(x +8sin(2x)=0
Divide by 8
2cos(x)+sin(2x)=0
Identity:
sin(2x)=2sin(x)cos(x)
2cos(x)+2sin(x)cos(x)=0
Factor:
2cos(x)(1+sin(x))=0
2cos(x)=0
cos(x)=0=x=\(\frac{\pi }{2}\),3\(\frac{\pi }{2}\)
(1+sin(x))=0
sin(x)=−1=x=3\(\frac{\pi }{2}\)
To learn more about equation , visit:
https://brainly.com/question/10413253
#SPJ4
solve for n if n/12 = 300
Answers
Answer: n=3600
Step-by-step explanation:brainliest
Answer:
25
Step-by-step explanation:
n is being divided by 12 so we divide by both sides
n/12 = 300
12/12 300/12
= 0 = 25
PLEASE HELP!!! Finish the congruence statement AND THE REASON(like SAS OR ASA OR SSS OR AAS!!
WILL GIVE BRAIN!!

Answers
The price of a CD increased from $20 to $24. Find the percent of increase
Answers
Explanation:
4/24*100%
In a study involving car owners one questions asked the owner for the number of miles driven last year. a second questions asked the owner for the age of the vehicle. a joint frequency distribution would be useful for determining whether newer cars tend to be driven more miles than older cars (True or false)
Answers
The given statement "A joint frequency distribution would be useful for determining whether newer cars tend to be driven more miles than older cars." is true because it shows the frequencies, or counts in table.
A joint frequency distribution is a table that shows the frequencies, or counts, of two or more variables for a given dataset. In this case, the two variables are the number of miles driven last year and the age of the vehicle for a sample of car owners.
A joint frequency distribution would be useful for examining the relationship between these variables and determining whether newer cars tend to be driven more miles than older cars.
By examining the joint frequency distribution, one can calculate and compare the average miles driven for different age categories of cars. For example, the average miles driven per year for cars less than 5 years old can be compared to the average miles driven per year for cars 5 to 10 years old and cars over 10 years old.
This can provide insight into whether there is a relationship between car age and miles driven, and whether this relationship is significant.
Therefore, the statement that a joint frequency distribution would be useful for determining whether newer cars tend to be driven more miles than older cars is true. It is a useful tool for examining the relationship between two variables and identifying patterns and trends in the data.
To learn more about joint frequency click on,
https://brainly.com/question/31189964
#SPJ4
Riley and Rhoda plan to buy several bags of dog food and a dog collar. each bag of food cost $7, and the dog collar cost $5.
Answers
Answer:
matters on amount of dog food bought
Step-by-step explanation:
12 for 1 bag
19 for 2 bags
26 for 3 bags
33 for 4 bags
the activity of a radioactive isotope is found to decrease by 40% in one week. what are the values of its: a) decay constant, b) half-life, c) mean lifetime?
Answers
Answer: A) The decay constant (λ) is a measure of the rate at which a radioactive isotope decays. It is defined as the probability per unit time that an atom of the isotope will decay. The decay constant can be calculated using the formula:
λ = -ln(1 - x) / t
Where x is the fraction of the original activity that has decayed (in this case, 0.40), and t is the time over which the decay occurred (in this case, one week).
B) The half-life (T1/2) is the amount of time it takes for half of the original activity of a radioactive isotope to decay. It can be calculated using the formula:
T1/2 = ln(2) / λ
C) The mean lifetime (τ) is the average amount of time an atom of a radioactive isotope will survive before it decays. It can be calculated using the formula:
τ = 1 / λ
It's important to note that the above formulas are based on the exponential decay model, which assumes that the decay process is random and that the decay constant is constant over time. If the isotope does not decay in this way, these formulas may not give accurate results.
Step-by-step explanation:
I Need Help With This Question

Answers
Answer:
Step-by-step explanation:
Dont do it. Just take the detention
Let A be the set of integers that are multiples of 3 between 1 and 15 inclusive and B be the set of even natural numbers up to and including 20. Find A∩B
Answers
After comparing the two sets, we find that 6 and 12 are the common elements of A and B. Therefore, the intersection of A and B is {6, 12}.
The set A is the set of multiples of 3 between 1 and 15 inclusive which are 3, 6, 9, 12, and 15. The set B is the set of even natural numbers up to and including 20. The set B is {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}.To find A ∩ B, we must determine the elements that A and B have in common. The common elements of A and B are 6 and 12. Thus, the intersection of A and B, A ∩ B, is {6, 12}. To find the intersection of sets A and B, we look for the common elements in the two sets. The set A is the set of multiples of 3 between 1 and 15, while the set B is the set of even natural numbers up to and including 20.
Therefore, we have A = {3, 6, 9, 12, 15} and B = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}. The intersection of the two sets A and B is the set of elements they share in common. Therefore, we have to look for elements that appear in both sets. After comparing the two sets, we find that 6 and 12 are the common elements of A and B. Therefore, the intersection of A and B is {6, 12}.
To know more about intersection visit:-
https://brainly.com/question/12089275
#SPJ11
Find the Surface area of the trapezoid
please help
show work

Answers
Answer:
259.5
Step-by-step explanation:
8.1*12=97.2
Area of trapiezium = 1/2(b+a)h
(2.8+8.1)=10.9
10.9*3/2=16.35
16.35*2=32.7
2.8*12=33.6
33.6+32.7+97.2=163.5
4*12*2=96
163.5+96=259.5
Madelyn buys 3 bottles of orange juice at the corner store for a total cost of $2.31. If each bottle costs the same amount, how much is each bottle of juice?
Answers
Answer:
cost of each bottle of juice is $0.77
Step-by-step explanation:
Let the cost of 1 bottle be $x
multiplying both side by 3
then cost of 3 bottle will be 3*$x = $3x
given that
total cost of 3 bottles = $2.31
thus
3x = 2.31
dividing both side by 3
x = 2.31/3 = 0.77
Thus, cost of each bottle of juice is $0.77
Answer:
$0.77 for each bottle of juice
Step-by-step explanation:
Madelyn buys 3 bottles of orange juice at the corner store for a total cost of $2.31.
So,
2.31/3 = 0.77
Thus, $0.77 for each bottle of juice
-TheUnknownScientist
2.
Three types of coffee beans, A, B and C, are blended in the ratio 3: 5:7 to make a bag of coffee powder.
Given that the bag contains 45 kg of coffee powder, find the mass of each type of coffee beans in the
mixture.
(ii) If A costs $7 per kg. B costs $10 per kg and C costs $13 per kg, find the cost per kg of the mixture.
Answers
Answer: The mass of each coffee bean is
A- 9 kg
B - 15 kg
C - 21 kg
The cost per kg of the mixture is 10.8$
Step-by-step explanation:
The ratio given for the three types of coffee beans is 3:5:7 so we have 3x, 5x, and 7x respectively.
3x + 5x + 7x = 45 kg
15x = 45
x = 3
Therefore as we got the value of x we can multiply with their suitable ratios
3 X 3 = 9 kg (A)
5 X 3 = 15kg (B)
7 X 3 = 21kg (C)
For the second part,
As A costs 7$ per kg and we have 9 of it multiplied and we get 63 $
Similarly, performing for B and C we get 150$ and 273$ respectively.
As we got these prices for a total of 45 kg but we need the price per kg to divide the total sum by 45 and we get 10.8 $.
For more understanding use these links
https://brainly.com/question/3796978
Answer:
total ratio is 3+5+7 = 15
bag A = 3/15 * 45 = 9 kg
bag B = 5/15 * 45 = 15 kg
bag C = 7/15 * 45 = 21 kg
ii) bag A = $7 per kg
= 7*9 = $63
bag B = $10 per kg
= 10*15 = $150
bag C = $13 per kg
= 13*21 = $273
bag A+B+C = 63+150+273 = $486
therefore $486 for 45kg
cost per kg= 486/45 = $10.8
What is the shape of the distribution for the following set of data?
X f
5 5
4 3
3 1
2 3
1 5
A)Symmetrical
B)Positively skewed
C)Negatively skewed
D)Normal
Answers
The shape of the distribution for the following set of data {X f 5 4 3 2 1 5 3 1 5} is B) Positively skewed.
What is a positively skewed distribution?A positively skewed distribution is a distribution in which the majority of the data falls on the lower side of the scale, with the tail extending to the right side of the scale.
Positive skewness is present in a distribution when the mean is higher than the median.
As a result, the mean is skewed to the right, causing the tail on the right side of the distribution.
As a result, the tail is often referred to as the "positive" tail.
Learn more about skewed distribution at
https://brainly.com/question/1604092
#SPJ11
Un ciclista tarda 3horas y 25 minutos en recorrer 150km ¿cuantos minutos tardará en recorrer 238km si lleva una velocidad constante?
Answers
Answer :
The time it will take to travel a distance of 225km is t = 9 h
What is MRU?
MRU are the acronyms that define the uniform rectilinear movement which is the movement that maintains a variation of the distance with respect to time always constant since the acceleration is null.
We will calculate the speed you have in cyclist with the initial data of traveling a distance of 125km in a time of 5 hours:
Speed = distance / time
Speed = 125km/5h
Speed = 25 km/h
We now determine a time for a 225km course
25 km/h = 225km/t
t = 225km / 25km/h
t = 9 h
Please
Solve the problem
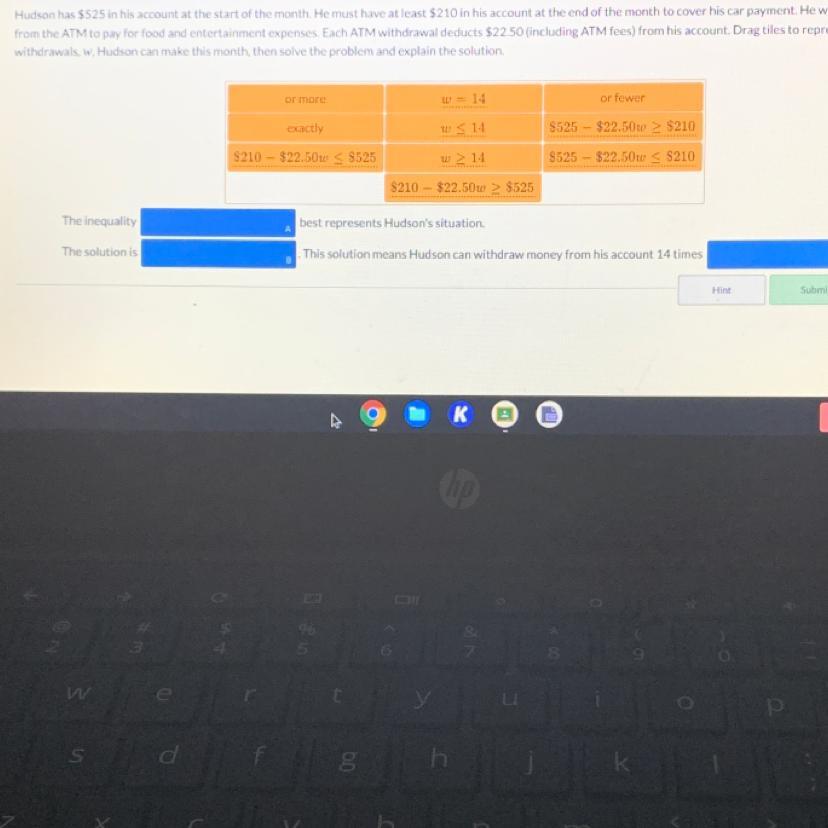
Answers
Answer:
how do you solve it the problem
jackie wants to learn more about local college. which of the following is a statistical question jackie could ask?
A. does the collage have art classes
B. what is the address of the college
C. how old are the student's
D. does the collage have a women's soccer team
Answers
to ________ a variable means to decrease its value.
Answers
Answer:
Decrement
Step-by-step explanation:
Can you find the number of triangles in the given figure?

Answers
Answer:
20?
Step-by-step explanation:
A gear in a machine has a diameter of 5 feet. Find the angle
through which the radius of the gear rotates if a point moves 20
inches around the edge of the gear.
Answers
The angle through which the radius of the gear rotates is 120/π degrees, which is approximately 38.19 degrees.
The angle through which the radius of the gear rotates can be determined using the arc length formula.
First, we need to convert the 20 inches to feet, as the diameter of the gear is given in feet. Since there are 12 inches in a foot, 20 inches is equal to 20/12 = 5/3 feet.
The circumference of a circle is given by the formula C = 2πr, where r is the radius of the circle. In this case, the radius of the gear is 5/2 = 2.5 feet. Therefore, the circumference of the gear is C = 2π(2.5) = 5π feet.
To find the angle through which the radius of the gear rotates, we can use the formula for the ratio of arc length to circumference. The ratio of the arc length (20 inches) to the circumference (5π feet) is given by:
(20/12) / (5π) = (5/3) / (5π) = 1 / (3π)
Since there are 360 degrees in a full circle, we can find the angle by multiplying the ratio by 360:
(1 / (3π)) * 360 = 120/π degrees.
Therefore, the angle through which the radius of the gear rotates is 120/π degrees, which is approximately 38.19 degrees.
Learn more about angle here:
brainly.com/question/28451077
#SPJ11
The angle through which the radius of the gear rotates is 120/π degrees, which is approximately 38.19 degrees.
The angle through which the radius of the gear rotates can be determined using the arc length formula.
First, we need to convert the 20 inches to feet, as the diameter of the gear is given in feet. Since there are 12 inches in a foot, 20 inches is equal to 20/12 = 5/3 feet.
The circumference of a circle is given by the formula C = 2πr, where r is the radius of the circle. In this case, the radius of the gear is 5/2 = 2.5 feet. Therefore, the circumference of the gear is C = 2π(2.5) = 5π feet.
To find the angle through which the radius of the gear rotates, we can use the formula for the ratio of arc length to circumference. The ratio of the arc length (20 inches) to the circumference (5π feet) is given by:
(20/12) / (5π) = (5/3) / (5π) = 1 / (3π)
Since there are 360 degrees in a full circle, we can find the angle by multiplying the ratio by 360:
(1 / (3π)) * 360 = 120/π degrees.
Therefore, the angle through which the radius of the gear rotates is 120/π degrees, which is approximately 38.19 degrees.
Learn more about angle here:
brainly.com/question/28451077
#SPJ11
If I1 ⊇ I2 ⊇ .... In ⊇... is a nested sequence of intervals and if In = [an; bn], show that a1 ≤ a2 ≤ ....... ≤ an ≤ ........ and b1 ≤ b2 ≤..... bn ≤ ......
Answers
The intervals are nested, each subsequent interval is contained within the previous one. Mathematically, this means I₁ ⊇ I₂ ⊇ ... In ⊇ ... . Therefore, we have:
1. I₁ ⊇ I₂ implies [a₁; b₁] ⊇ [a₂; b₂], which means a₁ ≤ a₂ and b₁ ≥ b₂.
2. I₂ ⊇ I₃ implies [a₂; b₂] ⊇ [a₃; b₃], which means a₂ ≤ a₃ and b₂ ≥ b₃.
To show that a1 ≤ a2 ≤ ... ≤ an ≤ ..., we need to use the fact that the sequence of intervals is nested, meaning that each interval is contained within the next one.
First, we know that I1 contains I2, so every point in I2 is also in I1. That means that a1 ≤ a2 and b1 ≥ b2.
Now consider I2 and I3. Again, every point in I3 is also in I2, so a2 ≤ a3 and b2 ≥ b3.
We can continue this process for all the intervals in the sequence, until we reach In. So we have:
a1 ≤ a2 ≤ ... ≤ an-1 ≤ an
and
b1 ≥ b2 ≥ ... ≥ bn-1 ≥ bn
This shows that the endpoints of the intervals are ordered in the same way.
Given that I₁ ⊇ I₂ ⊇ ... In ⊇ ... is a nested sequence of intervals and In = [an; bn], we can show that a₁ ≤ a₂ ≤ ... ≤ an ≤ ... and b₁ ≥ b₂ ≥ ... ≥ bn ≥ ... as follows:
Since the intervals are nested, each subsequent interval is contained within the previous one. Mathematically, this means I₁ ⊇ I₂ ⊇ ... In ⊇ ... . Therefore, we have:
1. I₁ ⊇ I₂ implies [a₁; b₁] ⊇ [a₂; b₂], which means a₁ ≤ a₂ and b₁ ≥ b₂.
2. I₂ ⊇ I₃ implies [a₂; b₂] ⊇ [a₃; b₃], which means a₂ ≤ a₃ and b₂ ≥ b₃.
Continuing this pattern for all intervals in the sequence, we can conclude that a₁ ≤ a₂ ≤ ... ≤ an ≤ ... and b₁ ≥ b₂ ≥ ... ≥ bn ≥ ... .
Visit here to learn more about sequence : https://brainly.com/question/30262438
#SPJ11
branlet will be marked so help out all my gemstones

Answers
Answer:
B is the right answer.
Step-by-step explanation:
56 + 0.08x = 164
0.08x = 164 - 56
0.08x = 108
0.08x/0.08 = 108/0.08
x = 1,350
To confirm that:
56 + 0.08x
56 + 0.08(1,350)
56 + 108
= 164
164 is the answer.
And your starting fee for five lines is $56, you would start with $56
What I would do is take $164 - $56 to get $108, then proceed to divide that by 0.08 to get 1350, and that would be my x variable
And the equation would be $56 + 0.08x =$164
Meaning the Answer Would Be:
B. 56 + 0.08x = 164, x = 1350
the lengths, in minutes, of the movies currently showing at a motive theater are shown in the data set. create a histogram that represents the data. drag the top of each bar to correct height

Answers
Based on the information given, the histogram is attached
How to explain the histogramA histogram is a graphical representation of data points organized into user-specified ranges. Similar in appearance to a bar graph, the histogram condenses a data series into an easily interpreted visual by taking many data points and grouping them into logical ranges or bins.
From the information, the range of the dataset will be:
= 68 - 32
= 36
The number of classes will be:
= 36 / 10
= 3.6
= 4 approximately.
Learn more about histogram on
https://brainly.com/question/2962546
#SPJ1
