Answers
Answer:
a) 5000
b) 123000
c) 57000
Related Questions
Find the measure of each angle in the figure below.

Answers
Answer:
a=90
b=45
c=45
d=90
e=45
f=45
Please hurry I will mark you brainliest
View the following image and create a story that MATCHES the graph. Create your own scales and values to incorporate in the story.

Answers
Step-by-step explanation:
A body at rest accelerates to 2.5 meters in 1 second, it then maintains a constant speed for 2 seconds and accelerate 2.5 meters in 2 seconds. It then maintains a constant speed for 2 seconds and finally decelerates for the next eight seconds.
scale = 1cm : 1 unit.
distance axis : 1 to 7.5 meters
Time axis : 1 to 15 seconds
When x= 12, y= 144. (a) Express y in terms of x. (b) Find the value of y when x= 7.
Answers
Answer:
see explanation
Step-by-step explanation:
Given x = 12, y = 144
We can see that y is 12 times the value of x, thus
(a)
y = 12x
(b)
when x = 7, then
y = 12 × 7 = 84
50 points!!!
7. Write and solve an inequality for the value of x.

Answers
The value of x must be between -18 and -6. The solution has been obtained using Triangle inequality theorem.
What is Triangle inequality theorem?
The triangle inequality theorem explains how a triangle's three sides interact with one another. This theorem states that the sum of the lengths of any triangle's two sides is always greater than the length of the triangle's third side. In other words, the shortest distance between any two different points is always a straight line, according to this theorem.
We are given three sides of a triangle as 8, 6 and x+20
Using Triangle inequality theorem,
⇒8+6 > x+20
⇒14 > x+20
⇒-6 > x
Also,
⇒x+20+6 > 8
⇒x+26 > 8
⇒x > -18
Also,
⇒x+20+8 > 6
⇒x+28 > 6
⇒x > -22
From the above explanation it can be concluded that x is less than -6 but greater than -22 and -18.
This means that x must lie between -18 and -6.
Hence, the value of x must be between -18 and -6.
Learn more about Triangle inequality theorem from the given link
https://brainly.com/question/1163433
#SPJ1
Find sin s, sin r , cos s , and cos r

Answers
Hi there! For this question, you need to know the ratio of sine and cosine.
sinA = opposite/hypotenusecosA = adjacent/hypotenuseDefine A = angle
opposite and adjacent side changes only if we focus on another angle.
From the picture, if we focus on angle S, the opposite would be 36. But if we focus on angle R (flip to make RT as base), see that the opposite would be 14.
Answer
sinS = 36/42 = 6/7sinR = 14/42 = 1/3cosS = 14/42 = 1/3cosR = 36/42 = 6/7The bold one is simplest form while the non-bold is non-simplest.
Questions can be asked through comment.
Hope this helps, and Happy Learning ! :)
(-9) to the 2nd power
Answers
(-9)(-9) is 81
Multiplying two negatives gives a positive
Answer:
(-9) to the 2nd power would be 81
Step-by-step explanation:
Brainliest please
What two numbers multiply to 45 and add up to 14
Answers
Answer:
5 x 9 = 45 and 5+9= 14
Step-by-step explanation:
brainliest please
Which of the following statements regarding the expansion of (x+y)^n are
correct?
O A. The coefficients of x^n and y^n both equal 1.
B. The coefficients of x^n-1 and y^n-1 both equal 1.
- 1
O c. The coefficients of x^a y^b and x^b y^a are equal.
O D. For any term x^a y^b in the expansion, a-b = n.
Answers
Answer:
A, B, and D are all true
Step-by-step explanation:
N/A
The two true statements for the expansion are A and C.
Which statements are true?In the expansion of (x + y)ⁿ, each one of the terms will have a total exponent equal to n, this means that we will have terms like:
\(x^k*y^j\)
Such that k + j = n.
Particularly, we get the terms xⁿ and yⁿ only once, so the first statement is correct, the coefficients of these terms will be 1.
It is also true that the coefficients of:
\(x^k*y^j = x^k*y^k\)
Are equal.
Then the two true statements are A and C.
If you want to learn more about expansions:
https://brainly.com/question/13602562
#SPJ2
Steel sheet length 2400 mm, wide 1200 mm, how many number of pieces 300 mm×200 mm for cutting.
6 12 24 48
Answers
The correct answer is 48 pieces.
To determine the number of pieces that can be cut from the steel sheet, we need to divide the dimensions of the steel sheet by the dimensions of each piece to see how many can fit.
Calculate the number of pieces along the length:
The length of the steel sheet is given as 2400 mm, and each piece has a length of 300 mm. By dividing the total length by the length of each piece, we get 2400 mm ÷ 300 mm = 8. This means we can cut 8 pieces along the length of the steel sheet.
Calculate the number of pieces along the width:
The width of the steel sheet is given as 1200 mm, and each piece has a width of 200 mm. By dividing the total width by the width of each piece, we get 1200 mm ÷ 200 mm = 6. This means we can cut 6 pieces along the width of the steel sheet.
Calculate the total number of pieces:
To find the total number of pieces, we multiply the number of pieces along the length by the number of pieces along the width: 8 pieces × 6 pieces = 48 pieces.
Therefore, the correct answer is 48 pieces.
Learn more about Steel sheet here
https://brainly.com/question/32414525
#SPJ11
Help quickly!!! Will give points!!

Answers
Answer:
you need to show the examples
Step-by-step explanation:
Consider the function represented by the table.
What is f(0)?
04
O 5
06
O 7

Answers
Answer:
6
Step-by-step explanation:
From the table given defining a function, the values of "x" on the table represents the input of the function, which gives us an output, f(x), which can be labelled as "y" in some instances.
Thus, the value of f(0), is simply the output value we would get, given an input value of "0".
So therefore, f(0) = 6. That is, at x = 0, f(x) = 6.
Answer: 6
Step-by-step explanation:
One diagonal of a kite is four times as long as the other diagonal. If the area of the kite is 72 square meters, what are the lengths of the diagonals?
Answers
The lengths of the diagonals are 6 meters and 24 meters.
Let's start by assigning variables to the lengths of the diagonals. Let d₁ be the length of one diagonal and d₂ be the length of the other diagonal. We are given that one diagonal (let's say d₁) is four times as long as the other diagonal (d₂). So we can write:
d₁ = 4d₂
Next, we are given the area of the kite, which we can find using the formula:
Area = (1/2) x d₁ x d₂
Since we know the area is 72 square meters, we can plug in our variables and get:
72 = (1/2) x d₁ x d₂
Simplifying this equation, we can multiply both sides by 2 to get rid of the fraction:
144 = d₁ x d₂
Now we can substitute our expression for d₁ (4d₂) into this equation:
144 = 4d₂ x d₂
Simplifying again, we can combine like terms:
144 = 4d₂²
Dividing both sides by 4:
36 = d₂²
Taking the square root of both sides:
6 = d₂
Finally, we can use our expression for d₁ (4d₂) to find the length of the other diagonal:
d₁ = 4d₂ = 4 x 6 = 24
To know more about diagonal here
https://brainly.com/question/12274248
#SPJ1
11634 Ibm/h of a 80 weight% H2SO4 solution in water at 120F is continuously diluted with chilled water at 40F to yield a stream
containing 50 weight % H2SO4 at 140F. What is the rate of heat transfer in Btu/h for the mixing process? Assume that the chilled
water is saturated liquid.
Answers
The rate of heat transfer in Btu/h for the mixing process is given by Q = -9.282mi + 15000. The heat transfer rate, we can use the formula Q = mcΔT, where Q is the heat transferred, m is the mass, c is the specific heat, and ΔT is the change in temperature.
First, we need to calculate the mass and specific heat of the solution by applying mass balance and energy balance equations.
Mass balance:
mi = mf (1)
where mi is the mass flow rate of the initial solution, and mf is the mass flow rate of the final stream.
From the mass balance equation, we have:
mi = mf + mw (2)
where mw is the mass flow rate of water.
The weight percent of the solution can be expressed in terms of specific gravity (SG) using the equation:
w = [(SG - 1)/(SG + 1)] × 100
The specific gravity of the solution can be calculated using the equation:
SG = 1.0054 + 0.0005 × °API + 0.0012 × % H2SO4
The specific heat of the solution (cp) can be calculated using the equation:
cp = 0.4479 + 0.000125 * t
The mass flow rate of water is:
m w = 150 - mi [lb/h]
We will use the energy balance equation to calculate the rate of heat transfer:
Q = mi × cp × ΔTi + mW × cW × ΔTw
where ΔTi = 120 - 140 = -20°F (temperature drop of H2SO4 solution)
cP = 0.4479 + 0.000125 × 120 = 0.4629 Btu/lbm °F
Tw = 40 - 140 = -100°F (temperature drop of water)
cW = 1 Btu/lbm °F (specific heat of water)
So,
Q = (mi × 0.4629 × -20) + (150 - mi) × 1 × -100
Q = -9.258mi + 15000
Since the stream contains 50 weight% of H2SO4, the mass flow rate of the final stream, mf = mi, and the mass flow rate of water, mw = 150 - mi.
From equation (2):
mi + mw = mf
The final stream contains 50 weight% of H2SO4, therefore:
0.5 = [(SG - 1)/(SG + 1)] × 100
=> SG = 1.2
From the equation:
SG = 1.0054 + 0.0005 * °API + 0.0012 * %H2SO4
=> 1.2 = 1.0054 + 0.0012 × %H2SO4
=> %H2SO4 = 165
Therefore, the specific gravity of the final solution is 1.2 at 140°F. The specific heat of the final solution (cp) can be calculated using the equation:
cp = 0.4479 + 0.000125 * 140 = 0.4641 Btu/lbm °F
We will apply the energy balance equation to calculate the heat transfer rate:
Q = mi × cp × ΔTi + mW × cW × ΔTw
Q = (mi × 0.4641 × -20) + (150 - mi) ×
1 × -100
Q = -9.282mi + 15000
Learn more about heat transfer
https://brainly.com/question/13433948
#SPJ11
If 4 daps = 7 yaps, and 5 yaps = 3 baps, how many daps equal 42 baps? **GIVING OUT BRAINLIEST**
Answers
Answer:
40 daps
Step-by-step explanation:
lets say daps is d, yaps are y and baps are b
4d = 7y, 5y=3b
First convert to y
4/7d = y
Now convert that to b
5(4d/7) = 3b
20d / 7 = 3b
20d / 21 = b
Plug it in:
42(20d/21)
40d
aka 40 daps
If 15 people start a race, in how many different ways can the top 3 finishers be determined?
Answers
Hence, 15 people out of 3 people can be chosen in 35 ways.
Combinations:It is a method that helps us to determine the number of possible ways an item can be chosen given that the order of selection does not matter. Hence we are free to select the items in any order.Combinations are often confused with permutations. Permutations are the number of ways the given items can be arranged. Here the order is important.The formula for combinations:If we have 'n' items and we are required to choose 'r' items, the number of ways in which it can be done is calculated as:\(^{n}C_{r} }\) = \(\frac{n!}{(n-r)!r!}\)It is given that:
The total number of people in a race, n = 15
The number of finalists, r = 3.
Hence, the number of ways in which 3 people out of the 15 people can be finishers are:
\(^{15}C_{3} }\) = \(\frac{15!}{(15-3)!3!}\) = \(\frac{15!}{12!3!}\) = 35.
Hence, 15 people out of 3 people can be chosen in 35 ways.
For similar questions on permutations and combinations, visit:
https://brainly.com/question/13387529?referrer=searchResults
#SPJ4
If y varies directly with x and
y = 48 when x = 6, find y if x = 3.
First, find the direct variation equation.
y = [? ]x
Answers
so y=(k)x
sub y=48 and x=6
48=6k
k=8
now you got a constant k
now sub x=3
y=(8)(3)
=24
If profits decrease by 13.8% when the degree of operating
leverage (DOL) is 3.8, then the decrease in sales is:
A) 0.28%
B) 0.52%
C) 3.63%
D) 10%
E) 52.44%
Answers
Given that profits decrease by 13.8% when the degree of operating leverage (DOL) is 3.8.
The decrease in sales is: We have to determine the percentage decrease in sales Let the percentage decrease in sales be x.
Degree of Operating Leverage (DOL) = % change in Profit / % change in Sales3.8
= -13.8% / x Thus, we have: x
= -13.8% / 3.8
= -3.63%Therefore, the decrease in sales is 3.63%.Hence, the correct option is C) 3.63%. Percentage decrease in sales = % change in profit / degree of operating leverage
= 13.8 / 3.8
= 3.63% The percentage decrease in sales is 3.63%.
To know more about profits, visit:
https://brainly.com/question/29987711
#SPJ11
(state FB) Let A= ⎣
⎡
0
0
0
0
1
0
0
−3
0
1
0
−4
0
0
1
−10
⎦
⎤
,B= ⎣
⎡
0
0
0
1
⎦
⎤
Determine the matrix K so that the eigenvalues of A−BK are at −1,−1, −1+j, and −1−j.
Answers
The matrix K is \(\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&j&-j\\0&0&0&0\end{array}\right]\) .
The eigenvalues of A are the roots of the characteristic polynomial of A, which is:
det(A - xI) = (x + 1)(x + 3)(x + 4)(x + 10)
The eigenvalues of A are -1, -3, -4, and -10.
We want the eigenvalues of A - BK to be -1, -1, -1 + j, and -1 - j. The characteristic polynomial of A - BK is:
det(A - BK - xI) = (x + 1)(x + 1)(x + 1 + j)(x + 1 - j)
To make the eigenvalues of A - BK to be -1, -1, -1 + j, and -1 - j, we need to set the following equations equal to 0:
(x + 1)(x + 1) = 0
(x + 1 + j)(x + 1 - j) = 0
The first equation gives x = -1 and x = -1. The second equation gives x = -1 + j and x = -1 - j.
Therefore, the matrix K must be such that B * K = [-1, -1, -1 + j, -1 - j]T.
One possible matrix K is:
\(\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&j&-j\\0&0&0&0\end{array}\right]\)
This matrix satisfies the equation B * K = [-1, -1, -1 + j, -1 - j]T, so it is a possible value of K.
Another possible matrix K is:
\(\left[\begin{array}{cccc}0&0&j&-j\\1&0&0&0\\0&1&0&0\\0&0&0&0\end{array}\right]\)
This matrix also satisfies the equation B * K = [-1, -1, -1 + j, -1 - j]T, so it is also a possible value of K.
There are many other possible matrices K that satisfy the equation B * K = [-1, -1, -1 + j, -1 - j]T. The specific value of K that you choose will depend on your specific application.
To learn more about matrix here:
https://brainly.com/question/29132693
#SPJ4
Work out x^2- 2x
when x =4
Answers
Answer:
8
Step-by-step explanation:
\(x^2-2x \\x=4\\(4)^2-2(4)\\16-8\\8\)
A quadratic function is shown on the graph.
an upward opening parabola beginning with closed circle at negative 2 comma 4, which decreases to a vertex at 0 comma 0 and then increases to an open circle at 3 comma 9
What is the range of the function?
{x | −2 ≤ x < 3}
{x | −2 < x ≤ 3}
{y | 0 ≤ y < 9}
{y | 0 < y ≤ 9}
Answers
The range of the quadratic function is {y |0 ≤ y < 9}
What is the range of a function?The range of a function is the set of output values of the graph. This in other words mean the range of a function is the set of y values of the graph.
How to determine the range of the function?From the question, we have the following parameters:
The parabola opens upwardVertex = (0, 0)Closed circle point = (-2, 4)Open circle point = (3, 9)Write out the vertex
So, we have
Vertex = (0, 0)
Remove the x value
y = 0
From the question, we have
The parabola opens upward
This means that the vertex is a minimum
So, the range is
y ≥ 0
Rewrite as
0 ≤ y
Recall that:
Closed circle point = (-2, 4)
Open circle point = (3, 9)
Remove the x values
Closed circle point = 4
Open circle point = 9
Remove the smaller y value
Open circle point = 9
This means that the highest value of y is at open circle point = 9
This is represented as
y < 9
So, we have
0 ≤ y and y < 9
Combine both
0 ≤ y < 9
Rewrite properly as
{y |0 ≤ y < 9}
Hence, the range of the quadratic function is {y |0 ≤ y < 9}
Read more about range at
brainly.com/question/2264373
#SPJ1
{y |0 ≤ y < 9}
The person above need the shine, im just making it simple
Will Give Brainliest Help Please (Geometry )!!
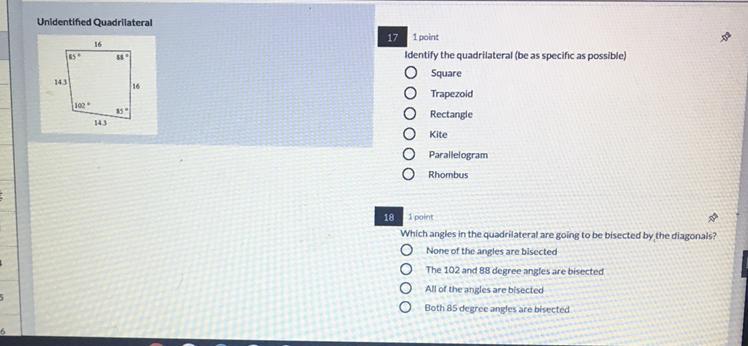
Answers
Answer:
17 is a Trapezoid, 18 is the last answer
HELP ME PLEASE Given that the universal set is all real numbers, write the complement of set A. Set A: {Irrational numbers}
Answers
Answer: The complement is Q, the set of the rational numbers.
Step-by-step explanation:
Ok, here we can use the fact that the set of all the real numbers is equal to the union of the set of the rational numbers and the set of the irrational numbers. (Remember that Q, the rational numbers, also does include the set of the integer numbers))
Then, if the universal set is R, we have that the universal set is:
R = Q + I
Where Q = set of rational numbers and I = set of irrational numbers.
Then, the complement of the set A = I = irrational numbers, is equal to:
R - I = Q + I - I = Q
Then the set of the rational numbers is the complement of the set A.
find all values of x in the interval [0, 2????] that satisfy the equation. (enter your answers as a comma-separated list.) 8 sin2(x) = 4
Answers
The values of x in the interval [0, 2π] that satisfy the equation 8sin(2x) = 4 are π/12 and 5π/12.
To find the values of x that satisfy the equation 8sin(2x) = 4 in the interval [0, 2π], we can solve for x by isolating sin(2x) first and then finding the corresponding angles.
Let's solve the equation step by step:
8sin(2x) = 4
Divide both sides of the equation by 8:
sin(2x) = 4/8
sin(2x) = 1/2
To find the values of x, we need to determine the angles whose sine is 1/2. These angles occur in the first and second quadrants.
In the first quadrant, the reference angle whose sine is 1/2 is π/6.
In the second quadrant, the reference angle whose sine is 1/2 is also π/6.
However, since we're dealing with 2x, we need to consider the corresponding angles for π/6 in each quadrant.
In the first quadrant, the corresponding angle is π/6.
In the second quadrant, the corresponding angle is π - π/6 = 5π/6.
Now, let's find the values of x in the interval [0, 2π] that satisfy the equation:
For the first quadrant:
2x = π/6
x = π/12
For the second quadrant:
2x = 5π/6
x = 5π/12
Therefore, the values of x in the interval [0, 2π] that satisfy the equation 8sin(2x) = 4 are π/12 and 5π/12.
So, the comma-separated list of values is π/12, 5π/12.
Learn more about trigonometric identities click;
https://brainly.com/question/24377281
#SPJ4
There is a bag filled with 3 blue and 4 red marbles. A marble is taken at random from the bag, the colour is noted and then it is not replaced. Another marble is taken at random. What is the probability of getting 2 reds?
Answers
Answer:
2/7
Altogether there're 7 marbles. Let,probability of getting blue and red marbles be 'B' and 'R' respectively.
In 1st pick
Probability of getting red marble is 4/7
So, there's the probability that the ball in 1st pick may be either blue or red.
So,if the marble is red then we've to eliminate that red marble ( cause,question says so)
Then,in 2nd pick
Probability of getting red ball will be 3/6(if we eliminate that red ball then the total number of marbles will also be 6)
Now,
Probability of getting two red will be
(4/7)×(3/6)
=2/7
It would be more easier to do by tree diagram. Since,I didn't find it convenient here,it may be not so much helpful.But, I tried my best. Hope you are clarified.
13) Choose the fraction that is equivalent to the given fraction.
4/5
○8/20
○16/20
○5/20
○2/20
Answers
Right Triangle Trigonometry (SOH CAH TOA) Mazes

Answers
Answer:for start
Step-by-step explanation:cos(28)=x over 19 than 19times cos(28)=x and x= 16.8
Use the Midpoint Rule with the given value of n to approximate the integral. Round the answer to four decimal places. 3 sin(x2) dx, n
Answers
The value of the given statement according to the mid point theorem is 5.
According to the statement
we have given that the equation and we have to integrate it with the help of the mid point theorem.
So, For this purpose, we know that the
The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
So, The given equation is
\(\int\limits^6_0 {Sinx } \, dx\)
where n = 4
And
The mid point formula is a with limits a to b is
f(x) dx ≈ Δx (f (x₀ + x₁)/2) + (f (x₁ + x₂)/2) + ... (f (xₓ₋₂ + xₓ₋₁)/2) + (f (xₓ₋₁ + x)/2))
Then
Where Δx = (b-a)/n
Recall that
a= 0
b= 64 and
n=4, therefore,
Δx = (64-0)/4 = 16
The next step requires that the interval [0,64] be divided into 4 sub-intervals with length = Δx =16
Hence, we've got, 0, 16, 32, 48, 64.
From this point, we calibrate the respective functions as follows:
f (x₀ + x₁)/2) = f ((0+16)/2) = f(8) = Sin (8) = 0.98935824662
(f (x₁ + x₂)/2) = f((16+32)/2) = f(24) =Sin (24) = -0.905578362
(f (x₂ + x₃)/2) = f((32+48)/2) = f(40) = Sin (40) = 0.74511316047
(f (x₃ + x₄)/2) = f((48+64)/2) = f(56) = Sin (56) = -0.52155100208
At this point, we sum up the above values derive the product of the total and Δx = 16
sin (x) dx = 16(0.98935824662 - 0.905578362 + 0.74511316047 - 0.52155100208)
= 16 (0.30734204301)
= 4.91747268816
\(\int\limits^6_0 {Sinx } \, dx = 5\)
So, The value of the given statement according to the mid point theorem is 5.
Learn more about Mid point theorem here
https://brainly.com/question/9635025
#SPJ4
The slope of the line below is -0.5. Enter the equation for the line in point-
slope form.
(1, 1)
Answers
The equation for the line in point-(1, 1) is y = -0.5x + 0.5.
Given that the slope of the line below is -0.5. We are to enter the equation for the line in point-(1, 1).The equation for the slope-intercept form of the line is y = mx + c where m is the slope and c is the y-intercept.
Now, the slope of the line is given as -0.5.Therefore, the equation for the slope-intercept form of the line is y = -0.5x + c. Now we need to find the value of c for the equation of the line.
To find the value of c, substitute the values of x and y in the equation of the slope-intercept form of the line.
Given that the point is (-1,1), x=-1 and y=1y = -0.5x + c⇒ 1 = (-0.5) (-1) + c⇒ 1 = 0.5 + c⇒ c = 1 - 0.5⇒ c = 0.5
Therefore, the equation for the line in point-(1, 1) is y = -0.5x + 0.5.The slope of a line refers to how steep the line is and is used to describe its direction. Slope is defined as the vertical change between two points divided by the horizontal change between them.A positive slope moves up and to the right, while a negative slope moves down and to the right. If a line has a slope of zero, it is said to be a horizontal line.
The slope-intercept form of a linear equation is y = mx + b, where m is the slope of the line and b is the y-intercept, or the point at which the line crosses the y-axis. To find the equation of a line with a given slope and a point, we can use the point-slope form of a linear equation.
Know more about linear equation here:
https://brainly.com/question/28732353
#SPJ8
PLS HELP ILL MARK YOU BRAINEST DUE SOON

Answers
Answer:
A, B, C, D or simplify all of them
Step-by-step explanation:
Answer:
all 4 of them
Step-by-step explanation:
a. 29x + 92 = 29x - 11
0x + 92 = -11
0x ≠ -103
b. 29x + 11 = 29x - 11
0x + 11 = -11
0x = -22
0 ≠ -22
c. 29x - 29 = 29x - 11
0x = 18
0 ≠ 18
d. 29x + 29 = 29x - 11
0x + 29 = -11
0x = -40
0 ≠ 40
PLEASE HEP ASAP GOT TEN MINS LEFT TILL DUE

Answers
Answer:
a ≈ 3.009075116
Step-by-step explanation:
cos(α) = adj/hyp
cos(53°) = a/5
a = 5 * cos(53°)
a ≈ 3.009075116
