Ruth's credit card has an APR of 10,91%, and it computes finance charges using the previous balance method on a
30-day billing cycle. During the April billing cycle, she made a $45.17 payment on April 10th and a $88.34 purchase on
April 17th. Her total at the start of May was $847.64. What was her balance at the beginning of April?
a $890.91
b. $797.22
C.$796.87
d. $804.47
Please select the best answer from the choices provided
Answers
Answer:
It's B trust
Step-by-step explanation:
The required balance at the beginning of April is $796.87. Option C is correct.
What is interest?Simple interest is defined as the percentage of earnings on the lending for a period of time
To determine Ruth's balance at the beginning of April, we can work backward from her total at the start of May.
Let's call Ruth's balance at the beginning of May "B".
We know that during the April billing cycle:
She made a $45.17 payment on April 10th
She made a $88.34 purchase on April 17th
The APR is 10.91%
So, B = B - $45.17 - $88.34 + (B * 0.1091 * 30 / 365)
Solving for B, we get:
B = $796.87
So, the answer is C. $796.87.
Learn more about your interest here:
https://brainly.com/question/20406888
#SPJ6
Related Questions
What kind of number is -2?
Rational
Irrational
Not a real number

Answers
- - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - -
\(\large\blue\textsf{\textbf{\underline{\underline{Question:-}}}}\)
What kind of number is \(\bold{-\sqrt{2}}\)?
\(\large\blue\textsf{\textbf{\underline{\underline{Answer and How to Solve:-}}}}\)
First, let's look at each of the four sets of numbers:-
Rational. This number set includes natural numbers (positive numbers only, like 1, 2, 3, 4, 5, 6...), zero, integers (negative & positive numbers and zero) and fractions (1/2, 1/3, 1/4...)Irrational. This set includes numbers that have an infinite quantity of digits after the decimal point. Also, irrational numbers cannot be written as fractions.Not a real number. This set includes imaginary numbers (yes, such numbers exist in mathematics, believe it or not)Natural number. As I said earlier, this set includes positive numbers only.So in which set does \(\bold{-\sqrt{2}}\) belong?
First, it's negative, so it's not a natural number.
Then, it's not an imaginary number, so it doesn't belong in the "Not a real number" set.
It can't be written as a fraction, so it doesn't belong in the "Rational" set, but it does belong in the "Irrational numbers" set.
According to the answer and explanation, we conclude that the number \(\bold{-\sqrt{2}}\) belongs in the "Irrational number" set.
Good luck.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
the net of a rectangle prism is shown below. the surface area of each face labled. which values represent the dimentions in meters of the rectangular prism
Answers
Verify each options
we have that
the base is 108 m2
so
6,18,54 could be
check
base=6x18=108 m2 is ok
but
the face of 18 m2 is not possible
check
2,9,12
9x12=108----> is ok
2x9=18 ----> is ok
2x12=24 ----> is ok
answer is 2,9,12
WILL GIVE BRAINLIEST PLEASR HELP ASAP
A set of 3 cards, spelling the word ADD, are placed face down on the table. Determine P(A, D) if two cards are randomly selected with replacement.
-In

Answers
Note that in the above Theoretical Probability prompt, the P(A, D) if two cards are randomly selected with replacement is 2/9. (Option C)
What is Theoretical Probability?
Theoretical probability is a branch of mathematics that deals with predicting the likelihood of events based on mathematical reasoning and assumptions, rather than empirical evidence or observations.
Where it is required to determine the P(A, D) if two cards are randomly selected from cards (A,D,D) with replacement:
P (A) = 1/3
P (D) = 2/3
Thus, P (A, D) = 1/3 * 2/3
= 1/3 × 2/3
= (1×2) / (3×3)
= 2/9
Thus, it is correct to state that the probability, if two cards A, and D are randomly selected with replacement is 2/9. (Option C)
Learn more about probability:
https://brainly.com/question/30604977
#SPJ1
You are given that z > 2. Write an inequality for each expression.
a) 2z+ 9
b) 3(z - 4)
c) 4+2z
d) 5(3z-2)
Answers
a) The inequality for the expression 2z + 9 is 2z + 9 > 13.
b) The inequality for the expression 3(z - 4) is 3z - 12 > -6.
c) The inequality for the expression 4 + 2z is 4 + 2z > 8.
d) The inequality for the expression 5(3z - 2) is 15z - 10 > 20.
a) To write an inequality for the expression 2z + 9, we can multiply the given inequality z > 2 by 2 and then add 9 to both sides of the inequality:
2z > 2 * 2
2z > 4
Adding 9 to both sides:
2z + 9 > 4 + 9
2z + 9 > 13
Therefore, the inequality for the expression 2z + 9 is 2z + 9 > 13.
b) For the expression 3(z - 4), we can distribute the 3 inside the parentheses:
3z - 3 * 4
3z - 12
Since we are given that z > 2, we can substitute z > 2 into the expression:
3z - 12 > 3 * 2 - 12
3z - 12 > 6 - 12
3z - 12 > -6
Therefore, the inequality for the expression 3(z - 4) is 3z - 12 > -6.
c) The expression 4 + 2z does not change with the given inequality z > 2. We can simply rewrite the expression:
4 + 2z > 4 + 2 * 2
4 + 2z > 4 + 4
4 + 2z > 8
Therefore, the inequality for the expression 4 + 2z is 4 + 2z > 8.
d) Similar to the previous expressions, we can distribute the 5 in the expression 5(3z - 2):
5 * 3z - 5 * 2
15z - 10
Considering the given inequality z > 2, we can substitute z > 2 into the expression:
15z - 10 > 15 * 2 - 10
15z - 10 > 30 - 10
15z - 10 > 20
Therefore, the inequality for the expression 5(3z - 2) is 15z - 10 > 20.
for such more question on inequality
https://brainly.com/question/17448505
#SPJ8
An isotope of the element seaborgium has a half-life is 30 seconds. How much would there be left after one minute if we started with 4 pounds? Show all your work.
Answers
Answer:
Step-by-step explanation:
PLEASE HELP!!!!!! i can't figure it out what does this mean??

Answers
for example, if a point was at (2,3) the translation would be (5,6) because you add 3
What is the answer pleaseee

Answers
Answer: 803.84cm3
Step-by-step explanation:
The formula for finding the volume of a cylinder is πr2h.
In other words, the area of the top face's circle times the height.
To find the circle's area, we first find the radius of the circle. Since the diameter is 8cm, we divide by 2 to get the radius, which is 4cm.
4cm squared is 4cm x 4cm, which is 16cm. 16cm times 3.14 is 50.24cm squared.
Now, we have the area of the circle. 50.24cm squared!
The height is 16cm, so to find the cylinder, we times the area of the circle by the height of the cylinder! So,
16cm x 50.24cm squared = 803.84cm cubed.
The volume of the can of soup is 803.84cm cubed.
Heather's work to find the distance between two points, R(-3,-4) and S(5,7), is
shown:
RS = √(-4) (-3))² + (7 − 5)²
= √(-1)² + (2)²
= √1 + 4
= √5
-
What error, if any, did Heather make?
A. She substituted incorrectly into the distance formula.
B. She subtracted the coordinates instead of adding them.
C. She made a sign error when simplifying inside the radical.
OD. She made no errors.

Answers
The distance between points R and S is \(\sqrt{ (185)\). The correct answer is D. She made no errors.
Heather's work to find the distance between two points, R(-3,-4) and S(5,7), is shown:
RS = √(-4) (-3))² + (7 − 5)²
= √(-1)² + (2)²= √1 + 4
= √5
The error is with the order of subtraction in the formula for the distance between two points.
Heather did not make any errors in calculating the distance between two points. Therefore, the correct answer to the question above is (OD) She made no errors.
The formula for the distance between two points, A (x1, y1) and B (x2, y2), in the coordinate plane is given as;
dAB = \(\sqrt{ ((x^2 - x1)^2 + (y2 - y1)^2)\)
Comparing the given question with the formula above, we have;
A = R (-3, -4) and B = S (5, 7)The distance, AB = RS.
Therefore, we have;
RS = \(\sqrt{ ((5 - (-3))^2 + (7 - (-4))^2)\)
On solving the above equation;RS = \(\sqrt{ ((5 + 3)^2 + (7 + 4)^2)\)RS
= \(\sqrt{ (8^2 + 11^2)RS\)
= \(\sqrt{ (64 + 121)RS\)
= \(\sqrt{ (185)\)
Therefore, the distance between points R and S is \(\sqrt{ (185)\).
From the calculation, it is clear that Heather did not make any errors while calculating the distance between two points. The answer obtained by Heather is correct.
For more questions on distance between
https://brainly.com/question/15958176
#SPJ8
Given the function:
f (x) = (3 x + 4) minus (2 minus x)
Evaluate for f (5).
Answers
Hope this helps!
Commitment to goals can be promoted in which of the following ways?
Answers
Commitment to goals can be promoted in through:
by imagining how you will feel when you achieve themby identifying who or what might keep you from achieving themWhat is goal commitment?Goal commitment is the degree of determination a person uses to achieve an accepted goal, and it is determined by two major factors: importance and self-efficacy. The reasons a person has for achieving a goal, including expectations of certain outcomes, are significant. Commitment helps you stick to your goals in both good and bad times, when obstacles arise. Commitment is influenced by two factors: importance and
Goal commitment is generally defined as an individual's determination to devote time and effort to achieving a goal.
Goal commitment is the degree of determination a person uses to achieve an accepted goal, and it is determined by two major factors: importance and self-efficacy. The reasons a person has for achieving a goal, including expectations of certain.
Learn more about goal on:
https://brainly.com/question/24693533
#SPJ1
1)
Science 5
Measurement Assignment
Name each measurement instrument below. Then, indicate which
type of measurement is performed with each one. Remember,
some instruments can be used for more than one type of
measurement!
Instrument
Name of Instrument
Measurement Type

Answers
Answer: See below
Step-by-step explanation:
The first is a beaker, it's used to measure liquid volume
The second is a ruler, it's used to measure length.
Last is a thermometer, it's used to measure temperature.
Penny Weights, use the weights of the post 1983 pennies to construct a 98% confidence interval estimate of the standard deviation of the weights of all post-1983 pennies. S=0.0165 n=37. Find confidence interval. a. 0.01231 < Ï < 0.2111 b. 0.01239 < Ï < 0.02111 c. 0.1391 < Ï < 0.2311 d. 0.001219 < Ï < 0.002111
Answers
Answer:
c. 0.1391 < Ï < 0.2311
Step-by-step explanation:
The formula for Confidence Interval is given as:
Mean ± z × Standard deviation/√n
Z score for 98% confidence interval = 2.326
Mean = Significance level = 100% - 98%
= 2% = 0.02
Standard deviation = S=0.0165
n= 37
Hence,
Confidence Interval =
0.02 ± 2.326 × 0.0165/√37
0.02 ± 0.0063094687
Confidence Interval
0.02 - 0.0063094687
= 0.1391
0.02 ± 0.0063094687
= 0.2311
Hence, the Confidence Interval = (0.1391, 0.2311)
= c. 0.1391 < Ï < 0.2311
GEOMETRY 100 POINTS
Find the length of BC

Answers
Answer:
x = 16
Step-by-step explanation:
Opposite sides are equal in a parallelogram
AD = BC
5x - 12 = 3x + 20
5x - 3x = 20 + 12
2x = 32
x = 32/2
x = 16
Find the indicated z score. The graph depicts the standard normal distribution with mean 0
and standard deviation 1.
The indicated z score is
(Round to two decimal places as needed.)
...
0.2776
20
Answers
Using the normal distribution, it is found that the indicated z-score is Z = 1.08.
What is mean by Percentage?A number or ratio that can be expressed as a fraction of 100 or a relative value indicating hundredth part of any quantity is called percentage.
Now, In a normal distribution with mean and standard deviation , the z-score of a measure X is given by:
z = (x - μ) / σ
Here, It measures how many standard deviations the measure is from the mean.
After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X.
In this problem, we want Z with a p-value of 0.2776,
Thus, we get;
⇒ z = 1.08.
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ1
A polynomial of the 5th degree with a leading coefficient of 7 and a constant term of 6
Answers
It can look like:
7x^5+2x^2+6
Or can even look like:
7x^5 + 6x^4 + 5x^3 + 4x^2 +6
In both equations, the polynomial is a 5th degree, with its leading coefficient as 7 and a constant term of 6.
Hope that helps!
Last year the depth of the river was 4.2 feet deep.
This year it dropped 5%.
Find the depth of the river this year to cross it.
Answers
Answer:
3.15 ツ
Step-by-step explanation:
A shipment of 8 computers contains 3 with defects. Find the probability that a sample of size 2, drawn from the 8, will not contain a defective computer.
What is the probability that a sample of 2 of the 8 computers will not contain a defective computer?
(Type an integer or a simplified fraction.)
Answers
Answer:
5/28
Step-by-step explanation:
First of all, probability is defined as the number of ways a certain event can happen divided by the total ways of an event happening. In this scenario, we are asked to find the number of non-defective computers divided by the total ways that a sample of two can be chosen.
The number of ways to choose 2 computers from 8 can be written as \(8\choose2\), which is equal to \(\frac{8\cdot7}{2}\), which is 28. Now, there are 3 defective computers, for a total of 5 non-defective computers, so the probability is 5/28.
what is the square root of -9?
Answers
9 is a perfect square
Tonya says that her favorite number is 44. Pena says that Tonya's number is 9 more than her favorite number.
Write an equation to represent the relationship between Tonya’s and Pena’s favorite
numbers.
Answers
Answer:
Let's assume Pena's favorite number as "p".
According to the problem, Tonya's number is 9 more than Pena's favorite number, so Tonya's favorite number would be p + 9.
But Tonya says her favorite number is 44, so we can write:
p + 9 = 44
This equation represents the relationship between Pena's and Tonya's favorite numbers.
Please someone help me I rlly don’t get this I’ll give you like 40 points

Answers
Answer:
Step-by-step explanation:
H(n)=91x(-1/7) n-1
do not know
Hope it helps the answer is the 2nd one have a great day

Find the area of a rectangle whose length is 14cm and breadth is 6cm

Answers
Answer:
Ellos dan las pistas de algunos problemas se pueden resolver de forma automática, los valores numéricos tienen ninguna importancia en los distintos ejemplos.
Traza 1
Uno de los lados de un rectángulo es 20 cm de largo; un segundo lado del rectángulo es de 0,85 m de largo. Calcular el perímetro y el área del rectángulo.
Traza 2
Calcular el área de un rectángulo cuyas dimensiones son 85 cm de largo y 20 cm respectivamente.
Traza 3
La base de un rectángulo es 20 cm de largo; la área es de 300 cm². Calcular la altura del rectángulo.
Traza 4
La altura de un rectángulo es 15 cm de largo; la área es de 300 cm². Calcula la base del rectángulo.
Traza 5
Un rectángulo tiene la altura que es de 3/8 de la base; la suma de las longitudes de los dos segmentos es 44 cm. Determinar el área del rectángulo y el perímetro.
Traza 6
La base de un rectángulo es de 0,40 m de largo; La altura del rectángulo es 30 cm. Calcular la diagonal.
Traza 7
Un tamaño de un rectángulo es un medio del lado de un cuadrado que tiene el perímetro de 20 cm. Sabiendo que los dos polígonos tienen el mismo perímetro, calcula la medida del tamaño del rectángulo.
Traza 8
La diagonal de un rectángulo es de 50 cm; la base es de 3/4 de la altura. Calcular el perímetro y el área del rectángulo.
Traza 9
La diagonal de un rectángulo mide 50 cm; ella es 5/3 de altura. Calcular el perímetro y el área del rectángulo.
Traza 10
Una mesa rectangular tiene lados de 180 cm y 90 cm respectivamente. Cuál es el perímetro y el área de un mantel que cuelga de 20 cm alrededor de la mesa?
Traza 11
Calcular el área de un rectángulo que tiene la altura 10 cm de largo, sabiendo que la medida de la base es el doble de la altura.
Traza 12
La diferencia entre el tamaño de un rectángulo es 12 cm y una es el triple de la otra. Calcular el área del rectángulo
Traza 13
La suma entre el tamaño de un rectángulo es 12 cm y una es el triple de la otra. Calcular el área del rectángulo
Traza 14
La suma de la base y la altura de un rectángulo es 50 cm; la base es superior a la altura de 4 cm. Calcular el área del rectángulo.
Traza 15
El semi-perímetro de un rectángulo es 32 cm y una dimensión es de 3/5 de la otra. Calcular el área del rectángulo.
Traza 16
El semi-perímetro de un rectángulo es 30 cm y una dimensión es igual a los sus 2/5. Calcular el área del rectángulo.
Traza 17
Un rectángulo tiene una base de 20 cm y una altura igual a 2/5 de la base. Calcular el perímetro y el área del rectángulo.
Traza 18
Un rectángulo tiene el área de 600 cm² y la base es 20 cm de largo. Cuál es su perímetro ?
Traza 19
Un rectángulo tiene un perímetro de 100 cm y la base es 30 cm de largo. Calcula su área.
Traza 20
Un rectángulo tiene un perímetro de 120 cm. Sabiendo que un tamaño es tres veces la otra, calcula el área del rectángulo.
Traza 21
La diferencia entre el tamaño de un rectángulo es 10 dm. Sabiendo que el perímetro es 100 dm, calcula el área del rectángulo.
Traza 22
Un rectángulo tiene un perímetro de 100 cm. Calcula su área sabiendo que la medida de la base es superior a la de la altura de 10 cm.
Traza 23
En el perímetro de un rectángulo es de 100 cm y la altura es de 20 cm de largo. Calcular el perímetro de un rectángulo equivalente a el mismo y que tiene su base de 40 cm de largo.
Traza 24
Un rectángulo es formado por dos cuadrados congruentes que tienen cada uno el perímetro de 24 cm. Calcular el perímetro y el área del rectángulo.
Traza 25
Un rectángulo es formado por tres cuadrados congruentes con cada lado 20 cm de largo. Calcular el perímetro y el área del rectángulo.
Traza 26
Un rectángulo es formado por dos cuadrados congruentes. Sabiendo que el perímetro del rectángulo es de 180 cm, calcular su área.
Traza 27
Un rectángulo y un cuadrado tienen el mismo perímetro. El lado de un cuadrado de 45 cm y las dimensiones del rectángulo son una 1/2 de la otra. Calcular el área del rectángulo.
Traza 28
Dos rectángulos son equivalentes. Sabiendo que las dimensiones de el primero miden respectivamente 30 cm y 20 cm, y que la base del segundo rectángulo es 40 cm de largo, calcula la diferencia entre los dos perímetros.
Traza 29
Calcular el perímetro de la figura y el área de la parte interior con la obtención de las medidas a partir del dibujo:
Traza 30
Calcular el perímetro de la figura y el área de la parte interior con la obtención de las medidas a partir del dibujo:
Traza 31
Un constructor ha comprado un terreno que tiene la planta mostrada en el dibujo y las dimensiones en metros se indican en la figura. Calcula el área y el perímetro de la tierra.
Traza 32
Una parcela de tierra tiene una forma rectangular con unas dimensiones de 50 m y de 30 m de largo. En el interior se ha construido una casa que ocupa una superficie rectangular de longitud 20 m y de 8 m de ancho. Calcular el área de la tierra permanecida libre.
Traza 33
Step-by-step explanation:
Answer:
A= 84cm
Step-by-step explanation:
length x width= area
plug in the given information.
14cm x 6cm = A
A=84
with a length of 14cm and a width of 6cm multiply them for an area of 84cm.
find the side of a cube whose surface area is 150² m
Answers
Answer:
6 m
Step-by-step explanation:
\(surface \: \: area = 4 {s}^{2} \)
s is side
\(150 = 4 {s}^{2} \\ {s}^{2} = 37.5 \\ s = 6.1 \: m\)
There are 6 identical square faces
Area of each face = 150 / 6 = 25 m^2
Edge length = sr(25) = 5 m
Which situation(s) has (have) a net result of zero?
Select ALL that apply.
The temperature was -5 °F and fell 5 degrees.
O Rich owed Peter $3 then spent $3.
A plane reaches an altitude of 15,000 feet then descends
15,000 feet.
D
Combine two atoms each with a charge of negative 2 and one atom
with a charge of positive 4.
D
Stephen deposited $100 in his bank account then bought a $100
coat.
Tameka drove from a city with an elevation of 39 feet to a city with
an elevation of 78 feet.
Answers
The situations that have a net result of zero are:
Rich owed Peter $3 then spent $3.Combine two atoms each with a charge of negative 2 and one atom with a charge of positive 4.Which situation(s) has (have) a net result of zero?The first situation results in a debt of $3 and then payment of $3, which cancels out the debt.
The second situation involves combining three atoms with a total charge of zero (2 atoms with a charge of negative 2, and 1 atom with a charge of positive 4).
Learn more about net result of zero here:https://brainly.com/question/30202590
#SPJ1
Pls help i will mark brainliest Determine the value of y for the inequality 4 times the quantity y plus one fifth end quantity is less than or equal to four fifths.
y ≥ 0
y ≤ 0
y is greater than or equal to negative 1 over 40
y is less than or equal to negative 1 over 40
Answers
The value of y is less than or equal to 0 (y ≤ 0).
What is inequality?
In mathematics, inequalities describe the relationship between two values that are not equal. Equal means to be equal, not. The "not equal symbol (≠)" is typically used to indicate that two values are not equal. But different inequalities are used to compare the values to determine whether they are less than or greater than.
Given:
4y + 1/5 ≤ 4/5
We have to find the value of y.
Subtract 1/5 from both sides,
4y + 1/5 - 1/5 ≤ 4/5 - 1/5
4y ≤ 3/5
Multiply both sides by 1/4
4y x 1/4 ≤ 3/5 x 1/4
y ≤ 3/20
y ≤ 0.15
Hence, the value of y is less than or equal to 0 (y ≤ 0).
To know more about inequality, click on the link
https://brainly.com/question/24372553
#SPJ1
Identify whether each function is linear or exponential.
Function A:
Function C
Function D:
You have $200 in
a savings
account that
earns 1% annual
interest
b. Which function has the greatest growth factor? Justify your response.

Answers
Answer:
A)
Function A: Exponential
Function B: Linear
Function C: Exponential
Function D: Exponential
B) Function A
Step-by-step explanation:
Function A: This is exponential because- (1, 3)(2,9)(3,27)
It is not going up by the same number each time. However, it is multiplying by 3 each time which means it is exponential.
Function B: This is linear because- (1, 64)(1, 80)(1, 96)
It is going up by 16 each time, (a constant number) which means it is linear.
Function C: This is exponential because- there is a curve, linear is always a straight line. But, this has a curve which means it is exponential.
Function D: This is exponential because- It is increasing by a percentage and not a constant number. It is increasing by 1% which means it is exponential.
The function that has the greatest growth factor is Function A because, Function A multiplies by 3 each time. Function B is linear, exponential functions always pass linear functions despite how "steep" they are. Eventually, the exponential function will surpass it. Function C is also exponential but is not as "steep" as Function A. Function A multiplies by 3 each time but Function C increases less. Function D is also exponential, and for the same reasons as Function C, Function A has the greatest growth factor.
Choose all of the numbers that make the statement true

Answers
Answer:
i'm pretty sure that the answer is B. 3/4
Step-by-step explanation:
3/4 X 2/3=1/2=0.5
2/3= 0.666666667
=> 1/2 (0.5) < 2/3 (0.6667)
=> 3/4 X 2/3 < 2/3
PLEASE HELP
-10+7/4p=-38
Show your work in details if you can, I have a hard time understanding this.
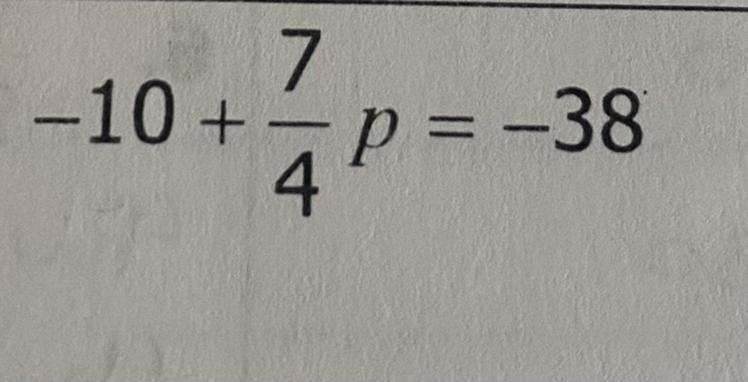
Answers
Answer:
Here is your answer . Hope it helps you
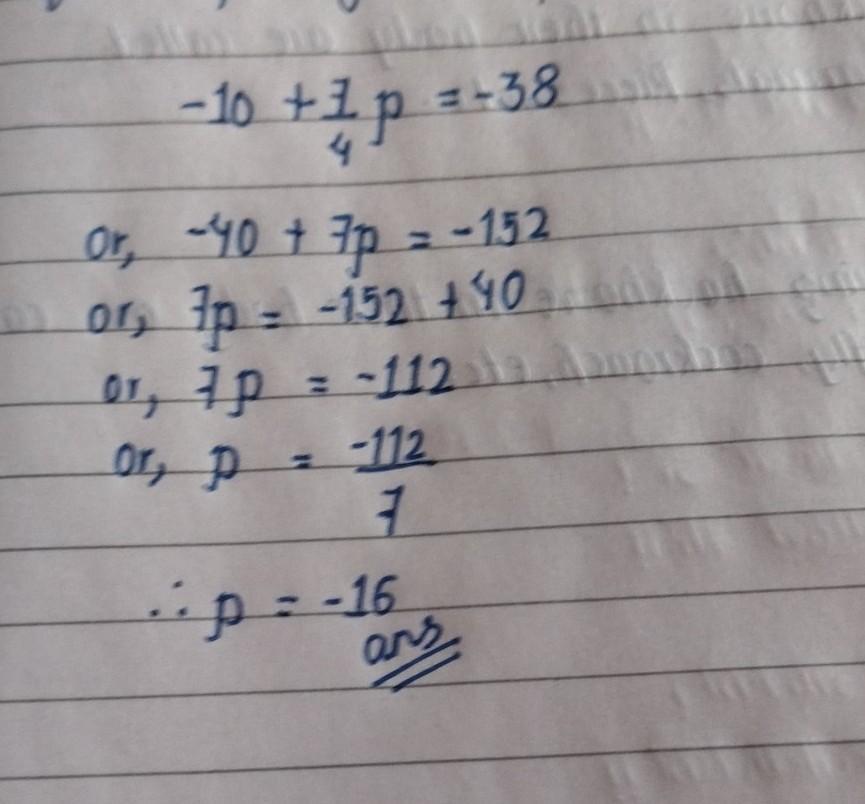
Answer:
p = -49
Step-by-step explanation:
-10 + 7/4p = -38
+7/4 p = -38 + 10. ..........(-10 taken to other side)
+7/4 p = -28
p = -28 × 7/4 ........( now taken 7/4 to other side)
p = -196/4 .......(here we have multiplied . (-28×7 )
p = -196/4
p = -49
so p = -49
MARK AS BRAINLIST IF IT IS USEFUL
Find the amount (future value) of the ordinary annuity. (Round your answer to the nearest cent.)
$300/week for 9 1/2
years at 5.5%/year compounded weekly
Answers
Answer: $227,226.51
Step-by-step explanation:
First, we need to convert the period to weeks.
9 1/2 years = 9.5 years
1 year = 52 weeks
9.5 years = 494 weeks
Next, we can use the formula for the future value of an annuity:
FV = (PMT x (((1 + r/n)^(n*t)) - 1)) / (r/n)
where:
PMT = payment amount per period
r = annual interest rate
n = number of compounding periods per year
t = number of years
Plugging in the given values:
PMT = $300
r = 0.055 (5.5% expressed as a decimal)
n = 52 (compounded weekly)
t = 9.5 years = 494 weeks
FV = ($300 x (((1 + 0.055/52)^(52*494)) - 1)) / (0.055/52)
FV = $227,226.51
Therefore, the future value of the annuity is approximately $227,226.51.
Ignore the partner part i need this ASAP

Answers
The Slope of the line is the coefficient of x and the y co-ordinate of the equation is the constant value in the equation.
What is a Slope of a line?
A slope of a line is defined in mathematics as the change in y coordinate with regard to the change in x coordinate. The net change in y-coordinate is denoted by Δy, whereas the net change in x-coordinate is denoted by Δx. As a result, the change in y-coordinate in relation to the change in x-coordinate is given by,
m = difference in y/difference in x = Δy/Δx
Where "m" represents the slope of a line.
Solution:
we know that a general from of equation of straight line is y = mx + c where m is the slope.
3. y = -x + 2 = It is a line = Slope is -1 = (0,2)
4. y = -x - 2 = It is a line = Slope is - = (0, -2)
5. y = 1/2x + 1 = It is a line = Slope is 1/2 = (0, 1)
6. y = x +2 = It is a line = Slope is 1 = (0, 2)
7. y = x - 2 = It is a line = Slope is 1 = (0, -2)
8. y = 1/2x - 1 = It is a line = Slope is 1/2 = (0, -1)
9. y = -1/2x - 1 = It is a line = Slope is -1/2 = (0, -1)
10. y = 3x + 2 = It is a line = Slope is 3 = (0, 2)
11. y = 3x - 2 = It is a line = Slope is 3 = (0, -2)
12. y = -2x + 3 = It is a line = Slope is -2 = (0, 3)
To learn more about Slope of a Straight Line from the given link
https://brainly.com/question/20898425
#SPJ1
You can use the notation P(A), read “the probability of event B, given event A” to write a
A. Probability distribution
B. Frequency table
C. Conditional probability
D. Cumulative probability
Answers
You can use the notation P(A), read “the probability of event B, given event A” to write a conditional probability. The correct answer is C.
Conditional probability refers to the probability of one event occurring given that another event has already occurred. In this case, we are interested in the probability of event B occurring given that event A has already occurred, and we can represent this using the notation P(B|A), where '|' means 'given'.
For example, let's say we are interested in the probability of getting a head on a coin toss (event B), given that the coin was flipped and landed on heads (event A). We could represent this using the notation P(B|A). The value of P(B|A) would be 1, because if the coin already landed on heads, then the probability of getting a head on the next flip is certain.
Conditional probability is an important concept in probability theory and is often used in real-world applications, such as predicting the likelihood of a disease given certain symptoms, or the probability of an event occurring given certain conditions.
The correct answer is C.
To learn more about probability click on,
https://brainly.com/question/29259732
#SPJ1