Ryan and his children went into a bakery and will buy cupcakes and brownies. Each cupcake costs $4.75 and each brownie costs $1. Ryan has a total of $50 to spend on cupcakes and brownies. Write an inequality that would represent the possible values for the number of cupcakes purchased, cc, and the number of brownies purchased, b.b.
Answers
Answer: 4.75c+1b ≤50
Step-by-step explanation: One cupcake costs $4.75, so “c” cupcakes cost $4.75. One brownie cost $1, so “b” brownies cost 1b. The total 4.75c+1b must be less or equal to $50.
Related Questions
WILL GET BRAINLY
the equation has and . a valid solution for x is
Answers
Answer:
Is there supposed to be a attachment. because I dont see anything
Step-by-step explanation:
a.
Subtract: 7a-5b + 4c from 3a + 3b - 70
b. Solve: 5x + 1 = 2x + 7
please I need the answer ASAP
Answers
Answer:
a. 4a−8b+4c+70
b. x=2
Step-by-step explanation:
\(a. \: (7a−5b+4c)−(3a+3b−70)\)
\(7a−5b+4c−(3a)−(3b)−(−70)\)
\(7a−5b+4c−3a−3b+70\)
\(4a−5b+4c−3b+70\)
\(4a−8b+4c+70\)
b. Let's solve your equation step-by-step.
5x+1=2x+7
Step 1: Subtract 2x from both sides.
5x+1−2x=2x+7−2x
3x+1=7
Step 2: Subtract 1 from both sides.
3x+1−1=7−1
3x=6
Step 3: Divide both sides by 3.
\( \frac{3x}{3} = \frac{6}{3} \)
x=2
Hope it is helpful....Chloe is trying to find three consecutive, positive integers such that six times the largest is equal to the twice sum of the two smaller integers. Show that the three consecutive, positive integers 4, 5, and 6 are not the ones Chloe is looking for.
Answers
Answer:
The three consecutive numbers cannot be 4, 5, and 6 because, the result will be 36 ≠ 18, which is indeterminate
Step-by-step explanation:
The given parameters are;
The three consecutive positive numbers Chloe is trying to find are x, x+1, x + 2
The conditions of the three positive numbers are;
6 × (x + 2) = 2 × (x + x + 1)
We check if the three consecutive numbers can be 4, 5, and 6 by substituting the values as follows;
x + 2 = 6
x + 1 = 5
x = 4
Which gives;
6 × (6) ≠ 2 × (4 + 5)
36 ≠ 18
Therefore, the three consecutive numbers cannot be 4, 5, and 6
Parv has a $50 gift card he uses the gift card to buy a pack of games for 9. 99. He also wants to buy n movies. Each movie cost 3. 99. Which inequality describes how many movies part can buy?
Answers
The inequality that describes how many movies Parv can buy is: n ≤ 10.025
Let's denote the number of movies Parv wants to buy as n. We are given that each movie costs $3.99. To determine the inequality that describes how many movies Parv can buy, we need to consider the amount of money he has remaining after purchasing the pack of games.
Parv starts with a $50 gift card and spends $9.99 on a pack of games. The remaining amount on the gift card is $50 - $9.99 = $40.01.
Now, let's consider the cost of n movies. Each movie costs $3.99, so the total cost of n movies would be n * $3.99.
Since Parv wants to buy the movies using the remaining amount on his gift card, we can set up the inequality:
n * $3.99 ≤ $40.01
This inequality states that the total cost of n movies, represented by n * $3.99, must be less than or equal to the remaining amount on the gift card, which is $40.01.
Simplifying the inequality further, we have:
3.99n ≤ 40.01
Now, if we want to solve for n, we can divide both sides of the inequality by 3.99:
n ≤ 40.01 / 3.99
Calculating this value, we have:
n ≤ 10.02506265664
Therefore, the inequality that describes how many movies Parv can buy is:
n ≤ 10.025
This means that Parv can buy a maximum of 10 movies, as he cannot purchase a fractional part of a movie.
for more such question on inequality visit
https://brainly.com/question/30238989
#SPJ8
Find the area
Help me please

Answers
Answer:
72
Step-by-step explanation:
You add the base which is 8 and 18 then multiply by 11 which is 144. after that you divide by two and get your answer 72
________________pproaches to risk calculation typically assigns a numeric value (1–10) or label (high, medium, or low) to represent a risk.
Answers
Answer:
Step-by-step explanation o:
Sample statistics and population parameters A researcher is interested in knowing the average height of the men in a village. To the researcher, the population of interest is the - in the village, the relevant population data are the in the village, and the population parameter of interest is the There are 780 men in the village, and the sum of their heights is 4,617.6 feet. Their average height is feet. Instead of measuring the heights of all the village men, the researcher measured the heights of 13 village men and calculated the average to estimate the average height of all the village men. The sample for his estimation is , the relevant sample data are the , and the sample statistic is the If the sum of the heights of the 13 village men is 79.3 feet, their average height is feet.
Answers
A researcher is interested in knowing the average height of the men in a village. To the researcher, the population of interest is the men in the village.
the relevant population data are the heights of all men in the village, and the population parameter of interest is the average height of all men in the village there are 780 men in the village, and the sum of their heights is 4,617.6 feet. Therefore, the average height of all the men in the village is:
Average Height = Sum of Heights / Number of Men
Average Height = 4,617.6 feet / 780 min
Average Height = 5.92 feet
Instead of measuring the heights of all the village men, the researcher measured the heights of 13 village men and calculated the average to estimate the average height of all the village men. The sample for his estimation is the 13 village men, the relevant sample data are their heights, and the sample statistic is the average height of the 13 village men If the sum of the heights of the 13 village men is 79.3 feet, their average height is:
Average Height (sample) = Sum of Heights (sample) / Number of Men (sample)
Average Height (sample) = 79.3 feet / 13 min
Average Height (sample) = 6.10 feet.
To know more about average height:- https://brainly.com/question/30302355
#SPJ11
convert to slope intercept form to graph 4x + 3y = 9
Answers
Answer:
y=-4/3x+3
Step-by-step explanation:
Find the area of the region that lies inside the circle r = 9 sin(theta) and outside the cardioid r = 3 + 3 sin(theta). The cardioid (in blue) and the circle (in red) are sketched in the figure. The value of a and b in this formula are determined by finding the points of intersection of the two curves. They intersect when 9 sin(theta) = 3 + 3 sin(theta), which gives sin(theta) = 1/2, so theta = pi/6, theta = 5 pi/6. The desired area can be found by subtracting the area inside the cardioid between theta = pi/6, 5 pi/6 from the area inside the circle from pi/6 to 5 pi/6. Thus A = 1/2 integral_pi/6^5 pi/6 (9 sin (theta))^2 d theta - 1/2 integral_pi/6^5 pi/6 (3 + 3 sin (theta))^2 d theta Since the region is symmetric about the vertical axis theta = pi/2, we can write A = 2[1/2 integral_pi/6^pi/2 81 sin^2 (theta) d theta - 9/2 integral_pi/6^pi/2 (1 + 2 sin (theta)) d theta] = integral_pi/6^pi/2 [72 sin^2(theta) - 9 - d theta] = integral_pi/6^pi/2 (-36 cos (2 theta) - sin (theta)) d theta [because sin^2 (theta) = 1/2 (1 - cos (2 theta))] =|_pi/6^pi/2 =
Answers
Therefore, the area of the region inside the circle and outside the cardioid is. \(2\sqrt(3)\).
To find the area of the region inside the circle and outside the cardioid, we need to integrate the difference between the areas of the circle and the cardioid over the interval where they intersect. The points of intersection are at theta = pi/6 and theta = 5pi/6, as given in the problem.
First, let's find the equation of the cardioid in Cartesian coordinates. We have r = 3 + 3sin(θ), so in Cartesian coordinates, this is:
\(x^2 + y^2\)= \((3 + 3sin(θ)) ^2\)
\(x^2 + y^2\)= \(9 + 18sin(θ) + 9sin^2(θ)\)
\((x^2 + y^2 - 9)\) = \(18sin(θ) + 9sin^2(θ)\)
Using the equation of the circle, r = 9sin(theta), we can rewrite sin(theta) as r/9:
(\(x^2 + y^2 - 9) = 18(r/9) + 9(r/9)^2\)
\(x^2 + y^2 = 3r + r^2/3\)
Now we can set up the integral to find the area:
A = 1/2 ∫\((pi/6) ^{(5\pi/6)} [81sin^2(θ) - 9 - 18sin(θ) - 9sin^2(θ)] dθ\)
\(A = 1/2 ∫(pi/6)^(5pi/6) [72sin^2(θ) - 9 - 18sin(θ)] dθ\)
Since the region is symmetric about the vertical axis theta = pi/2, we can double this integral:
A = ∫\((pi/6)^(pi/2) [72sin^2(θ) - 9 - 18sin(θ)] dθ\)
Now we can use the identity sin^2(θ) = 1/2(1 - cos(2θ)) to simplify the integral:
A = ∫\((\pi/6) ^(pi/2) [36(1-cos(2θ)) - 9 - 18sin(θ)] dθ\)
A = ∫\((pi/6) ^(\pi/2) [-36cos(2θ) - sin(θ)] dθ\)
Integrating, we get:
A = [-\(18sin(2θ) - cos(θ)] |_\pi/6^\pi/2\)
\(A = [-18sin(2(\pi/2) - 2(\pi/6)) - cos(\pi/2) + cos(\pi/6)] - [-18sin(2(\pi/6)) - cos(\pi/6)]\)
\(A = [-18sin(\pi /3) - 0.5] - [-9\sqrt(3)/2 - sqrt(3)/2]\)
\(A = -18\sqrt(3)/2 + 4.5 + 9\sqrt(3)/2 - \sqrt(3)/2\)
\(A = 4\sqrt(3)/2\)
\(A = 2\sqrt(3)\)
To know more about vertical axis visit:
https://brainly.com/question/24439946
#SPJ1
Jayla and her mom are making a cake.
They add % c flour and 3/2 c sugar.
:)
If the total amount of batter is 4 lc,
how many cups of other ingredients
are included?
The text in the bottom of the v=10 is what I’m confused in

Answers
Answer:
Other ingredients is 2
v =10 is the answer of 5th question (-40)/-4 = 10
Step-by-step explanation:
I. Find sum of flour and sugar
when c is cup, flour = 3/4 and sugar is 3/2
\(\frac{3}{4} +\frac{3}{2} = \frac{9}{4}\) or \(2\frac{1}{4}\)
II. If total is \(4\frac{1}{4}\)
so \(4\frac{1}{4} - 2\frac{1}{4}\) = 2
Hope that help :D
11. The line of best fit through a set of data is y=-22.989-0.456x According to this equation, what is the predicted value of the dependent variable when the independent variable has value 40? y= Round to 1 decimal place. 13. The line of best fit through a set of data is y=4.985-2.012x According to this equation, what is the predicted value of the dependent variable when the independent variable has value 20? y Round to 1 decimal place. 18. The line of best fit through a set of data is y=19.116-2.936x According to this equation, what is the predicted value of the dependent variable when the independent variable has value 130? ya Round to 1 decimal place.
Answers
The predicted value of the dependent variable is -364.444 when the independent variable has value 130.
11. When x = 40, then
y =-22.989-0.456(40)
= -40.059.
The predicted value of the dependent variable is -40.059 when the independent variable has value 40.
13. When x = 20, then
y =4.985-2.012(20)
= -34.055.
The predicted value of the dependent variable is -34.055 when the independent variable has value 20.
18. When x = 130, then
y =19.116-2.936(130)
= -364.444.
The line of best fit is a straight line that comes closest to the data on a scatter plot with the least squares. It shows the relationship between two variables represented by x and y.
This line has an equation y = mx + b.
Here, m is the slope of the line, and b is the y-intercept.
The slope represents the rate of change of the variable on the y-axis concerning the variable on the x-axis.
The intercept indicates the value of the dependent variable when the independent variable is equal to zero.
To calculate the predicted value of the dependent variable y when the independent variable x has a specific value, plug in the value of x in the equation of the line of best fit and then solve the equation for y.
The resulting value of y is the predicted value of the dependent variable.
To know more about decimal visit:
https://brainly.com/question/33109985
#SPJ11
The shaded region under a Normal distribution with mean 100 and standard deviation 5 is shown. Which of the following is the best choice that corresponds to the shaded region? Select one.
Question 4 options:
Probability of x ≤ 92
Probability of x ≤ 108
Probability of x ≥ 92
Probability of x ≥ 108
Answers
The chance of x 92 is the best option since it corresponds to the shaded area under a normal distribution with a mean of 100 and a standard deviation of 5.
Identify the mean (μ) and standard deviation (σ),
Here, mean μ = 100, standard deviation σ = 5
Recognize that x = 92 is within the shaded region of normal distribution, so the probability we're looking for is either x ≤ 92 or x ≥ 92.
Since the shaded region is to the right of 92, the best choice is the probability of x ≥ 92.
Learn more about "Normal distribution": https://brainly.com/question/4079902
#SPJ11
In a sample of 1000 U.S. adults, 150 said they are very confident in the nutritional information on restaurant menus. Four U.S adults are selected at random without replacement (a) Find the probability that all four adults are very confident in the nutritional information on restaurant menus (b) Find the probability that none of the four adults are very confident in the nutritional information on restaurant menus 0.522 (c) Find the probability that at least one of the four adults is very confident in the nutritional information on restaurant menus 0.478
Answers
(a)The probability that all four adults are very confident is approximately 0.0056.
(b) The probability that none of the adults are very confident is approximately 0.522.
(c) The probability that at least one adult is very confident is approximately 0.478.
What is the probability of selecting four adults at random without replacement from a sample of 1000 U.S. adults, given the proportion of very confident individuals?
The probability of selecting four adults at random without replacement from a sample of 1000 U.S. adults depends on the proportion of very confident individuals. By calculating the probability of all four adults being very confident (a), none of the four adults being very confident (b), and at least one of the four adults being very confident (c), we can determine the likelihood of these scenarios occurring based on the given information.
To solve this problem, we can use the concept of probability and combinations.
(a)Given that there are 150 out of 1000 U.S. adults who are very confident, the probability of selecting one adult who is very confident is:
P(very confident) = 150/1000
= 0.15
Since the sampling is done without replacement, after each selection, the sample size decreases by 1. Therefore, for the second selection, the probability becomes 149/999, for the third selection, it becomes 148/998, and for the fourth selection, it becomes 147/997.
To find the probability that all four adults are very confident, we multiply these probabilities together:
P(all four adults are very confident) = (0.15) * (149/999) * (148/998) * (147/997)
≈ 0.0056
(b) The probability of selecting one adult who is not very confident (opposite of very confident) is:
P(not very confident) = 1 - P(very confident)
= 1 - 0.15
= 0.85
Since we are selecting four adults at random without replacement, the probability of none of them being very confident can be calculated as:
P(none very confident) = P(not very confident) * P(not very confident) * P(not very confident) * P(not very confident)
= (0.85)* (0.85) * (0.85) * (0.85)
≈ 0.522
(c) The probability of at least one adult being very confident is the complement of none of them being very confident:
P(at least one very confident) = 1 - P(none very confident)
= 1 - 0.522
= 0.478
Therefore,
(a) The probability that all four adults are very confident is approximately 0.0056.
(b) The probability that none of the adults are very confident is approximately 0.522.
(c) The probability that at least one adult is very confident is approximately 0.478.
To learn more about the probability from the given link
brainly.com/question/13604758
#SPJ4
if you could get the answer with a short explanation that would be great!

Answers
Answer:
3x+1 is the correct answer

Answer:
3x + 1
Step-by-step explanation:
3x + 1
x - 5 I 3x² - 14x - 5 3x²÷x = 3x; (x-5)*3x = 3x² - 15x
3x² - 15x Subtract
- +
0 + x - 5 x ÷x = 1 ; (x -5)*1 = x - 5
x - 5 Subtract
- +
0
32% is the same as 79 million tons. What is total
Answers
Answer:
225 tons is the total
Step-by-step explanation:
Let the total amount be x
Given that,
32% of x = 72tons
32x/100 = 72tons
32x = 7200tons
x = 225 tons
To verify,
32% of 225 = 72tons
32/100 * 225 = 72 tons
72 = 72
Hence, verified.
A scientific observation must be which of the following?a. reproducibleb. uniquec. previously unobservedd. supportive of the hypothesis in question
Answers
A scientific observation must be reproducible (option a).
A scientific observation must be reproducible, meaning that the results can be consistently obtained by multiple researchers or through repeated experiments. Reproducibility is a fundamental principle of scientific research as it allows for independent verification and validation of observations.
It ensures that the observed phenomenon or data is not a chance occurrence or influenced by individual biases. By reproducing the observation, scientists can establish the reliability and robustness of the findings. The correct option is a.
To know more about reproducible:
https://brainly.com/question/27983325
#SPJ4
what ac is equal to

Answers
Answer:
AC = 10
Step-by-step explanation:
Formula
(x + 1) + (x + 3) + 2x = 40 Remove the brackets
Solution
x + 1 + x + 3 + 2x = 40 Collect like terms
4x + 4 = 40 Subtract 4 from both sides
4x +4 -4 = 40 - 4 Combine
4x = 36 Divide both sides by 4
4x/4 = 36/4
x = 9
AC = x + 1
AC = 9 + 1
AC = 10
Rebecca earns $4250 per month, of which 24% is taken out of her paycheck for federal and state income taxes and other required deductions. Last month she spent $975 fir rent and $317 for food. What percent of her take-home pay did she spend on rent and rood combined?
Answers
The answer is 3,162
I got it by adding what I got from when I subtracted and then I added up all the things here's the work 1870+975+317=3,162
Answer:
40%
Step-by-step explanation:
subctract taxes by multiplying the total earnings by the tax rate (.24) leaving rebecca with $3230. then divide her food/rent costs by what she has left (3230)
=0.4 ; 40%
Please help with practice question
Write the following equation in slope-intercept
form: x + 5y = 30
Answers
Answer:
y = -1/5x + 6
Step-by-step explanation:
y=mx+b
hope this helps :)
help ?? Nancy found that x=1 is one solution to the quadratic equation (x+2)2=a. What is the value of a?
a.) -9
b.) -3
c.) 3
d.) 9
Answers
Answer:
Anwer- 9
Step-by-step explanation:
(1+2)2 =6 but since there isnt 6, go for 9.
- Hope this helps a little
The value of a from the given quadratic equation is 9. Therefore, option D is the correct answer.
What is the solution of a quadratic equation?The solutions to the quadratic equation are the values of the unknown variable x, which satisfy the equation. These solutions are called roots or zeros of quadratic equations. The roots of any polynomial are the solutions for the given equation.
Given that, Nancy found that x=1 is one solution to the quadratic equation (x+2)²=a.
Now, substitute x=1 in the equation (x+2)²=a, that is
(1+2)²=a
a=3²
a=9
Therefore, option D is the correct answer.
To learn more about the solution of quadratic equation visit:
https://brainly.com/question/18305483.
#SPJ6
Write an equation in slope-intercept form for the line with slope
\( - \frac{3}{2} \)
and y-intercept 5.
Answers
The equation in slope-intercept form for the line is y = -3/2x + 5.
We have,
In slope-intercept form,
The equation of a line is written as y = mx + b, where m represents the slope of the line and b represents the y-intercept (the point where the line crosses the y-axis).
Given that the slope is -3/2 and the y-intercept is 5, we can substitute these values into the equation to obtain:
y = -3/2x + 5.
This equation tells us that for every increase of 1 unit in the x-coordinate, the y-coordinate decreases by 3/2 units.
The y-intercept of 5 indicates that the line passes through the point (0, 5).
Thus,
The equation in slope-intercept form for the line is y = -3/2x + 5.
Learn more about equation of a line here:
https://brainly.com/question/23087740
#SPJ1
Please answer and explain

Answers
Answer:
Hi, don't stress this is very easy! So basically, since those segments are equal, you would have to equate them meaning inverse operations. So 3x-4=x+12
The answer would therefore, be x=8
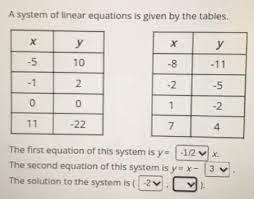
Select the correct answer from each drop-down menu. A system of linear equations is given by the tables. x y -5 10 -1 2 0 0 11 -22 x y -8 -11 -2 -5 1 -2 7 4 The first equation of this system is y = x. The second equation of this system is y = x − . The solution to the system is ( , ).
Answers
For the linear equations provided by the coordinates in the table;
The first equation of this system is y = -2x.
The second equation of this system is y = x - 3.
The solution to the system is (1, -2).
How do we solve for the system of linear equation?We have four points (-5,10), (-1,2), (0,0), and (11,-22) for first equation, and four points (-8,-11), (-2,-5), (1,-2), and (7,4) the second equation.
The slope (m) is given by the formula (y2 - y1) / (x2 - x1).
For the first line, we can use the points (-5,10) and (-1,2)
m1 = (2 - 10) / (-1 - (-5)) = -8/4 = -2.
the first equation is y = -2x
the second line, we can use the points (-8,-11) and (-2,-5)
m2 = (-5 - -11) / (-2 - -8) = 6/6 = 1.
the second line has a slope of 1,
the equation should have the form y = x + c.
To find c, we can use one of the points, for instance (-2,-5):
-5 = -2 + c => c = -5 + 2 = -3.
So, the second equation is y = x - 3.
the solution to the system, we need to find where the two lines intersect.
y = -2x
y = x - 3
Setting both equation equally
-2x = x - 3
=> 3x = 3
=> x = 1.
Substituting x = 1 into the first equation
y = -2(1) = -2.
the solution to the system of linear equation would be (1, -2).
Find more exercises on linear equation;
https://brainly.com/question/29739212
#SPJ1
for every lion there are 7 giraffes
Answers
Answer:
.................
Step-by-step explanation:
hmmm
?
Answer:
7 times however many lions they have
Step-by-step explanation:
What are all of the solutions to the equation (cos θ)(cos θ) + 1 = (sin θ)(sin θ)?
Answers
Answer: Starting with the given equation:
(cos θ)(cos θ) + 1 = (sin θ)(sin θ)
We can use the identity cos² θ + sin² θ = 1 to rewrite the right-hand side:
(cos θ)(cos θ) + 1 = 1 - (cos θ)(cos θ)
Combining like terms, we get:
2(cos θ)(cos θ) = 0
Dividing both sides by 2, we get:
(cos θ)(cos θ) = 0
Taking the square root of both sides, we get:
cos θ = 0
This equation is true for θ = π/2 + kπ, where k is any integer. So the solutions to the equation are:
θ = π/2 + kπ, where k is any integer.
Enjoy!
Step-by-step explanation:
We can use the trigonometric identity cos²θ + sin²θ = 1 to manipulate the given equation:
cos²θ + 1 = sin²θ
Subtracting cos²θ from both sides, we get:
1 = sin²θ - cos²θ
Using the identity sin²θ - cos²θ = sin(θ + π/2)sin(θ - π/2), we can simplify the right-hand side:
1 = sin(θ + π/2)sin(θ - π/2)
Now we can use the product-to-sum identity sin(θ + π/2)sin(θ - π/2) = (1/2)[cos(θ - (-π/2)) - cos(θ + π/2)] to further simplify the equation:
1 = (1/2)[cos(θ + π) - cos(θ)]
Since cos(θ + π) = -cos(θ), we can substitute into the equation:
1 = (1/2)[-cos(θ) - cos(θ + π/2)]
Using the identity cos(θ + π/2) = -sin(θ), we get:
1 = (1/2)[-cos(θ) + sin(θ)]
Multiplying both sides by 2, we get:
2 = -cos(θ) + sin(θ)
Rearranging, we get:
cos(θ) + sin(θ) = 2
Now we can use the identity cos(θ - α) = cos(θ)cos(α) + sin(θ)sin(α) to find the solutions:
cos(θ - π/4) = cos(θ)cos(π/4) + sin(θ)sin(π/4) = (1/√2)cos(θ) + (1/√2)sin(θ)
Therefore, we have:
(1/√2)cos(θ) + (1/√2)sin(θ) = 2
Multiplying both sides by √2, we get:
cos(θ) + sin(θ)√2 = 2√2
Now we can use the identity cos(α) + sin(α) = √2 sin(α + π/4) to find the solutions:
cos(θ + π/4) = cos(θ)cos(π/4) - sin(θ)sin(π/4) = (1/√2)cos(θ) - (1/√2)sin(θ)
Therefore, we have:
(1/√2)cos(θ) - (1/√2)sin(θ) = 2√2
Multiplying both sides by √2, we get:
cos(θ) - sin(θ)√2 = 2
We now have two equations with two unknowns (cos(θ) and sin(θ)), which can be solved using algebraic methods. Adding the two equations together, we get:
2cos(θ) = 4√2
Dividing both sides by 2, we get:
cos(θ) = 2√2
Since the range of the cosine function is [-1,1], there are no real solutions to this equation. Therefore, there are no solutions to the original equation (cos θ)(cos θ) + 1 = (sin θ)(sin θ).
I believe this is helpful
Someone pls help . Thank you sm☄️ .

Answers
1) 3 is the Coefficient.
2) 10 is the constant.
3) 10.8 is the ans.
. a rancher has 60 m of fence and wishes to enclose a rectangular region. what is the maximum area that the 60 m can enclose? what are the dimensions of the maximal region? (a) write height as a fcn of base. height
Answers
The maximum area that the 60 m can enclose is 225m², the dimensions of the maximal region are 15m x 15m, and the height as an fcn of the base is 30 - b.
Let the base of the rectangular region be "b",
and the height be "h" and,
it is given that the perimeter of the rectangular region = 60m
(a) write height as an fcn of base
by using the formula of the perimeter of a rectangle,
2(h+b) = 60m
we can write, h = 30 - b
⇒Area of the rectangular region
area(A) = height × base
substituting the value of h.
= (30 - b) × b
thus, A(b)= 30b - b²
to find the maximum area that the 60 m can enclose
\(\frac{dA(b)}{db}\) should be equal to 0.
substituting the value of A(b).
30 - 2b = 0
thus, b = 15
maximum area = 30b - b²
substituting the value of b.
= (30 × 15) - 15²
thus, maximum area = 225m².
dimensions of the maximum region,
for maximum area height = base = 15m
thus, the dimensions of the maximum rectangular region are 15m x 15m.
know more about the area here: https://brainly.com/question/20693059
#SPJ4
let nn be the least positive integer that is both 2222 percent less than one integer and 1616 percent greater than another integer. find the remainder when nn is divided by 10001000.
Answers
The smallest integers k and m that satisfy this are k=1450 and m=975, so N = 1131.
How to solve word problems?
It's actually fairly easy to solve word problems using a tried-and-true step-by-step approach.
Aloud to yourself, read the issue.Make a Drawing.Ask yourself, "What am I looking for?"List the items that have been provided.Locate the key phrases.Solve.Verify your work.If N is 22 percent less than one integer k, then
N = 78/100 k
= 38k/100
In N is 16 percent greater than another integer m, So
N = 116m / 100
= 29m/25.
Therefore, k is divisible by 50 and m is divisible by 25.
Setting these two equal, we have 38k/100 = 29m/25.Multiplying by $50$ on both sides, we get 39k = 58m
Hence, The smallest integers k and m that satisfy this are k=1450 and m=975, so N = 1131.
To know more about word problems check the below link:
https://brainly.com/question/13818690
#SPJ4
What is i30
A. 1
B. -i
C. -1
D. i

Answers
In a process system with multiple processes, the cost of units completed in Department One is transferred to O A. overhead. O B. WIP in Department Two. ( C. Cost of Goods Sold. OD. Finished Goods Inventory.
Answers
In a process system with multiple processes, the cost of units completed in Department One is transferred to WIP (Work in Progress) in Department Two.
Here's a step-by-step explanation:
1. Department One completes units.
2. The cost of completed units in Department One is calculated.
3. This cost is then transferred to Department Two as Work in Progress (WIP).
4. Department Two will then continue working on these units and accumulate more costs.
5. Once completed, the total cost of units will be transferred further, either to Finished Goods Inventory or Cost of Goods Sold.
Remember, in a process system, the costs are transferred from one department to another as the units move through the production process.
To know more about cost of units refer here:
https://brainly.com/question/13873791
#SPJ11