S is the midpoint of RT. If RS = 6x + 2 and RT = 10x + 14, write the
equation you would use to solve for x.
Answers
Answer:
To solve for x, we set the two equations equal to each other
6x+2 = 10x+14 We will use inverse operations
2 = 4x+14.
-12 = 4x
x= -3
Related Questions
On average, five students from each high school class get full scholarships to four-year colleges. Assume that most high school classes have about 500 students. X = the number of students from a high school class that get full scholarships to four-year schools. Which of the following is the distribution of X?
P(5)
B(500, 5)
Exp(15)
N(5,(0.01)(0.99)500)
Answers
The notation B(500, 5) indicates that X follows a binomial distribution with n = 500 and p = 0.01.
What is binomial distribution?
The binomial distribution is a probability distribution that describes the number of successes in a fixed number of independent Bernoulli trials. It models situations where there are two possible outcomes, often referred to as "success" and "failure," and the probability of success remains constant for each trial.
The distribution of X, the number of students from a high school class that get full scholarships to four-year schools, would follow the binomial distribution with parameters n and p.
The correct distribution for X would be B(500, 5), where B represents the binomial distribution.
In this case, n = 500, which represents the number of trials (number of students in the high school class), and p = 5/500 = 0.01, which represents the probability of success (probability that a student gets a full scholarship).
The notation B(500, 5) indicates that X follows a binomial distribution with n = 500 and p = 0.01.
To know more about binomial distribution visit:
https://brainly.com/question/29163389
#SPJ4
On a separate piece of graph paper, graph y = Ixl - 1; then click on the graph until the correct one appears.



Answers
The function y = |x| - 1 is a translation of 1 unit downwards of the parent absolute value function, and its graph is the first one shown in the images.
How to graph the function?Here we want to graph:
y = |x| - 1
Notice that if we take the parent absolute value function:
y = |x|
And we translate it one unit downwards, we will get:
y = |x| - 1
Which is the function that we want to graph.
So to select the correct graph, we need to find the one that is the parent absolute value function translated one unit downwards. It is the one with the vertex at (-1, 0), which is the graph that appears on the first image.
If you want to learn more about absolute values:
https://brainly.com/question/3381225
#SPJ1
find the jacobian of the transformation x=3u, y=2uv and sketch the region g: 3<3u<6, 2<2uv<4
Answers
It is a rectangular region with u and v values ranging from 1 to 2.
To find the Jacobian of the transformation x = 3u, y = 2uv, we need to compute the partial derivatives ∂x/∂u, ∂x/∂v, ∂y/∂u, and ∂y/∂v.
Given:
x = 3u
y = 2uv
Calculating the partial derivatives:
∂x/∂u = 3
∂x/∂v = 0 (since x does not depend on v)
∂y/∂u = 2v
∂y/∂v = 2u
Now, we can construct the Jacobian matrix J:
J = [∂x/∂u ∂x/∂v]
[∂y/∂u ∂y/∂v]
Substituting the partial derivatives we calculated earlier:
J = [3 0]
[2v 2u]
Therefore, the Jacobian of the transformation is:
J = [3 0]
[2v 2u]
To sketch the region described by the inequalities g: 3 < 3u < 6, 2 < 2uv < 4, we can consider the ranges of u and v that satisfy these conditions.
From the inequality 3 < 3u < 6, we have:
1 < u < 2
From the inequality 2 < 2uv < 4, we can divide both sides by 2:
1 < uv < 2
Since u and v must both be greater than 1, we can determine the range of v:
1 < v < 2
Now, we can sketch the region in the u-v plane bounded by the conditions:
1 < u < 2
1 < v < 2
It is a rectangular region with u and v values ranging from 1 to 2.
To know more about Jacobian of the Transformation related question visit:
https://brainly.com/question/32527264
#SPJ11
how do you convert fractions to decimals?
Answers
Answer:
divide the fractions
Step-by-step explanation:
lets say we have 23/5
we can divide 23 by 5 and get a decimal of 4.6
or lets say we got 1/5
divide 1 by 5 and you will get 0.2
RIGHT ANSWER GETS BRAINLIEST AND 30 POINTS

Answers
Answer:
y=(4/5)x
Step-by-step explanation:

Solve for the missing side

Answers
Step-by-step explanation:
12²=a²+9²
144=a²+81
a²=144-81
a²=63
a=√63
a=7.94
uppose , i.e. has a t-distribution with 10 degrees of freedom. What proportion of this t-distribution falls within and
Answers
95% of the t-distribution with 10 degrees of freedom falls within the interval from -2.228 to 2.228.
To answer this question, we need to use the t-distribution table or a statistical software that can calculate t-distribution probabilities.
Assuming you meant to specify the interval between -2.228 and 2.228, which is the 95% confidence interval for a two-tailed test with 10 degrees of freedom, we can use the t-distribution table to find the proportion of the t-distribution that falls within this interval. Alternatively, we can use a statistical software to calculate this proportion directly.
Using the t-distribution table, we can find the cumulative probability for t = -2.228 and t = 2.228 with 10 degrees of freedom. The cumulative probability for t = -2.228 is 0.025, and the cumulative probability for t = 2.228 is 0.975. Therefore, the proportion of the t-distribution that falls within the interval from -2.228 to 2.228 is:
0.975 - 0.025 = 0.95
This means that 95% of the t-distribution with 10 degrees of freedom falls within the interval from -2.228 to 2.228.
Alternatively, we can use a statistical software, such as R or Python, to calculate the same probability. For example, in R, we can use the pt() function to calculate the cumulative probability for a given t-value and degrees of freedom. The code would look like:
pt(2.228, df = 10) - pt(-2.228, df = 10)
This would give us the same result of 0.95.
Learn more about "t-distribution" : https://brainly.com/question/17469144
#SPJ11
Which graph represents a function with a domain of all numbers greater than or equal to -7 and less than 2? Your explanation should include all information about reading domain on a graph given the limitations. As well as how the different circles affects the notation on the graph when equal to and not equal to are used.
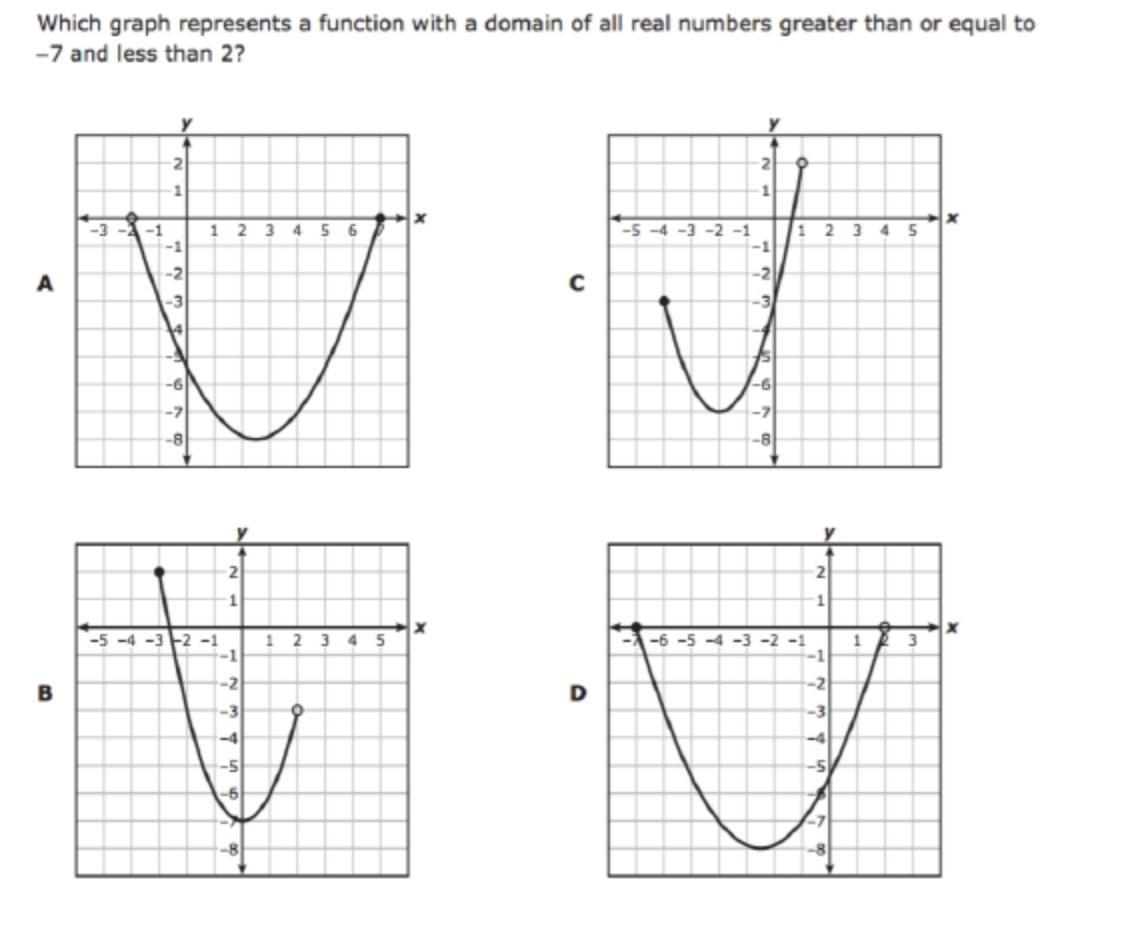
Answers
Answer: D.
Step-by-step explanation:
The way to know if it is “greater than or equal to” opposed to jsut greater than is to look at the dot. If it is filled in it is “equal to” if not it isn’t.
Josh has been working andsaving money in order to buy a car andtravel the country. According to hiscalculations, it will cost him $1450 amonth for all his expenses. If Josh hassaved up $40,000, and will be purchasinga car for $16,500, at most, how manymonths will he have enough money totravel?
Answers
Answer:
16 months
Step-by-step explanation:
40k-16.5k=23.5k. 23.5k/1450= A little bit more than 16 months.
Study the food web below and answer the following :
i. In the pyramid of numbers there is an increase in numbers towards the base. Mention a pyramid where the base will be smaller.
ii. Predict the impact of removing snakes from this food web

Answers
Answer:
predict the impact of removing snakes from this food web
The fastest speed recorded forerunner 27 mph. This is 20% of the fastest speed for a water skier find the record for a water skier.
Answers
Answer: 135
Step-by-step explanation: We know that the forerunner is 1/5 the speed of the water skier as 20/100 is 1/5. Now if we "reverse" this we can multiply 27 by 5 to find the speed of the water skier, this is 135 which is the speed of the water skier. Hope this helped :)
Solve each system
7) 8x-y=3
y=-8x - 3
Please help
Answers
Answer:
i cant answer this because of my school computer but its simple
Step-by-step explanation:
Answer: x & y
0 & -3
1 & 5
slope : 8
y intercept : -3
In 2016, George Washington's birthday fell on Friday, February 12. On what day of the week does Lincoln's birthday fall in 2025?
Need solution thanks
Answers
Wednesday
If you use a calender, it falls on a wednasday
53% of 2343 american adults surveyed said, they have watched digitally streamed tv programming on some type of device. what sample size would be required for the width of a 99% ci to be at most 0.05 irrespective of the value of at 99%
Answers
The sample size that would be required for the width of 99% is 2653.
What is sample size?The number of subjects involved in a sample size is referred to as the sample size in market research. A set of people chosen from the general community who are thought to be a representative sample size for that particular study is referred to as the sample size.
The following details are given:
Margin of error, E = 0.025; Significance Level, = 0.01
The proportion p is estimated to be p = 0.53.
The significance level with a critical value of 0.01 is 2.58.
The smallest sample size needed to estimate the population proportion p within the necessary margin of error is determined using the formula shown below:
n >= p*(1-p)*(zc/E)2 n = 0.53 *(1 - 0.53*)2 n = 2652.97 *(1-p)*(2.58/0.025)2
As a result, we determine that n = 2653 is the minimal sample size needed to satisfy the criteria that
n >= 2652.97 and that it must be an integer value.
Sample size is 2653.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ4
I will mark you brainlist im begging please help me
In order to keep the Bermuda Triangle on the Flat Earth from toppling over, it was balanced on the hole which leads to the interior of the hollow Earth. If the vertices of the Bermuda Triangle are given by (1,3) , (2,7) , and (6,2). In order to find the hole we will need to find the intersection of at least 2 lines. Name 2 points through which one of those lines will pass (in the form (x,y),(x,y))
Answers
The slope-intercept representation of a linear function is given by the rule shown as follows:
y = mx + b
The coefficients of the function, along with their meaning, are listed as follows:
m is the slope, representing the rate of change of y relative to x.b is the y-intercept of the function, which is the value of y when x = 0.Given two points, only one line will pass through them.
Using a calculator, the lines are given as follows:
Points (1,3) and (2,7): y = 4x - 1.Points (2,7) and (6,2): y = -1.25x + 10.5.Then the x-coordinate of the point in which the lines intersect is obtained as follows:
4x - 1 = -1.25x + 10.5
5.25x = 11.5
x = 2.19.
The y-coordinate can be found in any of the equations, hence:
y = 4(2.19) - 1 = 7.76.
Another point on the line y = 4x - 1 has a x-coordinate of 3 and an y-coordinate obtained as follows:
y = 4(3) - 1 = 12 - 1 = 11.
A similar problem, also featuring linear functions, is given at https://brainly.com/question/24808124
#SPJ1
Adrian drove 60 miles in 1.2 hours. Vincent drove 175 miles in 2.5 hours. If the
speed limit is 40 miles per hour, who was speeding over 40 miles per hour?
O Adrian
O Both are going over (speeding)
O Both are going under
Vincent
Answers
Answer:
Both are going over the speed limit
Step-by-step explanation:
divide 60 by 1.2 to get 50 miles an hour
Divide 175 by 2.5 to get 70 miles an hour
They both are going over 70 miles an hour
Hopes this helps please mark brainliest
Potential Energy can be described as Ep= m.g.h where m = mass which is measured in kilograms, g = acceleration of gravity which is measured in meters per second (m/s2), and h = height which is measured in meters . What is a possible unit measure for Potential Energy
Answers
We need to analyze the units of each of the magnitudes and solve the operations between them:
\(\begin{gathered} m\to kg \\ g\to\frac{m}{s^2} \\ h\to m \\ m\cdot g\cdot h\to kg\cdot\frac{m}{s^2}\cdot m=kg\cdot\frac{m^2}{s^2} \end{gathered}\)A possible unit for potential energy is kg*m^2/s^2.
Also we can use distributive property to replace some of the units by derived units, for example, Newtons:
\(undefined\)Identifying Types Of Angles: Check all relationships between angle 1 and angle 2.
Am I doing this right?

Answers
#1. Vertical
#2. Adjacent, Complementary
#3. Adjacent, Linear Pair, Supplementary
---A linear pair forms a line, which is equal to 180 degrees
#4. Adjacent
#5. Vertical, Complementary
#6. Vertical, Supplementary
---There is a 90 degree angle within this problem. If one angle is 90 degrees, then they are all 90 degrees, which makes the sum of angle 1 and 2 = 180. So, they are supplementary.
Hope this helps!
The relationship between angle 1 and 2 are as follows:
1. ∠1 ≅ ∠2 (vertical angles)
2. ∠1 and ∠2 are adjacent and complementary angles.
3. ∠1 and ∠2 are linear pairs and supplementary angles
4. ∠1 and ∠2 are adjacent angles
5. ∠1 and ∠2 are vertical angles
6. ∠1 and ∠2 are vertical angles and supplementary angles.
1.
Vertical angles:Vertical angles that are pair of opposite angles formed by intersecting lines. Vertical angles share the same vertex.Therefore,
∠1 ≅ 2 (vertical angles)
2.
Adjacent angles:Adjacent angles have common sides and common vertexComplementary angle :This angles sum up to 90 degrees.Therefore,
∠1 and ∠2 are adjacent and complementary angles.
3.
Linear pair angles:This is a pair of adjacent angles form when two lines intersect. It sum up to 180 degrees. Supplementary angles:Supplementary angles are angles that sum up to 180 degrees.∠1 and ∠2 are linear pairs and supplementary angles.
4.
∠1 and ∠2 are adjacent angles
5.
∠1 and ∠2 are vertical angles
6.
∠1 and ∠2 are vertical angles and supplementary angles
learn more on angles here: https://brainly.com/question/18166236?referrer=searchResults
Pls answer this correctly
The number of pieces of popcorn in a large movie theatre popcorn bucket is normally distributed, with a mean of 1720 and a standard deviation of 20. Approximately what percentage of buckets contain between 1680 and 1760 pieces of popcorn?
Approximately 68%
Approximately 75%
Approximately 95%
99.7%
Answers
an event that increases the probability that a response will be repeated is called _____.
Answers
The term that describes an event that increases the likelihood of a response being repeated is known as reinforcement.
Reinforcement can be defined as any consequence that strengthens or increases the probability of a behavior occurring again in the future. This can include positive reinforcement, which involves adding a desirable consequence after a behavior, or negative reinforcement, which involves removing an aversive consequence after a behavior. Both types of reinforcement have been shown to be effective in increasing the likelihood of a behavior being repeated.
Overall, understanding the concept of reinforcement is essential in the field of psychology, particularly in the areas of behaviorism and behavior modification. By providing positive consequences after desired behaviors, individuals can be motivated to continue engaging in those behaviors, which can lead to long-term positive changes. Reinforcement can also be used to shape new behaviors or replace unwanted behaviors with more desirable ones.
To know more about positive changes visit:-
https://brainly.com/question/15411632
#SPJ11
A pipefitter must connect two pipes as shown. The run is 32 feet while the set is 21 feet. How long a pipe will he need, and what will be the connecting angles? Round tothe nearest hundredth.

Answers
In order to determine how long the pipe connector must be, we can use the Pythagorean Theorem.
\(c^2=a^2+b^2\)where "a" and "b" are either run or set in the diagram while "c" is the length of the pipe.
Let's say "a" is run which is 32 ft and "b" is the set which is 21 ft. Let's plug this into the formula above.
\(c^2=32^2+21^2\)Then, solve for c.
\(\begin{gathered} c^2=1024+441 \\ c^2=1465 \end{gathered}\)Get the square root on both sides of the equation.
\(\sqrt{c^2}=\sqrt{1465}\Rightarrow c=38.275\approx38.28ft\)Hence, the pipe connector must be 38.28 ft.
To determine the angle, we can use either the cosine or sine functions.
For angle "a", we can use the sine function and we use the set and the length of the pipe connector.
\(\theta=sin^{-1}\frac{21}{\sqrt{1465}}\)Using the calculator, the value of angle theta is:
\(\theta=33.274\approx33.27\degree\)The measure of angle "a" is approximately 33.27°.
For angle "b", we can use the sine function and we use the run and the length of the pipe connector.
\(\theta=sin^{-1}\frac{32}{\sqrt{1465}}\)\(\theta=56.725\approx56.73\degree\)The measure of angle "b" is approximately 56.73°.
Answer:
See below
Step-by-step explanation:
Run and rise and x form a right triangle ...use pythag theorem
x^2 = 32^2 + 21^2 shows x = 38.28 ft
Right triangle tan (angle ) = opposite leg / adjacent leg
angle a = arctan ( 21/32) = 33.27° angle b = arctan (32/21) = 56.73°
is y=5^w an exponential function if so state the initial value and the base if not then which type of function is it
Answers
By using the property of exponential function, the results obtained are
Base of the function is 5.
Initial value of the function is close to zero.
What are exponent?
Exponent tells us how many times a number is multiplied by itself.
For example : In \(2^4 = 2\times 2\times 2\times 2\)
Here, 2 is multiplied by itself 4 times.
If \(a^m = a \times a\times a....\times a\) (m times), a is the base and m is the index.
Here,
\(y = 5^w\) is an exponential function.
The base of the function is 5.
As \(x \rightarrow -\infty\), the function tends to 0
So the initial value of the function is close to zero.
To learn more about exponent, refer to the link:
https://brainly.com/question/11975096
#SPJ1
2|x - 3| - 5 = 7
“solve the equation”
Answers
Answer:
Combine solutions: x=-3 or x=9
Step-by-step explanation:
Answer:
x = - 3, x = 9
Step-by-step explanation:
Given
2| x - 3 | - 5 = 7 ( add 5 to both sides )
2|x - 3 | = 12 ( divide both sides by 2 )
| x - 3 | = 6
The absolute value function always gives a positive value, however, the expression inside the bars can be positive or negative, that is
x - 3 = 6 or - (x - 3) = 6
Solving both equations
x - 3 = 6 ( add 3 to both sides )
x = 9
or
- (x - 3) = 6
- x + 3 = 6 ( subtract 3 from both sides )
- x = 3 ( multiply both sides by - 1 )
x = - 3
As a check
2|9 - 3| - 5 = 2|6| - 5 = 12 - 5 = 7 ← Correct
or
2|- 3 - 3| - 5 = 2|- 6| - 5 = 2 |6| - 5 = 12 - 5 = 7 ← Correct
Thus the solutions are x = - 3, x = 9
There was 1/3 of a box of cereal left. Four brothers shared it evenly how much cereal did they all get
Answers
Answer:
1/12
Step-by-step explanation:
1/3 divided by 4
keep it change it flip it
would change to 1/3 times 1/4 = 1/12
hope this helps!
the probability that an individual randomly selected from a particular population has a certain disease is .05. a diagnostic test correctly detects the presence of the disease 98% of the time and correctly detects the absence of the disease 99% of the time. if the test is applied twice, the two test results are independent, and both are positive, what is the (posterior) probability that the selected individual has the disease
Answers
The (posterior) probability that the selected individual has the disease, given two positive test results, is approximately 66.04%.
To determine the posterior probability that the individual has the disease, we can use Bayes' theorem. Let's denote the following probabilities:
- P(D) as the probability of the disease (0.05 in this case),
- P(D') as the probability of not having the disease (1 - P(D)),
- P(Pos|D) as the probability of testing positive given that the individual has the disease (0.98),
- P(Neg|D) as the probability of testing negative given that the individual has the disease (1 - P(Pos|D)),
- P(Pos|D') as the probability of testing positive given that the individual does not have the disease (1 - specificity, which is 1 - 0.99 = 0.01),
- P(Neg|D') as the probability of testing negative given that the individual does not have the disease (specificity, which is 0.99).
To calculate the posterior probability, P(D|Pos1, Pos2), applying Bayes' theorem:
P(D|Pos1, Pos2) = (P(Pos1, Pos2|D) * P(D)) / P(Pos1, Pos2),
where P(Pos1, Pos2|D) is the probability of observing two positive test results given the individual has the disease.
Since the two test results are independent, we can calculate P(Pos1, Pos2|D) as the product of the individual probabilities: P(Pos|D) * P(Pos|D) = 0.98 * 0.98 = 0.9604.
Now, we need to calculate the denominator, P(Pos1, Pos2), which represents the probability of observing two positive test results, regardless of whether the individual has the disease or not.
P(Pos1, Pos2) = P(Pos1, Pos2|D) * P(D) + P(Pos1, Pos2|D') * P(D').
Since the two tests are independent, we can calculate P(Pos1, Pos2|D') as the product of the individual probabilities: P(Pos|D') * P(Pos|D') = 0.01 * 0.01 = 0.0001.
Using these values, we can calculate the denominator as:
P(Pos1, Pos2) = (0.9604 * 0.05) + (0.0001 * 0.95) = 0.04802 + 0.000095 = 0.048115.
Finally, substituting the values into the Bayes' theorem equation:
P(D|Pos1, Pos2) = (0.9604 * 0.05) / 0.048115 ≈ 0.6604.
Therefore, the (posterior) probability that the selected individual has the disease, given two positive test results, is approximately 66.04%.
To learn more about denominator click here: brainly.com/question/32621096
#SPJ11
a candle maker sells sets of candles in the shape of square pyramids. the volume of a smaller candle is 125 cubic centimeters. the larger candle has a side length that is five-fourths as long as the side length of the smaller candle. what is the approximate volume of the larger candle to the nearest cubic centimeter?
Answers
The approximate volume of the larger candle is 244 cubic centimeters.
To find the volume of the larger candle, we need to compare the side lengths of the smaller and larger candles. Let's denote the side length of the smaller candle as "s."
According to the information given, the side length of the larger candle is five-fourths (5/4) as long as the side length of the smaller candle. Therefore, the side length of the larger candle can be calculated as (5/4) * s.
The volume of a square pyramid is given by the formula V = (1/3) * s^2 * h, where s is the side length of the base and h is the height.
Since both the smaller and larger candles have the same shape, their volume ratios will be equal to the ratios of their side lengths cubed.
Let's substitute the values into the volume ratio equation:
(125 / V_larger) = (s_larger / s_smaller)^3
Given that V_smaller = 125 cubic centimeters, we can rewrite the equation as:
(125 / V_larger) = ((5/4) * s_smaller / s_smaller)^3
Simplifying the equation:
(125 / V_larger) = (5/4)^3
Calculating (5/4)^3:
(125 / V_larger) = (125 / 64)
Cross-multiplying the equation:
125 * 64 = V_larger * 125
Solving for V_larger:
V_larger = (125 * 64) / 125
Approximating the value:
V_larger ≈ 64 cubic centimeters
The approximate volume of the larger candle is 244 cubic centimeters, rounded to the nearest cubic centimeter
To know more about volume visit:
https://brainly.com/question/27710307
#SPJ11
what number is that which if increased by 20 of itself equals 48
Answers
Answer:
28
Step-by-step explanation:
let the number be n then increased by 20 = n + 20 and
n + 20 = 48 ( subtract 20 from both sides )
n = 28
Ramone pays $6 for lunch and $2 for juice each day.
Which ordered pair represents how much Ramone spends in 20 days for lunch and juice?
A.
(6, 2)
B.
(26, 22)
C.
(120, 22)
D.
(120, 40)
Answers
Answer:
D
Step-by-step explanation:
If you were trying to find the amount of money that he would pay in 20 days, you would need to multiply the lunch and juice money by the amount of days.
6($) x 20(days) = 120
2 ($)x 20(days) = 40
So it would be 120, 40
=Answer choice D.
Grady is comparing three investment accounts offering different rates.
account a: apr of 4.95% compounding monthly
account b: apr of 4.85% compounding quarterly
account c: apr of 4.75% compounding daily which account will give grady at least a 5% annual yield? (4 points)
group of answer choices
account a
account b
account c
account b and account c
Answers
From comparing three investment accounts offering different rates, Account A will give Grady at least a 5% annual yield. Therefore, the correct option is option 1.
To determine which investment account will give Grady at least a 5% annual yield, we will need to calculate the Annual Percentage Yield (APY) for each account and compare them. Here are the given terms for each account:
Account A: APR of 4.95%, compounding monthly
Account B: APR of 4.85%, compounding quarterly
Account C: APR of 4.75%, compounding daily
1: Use the APY formula:
APY = (1 + r/n)^(nt) - 1
where r is the annual interest rate (as a decimal), n is the number of compounding periods per year, and t is the number of years.
2: Calculate APY for each account.
Account A:
APY = (1 + 0.0495/12)^(12*1) - 1
APY ≈ 0.0507 or 5.07%
Account B:
APY = (1 + 0.0485/4)^(4*1) - 1
APY ≈ 0.0495 or 4.95%
Account C:
APY = (1 + 0.0475/365)^(365*1) - 1
APY ≈ 0.0493 or 4.93%
3: Compare the APYs to determine which account(s) meet the 5% annual yield requirement.
Based on the calculations, Account A has an APY of 5.07%, which is greater than the 5% annual yield requirement. Therefore, Account A will give Grady at least a 5% annual yield.
Learn more about Annual Percentage Yield:
https://brainly.com/question/27997520
#SPJ11
X\(\sqrt{x}\) + 7x + 10
factor the equation
algebra 2
Answers
There is no real solution for the equation X√x + 7x + 10.
A number or other mathematical object is factorized or factored when it is written as the product of numerous factors, typically smaller or simpler things of the same kind. For instance, factorizing the number 15 as 3 5
Solve X√x + 7x + 10 for x.
Subtract 7x from both sides
X√x + 7x + 10 - 7x = -7x
X√x + 10 = -7x
Subtract 10 from both sides
X√x + 10 - 10 = -7x - 10
X√x = -7x - 10
Divide both sides by √x
X√x / √x = (-7x - 10) / √x
x = (-7x - 10) / √x
The defined range
(0 , ∝)
Hence, The equation Xx + 7x + 10 has no actual solution.
To learn more about Factor
https://brainly.com/question/25829061
#SPJ1