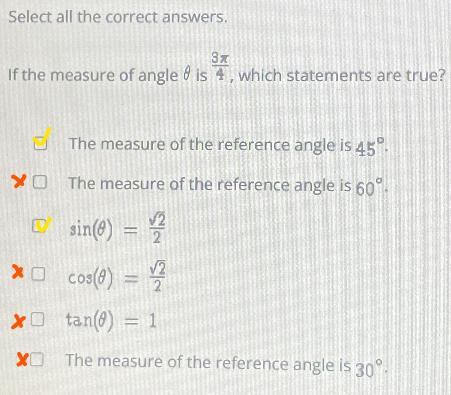
Select all the correct answers.3xIf the measure of angle 8 is , which statements are true?The measure of the reference angle is 45°The measure of the reference angle is 60°.sin() = 2V2o cos(0) = 12tan(0) = 1The measure of the reference angle is 30°-
Answers
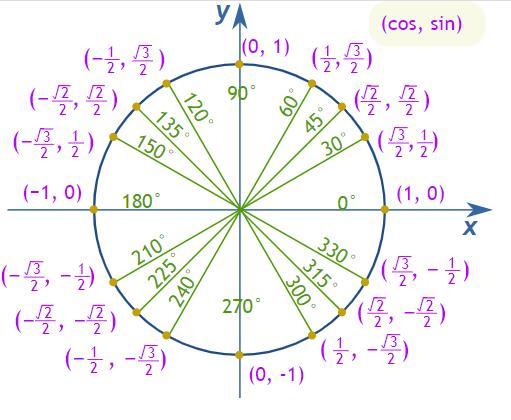
Answer with Explanation: The provided angle theta is:
\(\theta=\frac{3}{4}\pi r=135^{\circ}\)According to the unit circle, we have the following:
Therefore the (1) sin(theta) , (2) cos(theta) and (3) tan(theta) are as follows:
(1)
\(\begin{gathered} sin(\theta)=\frac{\text{ Opposite}}{\text{ Hypotenuse}} \\ sin(\theta)=\frac{\sqrt{2}}{2}\div1=\frac{\sqrt{2}}{2} \\ sin(\theta)=\frac{\sqrt{2}}{2} \end{gathered}\)(2)
\(\begin{gathered} cos(\theta)=\frac{\text{ Adjacent}}{\text{ Hypotenuse}}=-\frac{\sqrt{2}}{2}\div1=-\frac{\sqrt{2}}{2} \\ cos(\theta)=-\frac{\sqrt{2}}{2} \end{gathered}\)(3)
\(\begin{gathered} tan(\theta)=\frac{\text{ Opposite}}{\text{ Adjacent}}=\frac{\sqrt{2}}{2}\div-\frac{\sqrt{2}}{2}=-1 \\ tan(\theta)=-1 \end{gathered}\)The measure of the refrence angle is:
\(\theta_r=180^{\circ}-135^{\circ}=45^{\circ}\)In conclusion, therefore the only true statements are as follows:
Related Questions
A puppy and a kitten are 180 feet apart when they see each other. The puppy can run at a speed of 25 feet per second, while the kitten can run at a speed of 20 feet per second.
How long will it take the kitten to catch up to the puppy if the puppy runs away from the kitten, and the kitten simultaneously starts chasing the puppy?
Answers
Answer:
an infinitely long time
Step-by-step explanation:
You want to know the time it takes for a kitten running 20 ft/s to catch a puppy running 25 ft/s when they start 180 ft apart and the puppy runs away from the kitten.
NeverThe kitten runs slower than the puppy, so can never catch up to it.
<95141404393>
Consider the function f(x)=2x−−√−8. If f−1(x) is the inverse function of f(x), find f−1(2)
Answers
\(f^(-1)(2) = 6\), which is consistent with our earlier result.
What is inverse function?A function that "undoes" another function is known as an inverse function. If f(x) is a function, then f(x inverse, )'s indicated by f-1(x), is a function that accepts f(x output )'s as an input and outputs f(x initial )'s input.
Given the function f(x) = √(2x - 8), if f^(-1)(x) is the inverse function of f(x), what is \(f^(-1)(2)\)?
Solution:
To find f^(-1)(2), we need to find the value of x such that \(f(x) = 2\) . We can set up an equation:
\(f(x) = \sqrt(2x - 8) = 2\)
Squaring both sides, we get:
\(2x - 8 = 4\)
\(2x = 12\)
\(x = 6\)
Therefore, \(f^(-1)(2) = 6.\)
We can also verify this result by using the definition of an inverse function. If f^(-1)(x) is the inverse function of f(x), then by definition:
\(f(f^(-1)(x)) = x\)
We can substitute x = 2 and solve for f^(-1)(2):
\(f(f^(-1)(2)) = 2\)
\(f^(-1)(2) = (f(6))^(-1)\)
f(6) = √(2(6) - 8) = √4 = 2
Therefore,\(f^(-1)(2) = 6\), which is consistent with our earlier result.
Learn more about function here:
https://brainly.com/question/2541698
#SPJ1
Select the correct answer from each drop-down menu.
What type of risk applies to an investment in Treasury bonds?
The risk that the value of the Treasury bond will diminish over time if the value of the dollar decreases, or buys less than it used to, is called
risk. Treasury bonds are seen to have no
risk because they're backed by the promise of the US government
to repay the bond.
Answers
Answer:
1. Inflationary
2. Credit
Step-by-step explanation:
The risk that the value of the Treasury bond will diminish over time if the value of the dollar decreases, or buys less than it used to, is called inflationary risk. Treasury bonds are seen to have no credit risk because they're backed by the promise of the US government to repay the bond.
5 = -8 + c
i need help this is extra credit
Answers
Answer:
c is equal to 13
because -8 + 8 is 0 and 0 + 5 is 5 and 8 + 5 is 13
The combined SAT scores for the students at a local high school are normally distributed with a mean of 1527 and a standard deviation of 295. The local college includes a minimum score of 1380 in its admission requirements. What percentage of students from this school earn scores that satisfy the admission requirement
Answers
Answer:
69.15% of students from this school earn scores that satisfy the admission requirement.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean of 1527 and a standard deviation of 295.
This means that \(\mu = 1527, \sigma = 295\)
The local college includes a minimum score of 1380 in its admission requirements. What percentage of students from this school earn scores that satisfy the admission requirement?
The proportion is 1 subtracted by the pvalue of Z when X = 1380. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{1380 - 1527}{295}\)
\(Z = -0.5\)
\(Z = -0.5\) has a pvalue of 0.3085
1 - 0.3085 = 0.6915
0.6915*100% = 69.15%
69.15% of students from this school earn scores that satisfy the admission requirement.
"A number n equals 7 more than half the number"
Answers
The number 'n' is equal to 14
In the question, we have been given that the number n is equal to 7 more than half of the number 'n'.
So in these linear equation-solving types of problems, first of all, we convert the written sentence into an equation.
So the equation for the following problem statement is -
n = 7 + n/2
{since we have been given the number equals 7 more than half of the number }
Solving the equation we have,
n = 14.
We can easily see that 14 is the number which is 7 more than half of itself.
Know more about linear equation solving at - https://brainly.com/question/25858757
15 Paid FTEs and have a department non-productive rate of 10%, how many productive FTEs does the department have?
Answers
Answer:
I'm sorry but I don't know but I have a question
Step-by-step explanation:
how do you post questions on the brainly app??
Answer:
15x40 = 600 x10% =60
Step-by-step explanation:
15 Paid FTEs and have a department non-productive rate of 10%, how many productive FTEs does the department have?
What’s the answer to number 1?

Answers
Answer:
increase = New number - original number
inc % = (increase ÷ original number) *100%
Step-by-step explanation:
133 - 76 = 56
inc % = 57 ÷ 76 = 0.75
0.75*100% = 75%
.
evaluate 16^-3/4
Evaluation of the exponents
Answers
Answer:
I think it is -12
Multiply -0.75 (3 quarters) by 16.
The negative cancels out the positive number.
Since the exponent is not saying multiply the number by itself a number of times, we could make a hypothesis that this is just multiplication.
Normally, this ↑ is not the case, but here, I could make an exception.
I hope this helps you, let me know if you need something else.
2. Ashton is x years old. Bentley is 2 years older than Ashton. Three times Bentley’s age is equal to 18. The purpose of this exercise is to check your understanding on setting up equations and showing the steps to solving a simple equation. (c) Use the information above to set up another equation or expression and solve to show old Bentley is.
thank you!
Answers
Answer:
the awnser is that Bently is 6 And Ashton is 4
Step-by-step explanation:
the reason I get this awnser is because it says that bently is 2 years older than Ashton and 3 times so you think what can be times 3 so the first awnser i got was 6 because 6 times 3 equals 18 so then I subtracted 2 from that to create the number of 6 for Bentley and 4 for Ashton
BRAINLIEST PLEASEfind area and perimeter

Answers
Answer: The simplest (and most commonly used) area calculations are for squares and rectangles. To find the area of a rectangle, multiply its height by its width. For a square you only need to find the length of one of the sides (as each side is the same length) and then multiply this by itself to find the area.
Step-by-step explanation:
I WILL givee brainliesttt

Answers
explanation: t
What is an example of "A one-to-one function of P onto Q is an isomorphism of P and Q "?

Answers
An example of a one-to-one function that is an isomorphism between sets P and Q is the function f: P -> Q defined as f(x) = 2x, where P and Q are the sets of integers.
How to Identify a One-to-One Function?An example of a one-to-one function that is an isomorphism between sets P and Q is the function f: P -> Q defined as f(x) = 2x, where P and Q are the sets of integers.
This function is one-to-one because for every element x in P, there is a unique element 2x in Q. It is onto because every element y in Q has a preimage x in P such that f(x) = y (e.g., y/2 = x).
Furthermore, this function preserves the group structure between P and Q, as it satisfies the properties of an isomorphism. In this case, the group structure is addition, and the function f preserves addition: f(x + y) = 2(x + y) = 2x + 2y = f(x) + f(y) for all x, y in P.
Therefore, the function f: P -> Q defined as f(x) = 2x is an example of a one-to-one function that is an isomorphism between sets P and Q.
Read more about One-to-One Function at: https://brainly.com/question/30563810
#SPJ1
answer needed
pls help me

Answers
Answer:
26
Step-by-step explanation:
The sector of a circle has an area of 104pi/9
square inches and a central angle with measure 65 degree
. What is the radius of the circle, in inches?
Answers
Answer:
Given:
Area of the sector (A) = 104π/9 square inches
Central angle (θ) = 65 degrees
The formula for the area of a sector of a circle is:
A = (θ/360) * π * r^2
We can rearrange this formula to solve for the radius (r):
r^2 = (A * 360) / (θ * π)
Plugging in the given values:
r^2 = (104π/9 * 360) / (65 * π)
r^2 = (104 * 40) / 9
r^2 = 4160 / 9
r^2 ≈ 462.22
Taking the square root of both sides:
r ≈ √462.22
r ≈ 21.49
Therefore, the radius of the circle is approximately 21.49 inches.
Answer: 8 inches
Step-by-step explanation:
Which is equivalent to x(-14x + 9)? A) -28x + 9 B) -14x2 + 9 C) -14x2 + 9x D) -28x2 + 9x
Answers
Answer:
By distributive property, we get
a (b + c) = ab + ac\( \longmapsto x( - 14x + 9) \\ = \boxed{ - 14 {x}^{2} + 9x}✓\)
C) -14x² + 9x is the right answer.Plz help me well mark brainliest if you are correct!.....

Answers
Answer:
The first one is the answer to the question
On the map, , the distance is represented by a scale of 1:5000. If the distance between two buildings is shown as 3 cm on the map, then what is the actual distance between the two buildings in meter?
HELP ME PLEASE!!!!!!!!!!
Anyways, I can only offer 10 points!
Answers
The total distance between the buildings is 150 meters. In the event a map placed one is to 5000 scales then it projects one unit on the map represents 5000 units in the actual world.
We can apply this ratio to alter the distance on the map to the actual distance between the buildings or objects in the given case that the distance is shown as 3 centimeters then the actual distance in meters is followed 1 centimeter on the map represents 5000 centimeters in the real world.
1 cm on the map = 5000 cm in the actual world
3 cm on the map = (3 x 5000) cm in the actual world
= 15000 cm in the actual world
To alter cm to meters, we need to can apply division by 100 since there are 100 cm in a meter. So, the actual distance between the two buildings is:
15000 cm / 100 = 150 meters
The real distance between the two buildings is 150 meters.
To learn more about the division
https://brainly.com/question/30126004
#SPJ1
Graph the line with slope 1/3 and y-intercept −2.
Answers
The graph of the function y = 1/3x - 2 is added as an attachment
Sketching the graph of the functionFrom the question, we have the following parameters that can be used in our computation:
Slope = 1/3y-intercept = -2So, the equation is
y = 1/3x - 2
The above function is a linear function that has been transformed as follows
Vertically stretched by a factor of 1/3Shifted down by 2 unitsNext, we plot the graph using a graphing tool by taking note of the above transformations rules
The graph of the function is added as an attachment
Read more about functions at
brainly.com/question/2456547
#SPJ1

Answer
-10 – (-2) =
Answers
Answer:
8
Step-by-step explanation:
- (-2) is the same as + 2
-10 + 2 = -8
Answer:
-8
Step-by-step explanation:
Since there are two minus sign with the two, make it into plus. There fore the equation is -10+2= -8!
A school trip needs at least one adult to every six students. The coach holds a maximum of 52 passengers. What is the maximum number of students that can go on the trip?
Answers
In linear equations, 49 is the maximum number of students that can go on the trip.
What are instances of linear equations?
A linear equation with one variable is one that contains just one variable. It has the formula Ax + B = 0, with A and B being any two real numbers and x being an ambiguous variable with only one possible value. One such linear equation in one variable is 9x + 78 = 18.If total passengers are 52 then,
42 because 6 * 7 = 42 and
42 + 7 = 49
Learn more about linear equations
brainly.com/question/11897796
#SPJ9
Which equation represents a line which is perpendicular to the line y=-5/4x-4?A. 4y−5x=−4B. 5x+4y=−8C. 4x−5y=15D.4x+5y=40
Answers
The slope of a line, m, comes in the equation as the coefficient of x.
In the given equation, m= -5/4. Two perpendicular lines have slopes that are the negative reciprocals of each other.
So, the slope of the perpendicular line will be +4/5.
Between the given options, letter c will be:
4x-5y=15
-5y=15-4x (divided by -5)
y=4/5x-3
Letter C
-1000 2/3 is not real fraction. True or false
Answers
True, While "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
The statement "-1000 2/3 is not a real fraction" is true. A real fraction is a mathematical expression that represents a ratio of two real numbers. In a fraction, the numerator and denominator are both real numbers, and they can be positive, negative, or zero.
In the given statement, "-1000 2/3" is not a valid representation of a fraction. The presence of a space between "-1000" and "2/3" suggests that they are separate entities rather than being part of a single fraction.
To represent a mixed number (a whole number combined with a fraction), a space or a plus sign is typically used between the whole number and the fraction. For example, a valid representation of a mixed number would be "-1000 2/3" or "-1000 + 2/3". However, without the proper formatting, "-1000 2/3" is not considered a real fraction.
It's important to note that "-1000 2/3" can still be expressed as an improper fraction. To convert it into an improper fraction, we multiply the whole number (-1000) by the denominator of the fraction (3) and add the numerator (2). The result would be (-1000 * 3 + 2) / 3 = (-3000 + 2) / 3 = -2998/3.
In conclusion, while "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
for more such question on fraction visit
https://brainly.com/question/30122573
#SPJ8
7. From the observation deck of a skyscraper, Matthew
measures a 45° angle of depression to a ship in the harbor
below. If the observation deck is 1053 feet high, what is
the horizontal distance from the base of the skyscraper out
to the ship? Round your answer to the nearest tenth of a
foot if necessary.
Answers
The horizontal distance from the base of the skyscraper out to the ship would be 1053 feet.
What are the trigonometric ratios?Trigonometric ratios for a right-angled triangle are from the perspective of a particular non-right angle.
In a right-angled triangle, two such angles are there which are not right angled(not of 90 degrees).
The slanted side is called the hypotenuse.
Let d the horizontal distance from the base of the skyscraper out to the ship. Since the angle of depression is 45°, hence:
\(\text{Angle} = 90 - 45 = 45^o\)
Using trigonometric ratio:
\(tan(45) = \dfrac{d}{1053}\)
\(d = 1053\ \text{feet}\)
The horizontal distance from the base of the skyscraper out to the ship would be 1053 feet.
Find out more on trigonometric ratio at:
https://brainly.com/question/24349828
In the right △ABC with m∠C=90°, m∠B=75°, and AB=12 cm. Find the area of △ABC.
Don't use trig to solve, don't know how to.
Answers
The area of the right triangle is 18.02 cm².
How to find area of a right triangle?A right angle triangle is a triangle that has one of its angles as 90 degrees.
The sum of angles in a triangle is 180 degrees.
Therefore, let's find the area of the right angle triangle as follows;
let's find the height and base of the triangle.
using trigonometric ratios,
cos 75 = adjacent / hypotenuse
cos 75 = base / 12
base = 3.10582854123
Therefore,
sin 75 = opposite / hypotenuse
sin 75 = h / 12
height = 11.5911099155
height = 11.59
Therefore,
area of the triangle = 1 / 2 × 3.11 × 11.59
area of the triangle = 36.0483518371 / 2
area of the triangle = 18.0241759186
area of the triangle = 18.02 cm²
learn more on area here: brainly.com/question/22965641
#SPJ1
Select the correct answer from the drop-down menu. The missing term in the denominator is
Answers
Answer: where is the answer choices
Step-by-step explanation:
Can someone help me with thisss plssss it’s due today

Answers
Part A: The equation of the circle in standard form is x² + (y - 7)² = 2².
Part B: Center: (h, k) = (0, 7), Radius: 2
Part C: Please check the attachment.
How to analyze and graph the equation of a circle
In this problem we find the definition of the equation of a circle in general form, whose standard form must be found:
(x - h)² + (y - k)² = r²
Where:
(h, k) - Coordinates of the center.r - RadiusThis can be done by completing the square. First, write the equation of the circle:
x² + y² = 14 · y - 45
Second, complete the square by algebra properties:
x² + y² - 14 · y + 45 = 0
x² + (y² - 14 · y + 49) = 4
x² + (y - 7)² = 2² (PART A)
Third, write the coordinates of the center and the radius of the circle:
Center: (h, k) = (0, 7), Radius: 2 (PART B)
Finally, we proceed to graph the resulting expression.
To learn more on equations of circles: https://brainly.com/question/29288238
#SPJ1

Can u pleaseee answer all parts pleaseeeee <3333
please help meee


Answers
a. In interval notation, Increasing intervals: (12pm, 1pm) U (1pm, 2pm) U (2pm, 3pm). Decreasing intervals: (8am, 9am) U (11am, 12pm). Constant intervals: (9am, 10am) U (10am, 11am)
b. The increase in cost between 12 noon and 3 pm is $2.
c. Yellow Cab has a lower price per 1km than Swift ride at (8am, 9am) (9am, 10am) (2pm 3pm)
How do you express a data set in interval notations?Interval notation is used to represent continuous intervals of numbers or values, like ranges on a number line.
The graph shows that from 8-9am, and 11-12pm, the cost from Swift Ride decreases.
We can represent it as (8am, 9am) U (11am, 12pm).
It increases at these times (12pm, 1pm) U (1pm, 2pm) U (2pm, 3pm).
And stays constant at : (9am, 10am) U (10am, 11am)
Cost increase from 12 to 3pm,We simply deduct the 12pm's cost from 3pm's cost.
So, we have
Cost increase = $3.5 - $1.5
Evaluate the difference
Cost increase = $2
Hence, the cost increase is $2
The time interval where the cost is lowerWhen you plot the points provided for Yellow cab, you'll notice that Yellow Cab has a lower price per 1km than Swift ride at (8am, 9am) (9am, 10am) (2pm 3pm)
Find more exercises on Interval notation;
https://brainly.com/question/17249352
#SPJ1
The sum of the reciprocals of two consecutive even integers is 9/40
This can be represented by the equation shown.
1/x +1/x+2 =9/40
Use the rational equation to determine the integers. Show all work.
Answers
Answer:
Only integer solution is x=8
Step-by-step explanation:
\(\displaystyle \frac{1}{x}+\frac{1}{x+2}=\frac{9}{40}\\\\\frac{x+2}{x^2+2x}+\frac{x}{x^2+2x}=\frac{9}{40}\\\\\frac{2x+2}{x^2+2x}=\frac{9}{40}\\\\40(2x+2)=9(x^2+2x)\\\\80x+80=9x^2+18x\\\\0=9x^2-62x-80\\\\0=x^2-62x-720\\\\0=(x-72)(x+10)\\\\0=(x-8)(9x+10)\\\\x=8,\,x=-\frac{10}{9}\)
Therefore, the only integer solution is x=8
4.2 The Court lines are 50 mm wide. Court paint covers 7 m² per litre of paint. 4.2.1 Calculate the total length of the centre circle and the two goal semi circles to be repainted. You may use the formula: Total length Circumference of a centre circle + 2 x Circumference of a semicircle =
Answers
The total length of the centre circle and the two goal semi circles to be repainted is 56.22 meters.
How to calculate the Calculate the total length of the centre circle and the two goal semi circles to be repaintedGiven:
Court lines are 50 mm wide.
Court paint covers 7 m² per litre of paint.
The centre circle is a complete circle, so the circumference is given by the formula: Circumference = 2πr
Radius of the entire circle = 9 m / 2 = 4.5 m
Radius of the centre circle = 4.5 m - 0.05 m (converted 50 mm to meters) = 4.45 m
Circumference of the centre circle = 2π(4.45 m) = 27.94 m
Next, let's calculate the circumference of the semicircles:
The semicircles are half circles, so the circumference is given by the formula: Circumference = πr
The radius (r) of the semicircles is the same as the radius of the entire circle, which is 4.5 m.
Circumference of a semicircle = π(4.5 m) = 14.14 m
Total length = Circumference of the centre circle + 2 x Circumference of a semicircle
Total length = 27.94 m + 2(14.14 m)
Total length = 56.22 m
Therefore, the total length of the centre circle and the two goal semi circles to be repainted is 56.22 meters.
Learn more about length at https://brainly.com/question/28322552
#SPJ1