Select and place the symbol that will make the statement true |-a| |a|
Answers
Answer:
|-a|=|a|
Step-by-step explanation:
The lines beside the a's mean that you are trying to find the absolute value of what's inside. The absolute value of something is the distance it is from 0. You can't have a negative distance so anything inside of absolute value line are positive.
Therefor this is how we can solve this.
|-a| __ |a|
a __ a
a=a
Related Questions
3. A bicycle has wheels with a diameter of 622 mm. The
bicycle rolls forward and the wheel turns 5 radians.
How many millimeters forward did the bicycle move?
Distance = ( ) (622) = (15.708) ()
= (2.618)
וחתן
Answers
Answer:
1553.6mm
Step-by-step explanation:
Given data
Diameter = 622mm
Radius= 622/2= 311mm
Circumference= 2πr
Circumference= 2*3.142*311
Circumference= 1954.32
Each revolution the wheels will turn 1954.32mm
Now let us convert radian to turns
1 radian= 0.159155 turns
5 radians= x turns
cross multiply
x= 5*0.159155
x=0.795 turns
If 1 turn will give 1954.32mm
0.795 turn will give x
cross multiply
x= 0.795*1954.32
x=1553.6mm
ASSESSMENT
Find the missing term:
1. 3:5= N: 15
2. N: 12-8: 24
3. 15: n= 60: 20
4. 9: 5= 27: n
5. 112: 24= N: 336
Answers
1. 9
2. 4
3. 5
4. 15
5. 1568
The graph of the function f(x) = –(x + 6)(x + 2) is shown below.
On a coordinate plane, a parabola opens down. It goes through (negative 6, 0), has a vertex at (negative 4, 4), and goes through (negative 2, 0).
Which statement about the function is true?
The function is increasing for all real values of x where
x < –4.
The function is increasing for all real values of x where
–6 < x < –2.
The function is decreasing for all real values of x where
x < –6 and where x > –2.
The function is decreasing for all real values of x where
x < –4.
Answers
The statement about the function is: "The function is decreasing for all real values of x where x < -4." D.
The given information tells us that the graph represents a downward-opening parabola.
The vertex of the parabola is located at (-4, 4) indicates that this point is the highest point on the graph.
As we move to the left of the vertex, the function values decrease, indicating a decreasing trend.
Moreover, the graph passes through the point (-6, 0), which lies to the left of the vertex.
This confirms that the function is decreasing for all real values of x less than -4, including x < -6.
On the other hand, the graph also passes through the point (-2, 0), which lies to the right of the vertex.
This does not impact the conclusion that the function is decreasing for x < -4, as the graph's behavior to the right of the vertex is not relevant to this particular statement.
Based on the given information and the properties of the downward-opening parabola, we can conclude that the function is decreasing for all real values of x where x < -4.
For similar questions on function
https://brainly.com/question/25638609
#SPJ11

Pleaseeee help I'll give Brainliest urgent!!!!!!!!!!!!!!!!!

Answers
Answer:
The answer is
'The range of the data for girls is less than the range of the data for boys'
I'm don't know dfhgh fhfghfg hgf hgfh
-77x - 78x = -155x
-66y - (-66y) = -66y + 66y = 0
264 - (-666) = 264 + 666 = 930
This leaves us with -155x = 930. Dividing by -155 on both sides, we find:
x = -6
Substitute x = -6 into one of the two original equations, solve for y, and then state the full solution to the system of equations.
Answers
Answer:
I don't understand
Step-by-step explanation:
You answer it.
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
Answers
Answer:
53\(x_{123}\) == 134 cf
Step-by-step explanation:
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
The height of the building is approximately 78.63 meters.
The following is a step-by-step explanation of how to solve the problem. We'll need to use some trigonometric concepts and formulas to find the solution.
Draw a diagram of the situation described in the problem to get a better understanding of the problem. The diagram would have a right-angled triangle with angle of elevation of 66° at the bottom left vertex and another angle of elevation of 53° at the bottom right vertex. The object on top of the building is at the vertex of the triangle. Point M and I on the diagram are points on the horizontal line of sight and on the ground respectively. We can label the diagram with the following values:Angle of elevation from point A = 66°Angle of elevation from point P = 53° Length of line segment AM = h Length of line segment MP = x Length of line segment IP = y Length of line segment MT = 50m. We'll use these values to calculate the length of h, which is the height of the building.Use the tangent ratio to find x:tan 66° = h / x => x = h / tan 66°. Use the tangent ratio to find y:tan 53° = h / y => y = h / tan 53°.We know that x + y = 50, so substituting the expressions for x and y from step 3 gives:h / tan 66° + h / tan 53° = 50h = 50 tan 66° tan 53° / (tan 53° + tan 66°) ≈ 78.63 m.Therefore, the height of the building is approximately 78.63 meters.
For more such questions on height, click on:
https://brainly.com/question/28122539
#SPJ8
6. What equation would you use to solve for x?*

Answers
Opposite over adjacent
How do you solve these? I guess I have to find how much they are in percents

Answers
Answer
1) 2500 %
2) 1800%
3) 3500%
Step-by-step explanation:Convert the decimal to a percentage by multiplying the decimal by 100 .
Round to the nearest angle. Plssss help:)

Answers
a^2 + 144 = 225
225 - 144 = 81
square root of 81 = 9
a = 9

Type the correct answer in each box.
Day Amount
1
$26
2
$23
3
$31
4
$26
5
534
The table shows the amount Bill spent on 5 days last week.
The mean of the amount he spent is $
The mean absolute deviation is $
Reset
Next
Answers
The mean absolute deviation is $106.6.
Given the table shows the amount Bill spent on 5 days last week.
DayAmount12622313126534To find the mean of the amount he spent: The formula for calculating the mean of a given set of values is mean=∑x/n where x represents the values, n represents the number of values, and ∑x represents the sum of the values.
Mean=total sum of values/total number of values Mean=(26+23+31+26+534)/5Mean=640/5Mean=128So,
the mean of the amount he spent is $128.To find the mean absolute deviation: The mean absolute deviation (MAD) is the average distance between each data value and the mean. MAD shows how much the data set deviates from the mean. The formula for calculating the MAD is MAD=∑|xi−m|/n where xi represents the values, m represents the mean, and n represents the number of values. So, the calculation for each day is:
Day Amount Absolute deviation from mean1 26 |128-26|=102 23 |128-23|=105 31 |128-31|=974 26 |128-26|=102 534 |128-534|=406
The sum of all absolute deviations is:
10+10+97+10+406=533The mean absolute deviation (MAD) is: MAD=533/5=106.6So.
For more question deviation
https://brainly.com/question/475676
#SPJ8
Find the unit price of 48 golf balls for $38.97. Round your answer to the nearest cent if necessary.
Answers
Answer:
.81
Step-by-step explanation:
38.97/48=.811875
Answer:
$0.81
Step-by-step explanation:
Hi there!
To find the unit price of the golf balls, divide the total cost by the total number of golf balls:
$38.97 ÷ 48
= $0.81 (approximately)
Therefore, the unit price is $0.81.
I hope this helps!
PLEASE HELP ME ASAP !!!!

Answers
Answer:
33.75
Step-by-step explanation:
.75×15=11.25
1.50×15=22.5
11.25+22.5=33.75
have a good day!
Answer = A)$33.75
Step-by-step explanation:
0.75+ 1.50 = 2.25
2.25 x 15 = 33.75
Please mark as brainliest if answer is right
Have a great day, be safe and healthy
Thank u
XD
18. If Allan swims at an average speed of 2
metres per second, how long will it take
him to complete a 200 metre race?
Answers
Answer:
100 seconds
Step-by-step explanation:
200/2 = 100s
A Triangle has a height that is half of 28 yards and an area of 56 yards^2. What is the length of the base of the trangle?
Answers
The length of the base of the triangle is 8 yards whose height is half of 28 yards.
What is triangle?A triangle is a two-dimensional geometric shape that is formed by three straight lines that connect three non-collinear points. These three lines are called the sides of the triangle, and the points where the sides meet are called the vertices of the triangle.
According to question:The following formula provides the area of a triangle:
Area = (1/2) x base x height
We are given that the height of the triangle is half of 28 yards, which is:
height = 1/2 x 28 = 14 yards
We are also given that the area of the triangle is 56 square yards. Substituting these values into the formula for the area, we get:
56 = (1/2) x base x 14
Simplifying this equation, we get:
56 = 7 x base
Dividing both sides by 7, we get:
base = 8
Therefore, the length of the base of the triangle is 8 yards.
The vertices are typically denoted by letters, such as A, B, and C. The three angles formed by the sides are also part of the triangle.
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
Calculate the side lengths a and b to two decimal places.

Answers
Answer:
D. a = 11.71 and b = 15.56
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASEquality PropertiesTrigonometry
All angles in a triangle add up to 180°Pre-Calculus
Law of Sines: \(\frac{sin(A)}{a} =\frac{sin(B)}{b} =\frac{sin(C)}{c}\)Step-by-step explanation:
Step 1: Define
AC = b
CB = a
AB = 7
m∠A = 45°
m∠B = 110°
m∠C = ?
Step 2: Find missing ∠
Set up equation: m∠C + 45° + 110° = 180°Combine like terms: m∠C + 115° = 180°Isolate unknown: m∠C = 25°Step 3: Find measure of b
Substitute: \(\frac{sin(25)}{7} =\frac{sin(110)}{b}\)Cross-multiply: \(bsin(25)=7sin(110)\)Isolate b: \(b=\frac{7sin(110)}{sin(25)}\)Evaluate: \(b=15.5645\)Round: \(b \approx 15.56\)Step 4: Find measure of a
Substitute: \(\frac{sin(25)}{7} =\frac{sin(45)}{a}\)Cross-multiply: \(asin(25)=7sin(45)\)Isolate a: \(a=\frac{7sin(45)}{sin(25)}\)Evaluate: \(a=11.7121\)Round: \(a \approx 11.71\)Answer:
Answer is D
Step-by-step explanation:
Please solve with elimination
5x + 9y =-5
3x -8y = -3
help I will give brainliest
please show work
Answers
Answer:
Step-by-step explanation:
5x+9y=-3 Multiply both sides by 8
40x+72y=-24
-53x-8y=-3 Multiply both sides by 9
-477x -72y= -27
sum the equations vertically to eliminate one variable
40x+72y= -24
-477x-72y= -27 (the y cancels out )
-477x =-51 (-24 + -27=-51)
-477x=-51 / -477 divide both sides by -477
x =51/437
5x 51/437=9y= -3 substitute the value of x
y= -174 /437
(x,y) = (51/437, -174/437)
simplify 1/x-10 / 9x/x2-9x-10
Answers
The simplified expression is \(\frac{-1}{9x} -9x - 10\).
What is algebraic expression?An algebraic expression in mathematics is an expression which is made up of variables and constants, along with algebraic operations (addition, subtraction, etc.).
Here, the given expression
\(\frac{1}{x}+\frac{-10x/9}{x^2}-9x-10\)
\(\frac{1}{x}+\frac{-10}{9x}-9x-10\)
\(\frac{9-10}{9x} -9x -10\)
\(\frac{-1}{9x} -9x - 10\)
Thus, the simplified expression is \(\frac{-1}{9x} -9x - 10\).
Learn more about Algebraic expression from:
https://brainly.com/question/19245500
#SPJ1
maths question, been stuck on for ages
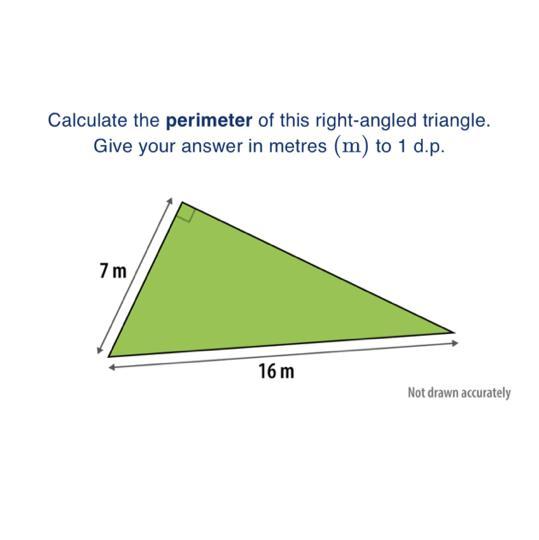
Answers
Answer:
14.4
Step-by-step explanation:
1) 16^2-7^2=207
2) square root of 207 is 14.4 (to 1 decimal place).
A shoe manufacturer claims that among the general adult population in the United States that the length of the left foot is longer than the length of the right foot. To compare the average length of the left foot with that of the right foot, we will take a random sample of adults and measure the length of the left foot and then the length of the right foot. Based on our sample, does the data indicate that the length of the left foot is greater than the length of the right foot? Is the hypothesis one-tailed or two-tailed?
Answers
We can reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis that the left foot is longer than the right foot.
How to test the data indicate that the length of the left foot is greater than the length of the right foot?A statistical test is required to determine whether the length of the left foot is greater than the length of the right foot. The null hypothesis states that there is no difference in average length between the left and right feet. The alternative hypothesis is that the left foot's average length is greater than the right foot's average length.
This hypothesis is one-tailed, as we are only interested in whether the left foot is longer than the right foot. We are not considering the possibility that the right foot could be longer than the left foot.
A t-test can be used to determine whether the difference in average length between the left and right feet is statistically significant. We can reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis that the left foot is longer than the right foot if the p-value of the t-test is less than the chosen significance level (e.g., 0.05).
Learn more about null hypothesis at https://brainly.com/question/25263462
#SPJ1
Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27). f(x) = -x3 - 4x2 + 3x. Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
Answers
The ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) do not correspond to the intervals where the graph of f(x) is decreasing. The pairs (1, -2) and (-3, -18) are the correct ones.
To determine where the graph of f(x) is decreasing, we need to examine the intervals where the function's derivative is negative. The derivative of f(x) is given by f'(x) = -3x^2 - 8x + 3.
Now, let's evaluate f'(x) for each of the given x-values:
f'(-1) = -3(-1)^2 - 8(-1) + 3 = -3 + 8 + 3 = 8
f'(2) = -3(2)^2 - 8(2) + 3 = -12 - 16 + 3 = -25
f'(0) = -3(0)^2 - 8(0) + 3 = 3
f'(1) = -3(1)^2 - 8(1) + 3 = -3 - 8 + 3 = -8
f'(-3) = -3(-3)^2 - 8(-3) + 3 = -27 + 24 + 3 = 0
f'(-4) = -3(-4)^2 - 8(-4) + 3 = -48 + 32 + 3 = -13
From the values above, we can determine the intervals where f(x) is decreasing:
f(x) is decreasing for x in the interval (-∞, -3).
f(x) is decreasing for x in the interval (1, 2).
Now let's check the ordered pairs in the table:
(-1, -6): Not in a decreasing interval.
(2, -18): Not in a decreasing interval.
(0, 0): Not in a decreasing interval.
(1, -2): In a decreasing interval.
(-3, -18): In a decreasing interval.
(-4, -12): Not in a decreasing interval.
Therefore, the ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) are not located in the intervals where the graph of f(x) is decreasing. The correct answer is: (1, -2), (-3, -18).
For more question on intervals visit:
https://brainly.com/question/30460486
#SPJ8
Note the complete and the correct question is
Q- Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27).
\(f(x) = -x^3 - 4x^2 + 3x\).
Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
The following are ages of 17 of the signers of the Declaration of Independence.
49, 34, 42, 43, 39, 36, 50, 44, 45, 33, 34, 27, 33, 69, 46, 50, 41
Send data to calculator
Find 25th and 80th percentiles for these ages.
(If necessary, consult a list of formulas.)
(a) The 25th percentile:
The 80th
percentile:
Answers
Answer:
Step-by-step explanation:
The problem specifies that you may use a calculator. The formula, as reference, is:
You can use a regular calculator or an online spreadsheet to solve. In sheets, arrange your data and use the =PERCENTILE( ) function. In the parentheses, write the range of your data and the requested percentile as a decimal. So if I type the data (the ages of the signers for this example) in cells A:4 through A:23, I'd write =percentile(A7:A23,0.25).
So the answers:
25th percentile is 34.
80th percentile is 48.4.
what is the value of x in the figure Pls help

Answers
Answer: x=18
im assuming that this is a right angle
so if it is then that means the total of the angle should be 90 degrees. so 2x+3x should be equal to 90. Just combine like terms to get that 5x=90 and then isolate the variable (divide by 5 on both sides) so x ends up equaling 18.
so x=18
I need help with math asap
Answers
um where’s the question?
Calc II Question
The base of s is an elliptical region with boundary curve 9x^2 + 4y^2 = 36
Cross sections perpendicular to the x axis are isoscelees right triangle with hypotension in the base.
Correct answer is 24 but I don't know how they go that
Answers
Answer:
See below for explanation
Step-by-step explanation:
The area of an isosceles triangle is \(A=\frac{1}{2}bh\), so let's write the base as an equation of y:
\(\displaystyle 9x^2+4y^2=36\\\\4y^2=36-9x^2\\\\y^2=9-\frac{9}{4}x^2\\\\y=\pm\sqrt{9-\frac{9}{4}x^2\)
As you can see, our ellipse consists of two parts, so the hypotenuse of each cross-section will be \(\displaystyle 2\sqrt{9-\frac{9}{4}x^2\), and each height will be \(\displaystyle \sqrt{9-\frac{9}{4}x^2}\).
Hence, the area function for our cross-sections are:
\(\displaystyle A(x)=\frac{1}{2}bh=\frac{1}{2}\cdot2\sqrt{9-\frac{9}{4}x^2}\cdot\sqrt{9-\frac{9}{4}x^2}=9-\frac{9}{4}x^2\)
Since we'll be integrating with respect to x because the cross-sections are perpendicular to the x-axis, then our bounds will be from -2 to 2 to find the volume:
\(\displaystyle V=\int^2_{-2}\biggr(9-\frac{9}{4}x^2\biggr)\,dx\\\\V=9x-\frac{3}{4}x^3\biggr|^2_{-2}\\\\V=\biggr(9(2)-\frac{3}{4}(2)^3\biggr)-\biggr(9(-2)-\frac{3}{4}(-2)^3\biggr)\\\\V=\biggr(18-\frac{3}{4}(8)\biggr)-\biggr(-18-\frac{3}{4}(-8)\biggr)\\\\V=(18-6)-(-18+6)\\\\V=12-(-12)\\\\V=12+12\\\\V=24\)
Therefore, this explanation confirms that the correct volume is 24!
Describe a series of transformations that moves the blue figure to the red figure Be specific! If there is a : Translation - show number and direction Reflection - give axis of reflection Rotation - give direction (clockwise or counterclockwise) and degree amount

Answers
The blue figure is moved 5 units to the right (T(5, 0)), reflected in the y-axis (r(y-axis)), and then rotated 90 degrees counterclockwise (R(-90)).
Translation: Move the blue figure 5 units to the right (translation of 5 units to the right, denoted as T(5, 0))
Reflection: Reflect the figure in the y-axis (denoted as r(y-axis))
Rotation: Rotate the figure 90 degrees counterclockwise (denoted as R(-90))
The series of transformations that moves the blue figure to the red figure is T(5, 0) followed by r(y-axis) followed by R(-90).To better understand this, let's break down the transformations. The first transformation is a translation, which is a movement of a figure from one location to another. In this case, the figure is being moved 5 units to the right. This is denoted as T(5, 0).The second transformation is a reflection, which is a flip of a figure over a line or axis. In this case, the figure is being reflected in the y-axis. This is denoted as r(y-axis).The third transformation is a rotation, which is a turn of a figure around a point. In this case, the figure is being rotated 90 degrees counterclockwise. This is denoted as R(-90).Therefore, the series of transformations that moves the blue figure to the red figure is T(5, 0) followed by r(y-axis) followed by R(-90).
Learn more about unit here
https://brainly.com/question/19866321
#SPJ1
PLEASE HELP FAST !!!!!
The distribution of pitches thrown in the
80 at-bats in a baseball game is as follows.
Pitches 1 2 3 4 5
Frequency 12 16 32 12 8
Find the relative frequency that the pitcher
will throw exactly 4 pitches in an at-bat.
?
Relative Frequency =
Do NOT simplify your answer.

Answers
The relative frequency of the pitcher throwing exactly 4 pitches in an at-bat is given as follows:
3/20.
How to calculate a relative frequency?A relative frequency is calculated as the division of the number of desired outcomes by the number of total outcomes.
The total number of at bats in this problem is given as follows:
80.
In 12 of them, the pitcher threw exactly four pitches, hence the relative frequency of the pitcher throwing exactly 4 pitches in an at-bat is given as follows:
12/80 = 3/20.
More can be learned about relative frequencies at brainly.com/question/1809498
#SPJ1
will give brainliest

Answers
Answer:
About 8.2 cm
Step-by-step explanation:
Assuming that a is one of the legs of this right triangle, then using the Pythagorean Theorem:
\(a=\sqrt{15.3^2-12.9^2}\approx 8.2\)
Hope this helps!
Solve for mZIJL.
K
\100°
52°
o
Answer: mZIJL
Submit Answer

Answers
Answer:
m<IJL = 48
Step-by-step explanation:
<IJL = x
100 - 52 = x
x = 48
5. Round 16.975 to the nearest hundredths
A 16.10
B. 16.98 C. 16.20 D. 16.97
6. Encircle the letter of the number that rounds off to 10.85
A 10.859
B. 10.857 C. 10.851 D. 10.856
7. Which of the following order numbers from greatest to least?
a 3.756
37.56
375.6 0.3756
b. 0.2468
0.2486 0.2648 0.2846
C. 11.010
11.011 11.0110 1.1101
d. 2.86
2.75
2.68
2.56
Answers
Answer:
5. B
6. C
7. D
Step-by-step explanation:
hope this is correct and helps hehe
Help me asap and need the answer quick

Answers
Answer:20 m/s
Step-by-step explanation:
Answer:
20 m/s
Step-by-step explanation:
700 ÷ 35 = 20 m/s