Answers
Answer:
5 +4(n -1)
Step-by-step explanation:
The wording "the same number of sticks is added each time" tells you this is an arithmetic sequence. To find the rule, you need to know ...
the number of sticks in the first pattern: 5the number of sticks added each time: 4The form of the rule for the n-th term of an arithmetic sequence is ...
an = a1 +d(n -1) . . . . . . a1 = first term; d = common difference
For a1 = 5 and d = 4, your rule for the n-th pattern is ...
sticks in n-th pattern = 5 +4(n -1)
_____
This can be simplified to 1 +4n.
Related Questions
How do I get the exact value of sin 480?
Answers
Step 1
Remove full rotations of 360 degrees until the angle is between 0 and 360 degrees
\(480-360=120^o\)Step 2
Hence, we find sin 120 using reference angles in the first quadrant
\(\begin{gathered} \sin \text{ 60=}\frac{\sqrt[]{3}}{2} \\ \text{Hence} \\ \sin 120=\frac{\sqrt[]{3}}{2} \end{gathered}\)Therefore,
\(\begin{gathered} \sin 480=\sin 120=\sin 60=\frac{\sqrt[]{3}}{2} \\ \sin \text{ 480=}\frac{\sqrt[]{3}}{2} \end{gathered}\)Answer sin 480 =(√3)/2
In developing patient appointment schedules , a medical centre wants to estimate the mean time that a staff member spends with each patient. How large a sample should be taken if the desired margin of error is 2 minutes at a 95 per cent level of confidence? How large a sample should be taken for a 99 per cent level of confidence ? Use a planning value for the population standard deviation of 8 minutes.
Answers
A. A sample size of 62 should be taken for a 95% level of confidence.
B. The sample size of 107 should be taken for a 99% level of confidence.
a. To estimate the sample size needed to estimate the mean time a staff member spends with each patient, we can use the formula for sample size calculation:
n = (Z^2 * σ^2) / E^2
Where:
n = required sample size
Z = Z-score corresponding to the desired level of confidence
σ = population standard deviation
E = desired margin of error
For a 95% level of confidence:
Z = 1.96 (corresponding to a 95% confidence level)
E = 2 minutes
σ = 8 minutes (population standard deviation)
Substituting these values into the formula:
n = (1.96^2 * 8^2) / 2^2
n = (3.8416 * 64) / 4
n = 245.9904 / 4
n ≈ 61.4976
Since we can't have a fraction of a sample, we round up the sample size to the nearest whole number. Therefore, a sample size of 62 should be taken for a 95% level of confidence.
b. For a 99% level of confidence:
Z = 2.58 (corresponding to a 99% confidence level)
E = 2 minutes
σ = 8 minutes (population standard deviation)
Substituting these values into the formula:
n = (2.58^2 * 8^2) / 2^2
n = (6.6564 * 64) / 4
n = 426.0096 / 4
n ≈ 106.5024
Rounding up the sample size to the nearest whole number, a sample size of 107 should be taken for a 99% level of confidence.
Learn more about sample size :
brainly.com/question/25894237
#SPJ11
are births of newborn babies uniformly distributed across the days of the week? a random sample of 700 births from local records shows this distribution
Answers
Based on the information provided, we can assume that the sample of 700 births is representative of the population of births in the local area. The distribution of these 700 births across the days of the week can be analyzed to determine whether or not newborn babies are uniformly distributed across the days of the week.If the distribution of the 700 births is approximately equal across all seven days of the week, then we can conclude that newborn babies are uniformly distributed. However, if the distribution is significantly different from what would be expected if births were uniformly distributed, then we can conclude that there may be a non-uniform pattern of births.
Without knowing the actual distribution of the 700 births, we cannot definitively answer this question. However, if the distribution is close to equal, then we can tentatively say that newborn babies are uniformly distributed across the days of the week.
Learn more about uniformly distributed here :brainly.com/question/30657467
#SPJ11
What is the equation of the line that is the parallel to x - 8y = 16 and passes throguh the point (-8, 2)
Answers
Answer:
Step-by-step explanation:
x - 8y = 16
Write in slope-intercept form: y = mx + b
-8y = -x + 16
Divide the entire equation by (-8)
\(y =\dfrac{-1}{-8}x+\dfrac{16}{-8}\\\\\\y=\dfrac{1}{8}x-2\)
Parallel lines have slope. So, the slope of the required line = 1/8
\(y =\dfrac{1}{8}x+b\\\\\\\)
(-8,2) is on the line. so, plugin the values in the above equation and find the y-intercept b
\(2=\dfrac{1}{8}*(-8)+b\\\\\\2=-1+b\\\\b = 2+1\\\\b = 3\\\\Equation \ of \ the \ required \ line:\\\\y=\dfrac{1}{8}x+3\)
Answer:
\(\displaystyle x - 8y = -24\:or\:y = \frac{1}{8}x + 3\)
Step-by-step explanation:
First off, convert this standard equation to a Slope-Intercept equation:
\(\displaystyle x - 8y = 16 \hookrightarrow \frac{-8y}{-8} = \frac{-x + 16}{-8} \\ \\ \boxed{y = \frac{1}{8}x - 2}\)
Remember, parallel equations have SIMILAR RATE OF CHANGES, so ⅛ remains as is as you move forward with plugging the information into the Slope-Intercept Formula:
\(\displaystyle 2 = \frac{1}{8}[-8] + b \hookrightarrow 2 = -1 + b; 3 = b \\ \\ \boxed{\boxed{y = \frac{1}{8}x + 3}}\)
Now, suppose you need to write this parallel equation in Standard Form. You would follow the procedures below:
y = ⅛x + 3
- ⅛x - ⅛x
__________
−⅛x + y = 3 [We CANNOT leave the equation this way, so multiply by –8 to eradicate the fraction.]
−8[−⅛x + y = 3]
\(\displaystyle x - 8y = -24\)
With that, you have your equation(s).
\(\displaystyle -x + 8y = 24\)
*About this equation, INSTEAD of multiplying by –8, you multiply by its oppocite, 8. Now, you can leave it like this, but UNIVERSALLY, the A-term is positive, so you must multiply the negative out as well.
I am joyous to assist you at any time.
a bag has 60 cubes a random sample of 15 cubes is collected from the bag the results from the random sample are shown below. 5 red cubes 5 blue cubes 3 green cubes 2 white cubes
Answers
The expected amount of each cube in the complete bag is given as follows:
20 blue cubes.20 red cubes.12 green cubes.8 white cubes.How to obtain the expected amounts?The expected amounts are obtained applying the proportions in the context of the problem.
15 cubes were selected from a bag of 60, hence the fraction collected is given as follows:
15/60 = 1/4.
Meaning that the expected amounts on the bag are given by the amounts on the sample multiplied by 4.
Missing InformationThe problem asks for the expected amount of each cube in the complete bag.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
what is the probability of drawing (without replacement) an ace, then a king, and then a queen, from a regular deck of 52 cards?
Answers
Three cards are drawn from a standard deck. Thus, the probability to get an ace, followed by a king, and then a queen, is 16/34,425
The formula for conditional probability is:
P(A∩B) = P(B|A) . P(A)
In the given problem:
P(ace) = 4 / 54
After an ace was drawn, the number of cards now is 51.
Hence,
P(king | ace) = 4/51
After the second drawn, the remaining cards is 50. Hence,
P(queen | (king | ace)) = 4/50
Therefore,
P(ace,king,queen) = 4/54 x 4/51 x 4/50 = 64 / 137,700 = 16/34,425
Thus, the probability to get an ace, followed by a king, and then a queen, is 16/34,425
Learn more about conditional probability here:
https://brainly.com/question/28167698
#SPJ4
i literally have no clue what this unit is about so help

Answers
Answer:
4) √41 cm5) 8 cm or √514 cmStep-by-step explanation:
#4According to Pythagorean:
c² = a² + b²c² = 4² + 5² = 16 + 25 = 41c = √41#5Two sides are 15 cm and 17 cm
If the third side is hypotenuse, its length is:
c = √(15² + 17²) = √514 cmIf the third side is leg, its length is:
a = √(17² - 15²) = √64 = 8 cm
#4
Apply Pythagorean theorem
H²=P²+B²H²=4²+5²H²=16+25H²=41H=√41cm#5
If base
√17²-15²√8²8If Hypotenuse
√17²+15²=√514PLEASE HELP THIS IS MY LAST QUESTION:
Figure ABCD is a rhombus. If angle AEB = 5x-20, Find the value of x.
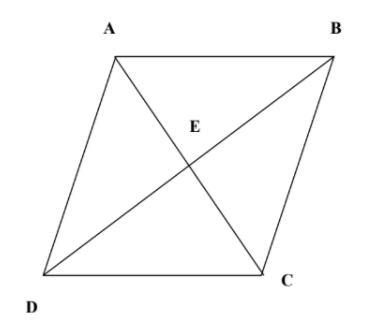
Answers
Answer:
22 is x
Step-by-step explanation:
diagonal of rhombus make 90° on intersection
5x-20 = 90
5x = 110
x = 22
Which is the graph of y=3/4x-3?
Graph B
Graph C
Graph A

Answers
Answer:
Graph A
Step-by-step explanation:
What does the x equal

Answers
Ron packed 37 oranges. He wants to put them in crates. Each crate holds four equal rows of three oranges. How many crates can he fill with oranges? Will there be any left over?
Pls put ur answer in words
Answers
Answer:
He can fill 3 crates, there would be 1 orange left over
Step-by-step explanation:
four equal rows of three oranges = 12 total. 12x3= 36, so 1 left over
assume that a normal distribution of data has a mean of and a standard deviation of use the empirical rule to find the percentage of values that lie .
Answers
Answer:
Assuming a normal distribution of data with a mean μ and a standard deviation σ, we can use the empirical rule to find the percentage of values that lie within a certain range.
The empirical rule states that for a normal distribution:
- Approximately 68% of the values lie within one standard deviation of the mean.
- Approximately 95% of the values lie within two standard deviations of the mean.
- Approximately 99.7% of the values lie within three standard deviations of the mean.
Based on this rule, we can determine the percentage of values that lie within different ranges. For example:
- Within one standard deviation: Approximately 68% of the values.
- Within two standard deviations: Approximately 95% of the values.
- Within three standard deviations: Approximately 99.7% of the values.
Please note that the exact percentage may vary depending on the specific values of the mean and standard deviation. It is important to calculate the values based on the actual mean and standard deviation provided.
Learn more about the empirical rule and normal distributions here:
https://brainly.com/question/31360738
#SPJ11
Which term describes the point where the three angle bisectors of a triangle
intersect?
A. Centroid-
B. Incenter
C. Circumcenter
D. Orthocenter
Answers
Answer:
Below.
Step-by-step explanation:
That is the incenter.
The point where the three angle bisectors of a triangle intersect is called as the incenter of the triangle
What is a Triangle?A triangle is a plane figure or polygon with three sides and three angles.
A Triangle has three vertices and the sum of the interior angles add up to 180°
Let the Triangle be ΔABC , such that
∠A + ∠B + ∠C = 180°
The area of the triangle = ( 1/2 ) x Length x Base
For a right angle triangle
From the Pythagoras Theorem , The hypotenuse² = base² + height²
if a² + b² = c² , it is a right triangle
if a² + b² < c² , it is an obtuse triangle
if a² + b² > c² , it is an acute triangle
Given data ,
Let the triangle be represented as ΔABC
Now , the measure of angles are ∠A , ∠B , ∠C
where the three angle bisectors are drawn
Now , point where the three angle bisectors of a triangle intersect is the incenter of the triangle
And , when all three angles of a triangle's bisectors come together at a location inside a circle, all three triangle vertices are equally far from that point.
Hence , triangle's incenter is also the center of the biggest circle that can be encircled by the triangle.
To learn more about triangles click :
https://brainly.com/question/16739377
#SPJ5
a measurable part of a line that consists of two points, called endpoints, and all of the points between them are
Answers
A measurable part of a line that consists of two points, called endpoints, and all of the points between them are called Line sigments.
Geometry is a branch of mathematics that deals with how objects can be expressed as relationships of points, lines, planes, surfaces, and dimensions. When we draw lines in geometry, we use an arrow at each end to show that it expands infinitely. A line is a path between two points that can be measured. Since line segments have a defined length, they can form the sides of any polygon. The figure below shows the line AB, where the length of the line AB is related to the distance between its endpoints, A and B. The symbol for the line is named after its two endpoints, e.g.
\( \bar{AB}\)
To learn more about line segment, refer:
https://brainly.com/question/28962970
#SPJ4

the sum of four consecutive odd numbers is 368 find the numbers
Answers
Answer:
the four consecutive numbers are 89, 90, 91, 93.
Step-by-step explanation:
let the four consecutive numbers be x, x+2, x+4, x+6
according to the condition in the question
x+x+2+x+4+x+6=368
4x+12=368
4x=356
x= 89
So, the numbers are 89, 90, 91, 93.
hope this will help :)
13 = -9.2x
Plz help I will give brainliest
Answers
Answer:
The equation rewritten in standard from --->
46x = 65.
solution --> x = 65/46
Alternate form --> x = 1 19/46, x = 1.41
answer to –1.7+5.2(5.5+–10.8a)
Answers
Answer:
26.9 - 56.16a
Step-by-step explanation:
-1.7 + 5.2(5.5 - 10.8a)
use the distributive property
-1.7 + 28.6 - 56.16a
combine like terms
-1.7 + 28.6 = 26.9
26.9 - 56.16a
plz mark as brianliest if correct!!!
after 4,000 gallons of water were added to a large water tank that was already filled to 3 4 of its capacity, the tank was then at 4 5 of its capacity. how many gallons of water does the tank hold when filled to capacity
Answers
Answer: #The tank holds 80,000 gallons of water when filled to capacity.
Step-by-step explanation:
I believe you meant 3/4 and 4/5 capacity...kindly check to confirm the error. The way to got about it is:Take the capacity of the tank after being filled with 4000 gallons of water (4/5) and subtract the value given of the capacity of the tank before being filled with water (3/4)4/5 - 3/4 = 1/20
The fraction (1/20) represents the 4000 gallons of water.
When filled to capacity the fraction of the tank will be whole (1) thus,1/20 = 4,000
1 =?
then u cross multiply
1*4,000*20/1
= 80,000 gallons of water
Know more about this here:
https://brainly.com/question/14103405
You are a local farmer and you participate in the local farmer's market, which is open 8am-6pm on Fri, Sat, and Sun. The organization charges a $50 flat fee for registering and $10/hr for a stand. If you plan to be there for the entirety, what will it cost?
Answers
Answer:
$350
Step-by-step explanation:
8-6 is 10 hours per day
3 days x 10 hours per day gives you 30 hours
30 hours x $10 per hour gives you $300
$300 plus the $50 flat fe gives you $350 in total
An object was launched off the top of a building. The function f(x)=-16x^2+16x+672 represents the height of the object above the ground, in feet, x seconds after being launched. Find and interpret the given function values and determine an appropriate domain for the function.
Answers
Answer:
6x2 + 16x = 672
Reorder the terms:
16x + 16x2 = 672
Solving
16x + 16x2 = 672
Solving for variable 'x'.
Reorder the terms:
-672 + 16x + 16x2 = 672 + -672
Combine like terms: 672 + -672 = 0
-672 + 16x + 16x2 = 0
Factor out the Greatest Common Factor (GCF), '16'.
16(-42 + x + x2) = 0
Factor a trinomial.
16((-7 + -1x)(6 + -1x)) = 0
Ignore the factor 16.
Subproblem 1
Set the factor '(-7 + -1x)' equal to zero and attempt to solve:
Simplifying
-7 + -1x = 0
Solving
-7 + -1x = 0
Move all terms containing x to the left, all other terms to the right.
Add '7' to each side of the equation.
-7 + 7 + -1x = 0 + 7
Combine like terms: -7 + 7 = 0
0 + -1x = 0 + 7
-1x = 0 + 7
Combine like terms: 0 + 7 = 7
-1x = 7
Divide each side by '-1'.
x = -7
Simplifying
x = -7
Subproblem 2
Set the factor '(6 + -1x)' equal to zero and attempt to solve:
Simplifying
6 + -1x = 0
Solving
6 + -1x = 0
Move all terms containing x to the left, all other terms to the right.
Add '-6' to each side of the equation.
6 + -6 + -1x = 0 + -6
Combine like terms: 6 + -6 = 0
0 + -1x = 0 + -6
-1x = 0 + -6
Combine like terms: 0 + -6 = -6
-1x = -6
Divide each side by '-1'.
x = 6
Simplifying
x = 6
Solution
x = {-7, 6}
Step-by-step explanation:
The given quadratic function models the projectile of the object as it is
launched off the top of the building.
The interpretation of the function values are;
The maximum height reached by the object is 676 feetThe height of the building is 672 feetTime of flight of the object is 7 secondsThe appropriate domain is 0 ≤ x ≤ 7
Reasons:
The given function for the height of the object is f(x) = -16·x² + 16·x + 672
The domain is given by the values of x for which the value of y ≥ 0
Therefore, when -16·x² + 16·x + 672 = 0, we get;
-16·x² + 16·x + 672 = 0
16·(-x² + x + 42) = 0
-x² + x + 42 = 0
x² - x - 42 = 0
(x - 7)·(x + 6) = 0
x = 7, or x = -6
The minimum value of time, x is 0, which is the x-value at the top of the
building, and when x = 7, the object is on the ground.
Therefore;
The appropriate domain is 0 ≤ x ≤ 7The maximum value of f(x) = a·x² + b·x + c, is given at \(x = -\dfrac{b}{2 \cdot a}\)
Therefore;
We have;
\(x = -\dfrac{16}{2 \times (-16)} = \dfrac{1}{2}\)
Which gives;
\(f \left(\frac{1}{2} \right) = -16 \times \left(\dfrac{1}{2} \right)^2 + 16 \times \left(\dfrac{1}{2} \right)+ 672 = 676\)
The maximum height reached by the object, \(f\left(\frac{1}{2} \right)\) = 676 feetThe height of the building is given when the time, x = 0, as follows;
Height of building, f(0) = -16 × 0² + 16 × 0 + 672 = 672
The height of the building, f(0) = 672 feetLearn more here;
https://brainly.com/question/10837575
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected from a sample of 64 business students over a one-week period. Assume the population standard deviation is 3.8 hours. The standard error of the mean is _____. a. 0.475 b. 1.805 x. 2.1 x. 0.059
Answers
The standard error of mean is option a) 0.475.
To estimate the standard error of the mean, we can use the formula:
Standard Error of the Mean = Population Standard Deviation / Square Root of Sample Size
In this case, the population standard deviation is given as 3.8 hours, and the sample size is 64. Plugging these values into the formula, we get:
Standard Error of the Mean = 3.8 / sqrt(64)
Simplifying this equation, we have:
Standard Error of the Mean = 3.8 / 8
Standard Error of the Mean = 0.475
So the correct answer is a. 0.475.
Learn more about standard error visit:
brainly.com/question/32854773
#SPJ11
On a coordinate plane, a curved line crosses the x-axis at (negative 1, 0) and crosses the y-axis at (0, 0.25). The line exits the plane at (negative 2, negative 6) and (2, 6).
Which statement is true about the end behavior of the graphed function?
As the x-values go to positive infinity, the function's values go to negative infinity.
As the x-values go to zero, the function's values go to positive infinity.
As the x-values go to negative infinity, the function's values are equal to zero
As the x-values go to positive infinity, the function's values go to positive infinity.
Answers
Answer: D) as x → ∞, y → ∞
Step-by-step explanation:
see graph
Notice that as x approaches negative infinity (goes to the left), the y-value decreases (goes toward negative infinity).
And as x approaches positive infinity (goes to the right), the y-value increases (goes toward positive infinity).

Answer:
D
Step-by-step explanation:
on the edge D
Add. Write your answer in simplest form.
G
1
3
x + 3 +
9) =
-x-9
Need help with this question?
Answers
The answer in simplest form is x = -3/4
What is an equation?
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =
The given equation is
3x + 3 +9 =-x-9
Collecting like terms to have
3x + x = -9+9-3
4x = -3
Making x the subject of the relation
Therefore, the value of x is x = -3/4
Learn more about equations on https://brainly.com/question/29657992
#SPJ1
What is the answer to the following?
(I need an answer today!!!

Answers
A plan is drawn using a scale of 1:500, if length of wall on palm is 6cm , how long is the wall in reality ?
Answers
Answer:
30 m
Step-by-step explanation:
500 x 6cm = 3000 cm = 30 m
Since the scale is 1:500, you can simply multiply the length you were given by 500.
500 * 6 = 3000
So the wall in reality will be 3000cm or 30m.
Consider the wave packet: ψ(x)=[ 2πa 2
1
] 1/2
exp[− 4a 2
(x−⟨x⟩) 2
+i ℏ
px
]. Calculate the uncertainties ⟨Δx 2
⟩=⟨( x
^
−⟨x⟩) 2
⟩ and ⟨Δp 2
⟩=⟨( p
^
−⟨p⟩) 2
⟩, where ⟨ A
^
⟩ denotes the expectation value ⟨ψ∣ A
^
∣ψ⟩ of the observable A
^
on the state ∣ψ>.
Answers
The uncertainties ⟨Δx^2⟩ and ⟨Δp^2⟩ are given by the expressions ⟨Δx^2⟩ = a^2/2 and ⟨Δp^2⟩ = (ℏ^2)/(8a^2).
To calculate the uncertainties ⟨Δx^2⟩ and ⟨Δp^2⟩ for the given wave packet, we need to find the expectation values of the observables (x^ - ⟨x⟩)^2 and (p^ - ⟨p⟩)^2, respectively.
The wave packet is represented by the function ψ(x) = [2πa^2]^(1/2) exp[-4a^2(x - ⟨x⟩)^2 + iℏpx]. Here, a is a constant, ⟨x⟩ represents the expectation value of x, and p is the momentum operator.
To find ⟨Δx^2⟩, we calculate the expectation value of (x^ - ⟨x⟩)^2 with respect to ψ(x). By integrating (x - ⟨x⟩)^2 multiplied by the squared magnitude of the wave packet over all x values, we obtain the result ⟨Δx^2⟩ = a^2/2.
Similarly, to find ⟨Δp^2⟩, we calculate the expectation value of (p^ - ⟨p⟩)^2 with respect to ψ(x). Since p is the momentum operator, its expectation value is ⟨p⟩ = 0 for the given wave packet. By integrating (p^ - 0)^2 multiplied by the squared magnitude of the wave packet over all x values, we obtain the result ⟨Δp^2⟩ = (ℏ^2)/(8a^2).
Therefore, the uncertainties ⟨Δx^2⟩ and ⟨Δp^2⟩ are given by the expressions ⟨Δx^2⟩ = a^2/2 and ⟨Δp^2⟩ = (ℏ^2)/(8a^2).
Learn more about Expressions
brainly.com/question/28170201
#SPJ11
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP

Answers
Answer:
i think that the answer is D. I did it wrong
Answer:
i think its D
Step-by-step explanation:
bc the 500 has to stay constant (so 500 cannot change to 501,502 etc)
gl for the rest of the questions
What is the area of the following circle?
Either enter an exact answer in terms of \piπpi or use 3. 143. 143, point, 14 for \piπpi and enter your answer as a decimal.
Answers
As a result, when the circle's radius is specified as 7 units, its area is 49 units, or 153.86 units2.
what is circle ?A circle is formed when every point in the plane that is a specific distance apart from another point does so (center). Thus, it is a curve made up of points that are separated from one another by a set distance while moving in the plane. It is also rotationally symmetric about the center at all angles. A circle is a closed, two-dimensional object where each pair of points in the plane is equally separated from the "center." A specular symmetry line is made by drawing a line through the circle. It is also rotationally symmetric about the center at all angles.
given
Radius of the circle
Radius, = d / 2 = 7
Area of the circle = pi * r * r = pi *49 = 49pi
Substituting the value of π = 3.14,
Area of the circle = 49 * 3.14 = 153.86 unit²
As a result, when the circle's radius is specified as 7 units, its area is 49 units, or 153.86 units2.
To know more about circle visit:
https://brainly.com/question/29142813
#SPJ4
all you need is in the photo

Answers
Answer:
Many solutions
Step-by-step explanation:
Name the relationship between x and y:

Answers
Answer:
They are the same angle.
Step-by-step explanation:
We have a diagonal line and two 180° parallel lines running through it. The x and y values should be identical because of the placement. The diagonal on the right and right above the 180° angle.
Option 2: Corresponding angles.
Hope this helps!
If not, I am sorry.
