Seventeen out of 20 teens said they eat breakfast every morning. What is the reasonable prediction for the number of teens out of 1,280 who eat breakfast every morning?
A.
340
B.
940
C.
1088
D.
1260
Answers
Answer:
The correct answer is C. 1088
Related Questions
how many feet of granite was tunneled through to make tunnel no. 6 through the sierra nevada mountains?
Answers
Nearly 1,659 feet of granite was tunnelled through to make tunnel no. 6 through the sierra Nevada mountains.
Early snowfall prevented the Central Pacific from starting construction on Tunnel No. 6, or the Summit Tunnel, in August 1865. It was built using a variety of engineering and construction methods and was located more than seven thousand feet above sea level.
When the workmen finally broke through, they discovered that they were only two inches off from the calculations that were used to locate its end points and central shaft. The length of the tunnel that was built through the Sierra Nevada mountains is therefore given as nearly 1,659 feet of granite was tunnelled through to make tunnel no. 6 through the Sierra Nevada mountains.
Read more about granite on:
https://brainly.com/question/880155
#SPJ4
7-5(x+6)= -7x-17 what value of x makes the equation true?
Answers
Answer:
x=3
Step-by-step explanation:
7-5(x+6)= -7x-17
Distribute
7 - 5x-30 = -7x-17
Combine like terms
-5x-23= -7x-17
Add 7x to each side
-5x-23+7x= -7x-17+7x
2x -23 = -17
Add 23 to each side
2x-23+23 = -17+23
2x= 6
Divide by 2
2x/2 = 6/2
x =3
Answer:
x = 3
Step-by-step explanation:
7 - 5(x + 6) = -7x - 17
~Simplify left side
7 - 5x - 30 = -7x - 17
~Combine like terms
-5x - 23 = -7x - 17
~Add 23 to both sides
-5x = -7x + 6
~Add 7x to both sides
2x = 6
~Divide 2 to both sides
x = 3
Best of Luck!
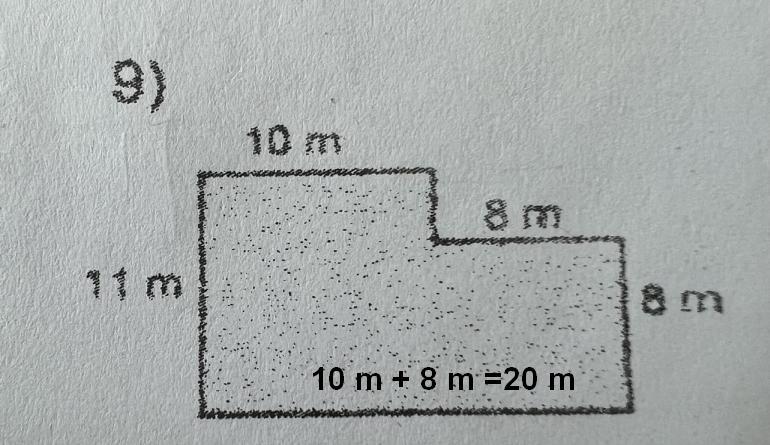
Find the perimeter of the figure below.
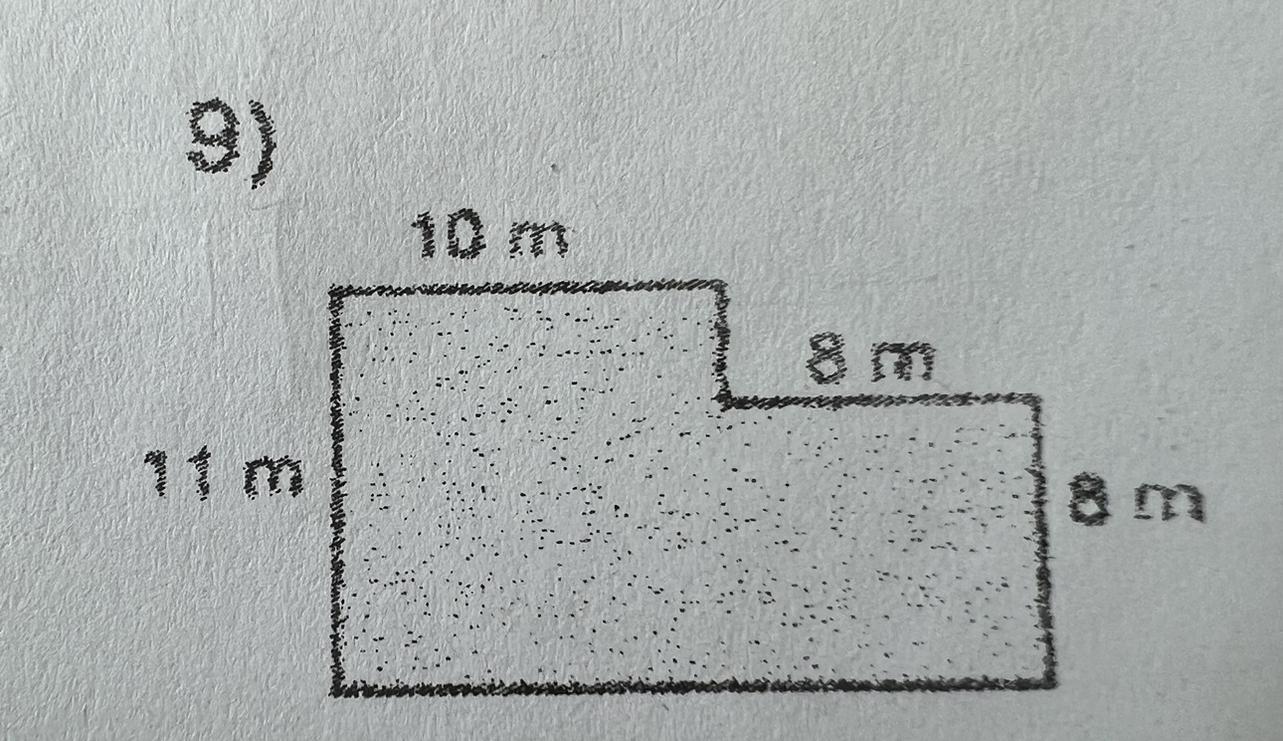
Answers
\(P=10\text{ m}+3\text{ m}+8\text{ m}+8\text{ m}+20\text{ m}+11\text{ m}=60\text{ m}\)
A circle above has a radius of 6 cm. What is the area of the circle?
Use = 3.14.
Answers
Answer:
113.04
Step-by-step explanation:
formula for area is
pi times radius times radius
if the radius is 6,
do 6 times 6=36
36 times 3.14=113.04
Arrange the equations in the correct sequence to find the inverse of f(2)=y==
33z-zy=y-4
33z +4=y(1+z)
33z-zy=y+4
33x+4=y+zy
1+z
y=f¹ (2) = 33274
+4
33z-zy = y +4
A =
33-
y=f-¹ (z) = 332+4
z (33-y)=y-4
↓
↓
↓
↓
Į
Answers
c ccccccccccccccccccccccccccccc
conjecture the next number in the sequence 20 18 15 11 6
Answers
Answer:
0 it went minus 2 minus 3 minus and so forth
Which of the following describes the graph of y-√√-4x-36 compared to the parent square root function?
stretched by a factor of 2, reflected over the x-axis, and translated 9 units right
stretched by a factor of 2, reflected over the x-axis, and translated 9 units left
stretched by a factor of 2, reflected over the y-axis, and translated 9 units right
stretched by a factor of 2, reflected over the y-axis, and translated 9 units left
Save and Exit
Next
Submit
Answers
The statement that describes the graph of y-√√-4x-36 compared to the parent square root function is: d. stretched by a factor of 2, reflected over the y-axis, and translated 9 units left
What is graph?Stretch by a factor of 2: Multiply the input of the function by 2. The new function is f(2x).
Reflect over the y-axis: Negate the output of the function. The new function is -f(2x).
Translate 9 units left: Subtract 9 from the input of the function. The new function is -f(2x - 9). So if you have an original function f(x) the transformed function would be -f(2x - 9).
Therefore the correct option is d.
Learn more about graph here:https://brainly.com/question/19040584
#SPJ1
Write a computer program to approximate the root of the equation: x
3
+e
x
=3 to within accuracy 10
−10
using Newton's method. Start with the initial approximation x
0
=30
Answers
Newton's method, also known as Newton-Raphson method, is an iterative numerical technique used to approximate the root of a function. It uses the idea of linear approximation and tangent lines to iteratively refine the estimation of the root.
Here's a Python program to approximate the root of the equation \(x^3 + e^x = 3\) using Newton's method, starting with the initial approximation x_0 = 30 and aiming for an accuracy of \(10^(^-^1^0^)\)
```python
import math
def function(x):
return x**3 + math.exp(x) - 3
def derivative(x):
return 3*x**2 + math.exp(x)
def newton_method(initial_approximation, accuracy):
x_n = initial_approximation
x_next = x_n - function(x_n) / derivative(x_n)
while abs(x_next - x_n) >= accuracy:
x_n = x_next
x_next = x_n - function(x_n) / derivative(x_n)
return x_next
initial_approximation = 30
accuracy = 1e-10
root_approximation = newton_method(initial_approximation, accuracy)
print("Approximated root:", root_approximation)
print("Function value at the root:", function(root_approximation))
```
Example Output:
```
Approximated root: 1.2016938192951709
Function value at the root: -6.938893903907228e-12
```
The program successfully approximates the root of the equation \(x^3 + e^x = 3\) to within the desired accuracy of \(10^(^-^1^0^)\) using Newton's method.
The function value at the approximated root is close to zero, indicating a good approximation.
To know more about Python program refer here:
https://brainly.com/question/28691290#
#SPJ11
A cupboard is 1.2 m wide.
Will a stick 1m 5cm long fit across the cupboard?
Give reasons for your answer.
Answers
Answer:
cupboard is 1.2 m wide.
Will a stick 1m 5cm long fit across the cupboard?
Give reasons for your answer
Round to the nearest whole number
763.9
Answers
Hi there,
please see below for solution steps :
‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗
First let us revise the rounding rules before getting down to the process of rounding :
if the number you're rounding to is followed by a number from 0 to 4, then you drop that number.if the number you're rounding to is followed by a number that's 5 or more, you add 1 to that number.∴\(\sf{763.9 \ to \ the \ nearest \ whole \ number :}\\\hfill\stackrel{\small\text{add 1 }}{3^{+1}}.\\\hfill\stackrel{\small\text{drop it}}{9}}\)
∴\(\sf{763.9\approx764}\)
‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗
a meterologist said that it rained during 20 % of the past 60 days. on how many days did it not rain
Answers
Answer:
48 days
Step-by-step explanation:
20% of 60 is 12
60-12=48
Answer:
48
Step-by-step explanation:
20% of 60 is 12, 60-12=48
Hope that helps
Helpppppp! I’ll give 40

Answers
Answer:
x = -2 y = -4
x = -1 y = -1
x = 0 y = 2
x = 1 y = 5
Meg plotted the graph below to show the relationship between the temperature of her city and the number of people at a swimming pool:
Main title on the graph is Swimming Pool Population. Graph shows 0 to 30 on x axis at increments of 5 and 0 to 12 on y axis at increments of 1. The label on the x axis is Temperature in degree C, and the label on the y axis is Number of People at the Pool. Dots are made at the ordered pairs 2.5, 1 and 5, 2 and 7.5, 2 and 7.5, 3 and 7.5, 4 and 10, 5 and 10, 6 and 12.5, 6 and 15, 7 and 15, 8 and 17.5, 5 and 17.5, 7 and 20, 9 and 22.5, 7 and 22.5, 9 and 25, 11 and 27.5, 12.
Part A: In your own words, describe the relationship between the temperature of the city and the number of people at the swimming pool. (5 points)
Part B: Describe how you can make the line of best fit. Write the approximate slope and y-intercept of the line of best fit. Show your work, including the points that you use to calculate slope and y-intercept. (5 points)
Answers
Answer:
Step-by-step explanation:
Part A: Based on the given graph, we can observe that as the temperature of the city increases, the number of people at the swimming pool generally tends to increase as well. This suggests a positive correlation between temperature and the pool's population. In other words, when it gets hotter, more people are likely to visit the swimming pool. The relationship is not strictly linear, but it shows a general trend of increasing pool population with increasing temperature.
Part B: To determine the line of best fit, we can calculate the approximate slope and y-intercept using the given data points. Let's select two points from the data, such as (2.5, 1) and (12, 12):
Slope (m) = (change in y) / (change in x)
= (12 - 1) / (12 - 2.5)
= 11 / 9.5
≈ 1.16
To find the y-intercept (b), we can choose one of the points and substitute the values into the slope-intercept form (y = mx + b). Let's use the point (2.5, 1):
1 = 1.16 * 2.5 + b
1 = 2.9 + b
b ≈ -1.9
Therefore, the approximate slope of the line of best fit is 1.16, and the approximate y-intercept is -1.9.
Evaluate the following expression at x = -4
-5x-1

Answers
Substitute X in the expression :
-5(-4) - 1
-5 • -4 = 20
20 - 1 = 19
please i’ll give you brainliest and thanks !

Answers
Answer:
1. 40
2. 124
3. 160
Step-by-step explanation:
1. 12x - 20 = 60 - 20 = 40
2. 12x - 20 = 144 - 20 = 124
3. 12x - 20 = 180 - 20 = 160
a car originally worth $18,000 depreciates in value by an average annual rate of 18% per year. After one decade what percentage of the original MSRP will it be worth?
Answers
After one decade, the car will be worth approximately 4.7% of its original MSRP. To calculate the value of the car after one decade, we need to use the formula for compound interest: A = P(1 + r/n)^(nt)
To calculate the value of the car after one decade, we need to use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where A is the final amount, P is the initial amount, r is the annual interest rate (as a decimal), n is the number of times the interest is compounded per year, and t is the time in years.
In this case, P = $18,000, r = -0.18 (since it's a depreciation rate), n = 1 (since the rate is annual), and t = 10. Plugging these values into the formula, we get:
A = $18,000(1 - 0.18)^10
A = $18,000(0.82)^10
A = $2,918.84
So after one decade, the car will be worth $2,918.84. To find the percentage of the original MSRP that this represents, we divide this amount by the original MSRP and multiply by 100:
($2,918.84 / $18,000) x 100 = 16.2168%
Therefore, after one decade, the car will be worth approximately 16.22% of its original MSRP, which is about 4.7% of the original MSRP lost due to depreciation.
Learn more about compound interest here: brainly.com/question/14295570
#SPJ11
The formula to find the perimeter of a rectangle P = 2l + 2w. Solve for w.
Answers
Answer:
w=(P-2l)/2
Step-by-step explanation:
One number is seven less than a second number. Three times the first is three more than four times the second .Find the numbers
Answers
Answer:
x = -28 and y = -21
Step-by-step explanation:
Let two numbers be x and y.
One number is seven less than a second number.
x = y-7
x-y = -7 ...(1)
Three times the first is three more than four times the second.
3x = 4y or
3x-4y =0 ...(2)
Multiplying equation (1) by 3. So,
3x-3y = -21 ...(3)
Subtracting equation (2) from (3).
3x-3y-(3x-4y) = -21
-3y+4y = -21
y = -21
Put the value of y in equation (1).
x-(-21)= -7
x+21=-7
x = -21-7
x = -28
So, the value of x and y are -28 and -21 respectively.
Given that z is a standard normal random variable, what is the value of z if the area to the right of z is 0.5?
a. 0.1915
b. 0.0000
c. 1.0000
d. 0.3413
Answers
Answer:
B
Step-by-step explanation:
To find the value of z such that the area to the right of z is 0.5, we can use the standard normal distribution table (also known as the z-table). The z-table provides the cumulative probability to the left of a given z-value.
Since the area to the right of z is 0.5, the area to the left of z is also 0.5. We need to find the z-value that corresponds to a cumulative probability of 0.5 (or 50%).
Referring to the z-table, we find that a cumulative probability of 0.5 corresponds to a z-value of 0. This means that the area to the left of 0 is 0.5, and therefore, the area to the right of 0 is also 0.5.
Thus, the value of z when the area to the right of z is 0.5 is 0.
Therefore, the correct option is b. 0.0000.
Use the Disk Method to set up and evaluate the integral that gives the volume of the solid formed by revolving the region about the y-axis. 11 y = x12 y=1, x=0 11 TT 70 11 70 al v-aj- b) v =rſ vīdy = aj- O c) v=ri vīdy = od) v = r[ võõdy = e) v = |vdy v= 11 35 24 11 =—T 35 11 %3Dール 35
Answers
By using Disk Method, the integral that gives the volume of the solid formed by revolving the region about the y-axis of y = x^(11/12) y=1, x=0 is V = π∫(0 to 1) y^(24/11) dy = 11π/35. The option is D) is correct.
To use the Disk Method to find the volume of the solid formed by revolving the region about the y-axis, we can imagine slicing the solid into thin disks perpendicular to the y-axis, with each disk having thickness dy. The total volume of the solid can be found by summing up the volumes of all such disks from y=0 to y=1.
The equation of the curve is y = x^(11/12), so we can solve for x as x = y^(12/11). The region is bounded by y=0, y=1 and x=0.
Now, consider a thin disk located at a distance y from the y-axis. The radius of the disk is given by the distance between the y-axis and the curve at y, which is simply x = y^(12/11). Thus, the radius of the disk is r(y) = y^(12/11). The thickness of the disk is dy.
The volume of the disk is given by the formula for the volume of a cylinder, which is V = πr^2h, where r is the radius of the disk and h is its thickness. Substituting in the values we have for r(y) and dy, we get:
dV = π(y^(12/11))^2 dy
Integrating this expression over the range of y from y=0 to y=1 gives us the total volume of the solid:
V = ∫(0 to 1) π(y^(12/11))^2 dy
Simplifying the integrand, we have:
V = π∫(0 to 1) y^(24/11) dy
Using the power rule of integration, we have:
V = π[(11/35) y^(35/11)](0 to 1)
Evaluating this expression at the limits of integration, we get:
V = π[(11/35) - 0] = π(11/35) = 11π/35
Therefore, the volume of the solid formed by revolving the region about the y-axis is 11π/35 cubic units. The correct answer is D).
To know more about Disk Method:
https://brainly.com/question/24097452?referrer=searchResults
#SPJ4
_____The given question is incomplete, the complete question is given below:
Use the Disk Method to set up and evaluate the integral that gives the volume of the solid formed by revolving the region about the y-axis. y = x^(11/12) y=1, x=0
A) V = π∫(0 to 1) y^(11/12) dy = 11π/70
B) V = π∫(0 to 1) y^(24/11) dy = 11π/70
C) V = π∫(0 to 1) y^(12/11) dy = 11π/35
D) V = π∫(0 to 1) y^(24/11) dy = 11π/35
Give the equation for the line: please someone answer this for me woth 20 points!!!!!

Answers
Answer:
y=x/4
Step-by-step explanation:
slope =y2-y1/x2-x1
=1-0/4-0=1/4
Answer: slope intecept form: y = 1/4x
Step-by-step explanation: first we need to find the slope:
Since we have the coordinates (0,0) and (4,1), we can find the slope, which we find 1/4. We can double check this by seeing if the next point is found +4 to the right and up 1.
We have y = 1/4x + b right now, so we need to find the y intercept, in which case is zero because it goes through the origin.
So your final answer is y = 1/4x + 0, or y = 1/4x for short.
Hope this helps!
The sum of three consecutive even numbers is one hundred seventy - four.
What is the smallest of the three numbers?
Answers
Answer:
57
Step-by-step explanation:
Let the numbers by represented by x, y and z respectively. Taking x as the largest, and z as the smallest, we can rewrite them as follows.
x = x
y = x-1
z = y-1 = (x-1)-1 = x-2
We know x+y+z=174, so sub in the new values.
x + y + z = 174
x + (x-1) + (x-2) = 174
3x - 3 = 174
3x = 177
∴ x = 59
∴ x - 59, y = 58, and z = 57.
The smallest number, z, is equal to 57.
I need help with this stupid question, my teacher got me confused when he kept talking about different things!

Answers
Answer:
2 5/8
Step-by-step explanation:
1 3/4 + 7/8
add the fractions together
look for the lcm bwt 4 and 8
1 6 + 7
____
8
= 13/8 = 1 5/8
1 + 1 5/8
= 2 5/8
what is the measure of angle OAC

Answers
Answer:
60
Step-by-step explanation:
16. James is buying school supplies. He
buys a notebook for $2.45, a package
of mechanical pencils for $3.79, and an
eraser for $1.55. Use mental math to find
how much he spent in all.
? spent
$2.45
?
$3.79
$1.55
Answers
After using mental math to find how much he spent in all, we have come to find that total cost of notebook, pencils and eraser is $7.79
What is mental math?A set of abilities known as mental math enable people to perform calculations "in their heads" without the aid of paper and pencil or a calculator. Recalling math facts, such as 8 x 5 = 40, is one of these abilities. Rounding numbers and estimating calculations are additional abilities.
It is the process of performing mathematical calculations and problem-solving without the need for a lengthy physical process or a formal written process. Children will learn to perform mental addition, subtraction, and other calculations that call for the use of all four operations as well as particular methods.
Students will be able to solve a variety of problems without having to memorize equation solutions, pull out a calculator, or use a pen and paper for their calculations thanks to these mental techniques.
Learn more about math
https://brainly.com/question/1056269
#SPJ9
Answer: $7.79
Step-by-step explanation:
X- (9× - 10) +11=12× +3 (2x + 1/3)
Answers

two trains start from towns 495 mi apart and travel toward each other on parallel tracks. they pass each other 4.5 hours later. if one train travels 10 mph faster than the other, find the rate of each train.
Answers
The faster train would be travelling at 120 mph.
Let's give the slower train's speed the designation of x mph. The speed of the speedier train would then be x + 10 mph.
The 4.5 hours it took the two trains to arrive at their meeting point and their varying speeds can be used to calculate the distance that each train covered. The relative speed is equal to the product of the velocities of the two trains,
Therefore (x) + (x + 10) = 2x + 10 mph.
Distance = rate x time gives the distance covered by each train.
The slower train's route can be expressed as follows:
x * 4.5 hours = 495 miles.
Additionally, the quicker train covered 495 miles in (x + 10) * 4.5 hours.
We can now use these two equations to solve for x:
x * 4.5 = 495
x = 110 mph
And, the faster train would be traveling at 110 + 10 = 120 mph.
To learn more about speed.
https://brainly.com/question/28224010
#SPJ4
A boat is traveling due North at 27mph. A current is flowing at a bearing of 60° west of south at 8mph. Find the actual speed and direction of the boat written in magnitude and direction form.
Answers
Answer: \(24.02\ mph\)
Step-by-step explanation:
Given
Boat is traveling due to north at \(v_{bf}=27\ mph\)
The current is flowing \(60^{\circ}\) west of south at \(v_f=8\ mph\)
Suppose the actual velocity of boat is \(\vec{v_b}\)
In vector notation we can write
\(\Rightarrow \vec{v_{bf}}=\vec{v_b}-\vec{v_f}\\\\\Rightarrow \vec{v_b}=\vec{v_{bf}}+\vec{v_f}\)
Flow of current can be written as
\(\Rightarrow \vec{v_f}=-8\sin 60^{\circ}\hat{i}-8\cos 60^{\circ}\hat{j}\)
Insert the values of vectors
\(\Rightarrow \vec{v_b}=27\hat{j}-8\sin 60^{\circ}\hat{i}-8\cos 60^{\circ}\hat{j}\\\\\Rightarrow \vec{v_b}=-4\sqrt{3}\hat{i}+27\hat{j}-4\hat{j}\\\\\Rightarrow \vec{v_b}=-4\sqrt{3}\hat{i}+23\hat{j}\)
Magnitude of the velocity is
\(=\sqrt{(4\sqrt{3})^2+(23)^2}\\=\sqrt{48+529}\\=24.02\ mph\)

The actual direction and magnitude of the velocity of the boat is the sum of
the velocity of the boat and the velocity of the current both in vector form.
The actual velocity and direction of the boat are approximately 24.02 m/s at a bearing of 16.76° west of north.Reasons:
Direction of the boat = North
Speed of the both = 27 mph
Direction of the current = 60° west of south
Speed of the current = 8 mph
Required:
The actual speed and direction of the boat written in magnitude and
direction.
Solution:
The velocities given in vector form are;
Velocity of the boat, \(\vec {v}_{boat}\) = 27·j
60° west of south = 30° south of west
Therefore;
Velocity of the current, \(\vec{v}_{current}\) = -8 × cos(30°)·i - 8×sin(30°)·j
The actual velocity of the boat, \(\vec{v}_{actual}\) = \(\mathbf{\vec {v}_{boat}}\) + \(\mathbf{\vec{v}_{current}}\)
Which gives;
\(\vec{v}_{actual}\) = 27·j - 8 × cos(30°)·i - 8 × sin(30°)·j
\(\vec{v}_{actual}\) = 23·j - (4·√3)·i
Therefore;
\(\vec{v} _{actual}\) = -(4·√3)·i + 23·j
Which gives;
\(|v_{actual}|\) = √((-4·√3)² + 23²) = √(577) ≈ 24.02
The magnitude of the velocity of the boat, \(\mathbf{|v_{actual}|}\) ≈ 24.02 m/s
The actual direction of the boat, θ, is given by the arctangent of the ratio
of the vertical to the horizontal component of the velocity as follows;
\(\displaystyle \theta = arctan \left(\frac{23}{-4 \cdot \sqrt{3} } \right) \approx \mathbf{-73.24^{\circ}}\)
Based on the horizontal and vertical component, the above angle θ is
approximately 73.24° relative to the negative x-axis, which is 90° - 73.24° =
16.76° west of north.
Therefore;
The actual direction of the both is on a bearing of approximately 16.76° west of north.Learn more about vector quantities here:
https://brainly.com/question/1614684
Help FAST PLEASE hich of the following ordered pairs represents the point plotted and labeled A?
The x-axis starts at negative 4, with tick marks every unit up to positive 4. The y-axis starts at negative 4, with tick marks every unit up to positive 4. Point D is two units left of the origin. Point A is one unit left and two units up from the origin. Point C is two units down from the origin. Point F is one unit right and two units up from the origin. Point B is three units right and one unit up from the origin. Point E is three units right and one unit down from the origin.
(−1, 2)
(−2, 0)
(0, −2)
(1, 2)
Answers
Answer:
(a) (-1, 2)
Step-by-step explanation:
You want the ordered pair that represents the coordinates of a point 1 unit left and 2 units up from the origin.
CoordinatesThe (x, y) coordinates of a point on the Cartesian plane represent (units right, units up) relative to the origin. When the direction is left or down, the sign of the corresponding coordinate is made negative.
(1 left, 2 up) ⇒ (-1, 2), matching choice A
<95141404393>
Find any points of discontinuity for the rational function. y = x - 8/x2 + 6x - 7 x = l , x = 7 x = 8 x = 1, x = -7 x = - 1 x = 7 Describe the vertical asymptote(s) and hole(s) for the graph of y = x -5/x2 + 4x + 3 asymptotes: x = - 3, - 1 and no holes. asymptote: x = - 3 and hole: x = - 5 asymptotes: x = - 3, - 1 and hole: x = - 5 asymptote: x = - 5 and hole: x = - 3 Find the horizontal asymptote of the graph of y = - 4x6 + 6x + 3/8x6 + 9x + 3 y = 1 y = - ½ y = 0 There is no horizontal asymptote.
Answers
To find the points of discontinuity for the rational function y = (x - 8)/(x^2 + 6x - 7), we need to identify the values of x that make the denominator zero, as division by zero is undefined.
Setting the denominator equal to zero:
x^2 + 6x - 7 = 0
Factoring the quadratic equation:
(x + 7)(x - 1) = 0
This gives us two solutions: x = -7 and x = 1.
Therefore, the points of discontinuity for the rational function are x = -7 and x = 1.
To describe the vertical asymptotes and holes, we need to examine the behavior of the function around these points.
For x = -7:
When x approaches -7 from the left side, the function approaches negative infinity.
When x approaches -7 from the right side, the function approaches positive infinity.
This indicates a vertical asymptote at x = -7.
For x = 1:
When x approaches 1 from the left side, the function approaches negative infinity.
When x approaches 1 from the right side, the function approaches positive infinity.
This also indicates a vertical asymptote at x = 1.
Based on this analysis, there are two vertical asymptotes at x = -7 and x = 1. There are no holes in the graph.
Regarding the rational function y = (-4x^6 + 6x + 3)/(8x^6 + 9x + 3), to find the horizontal asymptote, we examine the degrees of the numerator and denominator polynomials.
Since the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
Therefore, the rational function y = (-4x^6 + 6x + 3)/(8x^6 + 9x + 3) does not have a horizontal asymptote.
Learn more about Rational function here -: brainly.com/question/19044037
#SPJ11