Sharia surveyed students and teachers to determine how long it takes each person, in minutes, to get ready for school in the morning. The plots below show the results of the survey. Which statements accurately compare the two data sets? Select three options
Answers
Answer:
B),D),E)
Step-by-step explanation:
Trust
Answer:
B,D,E
Step-by-step explanation:
I got it correct on the quiz
Related Questions
At any time t > 0,the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized ad tlie number of words tlat have not been memorized. If 2 denotes the number of words memorized at time t, which differential equation models this situation? Assume kis a positive constant; A. d k dt B. d k ( - M) dt C d k(M - 2) dt D. d =Rt(M -t) dt
Answers
The differential equation that models this situation is dx/dt = kx(M - x) (option c).
To determine the differential equation that models the situation, let's analyze the problem statement.
The rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized.
Let's denote the number of words memorized as "a" and the number of words not yet memorized as "M - a" (where M is the total number of words in the list).
The problem states that the rate of memorization is proportional to the product of "a" and "M - a". We can express this mathematically as:
Rate of memorization ∝ a * (M - a)
To convert this proportionality into an equation, we introduce a positive constant k:
Rate of memorization = k * a * (M - a)
The left side of the equation represents the rate of change of the number of words memorized (da/dt), and the right side represents the product of "a" and "M - a" multiplied by the constant k.
Therefore, the differential equation that models this situation is:
da/dt = k * a * (M - a)
Comparing this with the given options, we can see that the correct choice is option C:
dx/dt = k * x * (M - x)
The complete question is:
At any time t > 0 the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized. If a denotes the number of words memorized at time t, which differential equation models this situation? Assume k is a positive constant.
A. dx/dt = kx
B. dx/dt = kx(x - M)
C. dx/dt = kx(M - x)
D. dx/dt = kt(M - t)
To know more about differential equation:
https://brainly.com/question/32524608
#SPJ4
What is the perimeter of this 48" by 60" rug?
Answers
Given f(x) = x − 7 and g(x) = x2 Find f(g(4)).
Answers
Answer:
1
Step-by-step explanation:
First we can solve for \(g(x) = 2x\) where \(x = 4\) so we get: \(g(4) = 8\).
Then we put that into the \(f(x) = x - 7\). So we now have: \(f(8) = 8 - 7 = 1\)
Answer:
9
Step-by-step explanation:
Ok so if g(x) is 2x, then I'm wrong, but if it's x squared then look below:
Since there is a 4 instead of a x in g(x), we would substitute x=4 into g(x) so:
g(x) = x^2
g(4) = 4^2
g(4) = 16
Now we would substitute x=16 into f(x):
f(x) = x - 7
f(16) = 16 - 7
f(16) = 9
So f(g(4)) is 9.
2. The local Farm Market sells peppers at five for $2.25. Complete the rate table Number of Peppers 1 2 4 5 10 15 20 100 Cost 2.25 What is the constant of proportionality? How do you know?
Answers
Answer:
K = $0.45
1____ 2__ 4 __5___10__ 15__ 20__ 100
0.45_0.9_1.8_2.25_4.5_6.75__9___45
Step-by-step explanation:
Given the data:
Number of pepper: 1 2 4 5 10 15 20 100
Cost :
Cost of 5 pepper = 2.25
Using variation :
Cost = number of pepper * k
K = CONSTANT of proportionality
k = cost / number of pepper
k = 2.25 / 5
k = 0.45
Hence,
Cost of pepper = k * number of pepper
Number of pepper:
Cost :
1____ 2__ 4 __5___10__ 15__ 20__ 100
0.45_0.9_1.8_2.25_4.5_6.75__9___45
-5n = 20
Help don’t have time
Answers
Answer:
n= -4
Step-by-step explanation:
Divide by -5 on both sides, regularly, 20/5 is equal to 4 so basically all youre doing is making it -4. Hope this helps :)
-5n=20
-4
I belive........
Find the measure of Tu in the photo

Answers
The value of the tangent TU for the circle with secant through U which intersect the circle at points V and W is equal to 12
What are circle theoremsCircle theorems are a set of rules that apply to circles and their constituent parts, such as chords, tangents, secants, and arcs. These rules describe the relationships between the different parts of a circle and can be used to solve problems involving circles.
For the tangent TU and the secant through U which intersect the circle at points V and W;
TU² = UV × VW {secant tangent segments}
(5x)² = 9 × 16
(5x)² = 144
5x = √144 {take square root of both sides}
5x = 12
x = 12/5
so;
TU = 5(12/5)
TU = 12
Therefore, the value of the tangent TU for the circle with secant through U which intersect the circle at points V and W is equal to 12
Read more about circle here:https://brainly.com/question/17023621
#SPJ1
3. Josh rode his bike at a constant speed. He rode 1 miles in 7 minutes.
Josh rode his bike at a constant speed he rode 1 miles in 7 minutes Which of these equations represents the amount of time (in minutes) that it takes him to
ride a distance of miles?
a. d = 1/7 xt
b. t = 7 d
c. t = d + 6
d. t= d - 6

Answers
Answer:
Step-by-step explanation:
Andre rode his bike at a constant speed. Time taken to drive 1 mile = 7 minutes. Now we have to find the amount of time t (in minutes) taken by him to right distance so we can again use same formula.
Hence find answer will be equation;
t=5d
The legs of the base of a right triangular
prism measure 9 in. and 12 in. The prism has
a height of 5 in. What is the surface area of
the prism?

Answers
Answer:
the surface area of the prism = 288 in²Step-by-step explanation:
Let S be the surface area of the prism
B be the area the base (right-angered triangle)
L be the lateral surface area
Formula :
S = 2×B + L
……………………
\(B=\frac{12\times 9}{2} = 54\)
\(\text{Length \ of \ the \ third \ side}=\sqrt{12^{2}+9^{2}} =15\)
L = 5×(9 + 12 + 15) = 180
S = 2×B + L
S = 2×54+180 = 288 in²
Let R denote the ring Z[i]/(1+3i).(i) Show that i-3 € (1+36) and that [i] = [3] in R. Use this to prove that [10][0] in R and that [a+bi] = [a+3b], where a, b Z.(ii) Show that the unique ring homomorphism6: Z→ Ris surjective.(iii) Show that 1+3i is not a unit and that 1+3i does not divide 2 and 5 in Z[]. Conclude that Ker() = 102.(iv) Show that RZ/10Z
Answers
(i) As we have proved that [10][0] in R and that [a+bi] = [a+3b], where a, b Z.
(ii) As we have proved that the unique ring homomorphism 6: Z→ Ris surjective
(iii) As we have proved that 1+3i is not a unit and that 1+3i does not divide 2 and 5 in Z[].
(iv) We can then show that Ker(ψ) = 10Z in R, which is the ideal generated by 10 in R.
(i) The first part of the problem asks us to show that i-3 € (1+36) and that [i] = [3] in R. To do this, we need to understand what R represents. R is the ring obtained by taking the quotient of the ring of Gaussian integers Z[i] by the ideal generated by 1+3i. In other words, we consider all the possible integers in Z[i], but we identify any two integers that differ by a multiple of 1+3i. So, [i] represents the equivalence class of all the integers in Z[i] that are equivalent to i modulo 1+3i.
Finally, we can use the fact that [a+bi] = [a+3b] in R for any integers a and b. To see this, note that [a+bi] = [(a-3b) + (b+3a)i], which is equivalent to [a+3b] modulo 1+3i. Therefore, we have [a+bi] = [a+3b] in R.
(ii) The second part of the problem asks us to show that the unique ring homomorphism Φ: Z → R is surjective. In other words, every element of R is the image of some integer in Z under Φ.
Now, let [a+bi] be an arbitrary element of R. We need to show that there exists an integer n such that Φ(n) = [a+bi]. To do this, note that [a+bi] = [(a-3b) + (b+3a)i], which is equivalent to (a-3b) modulo 1+3i. Therefore, we can choose n = a-3b, and we have Φ(n) = [n] = [a+bi]. This shows that Φ is surjective.
(iii) The third part of the problem asks us to show that 1+3i is not a unit in R and that 1+3i does not divide 2 and 5 in Z[i]. We then need to use these facts to conclude that Ker(Φ) = 102, which is the kernel of the homomorphism Φ.
To show that 1+3i is not a unit in R, we need to show that there is no element in R that, when multiplied by 1+3i, gives the multiplicative identity in R. Suppose, for the sake of contradiction, that there exists such an element [a+bi] in R. This means that (1+3i)(a+bi) is equivalent to 1 modulo 1+3i, which implies that 3a+b is a multiple of 1+3i. But this is not possible, since 1+3i is not a divisor of any integer of the form 3a+b in Z[i]. Therefore, 1+3i is not a unit in R.
(iv) The final part of the problem asks us to show that RZ/10Z, which is the quotient of R by the ideal generated by 10 in Z[i], is isomorphic to the ring Z/10Z. To do this, we can define a ring homomorphism ψ: R → Z/10Z by ψ([a+bi]) = a mod 10, which maps each equivalence class in R to its residue modulo 10 in Z/10Z.
To know more about homomorphism here
https://brainly.com/question/6111672
#SPJ4
a,b,c,or d !? please help

Answers
Answer:
b
Step-by-step explanation:
A boat is carrying containers that weigh 4000 pounds each.
Use this information to fill in the table. Then plot the ordered pairs given by the table.
Answers
By applying direct proportion, the information should be filled in the table are as follows:
Number of containers Weight (in pounds)
4 16,000
8 32,000
10 40,000
What is a proportion?A proportion can be defined as an equation which is typically used to represent (indicate) the equality of two (2) ratios. This ultimately implies that, proportions can be used to establish that two (2) ratios are equivalent and solve for all unknown quantities.
Mathematically, a direct proportion can be represented the following equation:
y = kx
Where:
y and x are the variables.k represents the constant of proportionality.Since the boat carried containers that weigh 4000 pounds each, we would multiply each of containers by 4000 as follows:
Number of containers Weight (in pounds)
4 16,000
8 32,000
10 40,000
Read more on proportionality here: https://brainly.com/question/12866878
#SPJ1


solve the quadratic equation 3x squared plus x minus 5 equals 0
Answers
To solve the quadratic equation 3x² + x - 5 = 0, we can use the quadratic formula:
What is quadratic equation?A quadratic equation is a type of equation in algebra that involves a single variable (usually x) raised to the second power, or a multiple of x². The general form of a quadratic equation is:
ax² + bx + c = 0
where a, b, and c are constants (numbers), and x is the variable.
The quadratic equation is important in mathematics and science because it appears in many real-world applications, such as physics, engineering, and economics. It is also used to model many types of natural phenomena, such as the trajectory of a ball thrown into the air, the shape of a parabolic dish, or the behavior of a vibrating string.
Solving quadratic equations involves finding the values of x that make the equation true. This can be done using a variety of methods, including factoring, completing the square, and using the quadratic formula. The solutions to a quadratic equation can be real (meaning they are numbers that can be plotted on a number line) or imaginary (meaning they involve the square root of a negative number).
x = (-b ± √(b² - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
In this case, a = 3, b = 1, and c = -5, so we can substitute these values into the formula and simplify:
x = (-1 ± √(1² - 4(3)(-5))) / 2(3)
x = (-1 ± √(61)) / 6
Therefore, the solutions to the quadratic equation are:
x = (-1 + √(61)) / 6 or x = (-1 - √(61)) / 6
These are the exact solutions, but if we want to approximate them to a certain number of decimal places, we can use a calculator. For example, to approximate the solutions to two decimal places, we get:
x ≈ 0.81 or x ≈ -1.48
Therefore, the solutions to the quadratic equation 3x² + x - 5 = 0 are approximately x = 0.81 and x = -1.48.
Learn more about quadratic equation
https://brainly.com/question/1214333
#SPJ1
company a rents copiers for a monthly charge of $200 plus 10 cents per copy. company b rents copiers for a monthly charge of $400 plus 5 cents per copy. what is the number of copies above which company a's charges are the higher of the two? write your answer as a number only.
Answers
Therefore, when the number of copies made in a month is above 4000, company A's charges are higher than company B's charges in the given equation.
Let's start by setting up an equation to represent the cost of renting a copier from each company:
Cost for company A = 0.10x + 200
Cost for company B = 0.05x + 400
where x is the number of copies made in a month.
To find the number of copies above which company A's charges are higher than company B's charges, we need to set the two equations equal to each other and solve for x:
0.10x + 200 = 0.05x + 400
0.05x = 200
x = 4000
To know more about equation,
https://brainly.com/question/28243079
#SPJ11
To solve the system of linear equations 3 x minus 2 y = 4 and 9 x minus 6 y = 12 by using the linear combination method, Henry decided that he should first multiply the first equation by –3 and then add the two equations together to eliminate the x-terms. When he did so, he also eliminated the y-terms and got the equation 0 = 0, so he thought that the system of equations must have an infinite number of solutions. To check his answer, he graphed the equations 3 x minus 2 y = 4 and 9 x minus 6 y = 12 with his graphing calculator, but he could only see one line. Why is this?
Answers
Henry could only see one line since both lines had the same slope, which means that the graphs of both equations will be identical and hence overlap.
Identify the linear equation?Linear equations in a system 3x + 2y = 4, and 9x + 6y = 12
We must demonstrate why Henry could only make out one line when he plotted the equations 3x-2y=4 and 9x-6y=12 on a graph.
Take the provided linear equation system into consideration.
3x - 2y = 4 ................(1)
9x - 6y = 12 ..................(2)
Due to the fact that equation (2) is a multiple of equation (1), 3 (3x - 2y = 4) = 9x - 6y = 12
The slopes of the provided equations are also same.
Difference with regard to x for equation (1) yields,
additional to equation (2),
With regard to x, we can differentiate to get,
The graphs of both equations will overlap since both lines have the same slope and hence have the same appearance on the graph.
To learn more about linear equations refer to:
https://brainly.com/question/2030026
#SPJ1
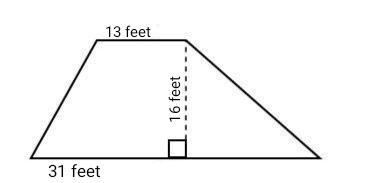
What is the area of this trapezoid? Enter your answer in the box. Ft²
Trapezoid with parallel sides labeled 13 feet and 31 feet. The dashed perpendicular
segment between them is labeled 16 feet
Answers
The area of the given trapezoid would be 176 feet² with the length of the parallel sides of the trapezoid is 13 feet and 31 feet respectively and the height of the trapezoid given is 16 feet.
Given that,
The length of the parallel sides of the trapezoid is 13 feet and 31 feet
The height of the trapezoid given is 16 feet.
We know that area of trapezoid is (a+b)×h/2
Where, (a) and (b) are Length of the parallel sides of trapezoid and h is the height of trapezoid.
Thus, Area = (13+31) × 16/2
Area = 22×8
Area = 176 feet²
Hence the area of the given trapezoid would be 176 feet² with the length of the parallel sides of the trapezoid is 13 feet and 31 feet respectively and the height of the trapezoid given is 16 feet.
Visit here to learn more about the area: https://brainly.com/question/27683633
#SPJ4
You can replace the values in a problem with
___________ so that it's easier to use mental
math to complete the computation.
Answers
You can replace the values in a problem with letters or words so that it's easier to use mental math to complete the computation.
This is further explained below.
What are letters or words?Generally, A word may also refer to both a string of letters that are denoted by a certain meaning and the space that separates those characters from one another.
A graphic representation of a spoken sound is often written or printed and is the basic building block of an alphabet.
In conclusion, You may make it simpler to compute using mental math by changing the numbers in a problem to letters or words, which will make it possible for you to solve the issue more quickly.
Read more about letters
https://brainly.com/question/5395395
#SPJ1
is the standard deviation of the numbers x, y, and z equal to the standard deviation of 10, 15, and 20 ?
Answers
This matches the placement of 10, 15, and 20 and hence the standard deviation will be the same in the two cases.
What is the standard deviation?
The standard deviation in statistics is a measure of the amount of variation or dispersion in a set of values. A low standard deviation indicates that the values are close to the set's mean, whereas a high standard deviation indicates that the values are spread out over a wider range.
Standard deviation determines how far numbers deviate from the mean. The Standard deviation of the two sets will be the same if the numbers from the respective means are placed in the same order.
This is what 10, 15, and 20 will be on a number line
10_ _ _ _15 _ _ _ _20
(15 is the mean and 10 and 20 are 5 steps away from the mean)
i) Z - X = 10
This is what Z and X will be on the number line
X _ _ _ _ _ Z
ii) Z - Y = 5
This is what Z and Y will on the number line.
Y_ _ _ _ _ Z
Together, their relative placement on the number line:
X _ _ _ _ _ Y _ _ _ _ _ Z
This matches the placement of 10, 15, and 20 and hence the standard deviation will be the same in the two cases.
To learn more about the area of the standard deviation visit,
https://brainly.com/question/475676
#SPJ1
Identify next three numbers in this sequence: 3, 12, 6, 24, 18, … 27, 13.5, 22.5 72, 66, 264 72, 36, 144 27, 21, 30
Answers
Answer:
its 72, 36, 144
Step-by-step explanation:
yes it is!!!
Which ordered pair makes the equation y = 4 x + 21 true?
Answers
Answer: x=
1
4
y+
−21
4
Step-by-step explanation:
Let's solve for x.
y=4x+21
Step 1: Flip the equation.
4x+21=y
Step 2: Add -21 to both sides.
4x+21+−21=y+−21
4x=y−21
Step 3: Divide both sides by 4.
4x
4
=
y−21
4
x=
1
4
y+
−21
4
Identify the type of data (qualitative/quantitative) and the level of measurement for the eye color of survet respondents.
Answers
Qualitative data depicts qualities or characteristics. This type of data is qualitative and nominal.
What is qualitative data?Qualitative data are the conceptual and descriptive findings gathered by surveys, interviews, or observation. We can explore concepts and provide more context for quantitative findings by analyzing qualitative data.
Qualitative data exist as measures of "types" and can be represented by a name, symbol, or number code, whereas quantitative data exist as information on numerical variables (such as how many, how much, or how frequently).
Numbers are used to expressing measures of values or counts in quantitative data. Binary, nominal, and ordinal are the three primary forms of qualitative data.
Qualitative data comes in a wide variety of forms, including those used in statistics, work, and research. This type of data is qualitative and nominal.
To learn more about qualitative data, refer to:
https://brainly.com/question/24492737
#SPJ4
which scatterplot has a correlation coefficient close to 0 but also has a strong relationship between the variables?
Answers
A scatterplot with a strong nonlinear relationship can have a correlation coefficient close to 0, but still have a strong relationship between the variables.
For example, consider a scatterplot where the points follow a curved pattern, such as a parabola or a sine wave. In such a case, the correlation coefficient may be close to 0, indicating no linear relationship between the variables, but there is still a strong nonlinear relationship between them.
In general, it is important to consider the shape and pattern of the scatterplot, in addition to the correlation coefficient, when assessing the relationship between two variables. A scatterplot with a weak correlation coefficient and a random scatter of points may indicate no relationship, while a scatterplot with a strong nonlinear pattern may indicate a strong relationship, even if the correlation coefficient is close to 0.
Learn more about scatterplot here:
https://brainly.com/question/29366075
#SPJ11
below are two parallel lines with a third line intersecting them.

Answers
136 is your answer. you can also see that 44 degrees is on a straight line so you can do 180 ( because a straight line is 180 degrees) minus 44 which also gives you 136
7-12 find the limit.
8. \(\lim _{t \rightarrow \infty} \frac{t^{3}-t+2}{(2 t-1)\left(t^{2}+t+1\right)}\)
Answers
Divide through the limand by the highest power of t :
\(\displaystyle \lim_{t\to\infty} \frac{t^3-t+2}{(2t-1)(t^2+t+1)} = \lim_{t\to\infty} \frac{1 - \frac1{t^2} + \frac2{t^3}}{\left(2-\frac1t\right) \left(1+\frac1t + \frac1{t^2}\right)}\)
(I distributed 1/t³ in the denominator as 1/t (2t - 1) and 1/t² (t² + t + 1).)
As to goes to infinity, these 1/tⁿ terms will converge to 0, and you're left with
\(\displaystyle \lim_{t\to\infty} \frac{1 - \frac1{t^2} + \frac2{t^3}}{\left(2-\frac1t\right) \left(1+\frac1t + \frac1{t^2}\right)} = \frac{1 - 0 + 0}{(2-0)(1+0+0)} = \boxed{\frac12}\)
what is the slope intercept form of the equation 15x-4y=32
Answers
Answer: y = 15/4 x - 8
Step-by-step explanation:
Find the midpoint of the segment ending in the points (0, 9) and (5, 1).
Answers
Answer:
(5/2,5)
Step-by-step explanation:
Let G be a group and let a and b be two elements in G. Suppose n is a positive integer. Compute (aba-1)^n. proof by induction
Answers
To compute the expression (aba⁻¹)^n using induction, we will prove the result for the base case (n = 1) and then show that if the statement holds for n = k, it also holds for n = k + 1.
Base Case (n = 1):
Consider (aba⁻¹)^1. Since any element raised to the power of 1 is itself, we have:
(aba⁻¹)^1 = aba⁻¹
Inductive Step:
Assume that for some positive integer k, (aba⁻¹)^k = ab^ka⁻¹ holds true.
Now, we will prove that (aba⁻¹)^(k + 1) = ab^(k+1)a⁻¹.
Using the assumption, we have:
(aba⁻¹)^(k + 1) = (aba⁻¹)^k * (aba⁻¹)
Using the associative property of the group operation, we can rearrange the terms:
(aba⁻¹)^(k + 1) = ab^ka⁻¹ * aba⁻¹
Now, we can group the terms:
(aba⁻¹)^(k + 1) = ab^k(a⁻¹a)ba⁻¹
Since a⁻¹a is the identity element (e) of the group G, we have:
(aba⁻¹)^(k + 1) = ab^keba⁻¹
Since b^k is a constant, we can write it as (b^k)e:
(aba⁻¹)^(k + 1) = ab^keba⁻¹ = ab^ke(ba⁻¹a⁻¹)aa⁻¹
Using the associative property again, we can rearrange the terms:
(aba⁻¹)^(k + 1) = ab^ke(ba⁻¹)(a⁻¹a)a⁻¹
As (a⁻¹a) and (a⁻¹a⁻¹) are both equal to the identity element (e), we have:
(aba⁻¹)^(k + 1) = ab^ke(ba⁻¹)(a⁻¹a)a⁻¹ = ab^kea⁻¹
Finally, substituting b^k with its equivalent (b^k)e, we get:
(aba⁻¹)^(k + 1) = ab^kea⁻¹ = ab^(k+1)a⁻¹
This completes the inductive step.
By proving the base case and showing that if the statement holds for n = k, it also holds for n = k + 1, we have proven by induction that (aba⁻¹)^n = ab^na⁻¹ for any positive integer n.
Learn more about induction here
https://brainly.com/question/29503103
#SPJ11
Find a linear function h given h(-1)=-2 and h(-7)=-9 The linear function is h(x)= (Simplify your answer. Use integers or fractions for any numbers in the expression.)
Answers
h(x) = -7/6x - 25/6.
Given h(-1)=-2 and h(-7)=-9
For linear function h(x), we can use slope-intercept form which is y = mx + b, where m is the slope and b is the y-intercept.
To find m, we can use the formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
h(-1) = -2 is a point on the line, so we can write it as (-1, -2).
h(-7) = -9 is another point on the line, so we can write it as (-7, -9).
Now we can find m using these points: m = (-9 - (-2)) / (-7 - (-1)) = (-9 + 2) / (-7 + 1) = -7/6
Now we can find b using one of the points and m. Let's use (-1, -2):
y = mx + b-2 = (-7/6)(-1) + b-2 = 7/6 + b
b = -25/6
Therefore, the linear function h(x) is:h(x) = -7/6x - 25/6
We can check our answer by plugging in the two given points:
h(-1) = (-7/6)(-1) - 25/6 = -2h(-7) = (-7/6)(-7) - 25/6 = -9
The answer is h(x) = -7/6x - 25/6.
Know more about linear function here,
https://brainly.com/question/29205018
#SPJ11
What is the mathematical model of an AST for a BL statement?
Answers
The mathematical model of an abstract syntax tree (AST) for a programming language's block (BL) statement typically involves representing the syntax of the statement using a tree structure.
This tree structure consists of nodes that correspond to different components of the statement, such as keywords, variables, operators, and expressions. The AST provides a way to parse and interpret the syntax of the statement, allowing for efficient compilation and execution of the code.
The model can be represented using various algorithms and data structures, such as recursive descent parsing or top-down parsing. Ultimately, the AST serves as a tool for developers to analyze, optimize, and debug their code, and is an essential component of many modern programming languages.
Learn more about syntax:
https://brainly.com/question/21926388
#SPJ11
f(x)=x², g(x)=2x²
The points (-1, 1), (0, 0), and (1, 1) of f(x) translate to the points ‘blank’ of g(x).

Answers
The coordinate points of g(x) are (-1, 2), (0, 0), (1, 2).
Which are the coordinates of the new points?
We know that the points (-1, 1), (0, 0), and (1, 1) belong to f(x) graph, where:
f(x) = x^2
Notice that the inputs in these points are x = -1, x = 0, x = 1.
Function g(x) is:
g(x) = 2x^2
Using the given inputs, we have:
g( -1) = 2*(-1)^2 = 2
g(0) = 2*0^2 = 0
g(1) = 2*(1)^2 = 2
Then the coordinate points of g(x) are (-1, 2), (0, 0), (1, 2).
Learn more about coordinate points:
https://brainly.com/question/12959377
#SPJ1
The measure of two complementary angle are (2x+2)degrees and (3x-5) degrees. What is measure of smaller angle?
Answers
so the two angles add to 90.
(2x+2) + (3x-5) = 90
5x - 3 = 90
5x = 93
x = 18.6
now plug that into both, you’ll get:
(2(18.6)+2) = (37.2+2) = 39.2
(3(18.6)-5) = (55.8-5) = 50.8
the smaller of the two is the 39.2 degree angle
check your work and see that the two angles add up to 90 :)