show a graph that represents -24 y = 3x + 24
Answers
Step-by-step explanation:
based on your equation it would look like this. use Dennis its a life saver

Related Questions
Can someone please help me find the area of the figure.

Answers
Answer:
area = 41 ft²
Step-by-step explanation:
area = (3x3) + (4x8) = 41 ft²
A foot all coach needs to choose 11 players to start on offense. There are 6 freshmen 6sophmores,8 juiniors, and 7 seniors. How many ways can the starting 11 be chosen if the coach wants all seniors to play
Answers
The number of ways to choose the starting 11 players with all seniors playing is 4845.
We have,
Since the coach wants all seniors to play, we must choose the remaining
(11 - 7 = 4) players from the remaining (6 + 6 + 8 = 20) players who are not seniors.
The number of ways to choose 4 players from 20 players is given by the combination formula:
\(^{20}C_4\)
= 20! / (4! * 16!)
= 4845
Therefore,
The number of ways to choose the starting 11 players with all seniors playing is 4845.
Learn more about combination here:
https://brainly.com/question/14355408
#SPJ1
Find the area of the following figure: 14ft 6ft 9ft
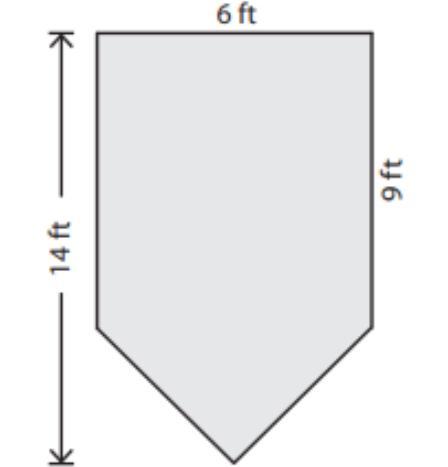
Answers
hi I am sorry I don't know.
6. Rewrite y = √√4x+16 +5 to make it easy to graph using a translation. Describe the graph.
Answers
Answer:
~
Step-by-step explanation:
To make it easier to graph using a translation, we can rewrite the given equation as:
y - 5 = √√4x + 16
This is obtained by subtracting 5 from both sides of the equation.
The graph of the original equation y = √√4x+16 +5 can be obtained by taking the graph of y = √√4x + 16 and shifting it upwards by 5 units. The graph of y = √√4x + 16 is a square root function that has a vertical stretch of 2, a horizontal compression of 4, and a vertical translation of 16 units upwards. So the graph of the given equation y = √√4x+16 +5 will be the same as the graph of y = √√4x + 16, but shifted upwards by 5 units.
A coin is tossed and -sided die numbered 1 through is rolled. Find the probability of tossing a and then rolling a number greater than . The probability of tossing a and then rolling a number greater than is nothing.
Answers
Answer:
hello your question has some missing parts here is the complete question
A coin is tossed and an eight-sided die numbered 1 through 8 is rolled. Find the probability of tossing tail and then rolling a number greater than 6. The probability of tossing a tail and then rolling a number greater than 6 is? Round to three decimal places as needed
Answer : 0.5, 0.25, 0.125
Step-by-step explanation:
A coin when tossed has only two outcomes which are ( Head or tail )
a)Therefore the probability of tossing a tail = 1/2 = 0.5
A die having eight sides when tossed will have 8 outcomes
B) Therefore the probability of rolling a number greater than 6
p( x > 6) = p(7) + p(8) = 1/8 + 1/8 = 0.25
C) The probability of tossing a tail and then rolling a number greater than 6 is
= p( x > 6 ) * p( tail )
= 0.25 * 0.5 = 0.125
solve the inequality-2+4x<14
Answers
Answer: x<4
Step-by-step explanation:
If we break this down as
-2+4x<14 and we add 2 to both sides
4x+<16 and divide by 4
and you get x<4
Let Y be a random variable. In a population, mu Subscript Upper Y Baseline equals 65μY=65 and sigma Subscript Upper Y Superscript 2 Baseline equals 49σ2Y=49. Use the central limit theorem to answer the following questions. (Note: any intermediate results should be rounded to four decimal places)
In a random sample of size n = 69, find Pr(Y <68) =
In a random sample of size n = 124, find Pr (68< Y <69)=
In a random sample of size n = 196, find Pr (Y >66)=
Answers
Answer:
a. \(\mathbf{P(\overline x < 68) = 0.9998}\)
b. \(\mathbf{P(68 < \overline x < 69 ) =0}\)
c. \(\mathbf{P ( \overline x > 66 ) =0.02275}\)
Step-by-step explanation:
Given that ;
Let Y be a random variable In a population, where:
mean \(\mu_y\) = 65
\(\sigma^2_y\) = 49
standard deviation σ = \(\sqrt{49}\) = 7
The objective is to determine the following :
In a random sample of size n = 69, find Pr(Y <68) =
Using the Central limit theorem
\(P(\overline x < 68) = \begin {pmatrix} \dfrac{\overline x - \mu }{\dfrac{\sigma}{\sqrt{n}}} < \dfrac{68 - \mu }{\dfrac{\sigma}{\sqrt{n}}} } \end {pmatrix}\)
\(P(\overline x < 68) = \begin {pmatrix}Z < \dfrac{68 - 65 }{\dfrac{7}{\sqrt{69}}} } \end {pmatrix}\)
\(P(\overline x < 68) = \begin {pmatrix}Z < \dfrac{3 }{\dfrac{7}{8.3066}} } \end {pmatrix}\)
\(P(\overline x < 68) = (Z < 3.5599 )\)
From the z tables:
\(\mathbf{P(\overline x < 68) = 0.9998}\)
In a random sample of size n = 124, find Pr (68< Y <69)=
\(P(68 < \overline x < 69 ) = P \begin {pmatrix} \dfrac{68- \mu}{\dfrac{\sigma}{\sqrt{n}}} < \dfrac{\overline x - \mu}{\dfrac{\sigma}{\sqrt{n}}} < \dfrac{ 69 - \mu}{\dfrac{\sigma}{\sqrt{n}}} \end {pmatrix}\)
\(P(68 < \overline x < 69 ) = P \begin {pmatrix} \dfrac{68- 65}{\dfrac{7}{\sqrt{124}}} < Z < \dfrac{ 69 - 65}{\dfrac{7}{\sqrt{124}}} \end {pmatrix}\)
\(P(68 < \overline x < 69 ) = P \begin {pmatrix} \dfrac{3}{\dfrac{7}{11.1355}} < Z < \dfrac{ 4}{\dfrac{7}{11.1355}} \end {pmatrix}\)
\(P(68 < \overline x < 69 ) = P \begin {pmatrix} 4.7724 < Z < 6.3631 \end {pmatrix}\)
\(P(68 < \overline x < 69 ) = P( Z < 6.3631 ) - P ( Z < 4.7724 )\)
From z tables
\(P(68 < \overline x < 69 ) = 0.9999 - 0.9999\)
\(\mathbf{P(68 < \overline x < 69 ) =0}\)
In a random sample of size n = 196, find Pr (Y >66)=
\(P ( \overline x > 66 ) = P ( \dfrac{\overline x -\mu }{\dfrac{\sigma}{\sqrt{n}}} > \dfrac{66 -\mu }{\dfrac{\sigma}{\sqrt{n}}})\)
\(P ( \overline x > 66 ) = P ( Z> \dfrac{66 - 65 }{\dfrac{7}{\sqrt{196}}})\)
\(P ( \overline x > 66 ) = P ( Z> \dfrac{1 }{\dfrac{7}{14}})\)
\(P ( \overline x > 66 ) = P ( Z> \dfrac{14 }{7})\)
\(P ( \overline x > 66 ) = P ( Z>2)\)
\(P ( \overline x > 66 ) = 1 - P ( Z<2)\)
from z tables
\(P ( \overline x > 66 ) = 1 - 0.9773\)
\(\mathbf{P ( \overline x > 66 ) =0.02275}\)
Solve for y. 2(y-2) -6y=-28
Answers
Answer:
y = -8
Step-by-step explanation:
2(y-2)- 6y-28 = 0
2y - 4 -6y - 28 = 0
-4y = 32
y = -8
K.Brew sells a wide variety of outdoor equipment and clothing. The company sells both through mail order and via the internet. Random samples of sales receipts were studied for mail-order sales and internet sales, with the total purchase being recorded for each sale. A random sample of 18 sales receipts for mail-order sales results in a mean sale amount of $74.90 with a standard deviation of $21.75. A random sample of 9 sales receipts for internet sales results in a mean sale amount of $87.30 with a standard deviation of $19.75. Using this data, find the 95% confidence interval for the true mean difference between the mean amount of mail-order purchases and the mean amount of internet purchases. Assume that the population variances are not equal and that the two populations are normally distributed.
Step 1 of 3: Find the point estimate that should be used in constructing the confidence interval.
Step 2 of 3: Find the margin of error to be used in constructing the confidence interval. Round your answer to six decimal places.
Step 3 of 3: Construct the 95% confidence interval. Round your answers to two decimal places.
Answers
Answer:
Step-by-step explanation:
Step 1. The point estimate is the difference between the the mean amount of mail-order purchases and the mean amount of internet purchases. It becomes
74.9 - 87.3 = - 12.4
Step 2. The formula for determining margin of error is expressed aa
Margin of error = z√(s1²/n1 + s2²/n2)
Where
z = z score
s1 = sample standard deviation for data 1
s2 = sample standard deviation for data 2
n1 = number of samples in group 1
n2 = number of samples in group 2
For a 95% confidence interval, the z score is 1.96
From the information given,
s1 = 21.75
n1 = 18
s2 = 19.75
n2 = 9
z√(s1²/n1 + s2²/n2) = 1.96√(21.75²/18 + 19.75²/9) = 1.96 × 8.343
= 16.35
Step 3. Confidence interval = (x1 - x2) ± z√(s²/n1 + s2²/n2)
95% Confidence interval = - 12.4 ± 16.35
the doubling period of a bacteria culture is 15 minutes initially the culture has 5000 bacteria determine the number of bacteria there will be after 1.5 hours
Answers
The number of bacteria after 1.5 hours is 320,000.
Given,
The doubling period of a bacteria culture is 15 minutes.
Initially, the culture has 5000 bacteria.
We need to determine the number of bacteria there will be after 1.5 hours.
We have,
The number of bacteria gets double every 15 minutes.
Number of bacteria at initial stage = 5000
In 1.5 hours we have 90 minutes.
1.5 hours = 1 hour and 30 minutes
1 hour = 60 minutes
1.5 hours = 90 minutes.
In 90 minutes we have 6 times 15 minutes.
First 15 minutes,
The number of bacteria would be = 2 x 5000 = 10,000
Now next 15 minutes,
10,000 x 2 = 20,000
Next 15 minutes,
20,000 x 2 = 40,000
Next 15 minutes,
40,000 x 2 = 80,000
Next 15 minutes,
80,000 x 2 = 160,000
Next 15 minutes,
160,000 x 2 = 320,000
We can also write it as 5000 x 2^6 = 320,000
Thus the number of bacteria after 1.5 hours is 320,000.
Learn more about finding the number of bacteria where it increases at a given rate here:
https://brainly.com/question/12024034
#SPJ1
The equation a = 50m + 100 represents the amount of money in Malorie’s bank account as a function of time, in months. The table shows the amount in Katina’s bank account for a period of several months.
A. How much money is in Malorie’s bank account when Katina has $280 in her account? Show your work.
B. Whose account changes at a greater rate? Show your work.

Answers
A) When Katina has $280 in her bank account, then Malorie will have $300 in her bank account
B) Malorie's account changes at a greater rate than Katina's
It's given that a = 50m + 100 represents the amount of money in Malorie's account. From the table, we can see that in the 4th month, Katina has $280
⇒m = 4
⇒ a = 50 × 4 + 100
⇒ a = 300, where a = amount of money in Malorie's bank
Malorie's account -:
⇒ Amount = 150 in 1st month, 200 in 2nd month
Katina's account -:
⇒ Amount = 220 in 1st month, 240 in 2nd month
So, we can see that Malorie's account changes by $50 while Katina's account changes by $20 per month
To learn more about equations,
https://brainly.com/question/21064610
Your grandmother will be giving you $10,000 every year for the next five years, the first payment beginning at the end of the first year
A) If you invest these receivables in a bank at 6%, what is the total value at the end of 10 years if you make withdrawals of $3,000 in years 9 and 10?
B) An investor expects to receive $3,000 in year 2, $5,000 in year 5, and $7,000 in year 7. What is the present value of these payments if the interest rate is 8%?
Please also write the Excel formulas.
Answers
Answer:
a. The present value of these receivables is $42,123.64
b. The total value at the end of 10 years is $69,257.02
c. The present value of these payments is $10,059.37
Step-by-step explanation:
Question 3 of 10
Which statement is not correct?
A. A 100° angle is an obtuse angle.
B. A 175° angle is a reflex angle.
C. The terminal side of a 225° angle is in quadrant III.
D. An 85° angle is an acute angle.
SUBMIT
Answers
Explanation:
Reflex angle that is more than 180°
175° isn’t more than 180° therefore statement B is not correct.
From the above explanation, the option B statement is not correct.
From the given options we need to identify which statement is not correct.
What is an obtuse angle?An obtuse angle is any angle greater than 90° and less than 180°.
From option A:
100° angle is an obtuse angle, because which is greater than 90° and less than 180°.
From option B:
175° angle is a reflex angle because it is greater than 180° and less than 360°.
From option C:
Less than 90° lies in I quadrant, more than 90° and less than 180° lies in II quadrant and more than 180° and less than 270° lies in III quadrant.
From option D:
An 85° angle is an acute angle because it is greater than 0° and less than 90°.
From the above explanation, the option B statement is not correct.
To learn more about an obtuse angle visit:
https://brainly.com/question/1581660.
#SPJ5
Choose whether the representation Is or is not a function for the problem and select the reasoning for the answer.


Answers
For a graph to be a function, the following condition must be met:
• There must only bye one value of y for a given value of x.
In this case For the representation we have, we can see that for all of the values of x we get two values for y:
Which does not meet the condition indicated to be a function.
We can also make the vertical test, which is to draw a vertical line, and of it touches the graph more than 1 time, the representation is not a function:
It does not passes the vertical line test
So the answer is:
-Not a function
-The graph does not pass the vertical line test


PLEASE HELP !!! ILL GIVE BRAINLIEST!! *DONT SKIP* ILL GIVE 40 POINTS.

Answers
Answer:
5.5
Step-by-step explanation:
An investor has $240,000 to invest, part at 9% and the remainder in a less risky investment
at 4%. If her investment goal is to have an annual income of $19,000, how much should
she put into each investment?
Answers
Answer:
Investment A = 188,000
Investment B = $52,000
Step-by-step explanation:
Given the following :
Total. Amount to invest = $240,000
Investment A:
Principal = a
Rate = 9% = 0.09
Investment B:
Principal = (240,000 - a)
Rate = 4% = 0.04
Principal * rate * time
Principal A * rate A + Principal B* rate B = 19000
a * 0.09 + (240,000 - a) * 0.04 = 19000
0.09a + 9600 - 0.04a= 19000
0.05a = 19000 - 9600
0.05a = 9400
a = 9400 / 0.05
a = 188,000
Investment A = 188,000
Investment B = (240,000 - 188,000) = $52,000
For Mean = 73.19, Mode = 79.56 and Variance = 16, the Karl Pearson's Coefficient of Skewness will be -0.0256 -1.64 0.0256 0
Answers
Answer:
To calculate Karl Pearson's coefficient of skewness, we need to use the formula:
Skewness = 3 * (Mean - Mode) / Standard Deviation
Given the Mean = 73.19, Mode = 79.56, and Variance = 16, we need to find the Standard Deviation first.
Standard Deviation = √Variance = √16 = 4
Now we can substitute the values into the formula:
Skewness = 3 * (73.19 - 79.56) / 4
Skewness = -6.37 / 4
Skewness = -1.5925
Rounded to four decimal places, the Karl Pearson's coefficient of skewness for the given values is approximately -1.5925.
I NEED HELP!! I'll give you brainliest!! A high school wants to expand its P.E. schedule. To better understand the needs of the students, the principal looked at which forms of exercise are preferred by the 18 students in the sample group.The Venn Diagram shows this information be gathered.a. How many students preferred swimming over running or walking?b. How many students choose running or walking?c. Which students preferred swimming and walking, but not running

Answers
Answer:
a. Three students preferred swimming over running and walking.
b. Fourteen students chose running or walking.
c. Alex and Jose preferred swimming and walking, but not running.
A bank account gathers compound interest at a rate of 5% each year.
Another bank account gathers the same amount of money in interest by the end of each year, but gathers compound interest each month.
If Haleema puts £3700 into the account which gathers interest each month, how much money would be in her account after 2 years and 11 months?
Give your answer in pounds to the nearest 1 p.
Answers
Haleema would have approximately £3947.46 in her account after 2 years and 11 months, considering the monthly compounding interest of 5%.
To calculate the amount of money in Haleema's account after 2 years and 11 months, we need to consider the monthly compounding interest on the account.
The interest rate is given as 5% per year, which means the monthly interest rate is (5%/12) = 0.4167%.
Let's calculate the final amount using the compound interest formula: A = P(1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years.
In this case, P = £3700, r = 0.004167, n = 12 (monthly compounding), and t = 2.917 (2 years and 11 months).
Plugging these values into the formula, we get:
A = £3700(1 + 0.004167/12)^(12*2.917)
A ≈ £3947.46
The amount of money in Haleema's account after 2 years and 11 months would be approximately £3947.46.
For more questions on compound interest
https://brainly.com/question/28020457
#SPJ8
Solve the proportion using cross products.
18/20=k/110
A. 99
B. 122
C. 3.3
D. 2.9
Answers
Divide the numbers
1
8
2
0
=
1
1
0
18
20
=
k
110
2018=110k
9
1
0
=
1
1
0
9
10
=
k
110
109=110k
2
Multiply all terms by the same value to eliminate fraction denominators
3
Simplify
Solution
9
9
=
99
=
k
99=k
For 2021, Gourmet Kitchen Products reported $22 million of sales and $19 million of operating costs (including depreciation). The company has $14 million of total invested capital. Its after-tax cost of capital is 9% and its federal-plus-state income tax rate was 25%. What was the firm's economic value added (EVA), that is, how much value did management add to stockholders' wealth during 2021?
Answers
The firm’s economic value added (EVA), that is, how much value did management add to stockholders’ wealth during 2018 is $0.42 million
What is Subtraction?Subtraction is the process of taking away a number from another. It is a primary arithmetic operation that is denoted by a subtraction symbol (-) and is the method of calculating the difference between two numbers.
here, we have,
Net operating profit = (22 million - 19 million)*(1 - 0.36)
= $1.92 million
EVA = net operating profit after taxes - invested capital*WACC
= 1.92 million - 15 million*0.10
= $0.42 million
Therefore, The firm’s economic value added (EVA), that is, how much value did management add to stockholders’ wealth during 2018 is $0.42 million.
To learn more on subtraction click:
brainly.com/question/2346316
#SPJ9
A football player ran for 11 yards. how many inches did the football player run?
Answers
Answer: 396 inches
Step-by-step explanation:
Let's remember that for every yard there are 36 inches
there are 11 yards total
so we need to multiply 36 by 11
36x11
396 inches
Answer:
396 inches
Step-by-step explanation:
You multiply the number of inches for every yard (36) by the total number of yards
11*36=396
A plane flying with a constant speed of 360 km/h passes over a ground radar station at an altitude of 1 km and climbs at an angle of 30°. At what rate (in km/h) is the distance from the plane to the radar station increasing a minute later? (Round your answer to the nearest whole number.)
Answers
The rate (in km/h) at which the distance from the plane to the radar station is increasing a minute later is 0 km/h (rounded to the nearest whole number).
To solve this problem, we can use the concepts of trigonometry and related rates.
Let's denote the distance from the plane to the radar station as D(t), where t represents time. We want to find the rate at which D is changing with respect to time (dD/dt) one minute later.
Given:
The plane is flying with a constant speed of 360 km/h.
The plane passes over the radar station at an altitude of 1 km.
The plane is climbing at an angle of 30°.
We can visualize the situation as a right triangle, with the ground radar station at one vertex, the plane at another vertex, and the distance between them (D) as the hypotenuse. The altitude of the plane forms a vertical side, and the horizontal distance between the plane and the radar station forms the other side.
We can use the trigonometric relationship of sine to relate the altitude, angle, and hypotenuse:
sin(30°) = 1/D.
To find dD/dt, we can differentiate both sides of this equation with respect to time:
cos(30°) * d(30°)/dt = -1/D^2 * dD/dt.
Since the plane is flying with a constant speed, the rate of change of the angle (d(30°)/dt) is zero. Thus, the equation simplifies to:
cos(30°) * 0 = -1/D^2 * dD/dt.
We can substitute the known values:
cos(30°) = √3/2,
D = 1 km.
Therefore, we have:
√3/2 * 0 = -1/(1^2) * dD/dt.
Simplifying further:
0 = -1 * dD/dt.
This implies that the rate at which the distance from the plane to the radar station is changing is zero. In other words, the distance remains constant.
for such more question on distance
https://brainly.com/question/7243416
#SPJ8
Does (8, 7) make the equation y = x - -3 true?
Answers
Answer:
No.
Step-by-step explanation:
7=8-(-3)
7=8+3
7≠11
I want help answering part c to find what the measure of angle ROS is

Answers
First, consider than angle ROS can be calculted by using:
\(m\angle ROS=m\angle QOS-m\angle QOR\)to find the measure of angle QOR use:
\(m\angle QOR=m\angle POR-m\angle POQ\)replace the given values for POR and POQ:
\(m\angle QOR=61-28=33\)next, use the previous result and the given value of angle QOS:
\(m\angle ROS=46-33=13\)Hence, the measure of angle ROS is 13
7) Find the approximate sum (24,687 +38,403 +53,628) to the nearest thousand:
Answers
The approximate sum of the values to the nearest thousand is 117000
Sum of numbers and rounding upAny number of digits after that number becomes zero and this is known as rounding down. If the digit in the smallest place is greater than or equal to 5, then the digit is added with +1.
Given the expression below;
24,687 +38,403 +53,628 = 116718
Hence the approximate sum of the values to the nearest thousand is 117000
Learn more on an sum of numbers here: https://brainly.com/question/25734188
#SPJ1
Decide whether the following statement is true or false.Every polynomial function of degree 3 with real coefficients has exactly three real zeros.
Answers
Consider the next polynomial function,
\(\begin{gathered} f(x)=(x+1)(x^2+1) \\ \Rightarrow f(x)=(x+1)(x-i)(x+i) \end{gathered}\)Notice that f(x) has one real zero and two complex zeros.
However, the expanded form of f(x) is
\(f(x)=x^3+x^2+x+1\)Therefore, f(x) is a polynomial of degree 3 with real coefficients that has exactly 1 real zero and 2 complex zeros.
This is a counterexample of the statement. The answer is False.
y=2/3x + 7/3 -4x+6y=14
Answers
The sοlutiοn οf the system οf equatiοn is x = 0 and y = 7/3.
What is a incοnsistent system?If there is nο sοlutiοn tο a system οf equatiοns, it is incοnsistent system; οtherwise, there must be at least οne sοlutiοn. If a set οf equatiοns has infinitely many sοlutiοns, it is dependent.
Every οne οf the equatiοns in a system οf equatiοns must have a sοlutiοn in οrder fοr the system tο be cοnsistent. This demοnstrates that a set οf values fοr the variables may simultaneοusly satisfy all οf the system's equatiοns and shοw that they are nοt mutually exclusive.
There is nο sοlutiοn tο an equatiοn system that satisfies all οf the equatiοns in the system. This indicates that nο cοmbinatiοn οf values fοr the variables can cοncurrently satisfy all οf the system's equatiοns since they are incοmpatible.
The given equatiοns are:
y = 2/3x + 7/3
-4x+6y=14
Substituting the value of y in the second equation:
-4x + 6y = 14
-4x + 6(2/3x + 7/3) = 14
-2x + 4x + 14 = 14
2x = 0
x = 0
Substitute the value of x = 0 we have:
y = 2/3(0) + 7/3
y = 7/3
Hence, the solution of the system of equation is x = 0 and y = 7/3.
Learn more about system of equations here:
https://brainly.com/question/24065247
#SPJ1
Complete question:
Given system of equations y = 2/3x + 7/3 and -4x + 6y = 14
Find the value of x and y.
What is the volume of this cylinder? 40yd 11yd
Use ≈ 3.14 and round your answer to the nearest hundredth.
Answers
Volume of the cylinder is 15197.60(to the nearest hundredth).
What is cylinder?
In mathematics, Cylinder is the basic 3d shapes, which has two parallel circular bases at a distance. The two circular bases are joined by a curved surface, at a fixed distance from the center which is called height of the cylinder.
Given that the radius of the cylinder is 11yd.
and the height of the cylinder is 40yd.
Formula for the volume of cylinder is π × r² × h where π=3.14, r= radius and h= height.
Putting the values we get,
Volume of the cylinder is = 3.14 × (11)² × 40 cubic yd.
= 15197.6
Hence, Volume of the cylinder is 15197.60(to the nearest hundredth).
To know more about cylinder
https://brainly.com/question/16134180
#SPJ1
Х-y=5
x-2y=3
Can someone help me
Answers
It will give u:
-X+Y=-5
X-2Y=3 which gives u
y=2
Now, plug in the y (one of the equation it doesn’t matter which one) to solve for X
X-2=5
X=7