simple question: what is 2+2
Answers
Answer:
4
Step-by-step explanation:
Related Questions
How much is 1 oz in mL?
Answers
Answer: 29.5735 is 1 ounces in ml
There is 0.0338 ounces in 1 ml (Using Units).
What are units?
Units are the tools to measure and compare different things. Comparison becomes easy when all the units for the measurement are the same. Different units can be classified depending on their use.
There are two type of units
1. Fundamental Units: Fundamental units are all those units that do not depend on any other unit (including themselves). These units cannot be further reduced to the elementary level. In fact, these are elementary units. Only seven fundamental units exist in Metric System or SI system which are
Length (meter, m)
Mass (kilogram, kg)
Time (second, s)
Temperature (kelvin, K)
Amount of substance (mole, mole)
Electric current (ampere, A)
Luminous intensity (candela, cd)
2. Derived units:These units are all those units that are obtained by multiplying and/or dividing one or more fundamental units with or without introducing any other numerical factor. These units can be reduced to their elementary level, which is composed of fundamental units. There exist a large number of derived units in the Metric System.
Examples:
Velocity (m/s)
Acceleration (m/s2)
Momentum (kg-m/s)
Force (N)
Density (kg/m3)
Heat (J)
Energy (J)
Power (W), etc.
Now, To change 1ml to ounces
divide 1ml by 29.574 this will give us value in ounces
Therefore, 1ml/29.574= 0.0338 ounces
hence,
There is 0.0338 ounces in 1 ml.
To know more about units visit the link
https://brainly.com/question/10433377?referrer=searchResults
#SPJ4
Find the average value of the function f(x) = (x + 2) on the interval [0, 3].
![Find the average value of the function f(x) = (x + 2) on the interval [0, 3].](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/P5zl0SIYRlJ5Lz5JinzKHjLeHoS5AWmn.png)
Answers
The average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Calculate the definite integral of the function over the interval [a, b], then divide it by the interval's length (b - a), in order to determine the average value of a function f(x) over the interval.
Given that the interval is [0, 3] and the function f(x) = (x + 2), we have:
= (1/3) × [1/2 x² + 2x] evaluated from x=0 to x=3
= (1/3) × [(1/2 × 3² + 2×3) - (1/20² + 20)]
= (1/3) × [(9/2 + 6) - 0]
= (1/3) × (21/2)
= 7/2
Therefore, the average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Learn more about definite integral click;
https://brainly.com/question/30760284
#SPJ1
i need help on how to find m and b
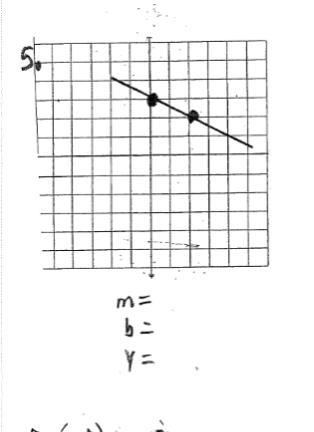
Answers
Answer:
y = \(-\frac{1}{2}x+3\)
Step-by-step explanation:
Slope of line passing through two points \((x_1,y_1)\) and \((x_2,y_2)\) is give by,
Slope 'm' = \(\frac{y_2-y_1}{x_2-x_1}\)
Therefore, slope of the line passing through the points (0, 3) and (2, 2),
m = \(\frac{3-2}{0-2}\) = \(-\frac{1}{2}\)
Y-intercept 'b' of the given line in the graph is (3).
Since, equation of line with slope 'm' and y-intercept 'b' is,
y = mx + b
Therefore,equation of the line given in graph will be,
y = \(-\frac{1}{2}x+3\)
why is this true 7a+4-2a=7a+ -2a+4
Answers
Answer:
Step-by-step explanation:
Notice that both sides involve 7a - 2a, and both involve 4. By the associative property the order in which the addends appear is immaterial; the left side therefore equals the right side.
Answer:
7a + 4 - 2a = 7a - 2a + 4
5a + 4 = 5a + 4
Step-by-step explanation:
7a + 4 - 2a = 7a - 2a + 4
7a + 4 - 2a
Rearrange the terms.
7a - 2a + 4
Combine like terms.
5a + 4
The left side simplifies to 5a + 4.
7a - 2a + 4
5a + 4
The right side also simplifies to 5a + 4.
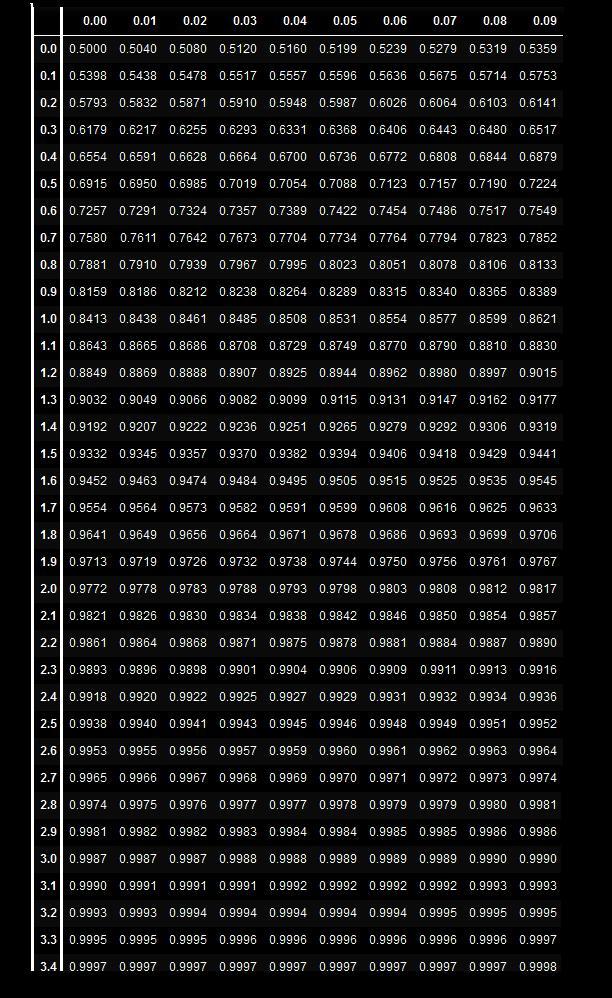
suppose that the distribution of the number of steps he takes is normally distributed with a mean of 10,000 and a standard deviation of 1,500 steps. how many steps would he have to take to make the cut for the top 5% for his distribution?
Answers
The number of steps he would have to take to make the cut for the top 5% for his distribution is 12,031.5.
The number of steps he would have to take to make the cut for the top 5% for his distribution is 12,031.5.
Suppose that the distribution of the number of steps he takes is normally distributed with a mean of 10,000 and a standard deviation of 1,500 steps. So, the population parameters are:
Mean=μ=10,000
Standard Deviation=σ=1,500
We need to find the number of steps he would have to take to make the cut for the top 5% for his distribution.
Step 1: We need to find out the z-score for the top 5% of the distribution.
We can find out the z-score for the top 5% of the distribution using the standard normal distribution table. The table value of z for 0.05=1.645. Check the attachment.
Step 2: We can use the z-score formula to find out the value of X for the top 5% of the distribution.
z=(X-μ)/σ
Rearranging the above equation, we get:
X=μ+z.σ
X=10,000+1.645×1,500
X=12,031.5
Therefore, It would take him 12,031.5 steps to make the top 5% for his distribution.
To know more about distribution: https://brainly.com/question/26678388
#SPJ11
Question 10 of 28
Which of the following expressions are equivalent to
2. ? Choose all that apply.
ھر - 20
A.
B.
c.
2
(3)2 - (13 )2
1
1
(x3 - 3 ) ( + 13 )
2
1
(3 - 13) (3 - 13)
مردم زمرے
2
1
D. (x3 - 3 ) ( + 13 )

Answers
Answer: A, D
Step-by-step explanation:
A) Correct. \((x^3)^2=x^{(3)(2)}=x^6\). Similar logic for y.
B) Incorrect. The numerators are different.
C. Incorrect. The denominators are not the same.
D. Correct. The denominators are the same by difference of squares.
NEED HELP ASAP
PLEASE HELP, WILL GIVE BRAINLIEST

Answers
Answer:
8 1/8
Step-by-step explanation:
1st I'm going to turn these into improper fractions with a golf swing (multiply the bottom, add the top, keep denominator the same)
3 times 4 + 3 = 15, so we get 15 over 4
4 times 8 + 3 = 35, so we get 35 over 8
Next I am going to give them a common denominator. (Their least common multiple is 8)
one denominator is already 8, so we need to fix the other one by multiplying it by two (multiply both sides)
15/4 times 2/2 = 30/8
Now we add the two fractions (DO NOT ADD DENOMINATORS)
30/8 + 35/8 = 65/8
Finally to make it a mixed number, ask self, how many times does 8 go into 65? 8 times. That's the whole number. what's left over? 1. That is the numerator. The denominator stays the same.
QUESTION 5 [10] 5.1. Mr Nkosi is planning a trip to go to Johannesburg for holidays. A car hiring company offers Mr Nkosi a rental car for R240.00 per day. They also charge 1.20 per KM. Mr Nkos (4) hired the car for 7 days and travelled 1140km. how much is he going to pay? Page 4 of 5
Answers
The total cost that Mr. Nkosi must pay is equal to 3048 rands.
How much money should Mr. Nkosi pay for renting a car?
The statement indicates that total cost (T), in monetary costs, for renting a car is the result of adding a fixed cost (F(t)), in monetary units, related to the time (t), in days, and a variable cost (V(s)), in monetary units, related to the travelled distance (s), in kilometers.
The total cost that Mr. Nkosi must pay is described by the following linear equation:
T = F(t) + V(s)
The following conditions are given:
F(t) = 240 · t
V(s) = 1.20 · s
Thus,
T = 240 · t + 1.20 · s
If we know that t = 7 and s = 1140 km, then the total cost is:
T = 240 · 7 + 1.20 · 1140
T = 3048
Mr. Nkosi must pay a total cost of 3048 rands.
To learn more on total costs: https://brainly.com/question/14592299
#SPJ1
What is the answer to x? Given the top of the triangle is 80.

Answers
El administrador de una cafetería sabe que vende diariamente 50 litros de jugo mixto. Para elaborar este jugo se emplean dos preparados: uno de jugo de naranja, que contiene un 5% de jugo natural y otro preparado de jugo de toronja, que contiene 25% de jugo natural. Si se desea que el jugo mixto contenga un 10% de jugo natural, ¿Cuántos litros de cada preparado se deben emplear?
Answers
Answer:
El administrador debe usar 37.5 litros de jugo al 5% y 12.5 litros de jugo al 25%.
Step-by-step explanation:
Sistemas de Ecuaciones
Llamamos:
x = litros de jugo al 5% natural
y = litros de jugo al 25% natural
El administrador de la cafetería desea hacer 50 litros de jugo, luego:
x + y = 50 [1]
Esos 50 litros de jugo deben tener 10% de jugo natural. Como cada parte de x aporta 5% y cada parte de y aporta 25%:
5x + 25y = 10*50 = 500
Dividimos entre 5:
x + 5y = 100 [2]
Restamos [2] menos [1]:
4y = 50
y = 50/4 = 12.5
De [1] tenemos que:
x = 50 - y = 50 - 12.5 = 37.5
El administrador debe usar 37.5 litros de jugo al 5% y 12.5 litros de jugo al 25%.
A quadratic expression is shown. x^2-6x+7 Rewrite the expression by completing the square.
Answers
Answer:
X= 1 or X = -7
Step-by-step explanation:

What evidence is needed to prove two triangles are similar by the SSS similarity theorem?
Answers
Consider the same figure as given above. It is observed that DP/PE = DQ/QF and also in the triangle DEF, the line PQ is parallel to the line EF.
So, ∠P = ∠E and ∠Q = ∠F.
Hence, we can write: DP/DE = DQ/DF= PQ/EF.
The above expression is written as
DP/DE = DQ/DF=BC/EF.
It means that PQ = BC.
Hence, the triangle ABC is congruent to the triangle DPQ.
(i.e) ∆ ABC ≅ ∆ DPQ.
Thus, by using the AAA criterion for similarity of the triangle, we can say that
∠A = ∠D, ∠B = ∠E and ∠C = ∠F.
To know more about triangle check the below link:
https://brainly.com/question/1058720
#SPJ4
The function (x) = 0.42x + 50 represents the cost (in dollars) of a one-day truck rental when the truck is
driven x miles.
a. What is the truck rental cost when you drive 85 miles?
b. How many miles did you drive when your cost is $65.96?
Answers
a. The truck rental cost when you drive 85 miles is $85.7.
b. The number of miles driven when the cost is $65.96 is 0.42x.
a. To find the truck rental cost when driving 85 miles, we can substitute the value of x into the given function.
f(x) = 0.42x + 50
Substituting x = 85:
f(85) = 0.42(85) + 50
= 35.7 + 50
= 85.7
Therefore, the truck rental cost when driving 85 miles is $85.70.
b. To determine the number of miles driven when the cost is $65.96, we can set up an equation using the given function.
f(x) = 0.42x + 50
Substituting f(x) = 65.96:
65.96 = 0.42x + 50
Subtracting 50 from both sides:
65.96 - 50 = 0.42x
15.96 = 0.42x
To isolate x, we divide both sides by 0.42:
15.96 / 0.42 = x
38 = x
Therefore, the number of miles driven when the cost is $65.96 is 38 miles.
In summary, when driving 85 miles, the truck rental cost is $85.70, and when the cost is $65.96, the number of miles driven is 38 miles.
For similar question on equation.
https://brainly.com/question/25976025
#SPJ8
For a fund-raiser, a boy scout troop sold two sizes of popcorn boxes-small, s for $3 and large,g, for $6. If 302 boxes were sold with cash receipt of $1,803, how many large boxes were sold?
Answers
To determine the number of large popcorn boxes sold by a boy scout troop, given that they sold a total of 302 boxes with a cash receipt of $1,803, we can set up a system of equations.
Let's assign variables to the number of small boxes (s) and large boxes (g) sold. We know that the price of a small box is $3 and the price of a large box is $6. We also know that the total number of boxes sold is 302 and the cash receipt is $1,803.
We can set up the following system of equations:
s + g = 302 (equation 1)
3s + 6g = 1,803 (equation 2)
From equation 1, we can deduce that s = 302 - g.
Substituting this value of s into equation 2, we get:
3(302 - g) + 6g = 1,803
Expanding and simplifying:
906 - 3g + 6g = 1,803
Combining like terms:
3g = 897
Dividing both sides by 3:
g = 299
Therefore, the number of large boxes sold is 299.
Learn more about equations .here:
https://brainly.com/question/29538993
#SPJ11
Batch Testing: Determine the probability of a negative result for a batch of size 10 if the positivity rate is 10%. Type your numeric answer and submit
Answers
The probability of a negative result for a batch of size 10 is approximately 0.3487 or 34.87%.
To determine the probability of a negative result for a batch of size 10, we need to calculate the probability that all 10 samples in the batch are negative.
Given that the positivity rate is 10%, it means that the probability of a sample being positive is 0.10, and the probability of a sample being negative is 0.90.
To find the probability of all 10 samples being negative, we multiply the probabilities of each sample being negative together:
Probability of a negative result for a single sample = 0.90
Probability of all 10 samples being negative = (0.90)^10 ≈ 0.3487
Therefore, the probability of a negative result for a batch of size 10 is approximately 0.3487 or 34.87%.
To learn more about PROBABILITY click here:
brainly.com/question/24708110
#SPJ11
Please ' help me I need it please I'm begging you

Answers
Answer: 0.75 (choice B)
=============================================
Explanation:
One way to set up the equation is to think of it like this
vertical/horizontal = vertical/horizontal
So we could say
(3.5)/(28) = x/6
Cross multiply and solve for x
3.5*6 = 28*x
21 = 28x
x = 21/28
x = (3*7)/(4*7)
x = 3/4 in fraction form
x = 0.75 in decimal form
-------------
Another possible set up equation is
28/6 = (3.5)/x
in this case I divided the horizontal sides together (28 and 6) and the vertical sides divide to form their own separate fraction as well.
Solving that equation should lead you to x = 3/4 = 0.75
Other equations are possible.
What is the quotient of y/4 divided y/8
Answers
Answer:
2
Step-by-step explanation:
when you divide fraction, you flip the second fraction and change to multiply
y/4 *8/y =8/4 =2
Answer:
2
Step-by-step explanation:
\(\frac{y}{4}\)÷\(\frac{y}{8}\)
= \(\frac{y}{4}\) × \(\frac{8}{y}\)
= \(\frac{8y}{4y}\)
= 2
Hope this helps <_>
please help!!
-2x + 2y=-4 x-4y=-10 solve by elimination
Answers
Step-by-step explanation:
To solve by elimination, we need to get the coefficients of either x or y the same for both equations.
Let's first multiply the second equation by 2, so that the coefficients of x become opposite in sign:
-2x + 2y = -4
2x - 8y = -20
Now, we can add the two equations together to eliminate x:
(2x - 8y = -20)
(-2x + 2y = -4)
-6y = -24
Dividing both sides by -6, we get:
y = 4
Now, we can substitute this value of y into either of the original equations to solve for x. Let's use the first equation:
-2x + 2y = -4
-2x + 2(4) = -4
-2x + 8 = -4
-2x = -12
x = 6
Therefore, the solution is (x, y) = (6, 4).
Answer:
To solve this system of equations by elimination, we need to eliminate one of the variables, either x or y. Let's choose to eliminate y:
-2x + 2y = -4
x - 4y = -10
Multiplying the second equation by 2, we get:
-2x + 2y = -4
2x - 8y = -20
Now we can add the two equations to eliminate y:
-2x + 2y + 2x - 8y = -4 - 20
Simplifying, we get:
-6y = -24
Dividing both sides by -6, we get:
y = 4
Now we can substitute y = 4 into one of the equations to solve for x. Let's use the first equation:
-2x + 2y = -4
-2x + 2(4) = -4
Simplifying, we get:
-2x + 8 = -4
Subtracting 8 from both sides, we get:
-2x = -12
Dividing both sides by -2, we get:
x = 6
Therefore, the solution to the system of equations is (x, y) = (6, 4).
please help 6th grade math

Answers
Answer:
B
Step-by-step explanation:
A population has a mean of 180 and a standard deviation of 36. A sample of 84 observations will be taken. The probability that the sample mean will be between 181 and 185 is.
Answers
A population has a mean of 180 and a standard deviation of 36. A sample of 84 observations will be taken. The probability that the sample mean will be between 181 and 185 is
Given n(sample size) = 84
Population mean(μ) = 180
Standard Deviation(σ) = 36
Standard error of the mean = σx-bar = σ/√n = 36/√84 = 36/9.165 = 3.927
Standardizing the sample mean we have
Z = (x-bar - μ)/σx-bar = (x-bar - μ)/σ/√n
x-bar = 180
Z(x-bar=185 at point C) = (185 - 180)/3.927 = 5/3.927 = 1.273
Z(x-bar=181 at point D) = (181 - 180)/3.927 = 1/3.927 = 0.254
The area ABCD is the probability that the sample mean will lie between 181 and 185.
The shaded Area ABCD = (Area corresponding to Z = 2 or x-bar = 185) - (Area corresponding to Z = 1 or x-bar = 181)
Area corresponding to Z = 1.273 = 0.898
Area corresponding to Z = 0.254 = 0.598
The shaded Area ABCD = 0.898-0.598 = 0.300
Therefore the probability that the sample mean will lie between 181 and 185 is 0.300.
To learn more about Probability, click here https://brainly.com/question/25870256
#SPJ4
PLEASE HELP! WILL MARK BRAINLIEST - What is 2(n+1)?
Answers
Answer:
2n + 2
Step-by-step explanation:
To get the answer you must do distributive. This means you have to multiply 2 and N and 2 and 1. Next, after you multiply these answers you put them together with whatever operation sign is there. In this case, the operation sign here is an addition. Therefore the answer would be 2n + 2.
you want to have 90% confidence of estimating the proportion of office workers who respond to e-mail within - 0.05 an hour to within because you have not previously undertaken such a study, there is no information available from past data. determine the sample size needed.
Answers
Answer:Can you explain this better
Step-by-step explanation:
Answer:
A sample of 675 office workers would be needed to estimate the proportion of workers who respond to emails within 0.05 hours with 90% confidence.
Step-by-step explanation:
To determine the sample size needed, we need to use the following formula:
n = (Z^2 * p * q) / E^2
Where:
n is the sample size needed
Z is the Z-score corresponding to the desired level of confidence (in this case, 90% confidence corresponds to a Z-score of 1.645)
p is the estimated proportion of office workers who respond to e-mail within the desired time frame (we don't have an estimate, so we will assume a conservative estimate of 0.5)
q is the complement of p (q = 1 - p)
E is the margin of error we want to achieve (in this case, 0.05)
Plugging in the values, we get:
n = (1.645^2 * 0.5 * 0.5) / 0.05^2
n = 674.52
Rounding up to the nearest whole number, we get a sample size of 675. Therefore, we would need to sample 675 office workers in order to estimate the proportion of workers who respond to e-mails within 0.05 hours with 90% confidence.
need help ASAPPPPP , what is the volume of the sphere?

Answers
Answer:
\(V =33.5\ inches\)
Step-by-step explanation:
Step 1: Find the volume of the sphere
Formula for the volume of a sphere: \(V=\frac{4}{3}\pi r^{3}\)
\(Radius = Diameter / 2\)
\(Radius = 4 / 2\)
\(Radius = 2\)
\(V=\frac{4}{3}(3.14) (2)^{3}\)
\(V =33.5\ inches\)
Answer: \(V =33.5\ inches\)
The area for any square is given by the function f(x)=x2, where x is the length of a side of the square. Find and interpret f(3.5).
f(3.5)= ______ which means the area of a square with a side of length _______ units is _____ square units
Answers
Answer:
see explanation
Step-by-step explanation:
f(x) = x² , then
f(3.5) = 3.5² = 12.25
which means the area of a square with a side of length 3.5 units is 12.25 units²
The area of a square with a side of length 3.5 units is 12.25 square units.
What is an area?Area is the quantity that expresses the extent of a region on the plane or on a curved surface.
Given that, the area for any square is given by the function f(x) = x², where x is the length of a side of the square
f(x) = x²
f(3.5) = 3.5²
f(3.5) = 12.25
Hence, The area of a square with a side of length 3.5 units is 12.25 square units.
For more references on area, click;
https://brainly.com/question/27683633
#SPJ5
For Gardyloo Manufacturing, the true proportion of accounts receivable with some kind of error is .20. If an auditor randomly samples 225 accounts receivable, what is the approximate normal probability that more than 39 will contain errors?
Answers
Main Answer:The approximate normal probability that more than 39 accounts receivable will contain errors is approximately 84.13%.
Supporting Question and Answer:
What is the significance of using the normal approximation to the binomial distribution in solving the given problem?
The normal approximation to the binomial distribution is employed when certain conditions are met, namely a large sample size (n ≥ 30) and both np and n(1-p) being greater than 5. This approximation allows us to estimate the probabilities associated with the binomial distribution using the standard normal distribution. By utilizing this approximation, we can simplify calculations and apply readily available tools such as z-scores and normal distribution tables or calculators. It enables us to estimate the probability of events, such as obtaining a certain number of accounts with errors, without relying on computationally intensive calculations associated with the binomial distribution formula.
Body of the Solution: To solve this problem, we can use the normal approximation to the binomial distribution. When the sample size is large (n ≥ 30) and both np and n(1-p) are greater than 5, we can approximate the binomial distribution with a normal distribution.
Given: True proportion of accounts receivable with errors (p) = 0.20 Sample size (n) = 225
To calculate the probability that more than 39 accounts receivable will contain errors, we need to find the probability of getting 39 or fewer accounts with errors and then subtract it from 1.
Let's calculate the mean (μ) and standard deviation (σ) of the binomial distribution:
μ = n × p
= 225 × 0.20
= 45
σ = √(n ×p × (1 - p))
= √(225 × 0.20× (1 - 0.20))
= √(225 × 0.20 × 0.80)
=6
Now, let's calculate the z-score for 39:
z = (x - μ) / σ
= (39 - 45) / 6
= -1
Using a standard normal distribution table or calculator, we can find the probability associated with the z-score of -1, which is approximately 0.1587.
The probability of getting 39 or fewer accounts with errors is 0.1587.
To find the probability of more than 39 accounts with errors, subtract the above probability from 1:
P(X > 39) = 1 - P(X ≤ 39)
= 1 - 0.1587
= 0.8413
Therefore, the approximate normal probability that more than 39 accounts receivable will contain errors is approximately 0.8413, or 84.13%.
Final Answer: Thus, the approximate normal probability that more than 39 accounts receivable will contain errors is approximately 84.13%.
To learn more about the significance of using the normal approximation to the binomial distribution from the given link
https://brainly.com/question/9325204
#SPJ4
The approximate normal probability that more than 39 accounts receivable will contain errors is approximately 84.13%.
The normal approximation to the binomial distribution is employed when certain conditions are met, namely a large sample size (n ≥ 30) and both np and n(1-p) being greater than 5. This approximation allows us to estimate the probabilities associated with the binomial distribution using the standard normal distribution. By utilizing this approximation, we can simplify calculations and apply readily available tools such as z-scores and normal distribution tables or calculators. It enables us to estimate the probability of events, such as obtaining a certain number of accounts with errors, without relying on computationally intensive calculations associated with the binomial distribution formula.
To solve this problem, we can use the normal approximation to the binomial distribution. When the sample size is large (n ≥ 30) and both np and n(1-p) are greater than 5, we can approximate the binomial distribution with a normal distribution.
Given: True proportion of accounts receivable with errors (p) = 0.20 Sample size (n) = 225
To calculate the probability that more than 39 accounts receivable will contain errors, we need to find the probability of getting 39 or fewer accounts with errors and then subtract it from 1.
Let's calculate the mean (μ) and standard deviation (σ) of the binomial distribution:
μ = n × p
= 225 × 0.20
= 45
σ = √(n ×p × (1 - p))
= √(225 × 0.20× (1 - 0.20))
= √(225 × 0.20 × 0.80)
=6
Now, let's calculate the z-score for 39:
z = (x - μ) / σ
= (39 - 45) / 6
= -1
Using a standard normal distribution table or calculator, we can find the probability associated with the z-score of -1, which is approximately 0.1587.
The probability of getting 39 or fewer accounts with errors is 0.1587.
To find the probability of more than 39 accounts with errors, subtract the above probability from 1:
P(X > 39) = 1 - P(X ≤ 39)
= 1 - 0.1587
= 0.8413
Therefore, the approximate normal probability that more than 39 accounts receivable will contain errors is approximately 0.8413, or 84.13%.
Thus, the approximate normal probability that more than 39 accounts receivable will contain errors is approximately 84.13%.
To learn more about binomial distribution from the given link
brainly.com/question/9325204
#SPJ4
On Sunday, Sheldon bought 412 kg of plant food. He used 123 kg on his strawberry plants and used 14 kg for his tomato plants. How many kilograms of plant food did Sheldon have left?
Answers
Answer:
...............................
Chi-square distributions that are positively skewed have a research hypothesis that is?
Answers
Answer:
A one tailed test
Step-by-step explanation:
Chi-Square Distributions That Are Positively Skewed Have A Research Hypothesis That Is A One-Tailed Test.
Chi-Square distributions are positively skewed, with the degree of skew decreasing with increasing degrees of freedom.
#SPJ4
learn more on chi square
https://brainly.com/question/14082240
One-Tailed Test
In probability theory and statistics, the chi-square distribution with k degrees of freedom is the distribution of the sum of squares of k independent standard normal random variables. The chi-square distribution is a continuous probability distribution. The shape of the chi-square distribution depends on its degrees of freedom k. It is used to describe the distribution of the sum of squares of random variables. The chi-square distribution is positively skewed, with decreasing skewness as the degrees of freedom increase. The chi-squre distribution approaches the normal distribution on increase of degree of freedom.Chi-Square distributions that are positively skewed have a research hypothesis that is a One-Tailed Test.
Learn more about chi-square distribution
https://brainly.com/question/4543358
#SPJ4
It is assumed that the average Triglycerides levet in a healthy person is 130 unit. In a sample of 30 patients, the sample mean of Triglycerides level is 122 and the sample standard deviation is 20. Calculate the test statistic value
Answers
The test statistic value for this situation is approximately -2.474.
A hypothesis test comparing the sample mean to the assumed population mean is necessary in order to determine the value of the test statistic. The population mean triglycerides level would be the null hypothesis (H0), and the alternative hypothesis (Ha) would be that the population mean is not 130 units.
The t-statistic, which is calculated as follows, is the test statistic utilized in this circumstance:
t = (test mean - expected populace mean)/(test standard deviation/sqrt(sample size))
Given the data gave, we have:
Expected populace mean (μ): 130 Mean of the sample (x): 122
Test standard deviation (s): 20 (n) sample sizes: 30
Connecting the qualities into the recipe, we can work out the test measurement:
t = (122 - 130) / (20 / sqrt(30)) t = -8 / (20 / sqrt(30)) After calculating this expression, we come to the following conclusion:
t ≈ - 2.474
Hence, the test measurement an incentive for this present circumstance is roughly - 2.474.
To know more about standard deviation refer to
https://brainly.com/question/29115611
#SPJ11
A scenario in which the optimal objective function contour line coincides with one of the binding constraint lines on the boundary of the feasible region leads to _____ solutions. Group of answer choices infeasible alternative optimal binding unique optimal
Answers
Answer: Alternative optimal
Step-by-step explanation:
Alternative optimal solution means that
there are several optimal solutions that can be used to get identical objective function value.
Therefore, a scenario whereby the optimal objective function contour line coincides with one of the binding constraint lines on the boundary of the feasible region will lead to alternative optimal solution.
Please help solve im stuck!

Answers
Answer:
Step-by-step explanation:
The statement that is not true (an exception is easily created) is C
Draw a 1 by 4 rectangle.
Underneath it draw a 2 by 2 rectangle.
They both have the same area (4 units) but they are not congruent. The corresponding lengths are not equal and that is another condition that must be met for there to be congruence. There are many others.
Draw a 2 by 2 square.
draw a triangle with a base of 1 and a height of 8. These two figures have the same area, but they don't even have the same number of sides.
C is simply not true.