Solve (2x - 1)^2 = 9.
A. X = 2, -1
B. X = -2,1
C. x = -2, -1
D. X = 2,1
Answers
Answer:
x=2, -1
Step-by-step explanation:

Related Questions
Can someone please help me with this? I'm not sure how to do it.

Answers
The number horizontally, on the bottom of the grid are the x values. The numbers vertically, going up are the y-values.
So,
O has coordinates x = 1 and y= 1 so it will be (1,1)
E has coordinates x=1 and y = 11 so it will be (1,11)
T has coordinates x=2 and y = 5 so it will be (2,5)
So on…
DO THE MATH: Skipper has a credit card account that charges 19% APR using 31
day billing periods. On the first day of the billing period, Skipper buys marine-grade
rope for $933 on the credit card. No other purchases are made. Skipper pays off the
purchase on day 31 at the end of the billing period. What is Skipper's finance
charge? Round your answer to the nearest penny.
Purchase
Day Description
1
Marine-grade rope
Payment
4
Amount
$933.00
Day Amount
31 $933.00
The table below will help you calculate the finance charge.
Answers
Skipper's finance charge at the end of the billing period is given as follows:
$14.77.
How to obtain the finance charge?The finance charge is obtained using simple interest, as there is a simple compounding per year for the debt, and the charge is the amount of interest accrued during the period of one month.
The amount of interest accrued after t years, using simple interest, is given as follows:
I(t) = Prt.
The parameters for the equation are given as follows:
P is the principal.r is the interest rate, as a decimal.t is the time, in years.Considering a period of one month = 1/12 of an year, the values of these parameters for this problem are given as follows:
P = 933, r = 0.19, t = 1/12.
Hence the finance charge for Skipper's purchase is calculated as follows:
I = 933 x 0.19 x 1/12 = $14.77.
(rounding to the nearest penny = nearest cent).
More can be learned about simple interest at https://brainly.com/question/20690803
#SPJ1
2. Graph the following equation: y = - 1/2 x + 4
Answers
Answer:
Step-by-step explanation:
y = (-1/2)x + 4 is the equation of a straight line with y-intercept (0, 4) and slope -1/2.
To graph this, first plot the y-intercept (0, 4).
Recall that slope m = rise / run, and notice that the slope in this particular case is -1/2 = rise / run, or rise = -1 and run = 2.
Starting with your pencil point on (0, 4), move the point 2 units to the right (run = 2), arriving at (2, 4). Next, move your pencil point 1 unit down, to (2, 3).
Draw a straight line through (0, 4) and (2, 3).
Find the surface area of the triangular prism. The base of the prism is an
isosceles triangle.
The surface area is cm Superscript 2.
37 cm
35 cm
47 cm
24 cm

Answers
Answer:
5446cm²
Step-by-step explanation:
the surface area = the 2 isosceles triangles + the 2 sides + the base
= 2 (24/2 X 35) + 2(37 X 47) + (47 X 24)
= 5446cm²
Answer: 5,446 cm²
Step-by-step explanation:
First, we will find the area of the two triangle sides.
A = 2 * (\(\frac{bh}{2}\))
A = bh
A = (35 cm)(24 cm)
A = 840 cm²
Next, we will find the area of the three rectangular sides. We have two that are congruent and a third that is not.
A = 2 * (LW)
A = 2 * ((47 cm)(37 cm))
A = 2 * 1,739 cm²
A = 3,478 cm²
A = LW
A = (24 cm)(47 cm)
A = 1,128 cm²
Lastly, we will add all of these faces together.
840 cm² + 3,478 cm² + 1,128 cm² = 5,446 cm²
Find the critical value zα2/ that corresponds to a 91% confidence level. Question 13 options: a) 1.7 b) 1.95 c) 1.81 d) 2.33 e) 2.57
Answers
Answer:
D
Step-by-step explanation:
2.33 I think
The critical value that corresponds to a 91% confidence level is 1.7
What is critical value?'Critical value is a cut-off value that is used to mark the start of a region where the test statistic, obtained in hypothesis testing, is unlikely to fall in. In hypothesis testing, the critical value is compared with the obtained test statistic to determine whether the null hypothesis has to be rejected or not.'
According to the given problem,
Confidence level = 91%
Now, α = ( 100 - 91 ) %
= 9%
= 0.09
Area of each tail = \(\frac{0.09}{2}\)
= 0.045
Area in the middle = 1 - 0.045
= 0.955
Now, if we look up this area on the z-table, the critical value will come as 1.6954, which is nearly equal to 1.7.
Hence, we can conclude, the critical value is 1.7.
Learn more about critical value here: https://brainly.com/question/14508634
#SPJ2
Alan is building a garden shaped like a rectangle with a semicircle attached to one short side. If he has 90 feet of fencing to go around it, what dimensions will give him the maximum area in the garden.
Answers
Answer:
long side, semicircle diameter: 180/(4+π) ft ≈ 25.2 ftshort side: 90/(4+π) ft ≈ 12.6 ftStep-by-step explanation:
Let the rectangle dimensions be x and y. Assume that x represents the "short" side, so it is also the diameter of the semicircle. Then the perimeter is ...
P = x + 2y + πx/2 = 90
The area is the area of the rectangle added to the area of the semicircle:
A = xy + (1/2)π(x/2)^2 = x(π/8x +y)
Solving the perimeter equation for y, we get
y = (90 -x -π/2x)/2
and the area equation becomes ,..
A = x(π/8x +45 -x/2 -π/4x)
A = x(45 -x(1/2 +π/8))
The graph of A(x) is a parabola opening downward with zeros at x=0 and x=45/(1/2+π/8) = 360/(4+π).
The vertex (maximum) of the area curve will be halfway between the zeros, at ...
x = (0 +360/(4+π))/2 = 180/(4+π)
The value of y is then ...
y = (90 -x(1 +π/2))/2 = (1/2)(90 -(180/(4+π))(2+π)/2) = (1/2)(90)(1 -(2+π)/(4+π))
y = 45(4+π-2-π)/(4+π) = 90/(4+π)
The rectangle dimensions are 90/4+π) by 180/(4+π), with the semicircle diameter equal to 180/(4+π).
__
That's about 25.2 ft by 12.6 ft with the semicircle attached to the long side.
_____
Please note that the overall dimensions of the garden are the same in both directions. It is effectively "square" with two corners rounded into quarter circles.

Genesis is older than Dylan. Their ages are consecutive integers. Find Genesis's age if
the product of their ages is 110.
(ill give brainliest )
Answers
Answer:
Dylan is 10 years old, and Genesis is 11.
Step-by-step explanation:
If Genesis and Dylan's age are consecutive integers, and Genesis is older, we can represent their ages as:
Dylan's age: x
Genesis' age: x+1
This would mean Genesis is a year older than Dylan.
The product of their ages is 110.
We can write an equation:
x×(x+1)=110
x²+x=110 (Distribute x)
x²+x-110=0 (Move 110 to the other side)
You can solve this by the quadratic equation, by factoring or by completing the square
I'll solve it by the quadratic equation:
We must first find the coefficients a, b and c, and then plug it into the formula.
\(x = \frac{ - 1 + - \sqrt{ {1}^{2} - 4 \times 1 \times - 110} }{2 \times 1} \\ x = \frac{ - 1 + - \sqrt{1 + 440} }{2} \\ x = \frac{ - 1 + - 21}{2} \)
Since we have a ± symbol, we get 2 real solutions, x1 and x2.
x=-1±21/2
x1=-1+21/2
x1=20/2
x1=10
x2=-1-21/2
x2=-22/2
x2=-11
Since their age can't be negative, x2 can't be a solution, so Dylan's age must be 10, and Genesis' age must be 11.
Hope this helps, and let me know if you need help with another method to solve this problem!
Find the first three powers, A, A2, and A3, of the transition matrix below. Find the probability that state 1 changes to state 2 after three repetitions of the experiment. 0.3 0.1 0.6 A0.5 0.2 0.3 Type an integer or decimal for each matrix element.)
Answers
The probability that state 1 changes to state 2 after three repetitions of the experiment is 0.052.
The first power of the transition matrix A is simply the matrix itself:
A1 = [ 0.3 0.1 0.6 ]
[ 0.5 0.2 0.3 ]
The second power of the transition matrix is obtained by multiplying A by itself:
A2 = A1 * A1 = [ 0.30.3+0.10.5 0.30.1+0.10.2 0.30.6+0.10.3 ]
[ 0.50.3+0.20.5 0.50.1+0.20.2 0.50.6+0.20.3 ]
= [ 0.19 0.06 0.33 ]
[ 0.29 0.08 0.33 ]
The third power of the transition matrix is obtained by multiplying A2 by A:
A3 = A2 * A = [ 0.190.3+0.060.5 0.190.1+0.060.2 0.190.6+0.060.3 ]
[ 0.290.3+0.080.5 0.290.1+0.080.2 0.290.6+0.080.3 ]
= [ 0.161 0.052 0.327 ]
[ 0.247 0.068 0.327 ]
To find the probability that state 1 changes to state 2 after three repetitions of the experiment, we need to look at the second element of the first row of A3. This element is 0.052, so the probability that state 1 changes to state 2 after three repetitions of the experiment is 0.052.
To know more about probability visit :
brainly.com/question/30034780?referrer=searchResults
#SPJ4
For the function f(x)=x+4−−−−−√
, the average rate of change to the nearest hundredth over the interval 2 ≤ x ≤ 6 is
Answers
The average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6 is approximately 0.29 to the nearest hundredth.
To find the average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6, we need to calculate the change in the function divided by the change in the input variable over that interval.
The change in the function between x = 2 and x = 6 is:
f(6) - f(2) = √(6+4) - √(2+4) = √10 - √6
The change in the input variable between x = 2 and x = 6 is:
6 - 2 = 4
So, the average rate of change of the function over the interval 2 ≤ x ≤ 6 is:
(√10 - √6) / 4
To approximate the answer to the nearest hundredth, we can use a calculator or perform long division to get:
(√10 - √6) / 4 ≈ 0.29
For such more questions on function
https://brainly.com/question/11624077
#SPJ8
what are the x intercepts of y=4x^2-12x+4
Answers
The x-intercepts of the given equation 4x^2-12x+4 is -3/2
What is Quadratic equation ?
Quadratic equation can be defined as the equation in which it is in the form of ax^2+bx+c = 0
where c is a constant.
Given equation ,
y = 4x^2+12x+4
so we have to find the x-intercept , make y = 0
and we have to solve for the given quadratic equation
so,
we get
4x^2+12x+4 = 0
(2x)^2 + 9 + 12x = 0
(2x+3)^2 = 0
x = -3/2
There is double root unique intercept or tangent at x = -3/2
Therefore, The x-intercepts of the given equation 4x^2-12x+4 is -3/2
To learn more about Quadratic equation from the given link.
https://brainly.com/question/30098550
#SPJ1
Find the length of the missing side.
14.5 m
7.3 m
X

Answers
Answer:
x= 12.528
*rounded is 12.53 or 12.5
Step-by-step explanation:
7.3 ^2 + x^2 = 14.5^2
53.29 + x^2 = 210.25
-53.29 -53.29
x^2= 156.96
x= 12.528
Use the graph below to find the following:
A) what is the slope of the line?
B) what is the y intercept of the line?
C) what is the equation of the line in slope intercept form?

Answers
B.) The y-intercept is b=-5
C.) The equation is: y=-2x-5
Find the odd one out 1.234,
123.4 hundredths,
1234 thousandths,
12.34,
123 hundredths and 4 thousandths
Answers
The decimal odd one out is: 123 hundredths and 4 thousandths.
What are decimals?The accepted method for representing both integer and non-integer numbers is the decimal numeral system. It is the expansion of the Hindu-Arabic numeral system to non-integer values.
Decimal notation is the term used to describe the method of representing numbers in the decimal system.
Given: 1.234 is a decimal.123.4 hundredths, 1234 thousandths and 12.34 are all different forms of the given decimal. But 123 hundredths and 4 thousandths is not.
This is due to the fact that in the other selections, it is written in decimal format or is finished, but in the fourth or final option, it is purposefully not written in decimals. It is hence the outlier.
Hence, The decimal odd one out is: 123 hundredths and 4 thousandths.
To learn more about decimals, refer to the link: https://brainly.com/question/703656
#SPJ9
The area of a square is 36 sq.cm, then its perimeter is a) 24 cm b) 6 cm c) 144 cm d) 36 cm
Answers
Answer:
Step-by-step explanation:
3.6*
It is very easy to find the perimeter of a square when its area is given in the question. For that, you only ned to know one fomula. That formula is: Area = side^2
For this particular question, the given value for the area of the square is 36 sq.cm. So, we can solve for the side(s) by substituting the given value in the above mentioned formula.
We get
36 = s^2
Now, we need to get the square root of both sides, which gives us
s = √36 s = 6 cm
Since all the sides of a square are equal in length, the side length is 6 cm. Now to determine the perimeter, we must multiply the side length by 4 (because there are 4 equal sides in a square). That gives us Perimeter = 4 x side length Perimeter = 4 x 6 cm.
Therefore, the perimeter of the square is 24 cm.
Check this out-
https://brainly.com/question/29192128?referrer=searchResults
1/8 of the toys in a play area are yellow, and 1/4 are green. 3/5 of the remainder are red. The rest of the toys are blue. If there are 100 green toys, how many blue toys are there?
Answers
A fraction is a fragment of a whole number, used to define parts of a whole. The whole can be a whole object, or many different objects. The number at the top of the line is called the numerator, whereas the bottom is called the denominator.
To figure out what fraction of the toys are blue, we need to convert all of the fractions to have a common denominator.
What is a common denominator?A common denominator consists of two or more fractions that have the same denominator. This makes it easier to perform numeric equations, and to solve them.
Looking at the fractions, we can see that there are 3 fractions, \(\frac{1}{8}, \frac{1}{4}\) and \(\frac{3}{5}\).
To solve for the common denominator between \(\frac{1}{8}\) and \(\frac{3}{5}\), we first multiply the denominators, 8 and 5.
8 × 5 = 40We now know that the denominator is going to be 40.
\(\frac{?}{40} \frac{?}{40}\)To get the numerators, we can use these equations:
1 × 5 = 58 × 3 = 24The new fractions look like this:
\(\frac{5}{40} \frac{24}{40}\)To easily convert the last fraction (\(\frac{1}{4}\)) we can multiply the numerator and denominator by 10.
1 × 10 = 104 × 10 = 40Why do we multiply by 10?We multiply by 10 because the denominator, which is 4, can be multiplied by 10 to get our common denominator of 40.
Now, we have our 3 fractions converted to have common denominators.
(\(\frac{5}{40}, \frac{24}{40}\) and \(\frac{10}{40}\))
(Yellow, red, and green)
We can now add these up and see what fraction of blue is remaining.
\(\frac{5}{40}+ \frac{24}{40}+ \frac{10}{40} =\frac{39}{40}\)\(1 - \frac{39}{40} = \frac{1}{40}\)Therefore, the fraction of blue toys compared to the total amount is \(\frac{1}{40}\).
If there are 100 green toys resulting in \(\frac{10}{40}\) of all the toys, we can divide 100 by 10 to get the number of blue toys.
Why do we divide by 10?We divide by 10 because \(\frac{1}{40}\) is only \(\frac{1}{10}\) of \(\frac{10}{40}\), meaning we divide by 10.
100 ÷ 10 = 10Therefore, there are 10 blue toys.
Answer:
1/4=100
10/40=100
40/40=400
1/8=400/8=50
3/5=400/5*3=240
400-100-50-240=10
10 of the toys are blue
Hope this helped!!
Step-by-step explanation:
The length of a rectangular garden is 5 feet less than 4 times its width. Its area is 359 square feet. Find the length and width of the garden. Round answers to the nearest tenth of a foot. Show all work.
Answers
Given parameters:
Area of the rectangular garden = 359ft²
Unknown:
length and width of the garden = ?
To find the length and breadth of the garden, we need to define and know that the area of a rectangle is.
Area of a rectangle = Length x Breadth
From the problem statement;
Let w = width of the rectangular garden
L = length of the garden;
Now,
length of a rectangular garden is 5 feet less than 4 times its width
L = 4w - 5
Now let us substitute this into the equation;
Area = L x w
359 = (4w - 5)w
4w² - 5w - 359
Using:
w = -b ± √b² - 4ac / 2a
where b = -5 , a = 4 and c = -359
w = -(-5) ± √-5² - 4(4)(-359) / 2(4)
w = 5 ± √25 + 5744 / 8
w = 5 ± 75.9 / 8
w = \(\frac{5 + 75.9}{8} or \frac{5 - 75.9}{8}\)
w = 10.1ft
The other solution is not possible it will be a negative value. Width value cannot be negative.
So L = 4w - 5 = 4(10.1) - 5 = 35.5ft
The length and breadth of the rectangular are 35.5ft and 10.1ft respectively.
Simplify 5-(6a-3b-8)
Answers
Answer:
Step-by-step explanation:
5- (6a-3b-8) BODMAS
-30a-15b-40
What is the gravitational force on a 35.0 kg object standing on the Earth’s surface?
Answers
Answer:341.97 N
Step-by-step explanation:Answer and Explanation: The gravitational force on the 35 kg mass at the surface of the Earth is 341.97 N while at the surface of the Moon the 35 kg mass feels only 57.56 N. The gravitational force on the surface of the Earth is 5.94 times greater than that of the surface of the moon.
A student is solving the problem
x^2 + 10x + _ = 16 + _
by method of completing the square. What number should the student add to both sides?
A. 4
B. 16
C. 25
D. 5
Answers
We should add 25 both side by method of completing the square.
We have to given that;
A student is solving the problem
x² + 10x + _ = 16 + _
Now, We can completing the square as;
⇒ x² + 10x + 5² = 16 + 5²
⇒ x² + 10x + 25 = 16 + 25
⇒ (x + 5)² = 16 + 25
Hence, We should add 25 both side by method of completing the square.
Learn more about the quadratic equation visit:
brainly.com/question/1214333
#SPJ1
2x + y = 7
x + y = 1
Answers
The solution to the system of equations is x = 6 and y = -5, which is the same as we obtained using the elimination method.
What is the system of equations?A system of equations is a collection of one or more equations that are considered together. The system can consist of linear or nonlinear equations and may have one or more variables. The solution to a system of equations is the set of values that satisfy all of the equations in the system simultaneously. The given system of equations is:
2x + y = 7 ---(1)
x + y = 1 ---(2)
To solve this system, we can use the method of elimination or substitution.
Method 1: Elimination
In this method, we eliminate one of the variables by adding or subtracting the two equations. To do this, we need to multiply one or both equations by a suitable constant so that the coefficients of one of the variables become equal in magnitude but opposite in sign.
Let's multiply equation (2) by -2, so that the coefficient of y in both equations becomes equal in magnitude but opposite in sign:
-2(x + y) = -2(1) --
Multiplying equation
(2) by -2-2x - 2y = -2
Now we can add the two equations (1) and (-2x - 2y = -2) to eliminate y:
2x + y = 7(-2x - 2y = -2)0x - y = 5
We now have a new equation in which y is isolated.
To solve for y, we can multiply both sides by -1:
-1(-y) = -1(5)y = -5
Now that we know y = -5, we can substitute this value into equation (2) to find x:x + y = 1x + (-5) = 1x = 6
Therefore, the solution to the system of equations is (x,y) = (6,-5).
Method 2: Substitution
In this method, we solve one of the equations for one variable in terms of the other variable and substitute this expression into the other equation to get an equation with only one variable.
From equation (2), we can solve for y in terms of x:y = 1 - x
We can then substitute this expression for y into equation (1):2x + y = 72x + (1 - x) = 7 --Substituting y = 1 - xx + 1 = 7x = 6
Now that we know x = 6, we can substitute this value into equation (2) to find y:x + y = 16 + y = 1 --Substituting x = 6y = -5
Therefore, the solution to the system of equations is (x,y) = (6,-5), which is the same as we obtained using the elimination method.
To learn more about the system of equations visit:
brainly.com/question/25976025
#SPJ1
Find the interest.
. 750$, 6.5%, 2years
Answers
Answer:
simple interest=$97.50.
compound interest= $100.668
Step-by-step explanation:
Given:
Principal (P) = $750
Rate (R) = 6.5% (in decimal form, 0.065)
Time (T) = 2 years
Simple Interest = Principal*Rate*Time
Using the formula, the simple interest is calculated as follows:
Simple Interest = $750*0.065*2 = $97.50
Therefore, the simple interest for $750 with a 6.5% interest rate over 2 years is $97.50.
Again:
Compound Interest = Principal*(1 + Rate)^(Time)-Principal
Using the same values as above, the compound interest can be calculated as follows:
Compound Interest = $750*(1+0.065)^(2)-$750
= $750*1.065^2 -$750
= $750 × 1.134225 - $750
= $850.66875-$750
= $100.668
Therefore, the compound interest for $750 with a 6.5% interest rate over 2 years is $100.668
A police checkpoint is set up on New Years Eve to catch drunk drivers. It is known that 8% of drivers on New Years Eve have a blood-alcohol level that is above the legal limit. It is also known that 32% of drivers in the area never drink and drive, but are simply bad drivers. The remaining 60% of drivers never drink and drive and are good drivers. At this particular checkpoint, the police stop 85% of the drunk drivers, stop 38% of the bad drivers, and stop 2% of the good drivers. (a) There are four key events in this problem. Specify the four key events and define notation for each of them. (b) What is the probability that a randomly selected driver will be stopped at the checkpoint? (c) What is the probability that a driver who is stopped at the checkpoint is drunk?
Answers
Answer:
(a) Let the probability drivers are drunk = P(D) = 0.08
The probability that drivers in the area never drink and drive, but are simply bad drivers = P(B) = 0.32
The probability that drivers in the area never drink and drive, and are good drivers = P(G) = 0.60
Let S = event that the police stops the driver.
(b) The probability that a randomly selected driver will be stopped at the checkpoint is 0.2016.
(c) The probability that a driver who is stopped at the checkpoint is drunk is 0.337.
Step-by-step explanation:
We are given that 8% of drivers on New Years' Eve have a blood-alcohol level that is above the legal limit. It is also known that 32% of drivers in the area never drink and drive, but are simply bad drivers. The remaining 60% of drivers never drink and drive and are good drivers.
At this particular checkpoint, the police stop 85% of the drunk drivers, stop 38% of the bad drivers, and stop 2% of the good drivers.
(a) Let the probability drivers are drunk = P(D) = 0.08
The probability that drivers in the area never drink and drive, but are simply bad drivers = P(B) = 0.32
The probability that drivers in the area never drink and drive, and are good drivers = P(G) = 0.60
Let S = event that the police stops the driver
These are the four events stated in the question.
(b) So, the probability that the police stop the drunk drivers = P(S/D) = 0.85
The probability that the police stop the bad drivers = P(S/B) = 0.38
The probability that the police stop the good drivers = P(S/G) = 0.02
Now, the probability that a randomly selected driver will be stopped at the checkpoint is given by = P(S)
P(S) = P(D) \(\times\) P(S/D) + P(B) \(\times\) P(S/B) + P(G) \(\times\) P(S/G)
= (0.08 \(\times\) 0.85) + (0.32 \(\times\) 0.38) + (0.60 \(\times\) 0.02)
= 0.068 + 0.1216 + 0.012
= 0.2016
Hence, the probability that a randomly selected driver will be stopped at the checkpoint is 0.2016.
(c) Now, the probability that a driver who is stopped at the checkpoint is drunk is given by = P(D/S)
P(S/W) = \(\frac{P(D) \times P(S/D)}{P(D) \times P(S/D)+P(B) \times P(S/B)+P(G) \times P(S/G)}\)
= \(\frac{0.08\times 0.85}{0.08\times 0.85+0.32\times 0.38+0.60\times 0.02}\)
= \(\frac{0.068}{0.2016}\) = 0.337
Hence, the probability that a driver who is stopped at the checkpoint is drunk is 0.337.
A class counts how many vehicles drove past their school from 1:00pm to 2:00pm. There's 3 times as many cars as trucks
Answers
Factor problems 9 - 12 by using the difference of squares method.
9. x2 – 4
A. This polynomial cannot be factored by using the difference of squares method.
B. (x – 2)(x – 2)
C. (x – 2)(x – 1)
D. (x – 2)(x + 2)
E. (x – 1)(x – 4)
F. (x + 2)(x + 2)
10. x2 – 25
A. (-x – 5)(x - 5)
B. This polynomial cannot be factored by using the difference of squares method.
C. (-x + 5)(x + 5)
D. (x – 5)(x + 5)
E. (x + 5)(-x - 5)
F. (x – 5)(x - 5)
11. 36x4 – 4x2
A. (6x2 – 2x)(6x2 - 2x) = 4x2(3x - 1)(3x - 1)
B. (6x2 + 2x)(6x2 + 2x) = 2x2(3x + 1)(2x + 1)
C. This polynomial cannot be factored by using the difference of squares method.
D. (-6x2 – 2x)(-6x2 - 2x) = 4x2(-3x - 1)(-3x - 1)
E. (6x2 – 2x)(6x2 + 2x) = 4x2(3x - 1)(3x + 1)
F. (-6x2 + 2x)(6x2 - 2x) = 2x2(-3x + 1)(3x - 1)
12. x2 + 100
A. (x + 10)(x – 10)
B. (-x + 10)(x – 10)
C. (x + 10)(x + 10)
D. This polynomial cannot be factored by using the difference of squares method.
E. (x - 10)(x – 10)
F. (-x + 10)(-x – 10)
Answers
Answer:
Step-by-step explanation:
9. D
10.D
11.E
12.D
Answer:
9.
\(x^2-4\\(x-2)(x+2)\)
10.
\(x^2-25\\(x-5)(x+5)\)
11.
\(36x^4-4x^2\\4x^2(9x^2-1)\\4x^2(3x+1)(3x-1)\)
12.
\(x^2+100\\\)
This polynomial cannot be factored by using the difference of squares method
Consider a binomial experiment with n = 9 trials where the probability of success on a single trial is p = 0.40. (For each answer, enter a number. Round your answers to three decimal places.)
(a) Find P(r = 0).
(b) Find P(r ≥ 1) by using the complement rule.
Answers
The probability a ) P ( r = 0 ) = 0.010 and b ) P ( r \(\geq\) 1 ) = 0.99 .
The binomial distribution formula is:
P ( r successes in n trials ) = [ nCr ] * [ p^r ] * [ q ^ ( 1 - r ) ]
where [ nCr ] is the number of combinations of number of objects g taken r at a time, p is probability of success & (1-p) ie. q is the probability of failure.
We are given p = 0.40
n = 9
a) P ( r = 0 ) = 9C0 x 0.40^0 x (0.6)^9 = 1 * 1 * 0.010 = 0.010
b) P( r ≥ 1 ) = 1 - Pr ( r = 0 ) = 1 - 0.010 = 0.99
To learn more on binomial distribution follow link :
https://brainly.com/question/9325204
#SPJ9
Pls help us with the math Thank you

Answers
total no. of tins = 21
no. of tins given to one man = 21/3 = 7 tins
total paint (taking full tin as y) = 7y +(½ × 7 y)
= 7y + 3.5 y = 10.5 y
amount of paint given to one man in terms of y = 10.5 y / 3
= 3.5y
so
man 1 will recieve 3 full tins and a ½ full tin
man 2 will recieve 3 full tins and a ½ full tin
man 3 will recieve 1 full tin and a 5 ½ tins
each man now have recieved equal amount of paint but not tins since we didn't distribute the empty tins let's distribute it such that each man in total ( including filled tins) recieve 7 tins
then your answer is
man 1 will recieve 3 full tins , a ½ full tin and 3 empty tins.
man 2 will recieve 3 full tins , a ½ full tin and 3 empty tins.
man 3 will recieve 1 full tin , 5 ½ tins and 1 empty tin.
attached a written working as well :)
hope you understood
mark as brainliest please
5a. find the value of a.

Answers
The logarithmic function f(x) = a·log₃(x - 4), passing through the points (13, 7), has the values;
5 a. The value of a is 3.5
b. Please find attached the graph of the function, f(x) = 3.5·log₃(x - 4), created with MS Excel
What is a logarithmic function?A logarithmic function is a function that contain and involves logarithm operation and it is the inverse of an exponential function
The function is f(x) = a·log₃(x - 4),
x > 4 and a > 0
The coordinates of a point on the graph of the function, f is A(13, 7)
5 a. The value of a can be found by plugging in the value of (13, 7) = (x, f(x)), as follows
f(13) = 7 = a·log₃(13 - 4) = a·log₃9 = a·log₃3²
7 = a·log₃3²
7 = 2·a·log₃3 = 2·a·1 = 2·a
2·a = 7
a = 7 ÷ 2 = 3.5
a = 3.5
5 b. The coordinates of the x-intercept of the graph = (5, 0)
The equation of the function is;
f(x) = 3.5·log₃(x - 4)
A third point on the graph is given when f(x) = 14 as follows;
f(x) = 14 = 3.5·log₃(x - 4)
log₃(x - 4) = 14 ÷ 3.5 = 4
3⁴ = x - 4
x = 3⁴ + 4 = 85
Which gives the point, (85, 14)
Similarly, we have the point (31, 10.5), (7, 3.5)
Please find attached the graph of f(x) created with MS Excel
Learn more about logarithmic functions here:
https://brainly.com/question/28033379
#SPJ1

plase help 50 points

Answers
2. 21
3. 161
4.156
4) Students in Ms. Udon
science class planted 13
conifers in different places
around the school yard. They
measured the heights (in inches)
of the conifers one month after
planting them. How many
conifers are greater than 6 1/4
inches tall but less than 8 1/2
inches tall?
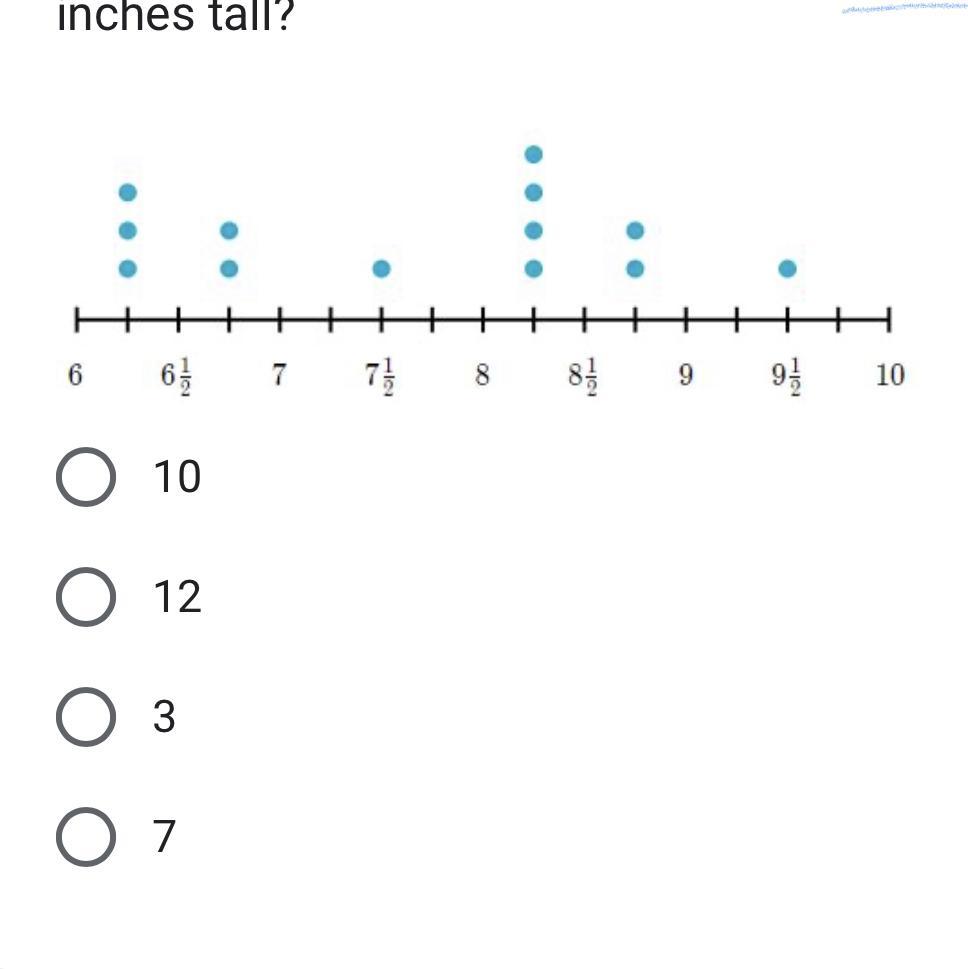
Answers
Considering the dot plot, the tallest conifer is 3.25 inches taller than the shortest conifer.
This shows, with dots, the number of times that each of the measures appears in a data set.
For finding the dot plot, we have that:
The shortest conifer measures 6 and 1/4
= 6.25 inches.
The tallest conifer measures 9.5 inches.
The difference is:
9.5 - 6.25 = 3.25 inches.
Therefore the tallest conifer is 3.25 inches taller than the shortest conifer.
More can be learned about a dot plot at;
brainly.com/question/24912483
#SPJ1
Top
Which of the numbers given are rational?
Select all that apply:
√3300
2.6228
4.137183
√9
9.327925...
Answers
From the given numbers, 2.6628, 4.17183 and √9 are the rational numbers.
Rational numbers are the numbers that are in the form of p/q where q is not equal to zero that is q≠0. Rational numbers can be expressed as a fraction where both numerators and denominator are whole. When these fractions are further divided, the result will be in decimal form, which may be either terminating decimal or the repeating decimal
Irrational numbers are numbers that cannot be written as simple fractions but can be written in decimal form. It has endless non-terminating digits after the decimal point.
Now according to the question ,
i) √3300 = 57.4456…. as it has endless non-terminating digits after the decimal point. It is an irrational number.
ii) 2.6628 is a rational number as it has a terminating decimal.
iii) 4.137183 is also a rational number as it has terminating decimal.
iv) √9 = 3 is a rational number as it is a perfect square and can be written as fraction.
v) 9.327925…. is a irrational as it has endless non-terminating digits after the decimal point.
Hence 2.6628, 4.17183 and √9 are the rational numbers.
Learn more about rational numbers here : https://brainly.com/question/43641
#SPJ9