Solve 3(x + 2) >x
Please
Answers
Answer:
x > −3
Step-by-step explanation:
Let's solve your inequality step-by-step.
3(x + 2) > x
Step 1: Simplify both sides of the inequality.
3x + 6 > x
Step 2: Subtract x from both sides.
3x + 6 − x > x − x
2x + 6 > 0
Step 3: Subtract 6 from both sides.
2x + 6 − 6 > 0 − 6
2x > −6
Step 4: Divide both sides by 2.
2x / 2 > −6 / 2
x > −3
Answer:
x > −3
Hope this helps :)
Related Questions
21. Graph the quadratic function f(x) = 2(x + 4)²-1. Find and label the vertex and axis of symmetry. Vertex Axis of symmetry.
Answers
Answer:Pitch of the sound depends upon its frequency. As the pitch of the sound is directly proportional to frequency, Low-frequency sounds are said to have low pitch whereas sounds of high frequency are said to have the high pitch.
Step-by-step explanation:
Identify the slope and y-intercept of the line. y = 4x − 11
slope=
y-intercept (x, y) =
Answers
Step-by-step explanation:
Equation of a line is y = mx + c
where
m is the slope
c is the y intercept
From the question the equation is
y = 4x − 11
Comparing with the general equation above
Slope = 4y - intercept = - 11 or ( 0 , - 11)Hope this helps you
College Algebra Applied Problem Four A medical professional is helping an individual balance their diet. The individual has asked for some certain foods to remain in their diet. They will always get 600 calories from carbohydrates. The individual says that they can be flexible about how many calories they consume in fats and proteins. The goal of the diet is to keep the individual at 1,800 calories per day ( 600 of which come from carbohydrates). Part One Write an equation that models the amount of calories from fats " f ' and protein "p" that the individual can consume in order to reach 1,800 calories. Part Two The diet being prescribed to the individual calls for calories from protein to be three times the calories from fat. Write an equation based on this information that relates calories from protein "p" to calories from fat " f ". Part Three Use your equations from parts "b" and "c" to solve this system of equations and determine the amount of calories that the individual should consume from fats and proteins. Part Four If the individual no longer required 600 calories from carbohydrates, and instead said that they would be flexible about how many carbohydrates they would consume, how many variables would there be for this problem on calories?
Answers
The system equation that models the amount of calories from fats (f) and proteins (p) that the individual can consume to reach 1,800 calories is: f + p = 1,200. The equation that relates calories from protein (p) to calories from fat (f) based on the prescribed diet is: p = 3f. Solving the system of equations, we find that the individual should consume 300 calories from fats and 900 calories from proteins.
To find the equation that models the amount of calories from fats and proteins that the individual can consume in order to reach 1,800 calories, we consider that 600 calories will come from carbohydrates. Since the total goal is 1,800 calories, the remaining calories from fats and proteins should add up to 1,800 - 600 = 1,200 calories. Therefore, the equation is f + p = 1,200.
Based on the prescribed diet, the individual is required to consume calories from protein that are three times the calories from fat. This relationship can be expressed as p = 3f, where p represents the calories from protein and f represents the calories from fat.
To solve the system of equations, we substitute the value of p from the second equation into the first equation: f + 3f = 1,200. Combining like terms, we get 4f = 1,200, and dividing both sides by 4 yields f = 300. Substituting this value back into the second equation, we find p = 3(300) = 900.
Therefore, the individual should consume 300 calories from fats and 900 calories from proteins to meet the diet requirements and achieve a total of 1,800 calories.
Learn more about system equation
brainly.com/question/32645146
#SPJ11
Indicate in standard form the equation of the line through the given points, writing the answer in the equation box
below.
PO.-4). Q15, 1)

Answers
Answer:
y = x-4
Step-by-step explanation:
The standard form is;
y = mx + b
where m is the slope and b is the y-intercept
we have the two points as (0,-4) and (5,1)
so we find the slope using the slope formula;
m = (y2-y1)/(x2-x1)
m = (1 + 4)/(5-0) = 5/5 = 1
The y-intercept value is the value of y when x = 0
We already have a point (0,-4) and the equation would be:
y = 1(x) + (-4)
y = x-4
Convert 2.25 to a mixed number and an improper fraction. Write answers in the simplest form.
Answers
Answer: Answer in picture
Step-by-step explanation:
Math

HELP PLEASEEE
PLEASEEEEEEEEEEEEEEEEEEEEEEe


Answers
I did this some point September my teacher was getting up ready
Identify the shapes in the picture
Answers
Answer:
we're are the images pls
If the length of the base of a triangle is 7 m and the area of this triangle is 56 square meters, what is the length of the height of this triangle?
Answers
Answer:
treatment iijiijiuej325ufffufuvufuuuuuuuuuuuuuu
Answer:
16m
Step-by-step explanation:
Using the formula A=h_b*b/2
56=h_7*7/2
h_7*7=112
divide both sides by 7
h_7=16
In how many different ways can we sit n people around a round table? The sits are indistinguishable but the relative position of people is not. 3. A license plate can have four one-digit numbers or two one-digit numbers and two letters. How many different license plates are there?
Answers
There are 686,000 different license plates.
To solve this problem, we can fix one person's position and arrange the remaining (n-1) people around the table.
Since the seats are indistinguishable, we divide the total number of arrangements by n to avoid counting duplicate arrangements.
The number of different ways to sit n people around a round table is (n-1)!.
A license plate can have four one-digit numbers or two one-digit numbers and two letters.
For the first case, where the license plate has four one-digit numbers, there are 10 choices for each digit (0-9).
Therefore, there are 10 choices for the first digit, 10 choices for the second digit, 10 choices for the third digit, and 10 choices for the fourth digit. In total, there are 10^4 = 10,000 different license plates.
For the second case, where the license plate has two one-digit numbers and two letters, there are 10 choices for each digit and 26 choices for each letter (assuming only uppercase letters).
Therefore, there are 10 choices for the first digit, 10 choices for the second digit, 26 choices for the first letter, and 26 choices for the second letter. In total, there are 10^2 * 26^2 = 676,000 different license plates.
Different license plate = 10,000 + 676,000
= 686,000
learn more about license from given link
https://brainly.com/question/2128824
#SPJ11
B. Prove the following using indirect proof.
1. If x = 3, then 3x + 5 ≠10
2. If a triangle is an isosceles triangle ( 2 sides are equal), then the base angles
cannot measure 92 degrees.
3. Given: 3 - 5 ≠ 13
Prove: r≠6
4.Given: x = 5
Prove: 2x + 4 12
Answers
Answer:
jsjsusjsksksisidjjdsksjks
Rowan has $60. He wants to leave a 20% tip on his restaurant bill. His restaurant bill is $52.22.
Answers
Answer:
Step-by-step explanation:
20% tip on 52.22 is 10.44
52.22*0.2=10.44
I don't think he has enough to do it though
52.22+10.44=62.664
Answer: He doesn't have enough (2.66 dollars short) Max percentage: 14.9%
Step-by-step explanation:
If Rowan has $60 dollars and wants a 20% tip. He would need to multiply the restaurant bill by 6/5, of if easier 120%
$52.22 x 120% = 62.66 dollars.
62.66 - 60 = 2.66. Therefore, Rowan CANNOT pay off a 20% tip and has $2.66 short.
Now, if we wanted to calculate which percent he can pay at max we look at 60/52.22.
This will give us 1.14898. Because of this, we can determine what percent Rowan can pay at max. 1.14898 - 1 = 0.14898.
Therefore, converting to percent, he can pay 14.9%(rounded)
what is 4876398 -742 x 2+4769-1
Answers
Answer: 4,879,682
Step-by-step explanation:
Answer:
4,879,682
Step-by-step explanation:
Casper collected 108 old baseball cards. He then bought new baseball cards to increase his collection by 25%. How many new baseball cards did he buy?
Answers
Answer:
27
Step-by-step explanation:
what I did is used a calculator and did 108 x 0.25 (25% as a decimal)
biologists stocked a lake with fish and estimated the carrying capacity to be . the number of fish grew to 1100 in the first year. round to 4 decimal places. a) find an equation for the fish population, , after years.
Answers
An equation for the fish population, after years is P(t) ≈ 8000e-0.664t ± 0.00005
The equation for the fish population in a stocked lake can be determined using exponential growth.
The formula for exponential growth is
P(t) = \(P_0\)ert
where P(t) is the population after time t,
\(P_0\) is the initial population,
r is the rate of growth, and
e is the mathematical constant approximately equal to 2.71828.
The carrying capacity, K, is the maximum population that can be supported by the environment, and it is a limiting factor for population growth. When the population reaches K, the growth rate slows down until it reaches a point of equilibrium.
The carrying capacity can be estimated using a variety of methods, including the logistic model, which incorporates the carrying capacity into the equation for population growth.
However, for this problem, we are given an estimate of the carrying capacity, which we will use in the exponential growth equation.
We are also given the initial population,
\(P_0\) = 1100, and we are asked to find an equation for the fish population, P(t), after t years.
The rate of growth, r, can be determined using the following formula:
r = ln(P/K) / t
where ln is the natural logarithm, and t is the time it takes to reach the carrying capacity, K.
Since we don't have an exact value for K, we will use the estimated value of 8000.
Thus,
r = ln(1100/8000) / 1
r ≈ -0.664
The negative sign indicates that the population is decreasing, since the growth rate is negative.
Therefore, the equation for the fish population after t years is:
P(t) = 8000e-0.664t
To round to 4 decimal places, we can use the formula:
P(t) ≈ 8000e-0.664t ± 0.00005
For similar question on equation
https://brainly.com/question/2972832
#SPJ11
A fruit juice recipe uses three ingredients. Two of the ingredients use a ratio of 2 ounces of pineapple juice to 5 ounces of fruit punch. Part A: Grape a line on the coordinates plane to represent this relationship
Part B: Create an equation to represent this relationship. Let x represent ounces of pineapple juice. Let y represent ounces of fruit punch.
Answers
Answer:
(a) See attachment
\((b)\ y =2.5x\)
Step-by-step explanation:
Given
\(x \to pineapple\)
\(y \to fruit\)
\(x : y =2 : 5\)
Solving (a): The graph
First, we create an equation from \(x : y =2 : 5\)
Express as fraction
\(\frac{x }{ y} =\frac{2 }{ 5}\)
Cross multiply
\(2y = 5x\)
See attachment for graph
Solving (b): An expression that represents the relationship
In (a), we have:
\(2y = 5x\)
Divide by 2
\(y = \frac{5}{2}x\)
\(y =2.5x\)

It must be in a fraction and a equation to find the amount of time the dough rises in the bowl.

Answers
The amount of time spent in the bowl is 1 1/4 hours
How to determine the amount of time spent in the bowlFrom the question, we have the following parameters that can be used in our computation:
Total time = 1 1/2 hours
Time to rise = 1/4 hour
This means that
Time spent in the bowl = Total time - Time to rise
Substitute the known values in the above equation, so, we have the following representation
Time spent in the bowl = 1 1/2 - 1/4
Evaluate the like terms
Time spent in the bowl = 1 1/4
Hence, the time is 1 1/4 hours
Read more about fractions at
https://brainly.com/question/2929160
#SPJ1
The numerical value of standard deviation can never be______
Answers
The standard deviation lies in the range of 0 to 1. The numerical value of standard deviation can never be negative.
The standard deviation is a measure of amount of variation or dispersion of a set of values. When we compare two unequal observations, the result is always greater than zero i.e., always positive.
Standard deviation is the square root of the variance of the observations and the root always gives values either positive or zero, it can never be negative.
Therefore, the numerical value of the standard deviation can be positive. The value of standard deviation is always greater or equal to zero.
To know more about standard deviation.
https://brainly.com/question/17084031
#SPJ4
The vertical supports in this subdivided truss bridge are built
so that ayb-xyz in the ratio 1:3. if ay= 4 meters,
what is xy
Answers
The value of xy in the given ratio is 12 meters, which suggests that xy is a product of two quantities.
Based on the given information, the ratio between ay and xy is 1:3. We know that ay = 4 meters. Let's find the value of xy. If the ratio between ay and xy is 1:3, it means that ay is one part and xy is three parts. Since ay is 4 meters, we can set up the following proportion:
ay/xy = 1/3
Substituting the known values:
4/xy = 1/3
To solve for xy, we can cross-multiply:
4 * 3 = 1 * xy
12 = xy
To know more about value,
https://brainly.com/question/21727232
#SPJ11
Based on the given information and using the ratio, we have found that xy is equal to 12b, where b represents an unknown value. The exact length of xy cannot be determined without additional information.
The ratio between ayb and xyz is given as 1:3. We know that ay has a length of 4 meters. To find the length of xy, we can set up a proportion using the given ratio.
The ratio 1:3 can be written as (ayb)/(xyz) = 1/3.
Substituting the given values, we have (4b)/(xy) = 1/3.
To solve for xy, we can cross-multiply and solve for xy:
3 * 4b = 1 * xy
12b = xy
Therefore, xy is equal to 12b.
It's important to note that without additional information about the value of b or any other variables, we cannot determine the exact length of xy. The length of xy would depend on the value of b.
Learn more about ratios and proportion
https://brainly.com/question/26974513
#SPJ11
Wendell is looking over some data regarding the strength, measured in Pascals (Pa), of some building materials and how the strength relates to the length. The data are represented by the exponential function f(x) = 2x, where x is the length. Explain how he can convert this equation to a logarithmic function when strength is 8 Pascals.
Answers
x = ㏑₂8 in the logarithmic function.
What is a logarithmic function?A logarithmic function is the inverse of an exponential function.
Given function if f(x) = \(2^{x}\),
When strength is equal to 8 pascals, f(x) = 8
Therefore, 8 = \(2^{x}\)
Taking log on both sides:
ln8 = ln\(2^{x}\)
ln8 = xln2
or x = ln8/ln2
x = ㏑₂8
Hence, the required function is x = ㏑₂8.
To learn more about logarithmic functions visit:
https://brainly.com/question/10042160
#SPJ1
28. Given M₁ = 35, M₂ = 45, and SM1-M2= 6.00, what is the value of t? -2.92 -1.67 O-3.81 2.75
Answers
The t-distribution value is -1.67 for the given mean samples of 35 and 45. Thus, option B is correct.
M₁ = 35
M₂ = 45
SM1-M2 = 6.00
The t-value or t-distribution formula is calculated from the sample mean which consists of real numbers. To calculate the t-value, the formula we need to use here is:
t = (M₁ - M₂) / SM1-M2
Substituting the given values into the formula:
t = (35 - 45) / 6.00
t = -10 / 6.00
t = -1.67
Therefore, we can conclude that the value of t is -1.67 for the samples given.
To learn more about t-distribution value
https://brainly.com/question/30701897
#SPJ4
The t-distribution value is -1.67 for the given mean samples of 35 and 45. Thus, option B is correct.
Given, M₁ = 35
M₂ = 45
SM1-M2 = 6.00
The t-value or t-distribution formula is calculated from the sample mean which consists of real numbers.
To calculate the t-value,
the formula we need to use here is:
t = (M₁ - M₂) / SM1-M2
Substituting the given values into the formula:
t = (35 - 45) / 6.00
t = -10 / 6.00
t = -1.67
Therefore, we can conclude that the value of t is -1.67 for the samples given.
To learn more about t-distribution value here:
brainly.com/question/30701897
#SPJ4
Determine the solution set 2x+3(4-x)≤x<2(x+1)
Answers
Answer:
6≤x>2
Step-by-step explanation:
2x+3(4-x)≤x<2(x+1) simplify
2x+12-3x≤x<2x+2
first step:
-x+12≤x
-x+12+x≤x+x
12≤2x , then 12/2 ≤ x
6≤x or x ≥ 6
second step: x<2x+2
x-2x<2x-2x+2
-x<2 when divide by negative the sign flip in this case from less to great than
x>2
6≤x>2
what is the probability (in percentage) that a score will fall between a -3z and +2 z scores?
Answers
The probability (in percentage) that a score will fall between a -3z and +2 z scores is 97.59%.
Assuming a standard normal distribution, the probability that a score falls between -3z and +2z can be calculated as the difference between the cumulative probabilities of +2z and -3z.
Using a standard normal distribution table or calculator, we find that the cumulative probability of +2z is approximately 0.9772, and the cumulative probability of -3z is approximately 0.0013.
Therefore, the probability that a score falls between -3z and +2z is:
0.9772 - 0.0013 = 0.9759
Converting to a percentage, we get:
0.9759 x 100% ≈ 97.59%
So the probability that a score falls between -3z and +2z is approximately 97.59%.
To know more about Probability:
https://brainly.com/question/11234923
#SPJ4
Which of the following statements is true about the sum of a rational and an irrational number?
A.
The sum of a rational and irrational number is always an irrational number.
B.
The sum of a rational and irrational number is always a rational number.
C.
The sum of a rational and irrational number is never an irrational number.
D.
The sum of a rational and irrational number is sometimes a rational number.
Answers
It is incorrect to say that the sum of a rational and an irrational number is always irrational (A) or always rational (B). Similarly, it is incorrect to say that the sum is never irrational (C). The correct statement is that the sum of a rational and irrational number is sometimes a rational number (D).
The correct answer is D. The sum of a rational and irrational number is sometimes a rational number.
To understand why, let's consider an example. Let's say we have a rational number, such as 2/3, and an irrational number, such as √2.
When we add these two numbers together: 2/3 + √2
The result is a sum that can be rational or irrational depending on the specific numbers involved. In this case, the sum is approximately 2.94, which is an irrational number. However, if we were to choose a different irrational number, the result could be rational.
For instance, if we had chosen π (pi) as the irrational number, the sum would be:2/3 + π
In this case, the sum is an irrational number, as π is irrational. However, it's important to note that there are cases where the sum of a rational and an irrational number can indeed be rational, such as 2/3 + √4, which equals 2.
for more search question sum
https://brainly.com/question/30442577
#SPJ8
If the sixth term of a sequence is 128 and the common ratio is 2, then what is the first term? 1, 2 or ,4
Answers
the Answer C: 4
Step-by-step explanation:
convert 3 4/5 into a improper fraction with steps please
Answers
Answer:
Step-by-step explanation:
((3×5)+4)/5=
19/5
The improper fraction is 19/5.
We have to convert \(3 \dfrac{4}{5}\) it into an improper fraction.
To convert into an improper fraction calculation must be done in a single unit following all the steps given below.
Step1; Write the fraction into simple fractions,\(= \dfrac{3 \times 5 + 4}{5}\)
Step2; Solve the following equation.\(=\dfrac{15+4}{5}\\\\=\dfrac{19}{5}\)
Hence, The improper fraction is 19/5.
To know more about Fractions click the link given below.
https://brainly.com/question/21449807
Which shows a correct way to determine the volume of the right rectangular prism?
71cm
8cm
9+1+8 = 18 cm
219 + 1 + 8) = 36 cm
9(3) + 1 = 28 cm
98)(1) = 72 cm

Answers
find the equation of the line tangent to r=1 2cosθ at θ=pi/2
Answers
To find the equation of the tangent line to the polar curve r = 12cos(θ) at θ = π/2, we need to determine the slope of the tangent line and the point of tangency.
The equation of the line tangent to the polar curve r = 12cos(θ) at θ = π/2 is x = 0.
The slope of the tangent line. The slope of a polar curve at a given point can be found using the derivative formula:
dy/dx = (dy/dθ) / (dx/dθ)
In polar coordinates, the relationship between x and y is given by:
x = rcos(θ)
y = rsin(θ)
Differentiating both x and y with respect to θ,
dx/dθ = dr/dθcos(θ) - rsin(θ)
dy/dθ = dr/dθsin(θ) + rcos(θ)
Substituting r = 12cos(θ), we have:
dx/dθ = d(12cos(θ))/dθ×cos(θ) - 12cos(θ)sin(θ)
dy/dθ = d(12cos(θ))/dθsin(θ) + 12cos(θ)×cos(θ)
Simplifying these derivatives, we find:
dx/dθ = -12cos(θ)×sin(θ) - 12cos(θ)×sin(θ) = -24cos(θ)×sin(θ)
dy/dθ = 12cos(θ)×sin(θ) - 12sin²2(θ) + 12cos²2(θ) = 12cos(θ)
Now, let's substitute θ = π/2 into the derivatives:
dx/dθ = -24cos(π/2)sin(π/2) = -240×1 = 0
dy/dθ = 12cos(π/2) = 0
At θ = π/2, the derivatives dx/dθ and dy/dθ both evaluate to 0. This indicates that the curve is not changing with respect to θ at this point, implying that the tangent line is vertical.
The polar equation r = 12cos(θ) represents a circle with a radius of 12 centred at the origin. At θ = π/2, the point of tangency is on the circle with coordinates (0, 12).
Since the tangent line is vertical and passes through the point (0, 12), its equation can be written as x = 0.
To know more about equation here
https://brainly.com/question/29657992
#SPJ4
50 POINTS!
Which distance measures 5 units?
A number line going from negative 8 to positive 8. A closed circle appears at negative 8 and is labeled W. A closed circle appears at negative 3 and is labeled X. A closed circle appears at positive 1 and is labeled Y. A closed circle appears at positive 5 and is labeled Z. An orange arrow line extends the length of the number line and contains all points.
A. the distance between points W and X
B. the distance between points X and Y
C. the distance between points X and Z
D. the distance between points Y and Z
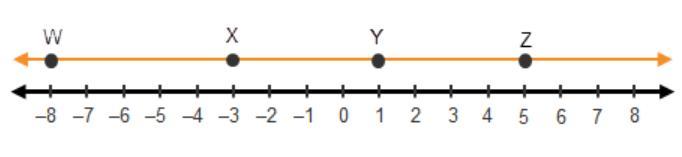
Answers
Answer:
A. the distance between points W and XStep-by-step explanation:
Looking for the distance of 5 units
A. the distance between points W and X
-3 - (-8) = -3 + 8 = 5CorrectB. the distance between points X and Y
1 - (-3) = 1 + 3 = 4 < 5IncorrectC. the distance between points X and Z
5 - (-3) = 5 + 3 = 8 > 5IncorrectD. the distance between points Y and Z
5 - 1 = 4 < 5IncorrectWhich expression is equivalent to −2(3x + 5y)?
−6x − 10y
−6x + 5y
5y(3x − 2)
3x(−2 + 5y)
Answers
this expression means everything inside the bracket (3x+5y) is to be multiplied by -2.
-2 x 3x = -6x
-2 x 5y= -10y
-6x-10y
Let S T be sets. Prove that S CT, if and only if, 25 C 2T. 9.10. Let S, T be sets. Prove that 23 n 21 = 2SNT.
Answers
First, let's prove that if S ⊂ T, then S ∩ T = S. Since S is a subset of T, all elements of S are also elements of T. Therefore when finding the intersection of S and T, we will only get elements that are in both sets, which are all the elements of S. So, S ∩ T = S.
Next, let's prove the converse, that if S ∩ T = S, then S ⊂ T. If S ∩ T = S, then all elements of S are in the intersection of S and T, meaning they are also in T. So, every element of S is also an element of T, which means S is a subset of T (S ⊂ T).
In response to the given question, the statement to be proved is S ⊆ CT if and only if 25 ⊆ 2T. It is also required to prove that 2³ ∩ 2¹ = 2S∩T. To prove the given statement, it is necessary to prove that S is a subset of CT if and only if 25 is a subset of 2T.
Let us consider the following cases:1) If S is a subset of CT, then for any element s of S, s is also present in CT. Therefore, s must be present in both C and T.2) If 25 is a subset of 2T, then any element x of 25 must be of the form 2t for some t in T.
Therefore, x must also belong to T, since 2 is not an element of T. Since 25 is a subset of 2T, any element of 25 must be of the form 2t for some t in T. Hence 25 ⊆ T.
The statement to be proved is 23 ∩ 21 = 2S∩T. The intersection of two sets, A and B, is defined as the set containing all elements that are common to both sets.
Using this definition, we can write:2³ ∩ 2¹ = {8, 2} Therefore, 2S∩T = {x | x ∈ S and x ∈ T}. Combining these two, we have:2³ ∩ 2¹ = 2S∩T = {8, 2}This proves that 23 ∩ 21 = 2S∩T. Therefore, the required statement has been proved.
learn more about sets here: brainly.com/question/24627919
#SPJ11