Solve for v.
-8 = v + 4
Answers
Answer:
v=-12
Step-by-step explanation:
-8=v+4
-4 -4
-12=v
Answer:
v = -12
Step-by-step explanation:
We have the equation v + 4 = -8
Subtract 4 from both sides.
v + 4 - 4 = -8 - 4
+4 and -4 cancel one another out.
We get v = -12.
I would appreciate brainliest but if not that's ok!
Related Questions
Find inverse function of ƒ:
ƒ(x) = x2 - 7 x ≥ 0
Verify:
ƒ(ƒ-1(x)) = x
ƒ(ƒ-1(x) = (√X+7)2 -7
ƒ(ƒ-1(x) = x
Complete problem in same manner as was completed in the prior problem.
Verify:
ƒ-1(ƒ(x)) = x
Answers
ƒ^(-1)(ƒ(x)) ≠ x. In conclusion, we have found the inverse function of ƒ(x) = x^2 - 7 for x ≥ 0 to be ƒ^(-1)(x) = √(x + 7). However, it does not satisfy the property of ƒ^(-1)(ƒ(x)) = x for all values of x
To find the inverse function of ƒ(x) = x^2 - 7 for x ≥ 0, we can follow these steps:
Step 1: Replace ƒ(x) with y:
y = x^2 - 7
Step 2: Swap x and y:
x = y^2 - 7
Step 3: Solve for y:
x + 7 = y^2
√(x + 7) = y
Step 4: Replace y with ƒ^(-1)(x):
ƒ^(-1)(x) = √(x + 7)
Now, let's verify the inverse function:
To verify ƒ(ƒ^(-1)(x)) = x:
ƒ(ƒ^(-1)(x)) = (√(x + 7))^2 - 7
ƒ(ƒ^(-1)(x)) = (x + 7) - 7
ƒ(ƒ^(-1)(x)) = x
Therefore, we have verified that ƒ(ƒ^(-1)(x)) = x.
Now, let's verify ƒ^(-1)(ƒ(x)) = x:
ƒ^(-1)(ƒ(x)) = ƒ^(-1)(x^2 - 7)
ƒ^(-1)(ƒ(x)) = √(x^2 - 7 + 7)
ƒ^(-1)(ƒ(x)) = √x^2
ƒ^(-1)(ƒ(x)) = |x|
The result is the absolute value of x, which is not equal to x for all values of x.
Therefore, ƒ^(-1)(ƒ(x)) ≠ x.
In conclusion, we have found the inverse function of ƒ(x) = x^2 - 7 for x ≥ 0 to be ƒ^(-1)(x) = √(x + 7). However, it does not satisfy the property of ƒ^(-1)(ƒ(x)) = x for all values of x.
Learn more about inverse function here:
https://brainly.com/question/29141206
#SPJ11
Solve for
0.5(r +2.75) = 3
Please I really need help I’m stuck
Answers
Answer:
r=3.25
Step-by-step explanation:
3 divided by 0.5=6
6-2.75=3.25
r=3.25
Answer:
r = 3.25
Step-by-step explanation:
Isolate the variable, r. Note the equal sign, what you do to one side, you do to the other.
Do the opposite of PEMDAS. PEMDAS is the order of operations, and stands for:
Parenthesis
Exponents (& roots)
Multiplications
Divisions
Additions
Subtractions
~
First, divide 0.5 from both sides of the equation:
(0.5(r + 2.75))/0.5 = (3)/0.5
r + 2.75 = 3/0.5
r + 2.75 = 6
Next, subtract 2.75 from both sides of the equations:
r + 2.75 (-2.75) = 6 (-2.75)
r = 6 - 2.75
r = 3.25
r = 3.25 is your answer.
~
Edward works as a waiter, where his monthly tip income is normally distributed with a mean of $2,000 and a standard deviation of $350. Use this information to answer the following questions. Record yo
Answers
The probability that Edward’s monthly tip income exceeds $2,350 is 0.8413.
Given that Edward works as a waiter, where his monthly tip income is normally distributed with a mean of $2,000 and a standard deviation of $350.
The z score formula is given by;`z = (x - μ) / σ`
Where; x is the raw scoreμ the mean of the populationσ is the standard deviation of the population.
The probability that Edward’s monthly tip income exceeds $2,350 is to be found.`z = (x - μ) / σ``z = (2350 - 2000) / 350``z = 1`
The value of z is 1.
To find the area in the right tail, use the standard normal distribution table.
The table value for z = 1.0 is 0.8413.
Therefore, the probability that Edward’s monthly tip income exceeds $2,350 is 0.8413.
Know more about probability here:
https://brainly.com/question/251701
#SPJ11
For a large random sample, what z-score(s) cover the "middle 98%" of the normal curve and represent the 98% confidence level (CL)?
Answers
To determine the z-score(s) that cover the "middle 98%" of the normal curve and represent the 98% confidence level (CL), we can use the properties of the standard normal distribution.
The "middle 98%" refers to the area under the normal curve between the z-scores that enclose the central 98% of the distribution. In a standard normal distribution, the mean is 0 and the standard deviation is 1.
Since the distribution is symmetric, we need to find the z-score(s) that correspond to the area of (1 - 0.98) / 2 = 0.01 on each tail of the distribution. The remaining 0.02 is split equally between the two tails.
To find the z-score(s), we can use a standard normal distribution table or a calculator.
Looking up the value of 0.01 in the z-table, we find that the z-score that corresponds to the lower tail is approximately -2.33. This means that 1% of the area lies to the left of z = -2.33.
To find the z-score for the upper tail, we use the symmetry of the distribution. The z-score that corresponds to the upper tail is the negative of the z-score for the lower tail, so it is approximately 2.33.
Therefore, the z-scores that cover the "middle 98%" of the normal curve and represent the 98% confidence level (CL) are approximately -2.33 and 2.33.
To learn more about symmetry : brainly.com/question/1597409
#SPJ11
probabilaty with words.
I dont understand how I put them in the right catagory what calculation do I use

Answers
Answer:
you dont really need calculations for this exercise, you just need to think a little logic to find the right answer
Step-by-step explanation:
D. impossible
After Wednesday comes Thursday
B. Certain
After summer comes autumn
E. Evens
they're 3 prime numbers from 1 to 6
A. Likely
there are no numbers smaller than 1 on a dice, the only number that could not be bigger than 1 is 1 itself
C. Unlikely
a leap happens once a 4 years so the chance is 1/4
if they are linearly dependent, find scalars that are not all zero such that the equation below is true. If they are linearly independent, find the only scalars that will make the equation below true.(1 point) Are the vectors [-5 4 5] [2 -1 5] [-17 16 45] linearly independent?
Answers
The vectors [-5 4 5], [2 -1 5], and [-17 16 45] are linearly dependent with scalars (1, 3, 1) as an example of a non-zero solution.
To determine if the vectors [-5 4 5], [2 -1 5], and [-17 16 45] are linearly independent, we need to find the scalars a, b, and c that satisfy the equation:
a * [-5 4 5] + b * [2 -1 5] + c * [-17 16 45] = [0 0 0]
If the only solution is a = b = c = 0, the vectors are linearly independent. If there are other solutions where a, b, and c are not all zero, the vectors are linearly dependent.
Let's form a matrix with these vectors as columns:
|-5 2 -17|
| 4 -1 16|
| 5 5 45|
Now, we can row reduce this matrix to its reduced row echelon form (RREF):
| 1 -2 5|
| 0 1 -3|
| 0 0 0|
From the RREF, we can write the system of linear equations:
x - 2y + 5z = 0
y - 3z = 0
Solving this system, we get:
y = 3z
x = 2y - 5z = 6z - 5z = z
Since z can be any scalar, we have infinitely many solutions where not all of a, b, and c are zero. For example, when z = 1, we get x = 1 and y = 3. So, the scalars (1, 3, 1) make the equation true.
Thus, the vectors [-5 4 5], [2 -1 5], and [-17 16 45] are linearly dependent with scalars (1, 3, 1) as an example of a non-zero solution.
To learn more about linearly dependent vectors visit : https://brainly.com/question/30840640
#SPJ11
A car show is making a model of 1980 Ford truck. The model is 10 inches long. If the model truck has a scale of 3 in: 2ft, how tall is the actual truck?
Answers
Answer:
Step-by-step explanation:
3 inches is 2 feet
10 inches is 6.66 feet (no this isn't a joke)
Which of the following is a univariate display of quantitative data? histogram mosaic plot bar chart scatterplot
Answers
A histogram is a univariate display of quantitative data that organizes data into bins and shows the frequency of observations within each bin.
A histogram is a graphical representation that displays the distribution of quantitative data. It consists of a series of contiguous bars, where each bar represents a specific range or bin of values, and the height of the bar corresponds to the frequency or count of observations falling within that range.
Histograms are commonly used to visualize the shape, central tendency, and spread of a dataset. By examining the heights of the bars, one can determine the frequency of values within each bin and identify patterns such as peaks or clusters. This makes histograms an effective tool for exploring the distribution and characteristics of a single variable in a dataset.
Learn more about Dataset here: brainly.com/question/24058780
#SPJ11
A ratio that compares a number to 100 is a(n) ?
percent
estimate
round
approximation
Answers
the answer is an percent
two points in a rectangular coordinate system have the coordinates (4.8, 2.5) and (−3.2, 5.0), where the units are centimeters. determine the distance between these points.
Answers
To determine the distance between two points in a rectangular coordinate system, we can use the distance formula. Given the coordinates of the points (4.8, 2.5) and (-3.2, 5.0), we can calculate the distance as follows:
Distance = √((x2 - x1)^2 + (y2 - y1)^2)
Plugging in the values, we get:
Distance = √((-3.2 - 4.8)^2 + (5.0 - 2.5)^2)
Simplifying further:
Distance = √((-8)^2 + (2.5)^2)
Distance = √(64 + 6.25)
Distance = √70.25
Distance ≈ 8.38 centimeters
Therefore, the distance between the points (4.8, 2.5) and (-3.2, 5.0) is approximately 8.38 centimeters.
Learn more about coordinate system here: brainly.com/question/11004434
#SPJ11
Can someone please help!!!

Answers
because distance between points must be equal
A group of adults plus one child attend a movie at Regal Cinemark. Tickets cost $11 for adults and $7 for children. The total cost for the movie is $72. Write an equation to find the number of adults in the group.
Answers
Answer:
Y=11x+7
Step-by-step explanation:
Which one would be correct

Answers
Answer:
D
Step-by-step explanation:
The graph starts from 55 and stops at 65 and the only answer that is between that range is D.
Hope it helps:-)
a random sample x1,x2 ...,xn of size n is taken from a poisson distribution with a mean of λ, 0 < λ < [infinity]. (a) show that the maximum likelihood estimator for λ is bλ
Answers
To find the maximum likelihood estimator (MLE) for λ, we need to maximize the likelihood function L(λ) with respect to λ of the Poisson distribution
First, let's write the probability density function (PDF) of the Poisson distribution:
P(X = k) = (e^(-λ) * λ^k) / k!
The likelihood function can be defined as the product of the probabilities for each observation in the random sample. Since the sample is independent and identically distributed, we can write the likelihood function as:
L(λ) = P(x1, x2, ..., xn | λ) = P(x1 | λ) * P(x2 | λ) * ... * P(xn | λ)
Taking the logarithm of the likelihood function (log-likelihood) will simplify the calculations. The log-likelihood function is:
log(L(λ)) = log(P(x1 | λ)) + log(P(x2 | λ)) + ... + log(P(xn | λ))
Now, let's calculate the derivative of the log-likelihood function with respect to λ:
d/dλ log(L(λ)) = d/dλ (log(P(x1 | λ)) + log(P(x2 | λ)) + ... + log(P(xn | λ)))
= d/dλ (log(P(x1 | λ))) + d/dλ (log(P(x2 | λ))) + ... + d/dλ (log(P(xn | λ)))
To find the MLE, we set the derivative equal to zero and solve for λ:
d/dλ log(L(λ)) = 0
The derivative of log(P(x | λ)) with respect to λ can be calculated using the logarithmic differentiation technique. After taking the derivative, we equate it to zero and solve for λ.
By solving the equation, we will obtain the MLE for λ.
Learn more about Poisson distribution: https://brainly.com/question/9123296
#SPJ11
I really need help I don't know how to solve this. : (
An object is traveling at a steady speed of 9 9/10 mi/h. How long will it take the object to travel 2 1/10 mi? First round to the nearest integer to find the estimated answer. Then find the exact answer.
Answers
Answer:
12.73 mins
Step-by-step explanation:
velocity: 9.9 mi/h
distance: 2.1 mi
d=vt
t = d/v = 2.1/9.9 = 0.21h
convert to minutes: 2.1/9.9 x 60 = 12.73 min
suppose that s is a nonempty set of real numbers that is bounded. prove that infs~sups.
Answers
It is given that a set of real numbers s is non-empty and bounded. The objective is to prove that inf s ≤ sup s. This statement can be justified as below.
Firstly, as per the definition of bounded set, it is known that the set s has both lower and upper bounds. Thus, the infimum and supremum of s exist and are denoted as inf s and sup s, respectively.
Since s is non-empty and bounded, it can be observed that every element of the set s is greater than or equal to inf s and less than or equal to sup s.
Therefore, inf s is the greatest lower bound of s and sup s is the least upper bound of s, implying that inf s ≤ sup s. Hence, it is proven that inf s ≤ sup s for a non-empty set s of real numbers that is bounded.
To know more about non-empty visit:
https://brainly.com/question/1581607
#SPJ11
Suppose the volume of a rectangular shopping cart basket is 12,090 cubic inches. If the length measures 31 inches and the width measures 19.5 inches, how high is the shopping cart basket?
Answers
Answer:
\(\boxed {\tt h=20\ inches}\)
Step-by-step explanation:
The volume of a rectangular prism can be found using the following formula.
\(v=l*w*h\)
We know that the volume is 12,090 cubic inches, the length is 31 inches, and the width is 19.5 inches.
\(v= 12,090 \ in^3\\l=31 \ in \\ w=19.5 \ in\)
\(12,090 \ in^3= 31 \ in * 19.5 \ in * h\)
Multiply 31 inches and 19.5 inches.
\(12,090 \ in^3= 604.5 \ in^2 * h\)
We are trying to find h, therefore we must isolate it. h is being multiplied by 604.5 square inches. The inverse of multiplication is division. Divide both sides of the equation by 604.5 in²
\(\frac{12,090 \ in^3}{604.5 \ in^2}= \frac{604.5 \ in^2 *h}{604.5 \ in^2}\)
\(\frac{12,090 \ in^3}{604.5 \ in^2}=h\)
\(20 \ in =h\)
The height of the shopping basket is 20 inches.
guys please help this is a math question
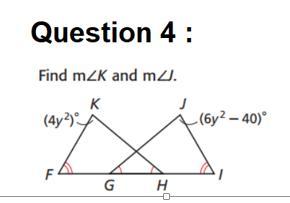
Answers
Answer:
81.5
Step-by-step explanation:
<G and <H are congruent
<F and <I are congruent
so the last two angles in both triangles must also be congruent
this means that <K and <J are congruent
so we can create this equation: <K = <J
substitute the angles with what we know: 4\(y^{2}\) = 6\(y^{2}\) - 40
add 40 to both sides and subtract 4\(y^{2}\) from both sides: 40 = 2\(y^{2}\)
you get: 20 = \(y^{2}\)
root square on both sides: \(\sqrt{20}\) = \(\sqrt{y^{2} }\)
you get: y ≈ 4.5
substitute this into one of the equations for a missing variable:
6\(y^{2}\) -----> 6 (4.5 x 4.5) - 40
6 ( 20.25) - 40
121.5 - 40
81.5
If x=5 and the area of the rectangle is 30 what is the other length of the rectangle?
Answers
Answer:
The other length would be 6.
Step-by-step explanation:
Rectangle area is l times height. So x is either the length for height. So we have 5 times x = 30. To find the other length we have to take 30/5 which equals 6
A car is 150 inches long. A truck is 60% longer than the car.
How long is the truck?
Answers
Answer: Therefore, the truck is 240 inches long.
Step-by-step explanation:
truck = 150 + 60% of 150
= 150 + 60/100 * 150
= 150+90
= 240 inches
Can someone please help me solve for Y and X. Question number 5

Answers
Using the triangle sum theorem, x = 7 and y = 18.
What is the Triangle Sum Theorem?The theorem that says that all the interior angles of a triangle will be equal to 180 degrees is referred to as the triangle sum theorem.
In the diagram given, since vertical angles are congruent, therefore:
(11x - 9) + (6x - 2) + 72 = 180 [triangle sum theorem]
Solve for x
11x - 9 + 6x - 2 + 72 = 180
17x + 61 = 180
17x = 180 - 61
17x = 119
x = 7
Also,
(5y - 8) + (11x - 9) + 30 = 180 [triangle sum theorem]
5y - 8 + 11x - 9 + 30 = 180
5y + 13 + 11x = 180
Plug in the value of x
5y + 13 + 11(7) = 180
5y + 13 + 77 = 180
5y + 90 = 180
5y = 180 - 90
5y = 90
y = 90/5
y = 18
Learn more about triangle sum theorem on:
https://brainly.com/question/7696843
#SPJ1
Find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes, and one vertex in the plane.
Answers
The volume of the largest rectangular box in the first octant with three faces in the coordinate planes, and one vertex in the plane is V = xyz, where x, y, and z are the lengths of the sides of the rectangular box.
To find the largest volume, we need to maximize x, y, and z. Since we have three faces in the coordinate planes, one vertex will be at the origin (0, 0, 0). The other two vertices will lie on the coordinate axes.
Let's assume the vertex on the x-axis is (x, 0, 0), and the vertex on the y-axis is (0, y, 0). The third vertex on the z-axis will be (0, 0, z). Since the box is in the first octant, all the coordinates must be positive.
To maximize the volume, we need to find the maximum values for x, y, and z within the constraints. The maximum values occur when the box touches the coordinate planes. Therefore, the maximum values are x = y = z.
Substituting these values into the volume formula, we get V = xyz = x³. Therefore, the volume of the largest rectangular box is V = x³.
Learn more about constraints here
brainly.com/question/32387329
#SPJ11
What is the maximum volume of a rectangular box situated in the first octant, with three of its faces lying on the coordinate planes, and one of its vertices located in the plane?
consider a sequence of random variables y1,y2,.... where each yi is bernoulli. random variable x equals the value of i such that y i$$ is the first y with value 1. the random variable x is
Answers
The answer to your question is that the random variable x represents the index of the first occurrence of a success domain (i.e., y with value 1) in the sequence of Bernoulli random variables.
let's break down the components of the question. A Bernoulli random variable is a type of discrete probability distribution that represents the outcome of a single binary event (e.g., success or failure). In this case, each yi is a Bernoulli random variable, which means it can take on one of two possible values: 1 (success) or 0 (failure).
The random variable x is defined as the index of the first occurrence of a success in the sequence of yi random variables. For example, if y1 = 0, y2 = 1, y3 = 0, y4 = 0, y5 = 1, then x would equal 2, since y2 is the first yi with a value of 1. To calculate the value of x, we need to examine each yi in the sequence until we find the first success. Once we find the first success, we record the index of that yi as the value of x and stop examining subsequent yis. This means that x can only take on integer values from 1 to infinity (since there may be no successes in the sequence).
To know more about domain visit:
https://brainly.com/question/28135761
#SPJ11
need help please (serious answers only)

Answers
Answer:
66
Step-by-step explanation:
B is 57
C is 57
180 - (57 x 2) =
180 - 114 = 66
Which expression has a positive value? A. (negative 5) (negative 9) B. 2 minus 4 C. 12 divided by (negative 4) D. Negative 3 + (negative 7)
Answers
On friday night, the owner of chez pierre in downtown chicago noted the amount spent for dinner for 28 four-person tables. 110 118 124 185 129 128 122 139 120 95 119 99 191 130 84 110 149 123 76 175 143 83 110 76 165 67 102 151. click here for the excel data file.
(a) Find the mean, median, and mode. (Round your answers to 2 decimal places.) NOTE - (It also asks for the count)
(b) Are the data symmetric or skewed? If skewed, which direction?
multiple choice
a. Symmetric
b. Skewed right
c. Skewed left
Answers
- Mean: 119.43- Median: 118.50- Mode: 110 - Count: 28
To find the mean, we add up all the values and divide by the number of observations. In this case, the sum of the values is 3342, and since there are 28 observations, the mean is 3342/28 = 119.43.
The median is the middle value when the data is arranged in ascending order. In this case, there are 28 observations, so the median is the average of the 14th and 15th values. When the data is ordered, the 14th value is 118 and the 15th value is 124. Therefore, the median is (118 + 124)/2 = 118.50.
The mode is the value that appears most frequently in the dataset. In this case, the value 110 appears three times, which is more than any other value. Hence, the mode is 110.
The count simply refers to the number of observations in the dataset, which is 28 in this case.
(b) The data is skewed right.
When data is symmetric, it means that the values are evenly distributed around the mean, resulting in a bell-shaped curve. In this case, the data is not symmetric. Looking at the dataset, we can observe that there are several smaller values on the left side, while the right side has a few larger values. This indicates a right skew or positive skewness.
Skewness refers to the asymmetry of a distribution. In a right-skewed distribution, the tail of the distribution extends towards the right, indicating a longer right tail. Therefore, the correct answer is b. Skewed right, indicating that the data is positively skewed.
to learn more about Median click here:
brainly.com/question/3515636
#SPJ11
Mr. JB has a rectangular lot that measures 550 meters by 550 km. What is the area of the land in square meter. He i selling the whole lot for 206,250,000 pesos how much is the price per square meter?
Answers
9514 1404 393
Answer:
15/22 peso/m^2 ≈ 0.68182 peso/m^2
Step-by-step explanation:
The area is the product of the dimensions. 1 km = 1000 m.
A = (550 m)(550·1000 m) = 302,500,000 m^2
The price per square meter is ...
206,250,000/302,500,000 peso/m^2
= 15/22 peso/m^2 ≈ 0.68182 peso/m^2
Which statistical measurement informs a CTRS about how well the assessment results compare to what is being measured?A.Equivalent-forms reliabilityB.Criterion-related validityC.Test-retest reliabilityD.Construct validity
Answers
The statistical measurement that informs a CTRS about how well the assessment results compare to what is being measured is Construct validity.
Construct validity assesses how well the assessment measures the intended construct or trait, and compares the results to other tests or measures of the same construct to determine how accurate and reliable the assessment is.
To know more about statistical measurement visit:
https://brainly.com/question/31036349
#SPJ11
Prove that an integer consisting of 3n ones is divisible by 3n (e.g. 111 is divisible by 3, 111,111,111 is divisible by 9, etc.) Prove it by induction. Notice, that while the number with a sum of digits divisible by 3 is itself a multiple of 3 and the number with a sum of digits divisible by 9 is itself a multiple of 9, it is NOT true that the number with a sum of digits divisible by 27 is necessarily a multiple of 27.
Answers
For proof of 3 divisibility, abc is a divisible by 3 if the sum of abc (a + b + c) is a multiple of 3.
Integers divisible by 3The proof for divisibility of 3 implies that an integer is divisible by 3 if the sum of the digits is a multiple of 3.
Proof for the divisibility111 = 1 + 1 + 1 = 3 (the sum is multiple of 3 = 3 x 1) (111/3 = 37)
222 = 2 + 2 + 2 = 6 (the sum is multiple of 3 = 3 x 2) (222/3 = 74)
213 = 2 + 1 + 3 = 6 ( (the sum is multiple of 3 = 3 x 2) (213/3 = 71)
27 = 2 + 7 = 9 (the sum is multiple of 3 = 3 x 3) (27/3 = 9)
Thus, abc is a divisible by 3 if the sum of abc (a + b + c) is a multiple of 3.
Learn more about divisibility here: https://brainly.com/question/9462805
#SPJ1
Drew painted his uncle's barn on saturday. it took him 7 hours to paint the whole barn, and his uncle paid him 133 dollars for his work. what was drew's pay rate, in dollars per hour?
Answers
The total amount paid in dollars per hour is $19.
Unitary Method:
The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value.
It is given that the total amount given by the uncle is $133 for the work done by Barn for 7 hours.
We have to find the amount paid per hour.
Total amount given = $133
Number of hour Barn work = 7 hours
Amount paid per hour = 133/ 7
= $ 19
Therefore the amount paid per hour is $19.
To know more about the unitary method refer to the link given below:
https://brainly.com/question/24587372
#SPJ4