Answers
Answer:
Step-by-step explanation:
\(\frac{x-4}{3}\) ≥ - 2
x - 4 ≥ - 6
x ≥ - 2
x ∈ [ - 2 , ∞ )
2 - 6x < 32
- 6x < 30
x > - 5
x ∈ ( - 5 , ∞ )

Related Questions
On weekends, Ben mops the kitchen floor. Below is an image that showsthe dimensions of the floor, in feet.10484Question: What is the the total area of the kitchen floor?

Answers
The given figure is :
According to the given figure
Area of ABCDEF = Area of rectangle ABCDG and Area of square GDEF
In rectangle ABCG
Length = 10, Width = 4 unit
Area of recatngle ABCG = 10 x 4
Area of rectangle = 40 unit²
In the square GDEF
Side length = 4 unit
Area of GDEF =4 x 4
Area of GDEF = 16 unit²
Area of the figure = 40 + 16
Area of the figure = 56 unit²
Answer : 56unit²

Please help ASAP!!!!

Answers
Answer:
2/25
Step-by-step explanation:^2 = 1/25
Cubic Root 8 = cubic root = 2^3 = 2
(1/25)*(2) = 2/25
What kind of sequence?
8, 4, 1, -1, ...
A: Geometric
B: Arithmetic
C: Neither
Answers
Answer:
C. Neither
Step-by-step explanation:
6) A bag contains 4 red marbles, 3 green, 5 blue. Someone offers you a game : If you pick red marble you win $4, if blue loose $2, green loose $1. What is the expected value of the game
Answers
Answer:
11
Step-by-step explanation:
i just need 11 more than ill be fine
dont know the answer pls help :(

Answers
Answer:
x=3
Step-by-step explanation:
7x-3=18
7x=18+3
7x=21
x=3
please help for brainliest and a lot of points

Answers
Answer:The solution is in the attached file
Step-by-step explanation:

Need help quickly!
Given negative four and one-sixth times negative three and fifteen hundredths, determine the product.
negative thirteen and one eighth
thirteen and one eighth
twelve and 1 over 40
twelve and 6 over 15
Answers
The product of the numbers is B. thirteen and one eighth.
How to calculate the product?From the information, we are negative four and one-sixth times negative three and fifteen hundredths.
The product will be:
= (-4 1/6) × (-3 15/)
= - 4 1/6 × 3 3/20
= - 25/6 × -63/20
= 13 1/8
The correct option is thirteen and one eighth.
Learn more about product on:
brainly.com/question/10873737
#SPJ1
Dog A has 10 and Dog B has 2. How many more bones does Dog A have than
Answers
Answer: 8 more dogs.
Step-by-step explanation:
All you have to do is subtract 10 by 2 and you’ll get your answer.
Answer:
2
Step-by-step explanation:
Consider the following sample of observations on coating thickness for low-viscosity paint:
.83 .88 .88 1.04 1.09 1.12 1.29 1.31 1.48 1.49 1.59 1.62 1.65 1.71 1.76 1.83
Assume that the distribution of coating thickness is normal (a normal probability plot strongly supports this assumption).
a. Calculate a point estimate of the mean value of coating thickness, and state which estimator you used.
b. Calculate a point estimate of the median of the coating thickness distribution, and state which estimator you used. c. Calculate a point estimate of the value that separates the largest 10% of all values in the thickness distribution from the remaining 90%, and state which estimator you used. [Hint: Express what you are trying to estimate in terms of m and s.]
d. Estimate P(X < 1.5), i.e., the proportion of all thickness values less than 1.5. [Hint: If you knew the values of m and s, you could calculate this probability. These values are not available, but they can be estimated.]
e. What is the estimated standard error of the estimator that you used in part (b)?
Answers
The coating thickness distribution is normal and has a mean value of 1.245.
What is mean?In statistics, in addition to the mode and median, the mean is one of the measures of central tendency. Simply put, the mean is the average of the values in the given set. It indicates that values in a particular data set are distributed equally. The three most frequently employed measures of central tendency are the mean, median, and mode.
To calculate the data's coating thickness, sample mean is employed.
The following formula is used to determine the mean value's point estimate:
\(\bar x = \frac{1}{n} \sum x_i\)
The typical probability plot shown there has a rather straight pattern. Assume right now that the coating thickness distribution is normal and has a mean value:
\(\bar x = \frac{19.92}{16}\\\\\bar x = 1.245\)
Learn more about mean here:
https://brainly.com/question/28670966
#SPJ4
Question 1
The value of a new technological equipment depreciates (decreases) after it is purchased. Suppose that the value of the technological equipment depreciates according to an exponential decay model. Suppose that the value of the equipment is $20000 at the end of 6 years, and its value has been decreasing at the rate of 10% per year. Find the value of the technological equipment when it was new.
Answers
The value of the technological equipment when it was new according to an exponential decay model is approximately $37,633.52.
It is given to us that the value of a new technological equipment depreciates (decreases) after it is purchased, the value of the technological equipment depreciates according to an exponential decay model.
We know that the value of the equipment is $20000 at the end of 6 years, and its value has been decreasing at the rate of 10% per year.
Let the purchase price of machine be $P
Rate of depreciation = 10% p.a.
Period years.
∴ Present value = $20,000
Depreciated value can be calculated by t(6) ---> [∵ Depriciated value = A]
⇒ $20,000 = P(1−10/100)⁶
⇒ $20,000 = P(9/10)⁶
⇒ P = $20,000 (9/10)⁶ A = P(1-100)t
⇒ P = $20,000 × 10/9 × 10/9 × 10/9 × 10/9 × 10/9 × 10/9
⇒ P = $37,633.528463178 ≈ 37,633.52
The value of the technological equipment when it was new was approximately $37,633.52.
To learn more about exponential decay model, click here:
brainly.com/question/28596571
#SPJ4
Estimate the integral ∫ sin /(t) using a Taylor polynomial for sin t about t = 0 of degree 5.
Answers
To estimate the integral ∫ sin(t)/t using a Taylor polynomial for sin t about t = 0 of degree 5, we can first write out the Taylor series for sin t:
sin t = t - (t^3)/3! + (t^5)/5! - (t^7)/7! + ...
If we truncate this series at the fifth degree, we get:
sin t ≈ t - (t^3)/3! + (t^5)/5!
Now, we can substitute this approximation into the integral:
∫ sin(t)/t dt ≈ ∫ (t - (t^3)/3! + (t^5)/5!)/t dt
= ∫ (1 - (t^2)/3! + (t^4)/5!)/dt
= t - (t^3)/(3*3!) + (t^5)/(5*5!) + C
where C is the constant of integration. We can evaluate this expression between limits, say from 0 to 1, to get an estimate for the integral:
∫ sin(t)/t dt ≈ 1 - (1^3)/(3*3!) + (1^5)/(5*5!) - (0^3)/(3*3!) + (0^5)/(5*5!) + C
= 0.946
So, the estimate for the integral ∫ sin(t)/t using a Taylor polynomial for sin t about t = 0 of degree 5 is approximately 0.946.
To estimate the integral ∫sin(t) using a Taylor polynomial for sin(t) about t=0 of degree 5, we first need to write the Taylor polynomial of sin(t). The Taylor polynomial of degree 5 for sin(t) about t=0 is:
P_5(t) = t - (t^3)/6 + (t^5)/120
Now, to estimate the integral, we integrate P_5(t) with respect to t:
∫sin(t) ≈ ∫(t - (t^3)/6 + (t^5)/120) dt
The integral of this polynomial is:
∫P_5(t) dt = (t^2)/2 - (t^4)/24 + (t^6)/720 + C
Here, C is the constant of integration.
Learn more about polynomial here: brainly.com/question/11536910
#SPJ11
A chef is going to use a mixture of two brands of Italian dressing. The first brand contains 8% vinegar, and the second brand contains 11% vinegar. The chef wants to make 360 milliliters of a dressing that is 9% vinegar. How much of each brand should she use?
Answers
To make a 360mL mixture that contains 9% vinegar, use 240mL of the first brand and 120mL of the second brand.
What is an equation?
An equation is a mathematical statement that proves two mathematical expressions are equal in algebra, and this is how it is most commonly used. In the equation 3x + 5 = 14, for instance, the two expressions 3x + 5 and 14 are separated.
You want to set up an equation that will match the word problem. Let's call the amount of the first brand, F, and the amount of the second brand, S.
We want the total mixture to be 360mL so: F + S = 360
Also, you want the total mixture to contain 9% vinegar so:
.08F + .11S = .09(360)
Now, we can solve the system of equations using substitution.
F + S = 360
.08F + .11S = .09(360)
F = 360 - S [solve 1st equation for F]
.08(360 - S) + .11S = .09(360) [substitute into 2nd equation]
28.8 -.08S +.11S = 32.4
.03S = 3.6
S = 120
F + 120 = 360 [substitute answer for S back into original equation]
F = 240
Answer: To make a 360mL mixture that contains 9% vinegar, use 240mL of the first brand and 120mL of the second brand.
To learn more about the equation from the given link
https://brainly.com/question/28218072
#SPJ1
Need help on this explain if you can if you can’t it’s okay!

Answers
Answer:
25 ft
Step-by-step explanation:
based on the graph on the width of the porch with the greatest area is 25
I need help please and thank you ( show your work please)
This table shows a linear relationship.

Answers
Answer:
2x+5
Step-by-step explanation:
if you look at the x and the y coordinates, you'll see that if you multiply the 'x' coordinate by 2 and then add 5, you get the y coordinate
The perimeter of a fence must be no larger than 500 feet in length. The longer side of the fence must be 10 feet more than twice the length of the shorter side. Write and solve and inequality to determine the maximum length of the shorter side of the fence.
Answers
Answer:
The shortest side of the fence can have a maximum length of 80 feet
Step-by-step explanation:
Inequalities
To solve the problem, we use the following variables:
x=length of the longer side
y=length of the sorter side
The perimeter of a rectangle is calculated as:
P = 2x + 2y
The perimeter of the fence must be no larger than 500 feet. This condition can be written as:
\(2x + 2y \le 500\)
The second condition states the longer side of the fence must be 10 feet more than twice the length of the shorter side.
This can be expressed as:
x = 10 + 2y
Substituting into the inequality:
\(2(10 + 2y) + 2y \le 500\)
This is the inequality needed to determine the maximum length of the shorter side of the fence.
Operating:
\(20 + 4y + 2y \le 500\)
Simplifying:
\(20 + 6y \le 500\)
Subtracting 20:
\(6y \le 500 - 20\)
\(6y \le 480\)
Solving:
\(y \le 480 / 6\)
\(y \le 80\)
The shortest side of the fence can have a maximum length of 80 feet
it will locate in beijing, china, is 0.4, and the proba- bility that it will locate in either shanghai or beijing or both is 0.8. what is the probability that the industry will locate (a) in both cities? (b) in neither city?
Answers
Answer:
The probability that the industry will locate in both cities is 0.4. The probability that it will locate in either Shanghai or Beijing or both is 0.8.
Step-by-step explanation:
The probability that the industry will locate in both cities is 0.41. The probability that it will locate in either Shanghai or Beijing or both is 0.81. We can use the formula P(A and B) = P(A) * P(B|A) to calculate the probability of an event occurring in both cities. Let A be the event that the industry locates in Beijing and B be the event that it locates in Shanghai. Then, P(A or B) = P(A) + P(B) - P(A and B) = 0.8. Therefore, P(A and B) = P(A) * P(B|A) = (0.4 * 0.4)/0.8 = 0.2. The probability that the industry will not locate in either city is given by P(neither A nor B) = 1 - (P(A) + P(B) - P(A and B)) = 1 - (0.4 + 0.4 - 0.2) = 0.2.
yw;)
What is the slope of this line?
Enter your answer as a whole number or a fraction in simplest form in the box.

Answers
Answer:
1/4
Step-by-step explanation:
use 2 points from the graph (-4,5) and (0,6) and put them in the distance equation.
(y2-y1)
----------
(x2-x1)
6-5
-------
0-(-4)
1/4
-2.5(e + 17.4) = -50
Answers
To solve the equation -2.5(e + 17.4) = -50, we can use algebraic techniques to isolate the variable e on one side of the equation.
First, we can simplify the left-hand side of the equation by distributing the -2.5 to the expression inside the parentheses:
-2.5e - 2.5(17.4) = -50
Next, we can simplify the expression on the left-hand side by multiplying:
-2.5e - 43.5 = -50
To isolate the variable e, we can add 43.5 to both sides of the equation:
-2.5e = -6.5
Finally, we can solve for e by dividing both sides of the equation by -2.5:
e = 2.6
Therefore, the solution to the equation -2.5(e + 17.4) = -50 is e = 2.6.
A consumer watchdog organization estimates the mean weight of 1-ounce "Fun-Size"
candy bars to see if customers are getting full value for their money. A random sample
of 25 bars is selected and weighted, and the organization reports that a 95% confidence
interval for the true mean weight of the candy bars is 0.982 to 0.988 ounces.
a) What is the point estimate (=sample mean) from this sample?
b) What is the margin of error?
(Hint: find the distance between the sample mean and the upper limit).
c) Interpret the confidence level of 90% in the context of the problem?
Answers
Point estimate from the sample is 0.985, margin error is 0.003.
What is Confidence Interval?Confidence interval is defined as the interval which is the estimate for the parameter of the sample or population to be contained.
(a) To calculate point estimate or sample mean :
Point estimate is the mid point of the confidence interval.
Given that true mean weight of candy bars is 0.982 ounces to 0.988 ounces.
Point estimate = (0.982 + 0.988) / 2 = 1.97 / 2 = 0.985
(b) Margin error is the one half of the total width of the interval.
Margin error = (0.988 - 0.982) / 2 = 0.003
(c) The confidence level of 90% in this problem can be interpreted as , if we do the interval construction for many times, about 90% of the total constructed intervals has the true population mean of weight of fun size candy bars.
Hence the point estimate and margin error are 0.985 and 0.003 respectively.
Learn more about Confidence Interval here :
https://brainly.com/question/18914334
#SPJ1
Write 1= 2x2 + 5x In standard form.
What is the value of b^2 - 4ac?
Answers
Answer:
2x^2+5x-1=0
ax^-bx+c=0
b^2-4ac = 5^2-4(2)(-1) =33
In a class of 80 students, 50 students know english, 55 know french and 46 know german language. 37 students know english and french, 28 students know french and german, 25 students know english and german and 7 students know none of the languages. find out (a) how many students know all the 3 languages?
Answers
The number of students who knows all the 3 languages is 12
Total number of students = 80
Number of students who knows English = 50
Number of students who knows French = 55
Number of students who knows German = 46
Number of students who knows English and French = 37
Number of students who knows French and German = 28
Number of students who knows English and German = 25
Number of students who knows none of the languages = 7
Here we have to use the equation of the union of set
n(E∪F∪G) = n(E) + n(F) + n(G) - n(E∪F) - n(F∪G) - n(E∪G) + n(E∩F∩G)
80 - 7 = 50 + 55 +46 - 37 - 28 -25 + n(E∩F∩G)
n(E∩F∩G) = 73 - 50 -55 -46 +37 +28 +25
n(E∩F∩G) = 12
Hence, the number of students who knows all the 3 languages is 12
Learn more about union here
brainly.com/question/11427505
#SPJ4
Please solve for y P=2x+2y+4
Answers
Answer:
Step-by-step explanation:
P=2x+2y+4
y=p/2-x-2
The equation can represent as y = P/2 - x - 2 after solving for y if the equation is P = 2x + 2y + 4.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
It is given that:
Solve for y P=2x+2y+4
From the data given in the question:
The linear equation is:
P=2x+2y+4
To solve for make the subject as y:
2y = P - 2x - 4
y = (1/2)[P - 2x - 4]
Or
y = P/2 - x - 2
Thus, the equation can represent as y = P/2 - x - 2 after solving for y if the equation is P = 2x + 2y + 4.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ2
7. What is the slope of the line
Problem Set #4
2-y=8x ?
Answers
Answer:
To find the slope of the line, you can use the formula for slope: slope = (y2 - y1)/(x2 - x1). In this case, you can rewrite the equation 2-y = 8x as y = 2 - 8x. This is the standard form of a line: y = mx + b, where m is the slope and b is the y-intercept (the point where the line crosses the y-axis).
Since the equation of the line is already in standard form, you can find the slope by looking at the coefficient of the x term. In this case, the coefficient of the x term is -8, so the slope of the line is -8.
Alternatively, you can plug in the coordinates of two points on the line into the formula for slope to find the slope. For example, if you know that the line passes through the points (1, -14) and (2, -10), you can use these points to find the slope:
slope = (y2 - y1)/(x2 - x1) = (-10 - (-14))/(2 - 1) = (-10 + 14)/1 = 4/1 = 4
This method gives the same result as using the standard form of the equation.
Step-by-step explanation:
GUYS GUYS GUYS!!!!!!! ...Help me please. TwT (pt. 2)


Answers
The value of \(125x^3 + 27y^6z^9\) factors to \((5x + 3y^2z^3)(25x^2 - 15xy^2z^3 + 9y^4z^6).\) and option D is the correct answer.
What is factoring and expanding?In algebra, there are two opposing operations: factoring and expanding. In order to create a longer and more complex expression, expanding entails multiplying out expressions. On the other hand, factoring entails dissecting a complicated expression into smaller factors.
In conclusion, factoring entails division whereas expanding involves multiplication.
To factor \(125x^3 + 27y^6z^9\), we can use the sum of cubes formula:
\(a^3 + b^3 = (a + b)(a^2 - ab + b^2)\)
In this case, a = 5x and \(b = 3y^2z^3\):
Simplify the expression by using the identity and rearranging the expression to get the desired output:
\(125x^3 + 27y^6z^9 = (5x)^3 + (3y^2z^3)^3\\= (5x + 3y^2z^3)((5x)^2 - (5x)(3y^2z^3) + (3y^2z^3)^2)\\= (5x + 3y^2z^3)(25x^2 - 15xy^2z^3 + 9y^4z^6)\)
Therefore, \(125x^3 + 27y^6z^9\) factors to \((5x + 3y^2z^3)(25x^2 - 15xy^2z^3 + 9y^4z^6).\) Hence, option D is the correct answer.
2. The difference of cubes is given by the equation
8x¹⁵ - 125y³
The expression can be written as:
(2x⁵)³ - (5y)³
Learn more about factors here:
https://brainly.com/question/26923098
#SPJ1
in a survey conducted on an srs of 200 american adults, 72% of them said they believed in aliens. give a 95% confidence interval for percent of american adults who believe in aliens.
Answers
American adults believes in alien for the given 95% confidence interval and sample surveyed is in the interval range of ( 0.66 , 0.78 ).
As given in the question,
Sample of American adults surveyed 'n' = 200
Percent of people believes in aliens are success 'p'= 72%
= 0.72
Percent of people who don't believes (failure) in aliens ' 1 - p' = 1 - 0.72
= 0.28
95% Confidence interval that represents Americans adults who believes in aliens
value of z - score for 95% confidence interval = ± 1.96
Margin of error 'MOE'= (z-score)√p ( 1- p) /n
= ( 1.96)√(0.72 × ( 1 - 0.72 )/ 200
= 1.96 ( √0.2016 / 200)
= 1.96 ×√0.001008
= 0.063
Lower limit = p - MOE
= 0.72 - 0.063
= 0.66
Upper limit = p + Margin of error
= 0.72 + 0.063
= 0.78
Therefore, 95% confidence interval with sample size of the Americans adults who believes in alien are in the interval of ( 0.66 , 0.78 ).
Learn more about sample here
brainly.com/question/11045407
#SPJ4
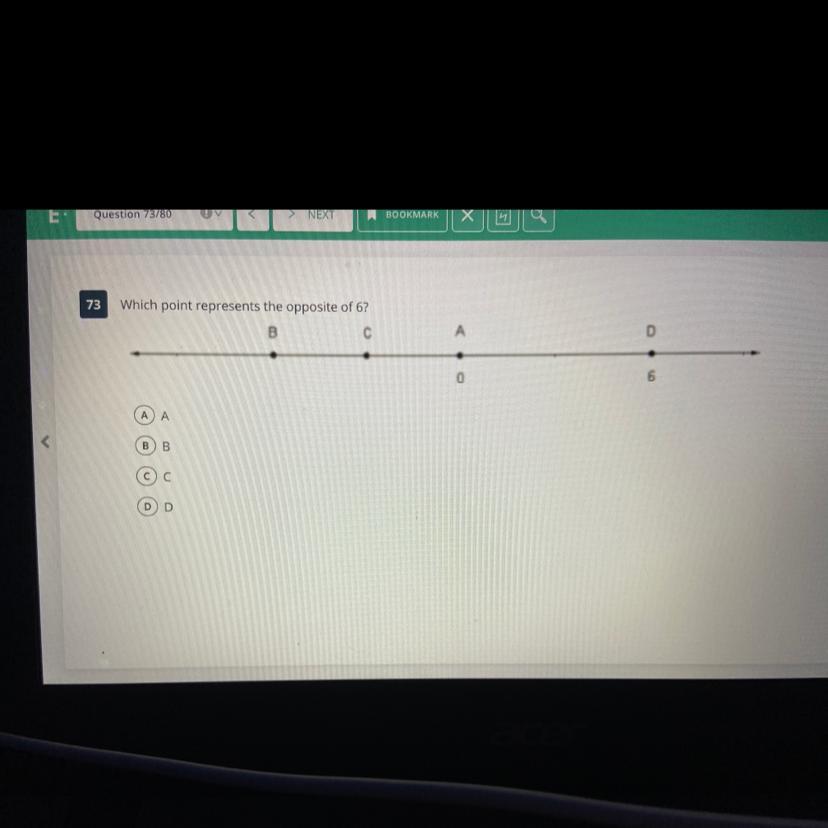
Which Point represents the opposite of six,??
Answers
A. y= 1/2x-14
B. y=1/2x-5
C. y=2x-14
D. y=2x-5

Answers
Answer:
B. y=1/2x-5
Step-by-step explanation:
From the graph, we read the slope of line JK.
slope = rise/run = -3/-6 = 1/2
The equation we need has the same slope.
y = mx + b
y = (1/2)x + b
It passes through point P(6, -2). Now we find b.
-2 = (1/2)(6) + b
-2 = 3 + b
b = -5
The equation is
y = (1/2)x - 5
Due to unexpected circumstances, you take out a loan for $5,000 to pay for a lawyer. You agree to pay it back over the next 5 years at a rate of 22.5% (because your credit score is really really low). At the end of the 5 years, how much did this "unexpected circumstance" end up costing you in all?
Answers
R=22.5
T=5yrs
I=PxRxT= 5000x22.5x5=50x22.5=1125x5=5625
———= ———————
100 =. 100
The answer is $5625
Evaluate the expression when z=7 3z+8
Answers
Answer:
Hi! The answer to your question is \(29\)
Step-by-step explanation:
\(3(7)+8\)
\(3(7) = 21\)
\(21 + 8\)
\(= 29\)
☆*: .。.。.:*☆☆.*: .。..。.:*☆☆*: .。.。.:*☆☆.*: .。..。.:*☆
☁Brainliest is greatly appreciated!☁
Hope this helps!!
- Brooklynn Deka
a rectangle is drawn so the width is 49 inches longer than the height. if the rectangle's diagonal measurement is 61 inches, find the height.
Answers
Refer to the attachment for figure:
The height of the rectangle = 11 inches
What is rectangle?
A rectangle is a type of quadrilateral with parallel sides equal to each other and four equal 90-degree vertices. Because of this, it is also known as an equiangular quadrilateral. Because the opposite sides of a rectangle are equal and parallel, it can also be referred to as a parallelogram.
Let x= height
Width becomes x+49
Diagonal BD=61 inches
By pythagoras theorem,
BD²=BC²+CD²
61²= (x+49)²+x²
3721=x²+98x+2401+x²
On simplification,
x²+49x-660=0
Find the factors
(x+60)(x-11)=0
x=-60, x=11
Consider positive value for height
height = 11 inches
To learn more about the rectangle from the given link
https://brainly.com/question/25292087
#SPJ4

