Solve this equation. Enter your answer in the box. 75 â€"" 3. 5y â€"" 4y = 4y 6.
Answers
Answer:
Solve this equation. Enter your answer in the box. 75 â€"" 3. 5y â€"" 4y = 4y 6.
Related Questions
UHM YES AGAIN BECAUSE IMMA TRYNNA GET GOOD GRADES :)

Answers
Answer:
I think it's qualitative
Step-by-step explanation:
My best guess
Answer:
i think it would be d? im not sure
Step-by-step explanation:
A news organization interested in chronicling winter holiday travel trends conducted a survey. Of the 96 people surveyed in the eastern half of a country, 42 said they fly to visit family members for the winter holidays. Of the 108 people surveyed in the western half of the country, 81 said they fly to visit family members for the winter holidays.
Use a calculator to construct a 99% confidence interval for the difference in population proportions of people in the eastern half of a country who fly to visit family members for the winter holidays and people in the western half of a country who fly to visit family members for the winter holidays. Assume that random samples are obtained and the samples are independent.
Round your answers to three decimal places.
Answers
We are 99% confident that the true difference in population proportions of people in the eastern half of the country who fly to visit family members for the winter holidays and people in the western half of the country who fly to visit family members for the winter holidays is somewhere between -0.422 and -0.114.
Next, we need to calculate the standard error of the difference in sample proportions. This gives us an idea of how much the sample difference in proportions can be expected to vary from the true population difference in proportions. We use the following formula to calculate the standard error:
√((p₁(1-p₁)/n₁)+(p₂(1-p₂)/n₂))
where p₁ and p₂ are the sample proportions, and n₁ and n₂ are the sample sizes. Plugging in the values we have, we get a standard error of 0.094.
Now that we have the sample proportions and the standard error, we can use a confidence interval formula to calculate the range of values that we can be confident contains the true population difference in proportions. For a 99% confidence interval, the formula is:
(sample proportion 1 - sample proportion 2) +/- (critical value x standard error)
The critical value is obtained from a t-distribution table, with degrees of freedom equal to the smaller of (n1-1) and (n2-1). For a 99% confidence level and 44 degrees of freedom, the critical value is 2.689.
Plugging in the values we have, we get a confidence interval of:
0.438 - 0.75 +/- 2.689 x 0.094
= -0.422 to -0.114
To know more about confidence interval here
https://brainly.com/question/24131141
#SPJ4
Aflati al 2013 lea termen al unei progresii aritmetice cu termenul al treilea egal cu 12 si diferenta a doi termeni consecutivi, 4.
Answers
Răspuns:
8052
Explicație pas cu pas:
Al treilea termen al unei progresii aritmetice:
T (n) = a + (n - 1) d
Unde ;
a = primul termen; d = diferență comună = 4; n = al treilea termen (numărul termenului)
Al treilea (3) termen:
T (3) = a + (3-1) 4
T (3) = 12
12 = a + 2 (4)
12 = a + 8
12 - 8 = a
4 = a
Prin urmare, primul termen = a
Al 2013-lea mandat;
T (2013) = a + (2013-1) d
T (2013) = 4 + (2012) 4
T (2013) = 4 + 8048
= 8052
the question is in the above
please write your answer with explaination
thank you so much and have a great day

Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
we know that volume of a sphere is :
\( \boxed{ \boxed{ \frac{4}{3} \pi {r}^{3} }}\)so, let's solve for radius (r) :
\( \dfrac{4}{3} \pi {r}^{3} = 288 \pi\)\(r {}^{3} = 288 \pi \times \dfrac{3}{4 \pi} \)\(r {}^{3} = 72 \times 3\)\(r {}^{3} = 216\)\(r = \sqrt[3]{216} \)\(r = 6\)value of radius (r) = 6 units
is 3:5 and 1:3 equivalent ?
Answers
Answer:
No they are not equivalent
Step-by-step explanation:
Recall 3:5 ratio is the same as 3/8 or 5/8
ratio has to do with the sum of the two values
therefore; 3:5
3+5=8
and to know if it's equivalent we say
the first value divided by the total value gotten
which is 3/8
then apply it in the second value which is 5/8
Dividing it through you will not get 1/3
At time t= 0, a storage tank is empty and begins filling with water. For t > 0 hours, the depth of the water in the tank is increasing at a rate of W (t) feet per hour. Which of the following is the best interpretation of the statement W' (2) > 3?
a. Two hours after the tank begins filling with water, the depth of the water is increasing at a rate greater than 33 feet per hour.
b. Over the first two hours after the tank begins filling with water, the depth of the water is always increasing at a rate greater than 3 feet per hour.
c. Two hours after the tank begins filling with water, the rate at which the depth of the water is rising is increasing at a rate greater than 3 feet per hour per hour.
d. Over the first two hours after the tank begins filling with water, the rate at which the depth of the water is rising is always increasing at a rate greater than 33 feet per hour per hour.
Answers
The given function is the rate of change of the water depth. therefore,
W'(t) is the second derivative.
The correct option is; d. Two hours after the tank begins filling with water, the rate at which the depth of the water is rising is increasing at a rate greater than 3 feet per hour per hour.Reasons:
The volume of water in the tank is 0 at time t = 0 (the tank is empty)
The function that gives the rate at which the depth of water in the tank is
increasing at time t > 0 is W(t).
Where;
t = The time in hours
Therefore;
W'(t), the derivative of the function of the rate at which the water in the
tank is increasing in feet per hour is the rate of increase of W(t).
Which gives;
W'(2) = The rate of change of the rate at which the water level is rising (second derivative) two hours after begins to fill with water, per hour per hour.
Therefore;
W'(2) > 3 = Two hours after the tank begins filling with water, the rate at which the depth of the water is rising is increasing at a rate greater than 3 feet per hour per hour.Learn more about second derivative here:
https://brainly.com/question/10305010
Find the area of the circle and enter your answer below. Leave Pl in the answer (do not multiply by Pl) Area = πm2 6 m
Answers
Answer:
36π
Step-by-step explanation:
Since we are given the equation and the value for m, we can plug it into the equation to solve for the area:
Area = πm²
Area = π6²
Area = 36π
You online store only sells one item, in either regular or deluxe version.
Because of high demand and restricted supply, you restrict each customer to buying 1 item - either buying the regular version of that item, or the deluxe version of that item, but not both.
On a typical day, you have 177 customers visit your online store. Each customer has a 0.29 chance of purchasing an item. If a customer purchases an item, there is a 9% chance they buy the regular item for $5.08 and if they do not buy the regular item, then they buy the deluxe item for $23.34.
Assume each customer makes their purchase decision independently of all other customers, and each customer has the same chance of purchasing the item.
What is your expected daily sales?
Answers
The expected daily sales for your online store are approximately $1196.28.
To calculate the expected daily sales, we need to multiply the number of customers by the probability of each customer purchasing an item and then sum up the expected sales for each type of item.
Given:
- Number of customers: 177
- Probability of a customer purchasing an item: 0.29
- Probability of buying the regular item: 0.09
- Probability of buying the deluxe item: 1 - 0.09 = 0.91
- Price of the regular item: $5.08
- Price of the deluxe item: $23.34
Let's calculate the expected daily sales:
Expected sales of regular items = Number of customers * Probability of purchasing * Probability of buying the regular item * Price of the regular item
Expected sales of deluxe items = Number of customers * Probability of purchasing * Probability of buying the deluxe item * Price of the deluxe item
Expected daily sales = Expected sales of regular items + Expected sales of deluxe items
Expected sales of regular items = 177 * 0.29 * 0.09 * $5.08 ≈ $85.74
Expected sales of deluxe items = 177 * 0.29 * 0.91 * $23.34 ≈ $1110.54
Expected daily sales = $85.74 + $1110.54 ≈ $1196.28
Therefore, the expected daily sales for your online store are approximately $1196.28.
Learn more about sales here:
brainly.com/question/15098610
#SPJ4
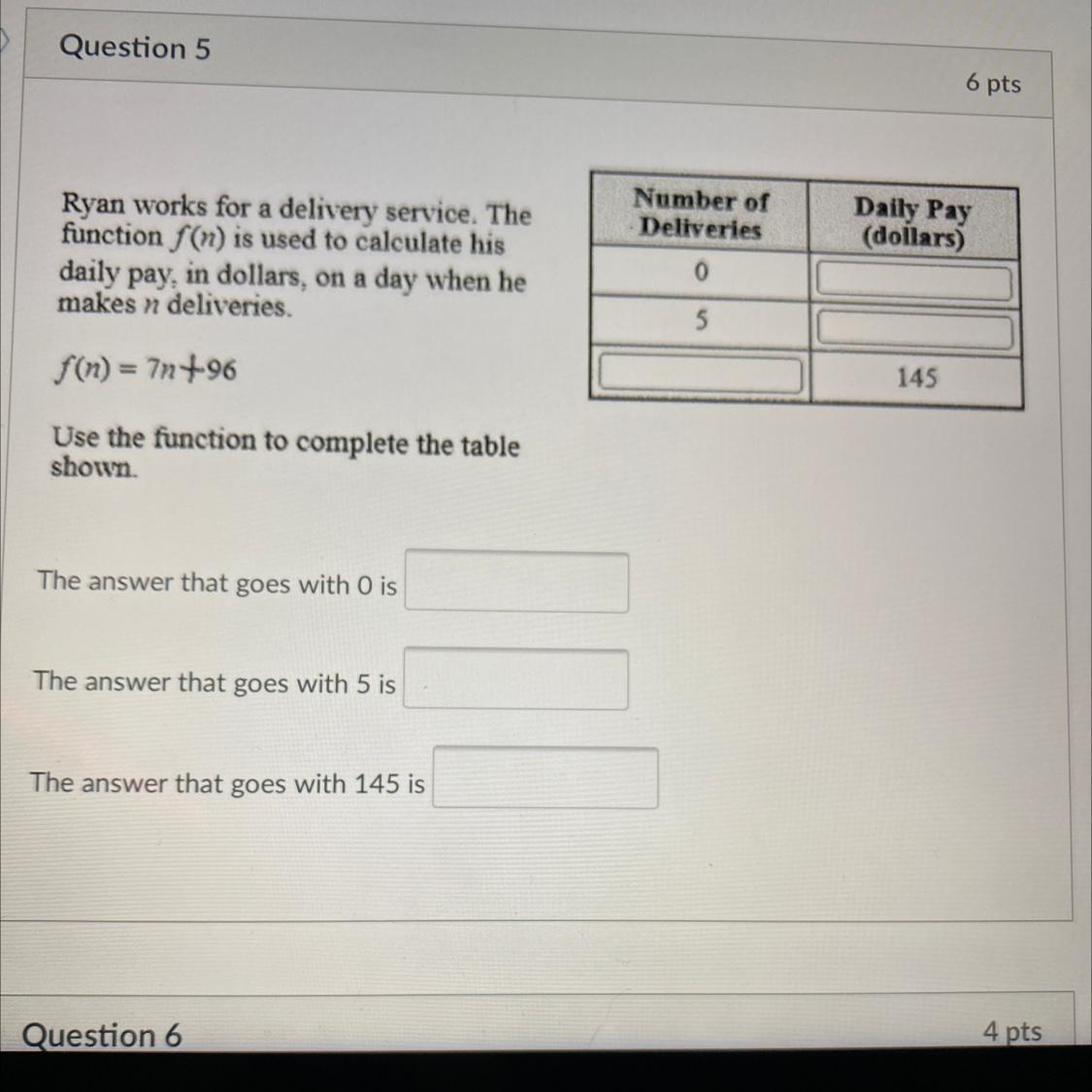
Number of
Deliveries
Daily Pay
(dollars)
0
Ryan works for a delivery service. The
function f(n) is used to calculate his
daily pay, in dollars, on a day when he
makes n deliveries.
f(n) = 7n4.96
5
145
Use the function to complete the table
shown.
Answers
Answer:
1)96
2)131
3)7
Step-by-step explanation:
please mark me as brainlest and follow me
can you help me find slope and y intercept

Answers
Answer:
it's right in front of you actually. the y intercept is negative 1/7 and the slope is 1/7
Answer:
your slope 1/7x and your y-int is -1/7. Hope this helps!
Step-by-step explanation:
solve the differential equation by variation of parameters. y'' + y = cos2(x)
Answers
Answer:
\(y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}}}\)
Step-by-step explanation:
Given the second-order differential equation, \(y'' + y = cos2(x)\), solve it using variation of parameters.
(1) - Solve the DE as if it were homogenous and find the homogeneous solution\(y'' + y = cos2(x) \Longrightarrow y'' + y =0\\\\\text{The characteristic equation} \Rightarrow m^2+1=0\\\\m^2+1=0\\\\ \Longrightarrow m^2=-1\\\\\ \Longrightarrow m=\sqrt{-1} \\\\\Longrightarrow \boxed{m=\pm i} \\ \\\text{Solution is complex will be in the form} \ \boxed{y=c_1e^{\alpha t}\cos(\beta t)+c_2e^{\alpha t}\sin(\beta t)} \ \text{where} \ m=\alpha \pm \beta i\)
\(\therefore \text{homogeneous solution} \rightarrow \boxed{y_h=c_1\cos(x)+c_2\sin(x)}\)
(2) - Find the Wronskian determinant
\(|W|=\left|\begin{array}{ccc}y_1&y_2\\y'_1&y'_2\end{array}\right| \\\\\Longrightarrow |W|=\left|\begin{array}{ccc}\cos(x)&\sin(x)\\-sin(t)&cos(x)\end{array}\right|\\\\\Longrightarrow \cos^2(x)+\sin^2(x)\\\\\Longrightarrow \boxed{|W|=1}\)
(3) - Find W_1 and W_2
\(\boxed{W_1=\left|\begin{array}{ccc}0&y_2\\g(x)&y'_2\end{array}\right| and \ W_2=\left|\begin{array}{ccc}y_2&0\\y'_2&g(x)\end{array}\right|}\)
\(W_1=\left|\begin{array}{ccc}0&\sin(x)\\\cos^2(x)&\cos(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_1= -\sin(x)\cos^2(x)}\\\\W_2=\left|\begin{array}{ccc}\cos(x)&0\\ -\sin(x)&\cos^2(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_2= \cos^3(x)}\)
(4) - Find u_1 and u_2
\(\boxed{u_1=\int\frac{W_1}{|W|} \ and \ u_2=\int\frac{W_2}{|W|} }\)\
u_1:
\(\int(\frac{-\sin(x)\cos^2(x)}{1}) dx\\\\\Longrightarrow-\int(\sin(x)\cos^2(x)) dx\\\\\text{Let} \ u=\cos(x) \rightarrow du=-sin(x)dx\\\\\Longrightarrow\int u^2 du\\\\\Longrightarrow \frac{1}{3}u^3\\ \\\Longrightarrow \boxed{u_1=\frac{1}{3}\cos^3(x)}\)
u_2:
\(\int\frac{\cos^3(x)}{1}dx\\ \\\Longrightarrow \int \cos^3(x)dx\\\\ \Longrightarrow \int (\cos^2(x)\cos(x))dx \ \ \boxed{\text{Trig identity:} \cos^2(x)=1-\sin^2(x)}\\\\\Longrightarrow \int[(1-\sin^2(x)})\cos(x)]dx\\\\\Longrightarrow \int \cos(x)dx-\int (\sin^2(x)\cos(x))dx\\\\\Longrightarrow \sin(x)-\int (\sin^2(x)\cos(x))dx\\\\\text{Let} \ u=\sin(x) \rightarrow du=cos(x)dx\\\\\Longrightarrow \sin(x)-\int u^2du\\\\\Longrightarrow \sin(x)-\frac{1}{3} u^3\)\
\(\Longrightarrow \boxed{u_2=\sin(x)-\frac{1}{3} \sin^3(x)}\)
(5) - Generate the particular solution
\(\text{Particular solution} \rightarrow y_p=u_1y_1+u_2y_2\)
\(\Longrightarrow y_p=(\frac{1}{3}\cos(x))(\cos(x))+(\sin(x)-\frac{1}{3} \sin^3(x))(\sin(x))\\\\ \Longrightarrow y_p=\frac{1}{3}\cos^4(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)\\\\\Longrightarrow \boxed{y_p=\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}\)
(6) - Form the general solution
\(\text{General solution} \rightarrow y_{gen.}=y_h+y_p\)
\(\boxed{\boxed{y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}}}\)
Thus, the solution to the given DE is found where c_1 and c_2 are arbitrary constants that can be solved for given an initial condition. You can simplify the solution more if need be.
Suppose a department contains 10 men and 15 women. a) How many ways are there to form a committee of 6 people from the department? Explain your answer. b) How many ways are there to form a committee of 6 people from the department, if the number of men in the committee is equal to the number of females in the committee? Explain your answer. c) How many ways are there to form a committee of 6 people from the department, if the number of men in the committee is less than the number of females in the committee? Explain your answer.
Answers
a) The number of ways to form a committee of 6 people from the department is 177,100.
b) The number of ways to form a committee of 6 people with an equal number of men and women is 54,600.
c) The number of ways to form a committee of 6 people with more women than men is 91,455.
a) To form a committee of 6 people from the department, we can choose 6 individuals from a total of 25 people (10 men + 15 women). The order in which the committee members are chosen does not matter, and we are not concerned with any specific positions within the committee. Therefore, we can use the concept of combinations.
The number of ways to choose 6 people from a group of 25 is given by the combination formula:
C(25, 6) = 25! / (6! * (25 - 6)!) = 25! / (6! * 19!) = 177,100
Therefore, there are 177,100 ways to form a committee of 6 people from the department.
b) In this case, we need to choose an equal number of men and women for the committee. We can select 3 men from the available 10 men and 3 women from the available 15 women. Again, the order of selection does not matter.
The number of ways to choose 3 men from 10 is given by the combination formula:
C(10, 3) = 10! / (3! * (10 - 3)!) = 10! / (3! * 7!) = 120
Similarly, the number of ways to choose 3 women from 15 is:
C(15, 3) = 15! / (3! * (15 - 3)!) = 15! / (3! * 12!) = 455
To find the total number of ways to form a committee with an equal number of men and women, we multiply these two combinations:
Total = C(10, 3) * C(15, 3) = 120 * 455 = 54,600
Therefore, there are 54,600 ways to form a committee of 6 people with an equal number of men and women.
c) In this case, we need to form a committee with more women than men. We can choose 1 or 2 men from the 10 available men and select the remaining 6 - (1 or 2) = 5 or 4 women from the 15 available women.
For 1 man and 5 women:
Number of ways to choose 1 man from 10: C(10, 1) = 10
Number of ways to choose 5 women from 15: C(15, 5) = 3,003
For 2 men and 4 women:
Number of ways to choose 2 men from 10: C(10, 2) = 45
Number of ways to choose 4 women from 15: C(15, 4) = 1,365
The total number of ways to form a committee with more women than men is the sum of these two cases:
Total = (Number of ways for 1 man and 5 women) + (Number of ways for 2 men and 4 women)
= 10 * 3,003 + 45 * 1,365
= 30,030 + 61,425
= 91,455
Therefore, there are 91,455 ways to form a committee of 6 people with more women than men.
To know more about number of ways, refer here:
https://brainly.com/question/30649502
#SPJ4
a ball dropped from rest and falls for 8 seconds
whats the final velocity
and whats te average velocity
how far did it fall
Answers
How many solutions are possible for a system of two quadratic equations?
Answers
A system of two quadratic equations can have no solution, one solution, or infinitely many solutions.
A system of two quadratic equations can have three possible scenarios regarding the number of solutions: no solution, one solution, or infinitely many solutions.
No solution: In this case, the two quadratic equations do not intersect or intersect at points that are not common. Geometrically, this represents two parabolas that are either completely separate or have no points of intersection. Algebraically, there is no value for the variables that simultaneously satisfies both equations.
One solution: This occurs when the two quadratic equations intersect at a single point. Geometrically, this represents two parabolas that intersect at a specific point. Algebraically, there is one unique solution that satisfies both equations simultaneously.
Infinitely many solutions: This happens when the two quadratic equations are essentially the same or are multiples of each other. Geometrically, this represents two parabolas that overlap completely or coincide. Algebraically, every point on the parabola(s) satisfies both equations.
The possibility of each scenario depends on the specific equations involved in the system. By manipulating the coefficients and constants in the equations, we can control the number of solutions.
Learn more about quadratic equations here:
https://brainly.com/question/30098550
#SPJ11
Please help me i am struggling only do the left side

Answers
Answer:
1. Y = -1/4x + 1
3. Y = 2/5x + 1
5. Y = 4/5x + 5
7. Y = -x + 5
9. Y = -5/2x - 16
Step-by-step explanation:
Find the slope using the formula
Use the slope and one of the points to find the y-intercept
Once you know the value for m and the value for b, you can plug these into the slope-intercept form of a line (y = mx + b) to get the equation for the line.
Explain why a+b=d because I don’t understand

Answers
Answer:
a and b connect to d in the slope
Step-by-step explanation:
Answer:
Aight mate
Step-by-step explanation:
So every triangles angles will add up to 180 degrees no matter the triangle. Now a circle is 360 and a line is 180. Look at the line that A and C are on this line equals 180. So angle c and d added together make 180 and angles a b and c added together make 180. so if a+b+c = c+d then a+b=c. I hope thaqtmakes sense.
Peter bought three Note 20 Android phones costing 1050 dollars each. If he had 4000 dollars in his checking account, write a numerical expression and then find his balance after he paid for the phones. Solution
Answers
Answer:
4000 - 3(1050)
= 850
Step-by-step explanation:
Start with the 4000 that's in the account. Then subtract 3(1050) which represents 3×1050, the cost of three phones.
4000 - 3(1050)
= 4000 - 3150
= 850
He has 850 left in his account.
The philanthropic organization in Exercise 1 expects about a 5%success rate when they send fundraising letters to the people on their mailing list. In Exercise 1 you looked at the histograms showing distributions of sample proportions from 1000 simulated mailings for samples of size and The sample statistics from each simulation were as follows:a) According to the Central Limit Theorem, what should the theoretical mean and standard deviations be for these sample sizes?b) How close are those theoretical values to what was observed in these simulations?c) Looking at the histograms in Exercise at what sample size would you be comfortable using the Normal model as an approximation for the sampling distribution?d) What does the Success/Failure Condition say about the choice you made in part c?
Answers
The Normal model is a good approximation for the sampling distribution.
a) According to the Central Limit Theorem, the theoretical mean and standard deviation for a sample size of 20 should be 0.05 and 0.02, respectively. For a sample size of 100, the theoretical mean and standard deviation should be 0.05 and 0.01, respectively.
b) The observed mean and standard deviation for a sample size of 20 was 0.052 and 0.021, respectively. For a sample size of 100, the observed mean and standard deviation was 0.051 and 0.012, respectively. These values are fairly close to the theoretical values.
c) Looking at the histograms in Exercise 1, I would be comfortable using the Normal model as an approximation for the sampling distribution at a sample size of 100.
d) The Success/Failure Condition states that the sample size should be large enough for the sampling distribution of the sample proportions to be approximately normal. Since I chose a sample size of 100, which satisfied the condition, I can be confident that the Normal model is a good approximation for the sampling distribution.
The sample size of 100 is large enough for the sampling distribution of the sample proportions to be approximately normal, and the observed mean and standard deviation is close to the theoretical values. Therefore, the Normal model is a good approximation for the sampling distribution.
Learn more about sampling distribution here:
https://brainly.com/question/30007465
#SPJ4
Deepa needed to get her computer fixed. She took it to the repair store. The technician at the store worked on the computer for 4. 25 hours and charged her $167 for parts. The total was $655. 75. Write and solve an equation which can be used to determine xx, the cost of the labor per hour.
Answers
The cost of the labor per hour is 115 hours.
The equation is going to be:
4.25x + 167 = 655.75
your x is going to be:115
The duration was 4.25 hours.
The parts cost 167.
Cost in full: 655.75
so the price per hour is x.
As a result, when you write your equation, the total number of hours (multiplied by the cost per hour) will be added to the cost of the parts, and the sum of these two amounts will be your total cost.
In order to solve the problem, you must deduct the cost of each component from the total cost. This should give you the following result: 4.25x = 488.75
After that, divide 4.25 by each side as you normally would.
The cost of labor per hour follows. 115
Know more about Equations at:
https://brainly.com/question/26310043
#SPJ4
look at the figure at the right . Explain one thing that representing the area of the figure as 9(X+3)-6x tells you about the situation. Then write an equivalent expression for the area . Explain what information is in your expression that is not in 9(x+3)-6x.
Answers
The figure's area is calculated by subtracting the entire rectangle from the empty rectangle.
Write an equivalent expression for the area?The area of a rectangle in a two-dimensional plane is the space that it occupies. A rectangle is a quadrilateral, a kind of two-dimensional object with four sides and four vertices. The rectangle's four sides are all right angles or exactly 90 degrees. The rectangle's opposing edges are equal and parallel to one another. It should be observed that a parallelogram also has equal and parallel opposite sides, but the angles are not exactly 90 degrees.
The following is the solution for the figure's area:
9 (x+3) - 6x.
The entire figure's area has been described as 9 (x+3).
where 9 is the length of the rectangle and (x+3) = (x+1.5+1.5) is the width of the rectangle.
Currently, the empty space between has been assigned the value 6x.
where the rectangle's edges are 6 and x.
Therefore, the size of the figure is the entire rectangle less the empty rectangle.
To know more about rectangle, visit:
https://brainly.com/question/25292087
#SPJ1
The complete question is:
Look at the figure at the right. Explain one thing that representing the area of the figure as 9(X+3)-6x tells you about the situation. Then write an equivalent expression for the area. Explain what information is in your expression that is not in 9(x+3)-6x.

Solve for C⁰... photo above

Answers
Answer:
c = 9
Step-by-step explanation:
Since angle d and 59 are on a right angle (indicated by the small square)
We can equate the sum of these angles to 90:
d+59=90
Now we subtract 59 from both sides:
d+59-59=90-59
d=31
Since angles d,c and 140 are on a straight line we can equate the sum of these 3 to 180:
c+d+140=180
Substitute d with 31 from previous working out:
c+31+140=180
Simplify:
c+171=180
Subtract 171 from both sides:
c+171-171=180-171
Simplify:
c= 9
7) if 370x9 is a
multiple of 3 where x is a digit, what are the value of x
Answers
Answer:
A number is a multiple of 3 if the sum of the digit equal to a number divided by 3
so, 3+7+0+9=19
21, 24, 27 are numbers that is a multiple of 3
So, the number are
19+x=21
x=2
19+x=24
x=5
19+x=27
x=8
Answer:
1110
Step by step explanation:
370×9=3330
in the question it's said that 370 ×9 is a multiple of 3
i.e,3330 is a multiple of 3.
3 multiplied with x = 3330
x = 3330/3
=1110
Use interval notation to represent the domain and range of the following functions. Hint: Start by thinking about the meaning of each function's input and output quantities and the values those quantities can assume.
a. Determine the domain and range of the cos function.
。 Domain:
Preview
• Range:
b. Determine the domain and range of the sin
Preview
function.
。 Domain:
Preview
。 Range:
Preview
c. Determine the domain and range of the tan
function.
• Domain:
Preview
。 Range:
Preview
Answers
c) The range of the tangent function is all real numbers. This can be represented as (-∞, ∞) in interval notation
a. The domain of the cosine function (cos) is all real numbers. This can be represented as (-∞, ∞) in interval notation.
The range of the cosine function is [-1, 1]. This can be represented as [-1, 1] in interval notation.
b. The domain of the sine function (sin) is all real numbers. This can be represented as (-∞, ∞) in interval notation.
The range of the sine function is [-1, 1]. This can be represented as [-1, 1] in interval notation.
c. The domain of the tangent function (tan) is all real numbers except the values where the function is undefined, which occur when the input angle is equal to (2k + 1)π/2, where k is an integer. This can be represented as (-∞, (2k + 1)π/2) ∪ ((2k + 1)π/2, ∞) in interval notation.
To know more about interval visit;
brainly.com/question/11051767
#SPJ11
Find the 12th term -7, -3, 1,
Answers
Answer:
\( \sf \: 12th \: term = 37\)
Step-by-step explanation:
Common difference (d) is,
→ d = a2 - a1
→ d = -3 - (-7)
→ d = -3 + 7
→ [ d = 4 ]
Now the 12th term will be,
→ a1 + (d × (n - 1))
→ -7 + (4 × (12 - 1))
→ -7 + (4 × 11)
→ -7 + 44
→ 37 => 12th term
Hence, the answer is 37.
I need help solving this

Answers
Answer:
the answer is in the picture

1. Jervane is planning on buying a coffee and several donuts for a road trip. She wants to spend no more than $20 in total. Coffee costs $3 and donuts are $2 each. Write and solve an inequality to determine the maximum number of donuts that Jervane can buy. Be sure to include units on your answer.( I'll give you brainless)
Answers
Answer: 8
Step-by-step explanation: Given:
Total money Jervane can spend = $20.
Cost of a coffee = $3.
Cost of a donut = $2.
To find: Maximum number of donuts Jervane can buy.
Solution:
Let the number of donuts she can buy be .
She wants to spend no more than $20 in total.
So,
As the number of donuts can only be a natural number.
Hence, the maximum number of donuts that Jervane can buy are 8.
Iris's checking account pays simple interest at 4% per year. She has $180 in her account. Write a linear function to model the amount of money in her checking account at any time t.
A(t)=
Answers
The amount of money in Iris's checking account can be modeled by a linear function of the form:
y = mt + b
where y is the amount of money in the account, t is the time (measured in years), m is the rate of interest, and b is the initial amount in the account.
In this case, we have m = 0.04 (since the interest rate is 4% per year) and b = 180 (since that's the initial amount in the account). Therefore, the linear function that models the amount of money in Iris's checking account at any time t is:
y = 0.04t + 180
For example, if t = 5 (years), then the amount of money in Iris's checking account is 0.04 * 5 + 180 = 198 dollars.
NEEDING HELP ASAP!
*CLICK ON PHOTO*
!SHOW ALL WORK!

Answers
-6x-2y=42
x-y=-15
Multiply x-y=-15 by 6 ( eliminate the x first)
6(x-y)=6(-15)
(6)(x)=6x
(6)(-y)=-6y
6(-15)=-90
-6x-2y=42
6x-6y=-90
eliminate x the systems of equations by subtracting
-6x+6x-2y+-6y=42-90
-2y-6y=42-90
-8y=-48
divide both sides by -8 to get y by itself
-8y/-8=-48/8
y=6
Find x by substitution method
use y=6 into one of the system of equations
x-y=-15
x-6=-15
move -6 to the other side
sign changes from -6 to +6
x-6+6=-15+6
x=-15+6
x=-9
answer:
(-9,6)
Morgan's swim team practice is 90 minutes long. She spends 40% of the time doing backstroke. How many minutes does Morgan spend doing backstroke?
Answers
Answer:
She spends 36 minutes doing backstroke.
Step-by-step explanation:
\(0.4\) × \(90 = 36\)
There is a 15% increase in tuition at UT for next fall. If the current tuition is $3,500 per semester, which equation could be used to find x, the new tuition for the fall? A. 0.15 • 3500 = x B. 1.15 • 3500 = xC. 0.85 • 3500 = x D. (15/100) = (x/3500)
Answers
The new tuition for the fall will be $4,025 per semester. This is exactly what we get by using equation B, since: 1.15 • 3500 = 4025
The correct equation to find the new tuition for the fall is: B. 1.15 • 3500 = x
Here's why: The problem states that there is a 15% increase in tuition, which means that the new tuition will be the current tuition plus 15% of the current tuition. Mathematically, we can represent this as:
new tuition = current tuition + 15% of current tuition
Using x to represent the new tuition, and 3500 to represent the current tuition, we can write this equation as:
x = 3500 + 0.15(3500)
Simplifying the right side, we get:
x = 3500 + 525
x = 4025
Therefore, the new tuition for the fall will be $4,025 per semester. This is exactly what we get by using equation B, since: 1.15 • 3500 = 4025
Learn more about “ new tuition “ visit here;
https://brainly.com/question/14658656
#SPJ4