solve using elimination 3x+5y=4; -3x+y=8
Answers
Answer:
x=-2
y=2
Step-by-step explanation:
-3x+y=8
+3x +3x
y=8+3x
3x+5(8+3x)=4
3x+40+15x=4
18x+40=4
-40 -40
18x=-36
x=-2
-3(-2)+y=8
6+y=8
-6 -6
y=2
Related Questions
Joan descends down a
mountain 140 feet in 5
minutes. What was the change
in altitude per minute?
Answers
Answer:
28
Step-by-step explanation:
140 / 5 = 28
Write an equation in slope-intercept form of the line that passes through (-1, 4) and (0, 2)
Answers
Answer:
y = -2x + 2
General Formulas and Concepts
Pre-Alg
Order of Operations: BPEMDASAlgebra I
Slope-Intercept Form: y = mx + b
m - slope b - y-interceptSlope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)
Step-by-step explanation:
Step 1: Define
Point (-1, 4)
y-intercept (0, 2)
Step 2: Find slope m
Substitute: \(m=\frac{2-4}{0+1}\)Subtract/Add: \(m=\frac{-2}{1}\)Divide: \(m=-2\)Step 3: Write linear equation
y = -2x + 2
Please help meeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Answer:
a) x = 1.5 or x = -0.3
b) x = 5 or x = -8
Explanation:
Quadratic formula:
\(\sf x = \dfrac{ -b \pm \sqrt{b^2 - 4ac}}{2a} \quad when \:\: ax^2 + bx + c = 0\)
Here given equation: 5x² - 6x - 2 = 0
Identify variable constants: a = 5, b = -6, c = -2
Putting these values into equation:
\(\sf x = \dfrac{ -(-6) \pm \sqrt{(-6)^2 - 4(5)(-2)}}{2(5)}\)
\(\sf x = \dfrac{ 6 \pm \sqrt{36 + 40}}{10}\)
\(\sf x = \dfrac{ 6 \pm \sqrt{76}}{10}\)
\(\sf x = \dfrac{ 3\pm \sqrt{76}}{5}\)
\(\sf x = \dfrac{ 3+ \sqrt{76}}{5} \quad or \quad \dfrac{ 3- \sqrt{76}}{5}\)
In one decimal point:
\(\sf x = 1.5 \quad or \quad -0.3\)
b) Here use "middle term split" method
⇒ x² + 3x = 40
relocate
⇒ x² + 3x - 40 = 0
The factors of 40 are 8 and 5
⇒ x² + 8x - 5x - 40 = 0
factor common terms
⇒ x(x + 8) - 5(x + 8) = 0
collect into groups
⇒ (x - 5)(x + 8) = 0
set to zero
⇒ x - 5 = 0 or x + 8 = 0
relocate
⇒ x = 5 or x = -8
Step-by-step explanation:
a) The quadratic formula can help find answers to a quadratic equation when it is equal to 0. The formula is \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\) for a quadratic equation of the form \(ax^2+bx+c=0\).
In this question, a is 5, b is -6, and c is -2. Let's put them in the equation and solve.
\(x=\frac{6\pm\sqrt{(-6)^2-4(5)(-2)}}{2(5)}\\x=\frac{6\pm\sqrt{36+40}}{10}\\x=\frac{6\pm\sqrt{76}}{10}\\x=\frac{6\pm2\sqrt{19}}{10}\\x=\frac{3\pm\sqrt{19}}{5}\)
This means that the value of x is both \(\frac{3+\sqrt{19}}5\) and \(\frac{3-\sqrt{19}}5\), since both values make x equal to 0. Putting both into the calculator, we get that \(x=1.5\) or \(x=-0.3\).
b) We can easily solve this equation using factoring, which turns a quadratic into two factors, and finds the solutions by setting both to 0. This will only work if the quadratic is equal to 0.
\(x^2+3x-40=0\)
Now, we have to find two numbers that add to 3 and multiply to -40. The numbers 8 and -5 work, as 8-5=3 and 8*-5 is -40.
we can now make our factors x+8 and x-5
\((x+8)(x-5)=0\)
If two numbers, say A and B, are being multiplied and equal 0, then either A is 0, or b is 0, or both. Similarly, if x+8 and x-5 are being multiplied and equal 0, either x+8 = 0, or x-5=0.
\(x+8=0\\x=-8\) \(x-5=0\\x=5\)
This makes our solutions x=-8 and x=5.
If you are not familiar with factoring or the process I have went through above, I highly recommend learning about it.
20. sarah and gabe are sharing a sheet of stickers. Sara has 2/7 of the sheet. Gabe has 1/4 of the sheet. What fraction of the sheet do sara and gabe have together?
Answers
Explanation:
Based on the given conditions, formulate 2/7+1/4
Expand the fraction to get the least common denominator 2x4/7x4 + 7/4x7
Calculate the product or quotient 8/7x4 + 7/4x7
Calculate the product or quotient 8/28 + 7/4x7
Calculate the product or quotient 8/28+7/28
Write the numerators over common denominator 8+7/28
Calculate the sum or difference 15/28
Convert to fraction 15/28
So the answer is 15/28
Hope that helped!!!!
To add two fraction together we should have the same denominator
We have to multiply Sarah’s fraction by 4 and gsbe’s by 7
Sarah:8/28
Gabe: 7/28
8/28+7/28=15/28
−2p + 23 = 15
What does p =
Answers
Answer:
look at the picture .................

mPQ = 121°. What is m<POQ? Enter your answer in the box.

Answers
Reason:
The central angle is the same measure as the arc it subtends.
Question text Level and Trend in a Time Series is estimated by- Select one: a. Moving Average b. Simulation method c. Regression analysis d. Covariance analysis e. Correlation Analysis
Answers
(C) Regression analysis is the statistical method commonly used to estimate the level and trend in a time series by modeling the relationship between the data and independent variables.
Regression analysis is the statistical method used to estimate the level and trend in a time series. Time series data represents observations taken at different points in time and is commonly used to analyze trends and patterns over time.
Regression analysis allows us to model the relationship between a dependent variable (in this case, the time series data) and one or more independent variables (such as time or other relevant factors). By using regression analysis, we can identify the underlying trend in the time series and estimate its level.
The regression model captures the relationship between the dependent variable (the time series) and the independent variable(s) by fitting a line or curve that best represents the data. This line or curve helps to identify the overall trend and level of the time series.
While moving average, simulation method, covariance analysis, and correlation analysis are useful techniques in analyzing time series data, they are not specifically designed to estimate the level and trend in a time series. Therefore, (C) regression analysis is the most appropriate method for estimating the level and trend in a time series.
Learn more about Regression analysis here:
https://brainly.com/question/31860839
#SPJ11
what is the standard error of the sampling distribution of the sample mean?
Answers
The standard error of the sampling distribution of the sample mean is a measure of the variability of sample means that would be obtained from repeated sampling of the same population. It is calculated as the standard deviation of the sampling distribution of the sample mean.
In other words, the standard error reflects how much the sample means from different samples would be expected to vary from the true population mean. As the sample size increases, the standard error decreases because the sample means become more representative of the population mean. Conversely, as the sample size decreases, the standard error increases because the sample means become less representative of the population mean.
The formula for calculating the standard error of the sample mean is:
Standard Error = Standard Deviation / Square root of Sample Size
where the standard deviation is the variability of the population and the sample size is the number of observations in the sample.
The standard error is an important concept in statistical inference because it is used to calculate confidence intervals and hypothesis tests for population means based on sample means. A larger standard error indicates that there is more uncertainty in the estimate of the population mean, and a smaller standard error indicates that the estimate is more precise. In conclusion, the standard error of the sampling distribution of the sample mean is a measure of the variability of sample means that would be obtained from repeated sampling of the same population. It is a key concept in statistical inference and is used to calculate confidence intervals and hypothesis tests for population means based on sample means.
To know more about statistical inference click here:
brainly.com/question/29753183
#SPJ4
Lanthanum -144 becomes cerium- 144 when it undergoes a beta decay (write an equation)
Answers
Beta decay is a type of radioactive decay that occurs in certain atomic nuclei. It involves the transformation of a neutron or proton within the nucleus into the other.
In the case of Lanthanum-144 (La-144), a neutron undergoes beta decay to convert into a proton, resulting in the formation of Cerium-144 (Ce-144).
The equation for the beta decay of La-144 into Ce-144 is as follows:
La-144 → Ce-144 + β¯
In this equation, the La-144 nucleus decays into the Ce-144 nucleus. To conserve charge, a beta particle (β¯) is emitted. The beta particle can be either an electron (β-) or a positron (β+), depending on the specific type of beta decay occurring in the nuclide.
Learn more about Beta decay here : brainly.com/question/21370162
#SPJ11
Can somebody please answer this question but with showing your work, thank you!!!
I WILL GIVE BRAINLIEST TO ANYONE WHO CAN SOLVE THIS FAST AND CORRECTLY :DDDD

Answers
Answer:
decrease 1°C
Step-by-step explanation:
Solution:
\(-4-(-3)\\ =-4+3\\ =-1\)
decrease 1°c
Answer:
the answer is a positive 1 degrees
Step-by-step explanation:
Ms. Zheng drove 7 miles to a restaurant for lunch, she then drove 2 miles for
shopping, finally she drove 8 miles back home. How many miles did she drive in total?
I NEED THE ANSWER FAST PLEASE…..
Answers
Kelsey knit a total of 6 centimeters of scarf over 2 nights. After 4 nights of knitting, how many centimeters of scarf will Kelsey have knit in total? Assume the relationship is directly proportional.
Answers
Answer:
\(12\) cm
Step-by-step explanation:
If Kelsey knit a total of \(6\) cm of scarf over \(2\) nights, then we know that she can knit \(\frac{6}{2}=3\) cm each night. Therefore, after \(4\) nights of knitting, Kelsey would have knit a total of \(3*4=12\) cm of scarf in total. Hope this helps!
The exchange rates between pounds, Singapore dollars and Hong Kong dollars are shown below. 1 Singapore dollar = £0.58 £1 = 10.50 Hong Kong dollars Tsion bought a watch in Singapore for 72 Singapore dollars. Ibrahim bought the same model of watch in Hong Kong for 399 Hong Kong dollars. What is the difference between the amounts that Tsion and Ibrahim paid for their watches? Give your answer in pounds.
Answers
The Difference in the amounts that Tsion and Ibrahim paid for their watches is £3.85.
To find the difference in the amounts that Tsion and Ibrahim paid for their watches, we need to convert the prices to the same currency. We can use the exchange rates given to convert both prices to pounds.
1 Singapore dollar = £0.58
72 Singapore dollars = 72 x £0.58 = £41.76
1 Hong Kong dollar = £0.09
399 Hong Kong dollars = 399 x £0.095 = £37.91
Therefore, Tsion paid £41.76 for the watch and Ibrahim paid £37.91 for the same model of watch.
To find the difference in the amounts paid, we can subtract the smaller amount from the larger amount:
£41.76 - £37.91 = £3.85
Therefore, the difference in the amounts that Tsion and Ibrahim paid for their watches is £3.85.
To know more about Difference in the amounts.
https://brainly.com/question/17301989
#SPJ11
Geometry pls help me need help

Answers
suppose where y is a binary random variable. suppose further that eu 0 and 0 < var[x]< oo (a) what is e yx]? what is pty 1x?
Answers
if Y=1+X+u, where X, Y, and u=v+X are random variables, v is independent of X; E(v)=0, Var(v)=1, E(X)=1, and Var(X)=2, then Var(Y|X) = Var ( 1 + X + u | X) = 0 + 4*2 + 1 = 8 + 1 = 9
if Y=1+X+u, where X, Y, and u=v+X are random variables, v is independent of X; E(v)=0, Var(v)=1, E(X)=1, and Var(X)=2, the variance of the following cases are calculated as:
Var(u|X=1) = Var( v + X | X = 1) = Var( v + 1 )
= Var(v) + Var(1)
= 1 + 0 = 1
Var(Y|X=1) = Var( 1 + X + u | X = 1 )
= Var (1 + X + v + X|X=1)
= Var(1 + 1 + v + 1)
= Var(3) + Var(v)
= 0 + 1 = 1
Var(u|X) = Var ( v + X | X)
= Var ( v + X)
= Var(v) + Var(X)
= 1 + 2 = 3
Var(Y|X) = Var ( 1 + X + u | X)
= Var ( 1 + X + v + X | X)
= Var ( 1 + 2X + v)
= Var(1) + Var(2X) + Var(v)
= 0 + 4*2 + 1 = 8 + 1 = 9
learn more about of variable here
https://brainly.com/question/14494614
#SPJ4
Find percent decrease from 9 to 8
Answers
Answer:
Percentage Calculator: What is the percentage increase/decrease from 8. to 9.5? = 18.75.
Given the function f(x) = 3x + 1, evaluate f(a + 1).

Answers
Answer:
3a + 4Step-by-step explanation:
Given the function
f(x) = 3x + 1,Substitute x with a + 1
f(a + 1) = 3(a+1) + 1 = 3a + 3 + 1 = 3a + 4Function
ff(x)=f(x+1), given f(1)=0
Find f(0)
Answers
The value of f(0) in the function is 0.
What is the value of f(0) in the function?
To find f(0), in the given function we can use the given equation:
ff(x) = f(x+1)
Substituting x = 0, we get:
ff(0) = f(1)
Since we are given that f(1) = 0, we have:
ff(0) = 0
Now we can substitute x = -1 into the original equation:
ff(x) = f(x+1)
to get:
ff(-1) = f(0)
Since we know that ff(x) = 0 (from ff(0) = 0), we have:
f(0) = ff(-1) = 0
Therefore, we have found that f(0) = 0.
Learn more about functions here: https://brainly.com/question/25638609
#SPJ1
Solve the homogeneous second-order initial value problem: a) y" + 2y' + 5y = 0,y (0) = 3,y'(0) = 5 b) y" + 6y' +9y = 0, y(0) = 2, y' (0) = 3
Answers
The particular solution that satisfies the initial conditions is:
y(x) =\(3e^(-x)cos(2x) + 8e^(-x)sin(2x)\)
To solve the homogeneous second-order initial value problem y" + 2y' + 5y = 0, with initial conditions y(0) = 3 and y'(0) = 5, we can assume a solution of the form y(x) = e^(rx), where r is a constant to be determined.
Plugging this assumed solution into the differential equation, we get:
y" + 2y' + 5y = 0
\((e^(rx))" + 2(e^(rx))' + 5e^(rx) = 0\)
Differentiating, we have:
\(r^2e^(rx) + 2re^(rx) + 5e^(rx) = 0\)
Factoring out e^(rx), we get:
\((e^(rx))(r^2 + 2r + 5) = 0\)
For this equation to hold for all x, the factor\((r^2 + 2r + 5)\)must be zero:
\(r^2 + 2r + 5 = 0\)
Using the quadratic formula, we find:
r =\((-2 ± sqrt(2^2 - 4(1)(5))) / (2(1))\)
r = (-2 ± sqrt(-16)) / 2
r = (-2 ± 4i) / 2
r = -1 ± 2i
Therefore, the general solution of the homogeneous differential equation is:
y(x) =\(C1e^((-1+2i)x) + C2e^((-1-2i)x)\)
Using Euler's formula e^(ix) = cos(x) + i*sin(x), we can rewrite the solution as:
y(x) = \(C1e^(-x)cos(2x) + C2e^(-x)sin(2x)\)
To find the particular solution that satisfies the initial conditions, we substitute the values of y(0) = 3 and y'(0) = 5 into the general solution and solve for C1 and C2.
y(0) = \(C1e^(-0)cos(20) + C2e^(-0)sin(20) = C1\)
C1 = 3
y'(x) = \(-C1e^(-x)cos(2x) + C1e^(-x)(-sin(2x)) + C2e^(-x)cos(2x) + C2e^(-x)sin(2x)\)
y'(0) = -\(C1e^(-0)cos(20) + C1e^(-0)(-sin(20)) + C2e^(-0)cos(20) + C2e^(-0)sin(20) = -C1 + C2\)
-3 + C2 = 5
C2 = 8
Therefore, the particular solution that satisfies the initial conditions is:
y(x) =\(3e^(-x)cos(2x) + 8e^(-x)sin(2x)\)
b) To solve the homogeneous second-order initial value problem y" + 6y' + 9y = 0, with initial conditions y(0) = 2 and y'(0) = 3, we can follow a similar procedure.
Assuming a solution of the form y(x) = e^(rx), we plug it into the differential equation:
\((e^(rx))" + 6(e^(rx))' + 9e^(rx) = 0\)
Simplifying, we get:
\(r^2e^(rx) + 6re^(rx) + 9e^(rx) = 0\)
Factoring out e^(rx), we have:
\((e^(rx))(r^2 + 6r + 9) = 0\)
For this equation to hold for all x, the factor (r^2 + 6r + 9) must be zero:
(r + 3)^2 = 0
This gives us a repeated root at r = -3.
The general solution of the homogeneous differential equation is:
y(x) =\((C1 + C2x)e^(-3x)\)
To find the particular solution that satisfies the initial conditions, we substitute the values of y(0) = 2 and y'(0) = 3 into the general solution and solve for C1 and C2.
C1 = 2
\(y'(x) = (C2 - 3C2x)e^(-3x)\\y'(0) = (C2 - 3C2(0))e^(-3*0) = C2\)
C2 = 3
Therefore, the particular solution that satisfies the initial conditions is:
y(x) = \((2 + 3x)e^(-3x)\)
Learn more about quadratic here:
https://brainly.com/question/22364785
#SPJ11
What is the relationship between the points on the line and solutions to the linear equation?
Answers
The relationship between the points on the line and solutions to the linear equation is, the equation has a solution at each point along the line.
In the given question, we have to find the relationship between the points on the line and solutions to the linear equation.
The equation has a solution at each point along the line. This simply means that it is easy to tell whether an ordered pair is a solution to an equation. The ordered pair is a solution to the equation if it lies on the line drawn by the linear equation.
To learn more about linear equation link is here
brainly.com/question/11897796
#SPJ4
The number of cans of soft drinks sold in a machine each week is recorded below, develop forecasts using a three period moving average. 338, 219, 278, 265, 314, 323, 299, 259, 287, 302
Answers
The forecasts using a three-period moving average for the number of cans of soft drinks sold each week are 278.33, 254, 285.67, 300.67, 312, 293.67, 281.67, and 282.67.
Using a three-period moving average, we can calculate the forecasts for the number of cans of soft drinks sold each week based on the given data: 338, 219, 278, 265, 314, 323, 299, 259, 287, 302.
To calculate the forecasts, we take the average of the sales for the current week and the two previous weeks. The moving average is then shifted forward one period for each subsequent forecast.
The calculations are as follows:
Forecast 1: (338 + 219 + 278) / 3 = 278.33
Forecast 2: (219 + 278 + 265) / 3 = 254
Forecast 3: (278 + 265 + 314) / 3 = 285.67
Forecast 4: (265 + 314 + 323) / 3 = 300.67
Forecast 5: (314 + 323 + 299) / 3 = 312
Forecast 6: (323 + 299 + 259) / 3 = 293.67
Forecast 7: (299 + 259 + 287) / 3 = 281.67
Forecast 8: (259 + 287 + 302) / 3 = 282.67
In summary, the forecasts using a three-period moving average for the number of cans of soft drinks sold each week are 278.33, 254, 285.67, 300.67, 312, 293.67, 281.67, and 282.67.
Visit here to learn more about average : https://brainly.com/question/31087305
#SPJ11
Will give brainliest please help
Write the answer in Simplest form for the perimeter of the figure.

Answers
Answer:
54
Step-by-step explanation:
x plus 2.7 is greater than or equal to 9.4
Answers
Answer:
X >= 6.7
Step-by-step explanation:
So first of all, what you need is write out the equation from the given prompt
x + 2.7 >= 9.4
Next, what you really want to do is
Subtract 2.7 both side
x >= 9.4 - 2.7
x >= 6.7
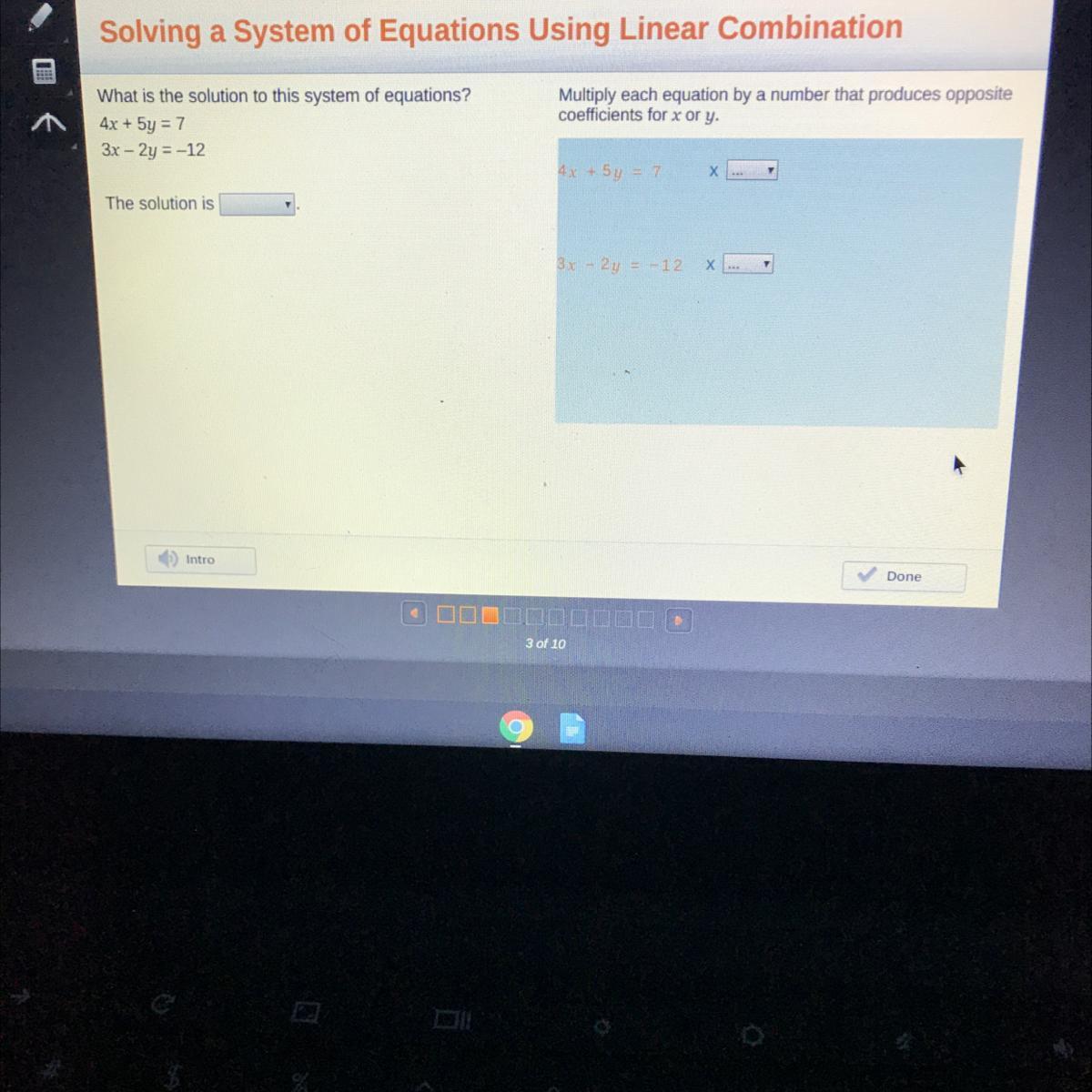
What is the solution to this system of equations?
4x + 5y = 7
3x - 2y = -12
Multiply each equation by a number that produces opposite
coefficients for x ory:
45
The solution is
BN
Answers
Answer:
x = -2, y = 3
Step-by-step explanation:
Given equations are,
4x + 5y = 7 ---------(1)
3x - 2y = -12 ----------(2)
Multiply equation (1) by 3
12x + 15y = 21 ------(3)
Multiply equation (2) by (-4)
-12x + 8y = 48 --------(4)
Now add equations (3) and (4),
(12x + 15y) + (-12x + 8y) = 21 + 48
(12x - 12x) + (15y + 8y) = 69
23y = 69
y = 3
From equation (2),
3x - 2(3) = -12
3x - 6 = -12
3x = 6 - 12
x = -2
Therefore, x = -2 and y = 3 will be the answer.
Answer:
What is the solution to this system of equations?
\(4x +5y = 7\)
\(3x-2y=-12\)
The solution is ✔ \((-2,3)\) .
Use the distance formula to find the distance, to the nearest tenth, from S(6, −2) to V(−4, 3). −5.0 units 3.1 units 11.2 units 8.7 units
Answers
\(~~~~~~~~~~~~\textit{distance between 2 points} \\\\ S(\stackrel{x_1}{6}~,~\stackrel{y_1}{-2})\qquad V(\stackrel{x_2}{-4}~,~\stackrel{y_2}{3})\qquad \qquad d = \sqrt{( x_2- x_1)^2 + ( y_2- y_1)^2} \\\\\\ SV=\sqrt{[-4 - 6]^2 + [3 - (-2)]^2}\implies SV=\sqrt{(-10)^2+(3+2)^2} \\\\\\ SV=\sqrt{125}\implies SV\approx 11.18\implies \underset{\textit{rounded up}}{SV\approx 11.2}\)
Answer:
11.2 units is the answer
Which values for h and k are used to write the function f of x = x squared 12 x 6 in vertex form? h=6, k=36 h=−6, k=−36 h=6, k=30 h=−6, k=−30
Answers
The values for h and k used to write the function f(x) = x² + 12x + 6 in vertex form are h = -6 and k = -9. So the option D is correct.
A vertical parabola's equation in vertex form is equal to
f(x) = a(x - h)² + k
where, (h, k) is the vertex and a is a coefficient.
We have the function:
f(x) = x² + 12x + 6
Now illustrate the function in the form of vertical parabola's equation.
Subtract 6 on both side, we get
f(x) - 6 = x² + 12x
To make x² + 12x as a perfect square we add 36 on both side
f(x) - 6 + 36 = x² + 12x + 36
Now, we can write it as:
f(x) + 30 = (x + 6)²
Subtract 30 on both side, we get
f(x) = (x + 6)² - 30
Now comparing with the equation of vertical parabola
h = -6, k = -30
So the option D is correct.
To learn more about parabola's equation in vertex form link is here
brainly.com/question/29469514
#SPJ4
The complete question is:
Which values for h and k are used to write the function f(x)=x² + 12x + 6 in vertex form?
A. h = 6, k = 36
B. h = −6, k = −36
C. h = 6, k = 30
D h = −6, k = −30
There are 10 students in a class: 7 boys and 3 girls.
If the teacher nicks a group of 4 at random, what is the probability that everyone in the group is a boy?
Answers
Answer:
Total number of students = 10
Probability that all 4 in the group are boys =
\( \frac{4}{10} \\ = 0.4\)
PLEASE HELP ME I WILL MARK U AS THE BRAINIEST ANSWER IF U HELP ME

Answers
Answer:
1st, 3rd
and 4th - "4th" from different answer :)
Step-by-step explanation:
Have a good day :)
Answer:
1,3 and 4
Step-by-step explanation:
After a rainy spring, beavers build a dam that stretches 235 feet across and is 3 feet tall. around the bend, the river is narrower, so a second beaver dam spans 115 feet across. if the proportions of the two dams are the same, how tall is the second dam?
Answers
Answer:
well,
Step-by-step explanation:
as you see.....uhhh.....hmmmm.....if you first a _________________________________
Help me or Shrek's donkey won't get pancakes!

Answers
Answer:
A. y=x and y=x+2
Step-by-step explanation:
A.
y=x and y=x+2
The equations both match the slope and intercept of the graphed equations.
Can I have the pancakes instead of the donkey?