Answers
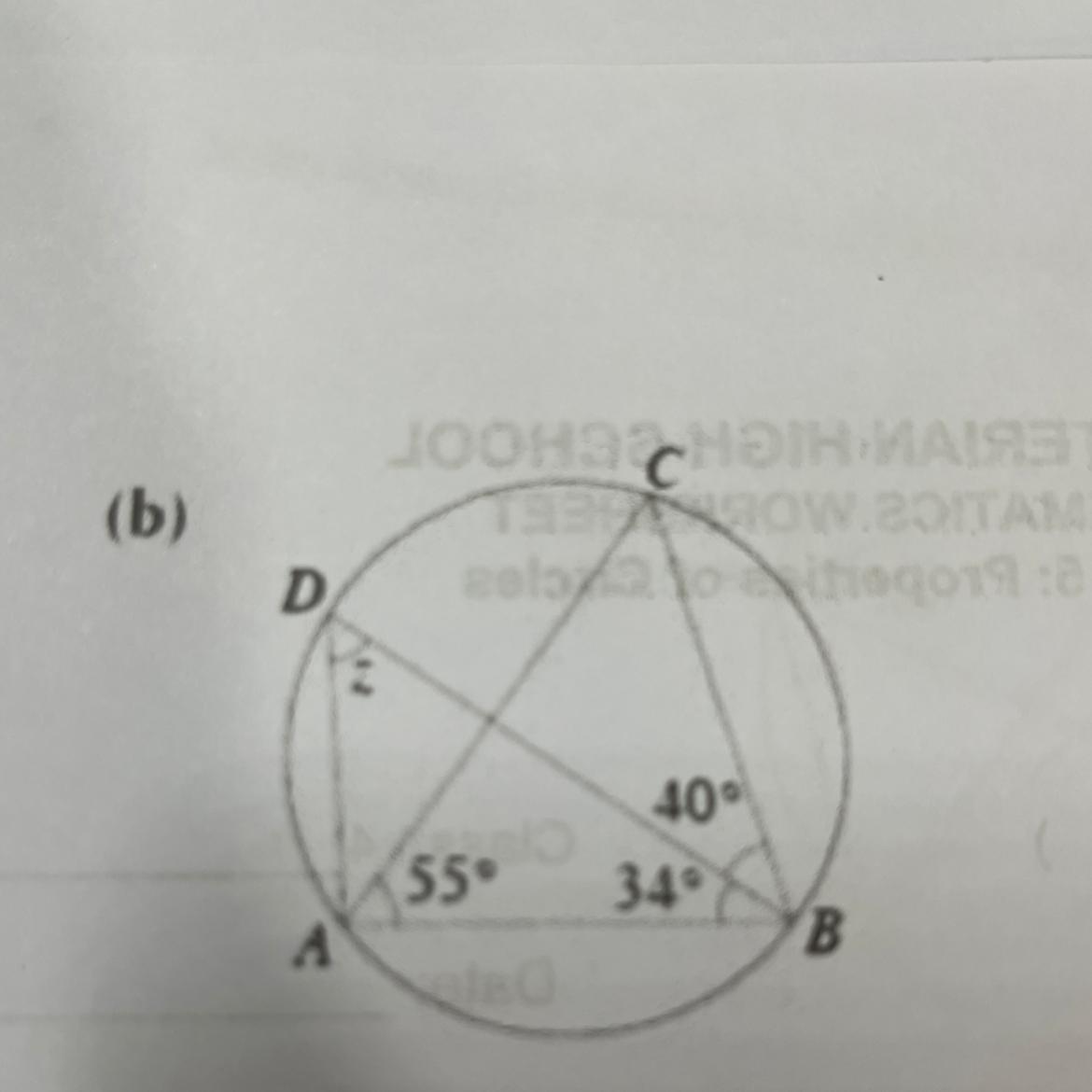
The measure of the angle z of triangle ∆ABD in the same segment with angle C of triangle ∆ABC is equal to 51°
How to evaluate for the angle zWhen two angles are in the same segment, they have the same measure. This means that if you know the measure of one angle in a particular segment, you can determine the measure of any other angle in that segment.
angle z = angle C
angle C = 180° - (55 + 34 + 40)° {sum of interior angles of triangle ABC
angle C = 180° - 129°
angle C = 51°
also;
angle z = 51°
Therefore, the measure of the angle z of triangle ∆ABD in the same segment with angle C of triangle ∆ABC is equal to 51°
Read more about angle here:https://brainly.com/question/24423151
#SPJ1
Related Questions
How to find the width of a rectangle if it's missing
A=21
L=7
W= ?
Answers
Answer:
The width is 3
Step-by-step explanation:
the formula is l×w
How can I find missing angles measurements ? in complementary angles

Answers
If two angles are complementary, it means that their sum is 90 degrees. This means that
angle FGJ + angle JGH = 90
From the diagram, angle JGH = 24.4
Thus,
angle FGJ + 24.4 = 90
angle FGJ = 90 - 24.4
angle FGJ = 65.6 degrees
A 2-column table with 10 rows. The first column is labeled x with entries negative 4, negative 3, negative 2, negative 1, 0, 1, 2, 3, 4, 5. The second column is labeled f of x with entries 105, 0, negative 15, 0, 9, 0, negative 15, 0, 105, 384.
According to the table, which ordered pair is a local minimum of the function, f(x)?
(0, 9)
(4, 105)
(–1, 0)
(2, –15)
Answers
Answer:
option 4 (2,-15)
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
Ken have 9 1/2 cookies. Ken have to split the cookies evenly among 20 people. How much does each person get? [ PLEASE HELP WITH EXPLANATION :D ]
Answers
Answer:
9 1/2 ÷20
9/1 +1/2 ÷20 ( convert to an improper frqction)
18/2 + 1/2 ÷20 ( Multiply 9/1 by 2/2)
19/2 ÷20 ( add 18/2 and 1/2)
19/2 ×1/20 (dividing by 20 is the same as multiplying by 1/20)
19/40
0.475
14. Suppose a math class contains 35 students, 17 females (five of whom speak French) and 18 males (three of whom speak French). Compute the probability that a randomly selected student speaks French, given that the student is male.
Answers
The formula to calculate the conditional probability of A given B is given to be:
\(P(A|B)=\frac{P(A\cap B)}{P(B)}\)If French is represented by F, and males by M, the formula to calculate the probability of a student speaking French given they are male is given to be:
\(P(F|M)=\frac{P(F\cap M)}{P(M)}\)The probability formula is given to be:
\(P(A)=\frac{n(A)}{n(T)}\)Therefore, we have:
\(\begin{gathered} P(F\cap M)=\frac{n(F\cap M)}{n(Students)} \\ n(F\cap M)=students\text{ that speak french and are male}=3 \\ n(Students)=35 \\ \therefore \\ P(F\cap M)=\frac{3}{35} \end{gathered}\)and
\(P(M)=\frac{18}{35}\)Therefore, the conditional probability is:
\(\begin{gathered} P(F|M)=\frac{\frac{3}{35}}{\frac{18}{35}}=\frac{3}{35}\times\frac{35}{18} \\ P(F|M)=\frac{3}{18}=\frac{1}{6}=0.167 \end{gathered}\)The probability is 0.167 or 1/6
b) through (2,9) and parallel to y = 3x - 2
Answers
Answer:
y = 3x+3
aaaaaaa
aaaaaaa
( x , y )
Y = 3x -2
M is 3
Y = mx+c
Y = 3(2) + c
Y = 6 + c
9 = 6 + c
9 - 6 = c
3 = c
So , Y = 3x + 3
Write the formula for the derivative of the function. h(x)=19x 3
−8 x
(Hint: Rewrite x
=x 1/2
) h ′
(x)=
Answers
The derivative of the function h(x) = 19x^(3/2) - 8x is h'(x) = 57x^(1/2) - 8.
To find the derivative of the function h(x) = 19x^(3/2) - 8x, we can use the power rule and the constant multiple rule. First, let's rewrite the function by substituting x^(1/2) for x:
h(x) = 19(x^(1/2))^3 - 8(x^(1/2)
Now, applying the power rule, we have:
h'(x) = 19 * 3(x^(1/2))^(3-1) - 8 * 1(x^(1/2))^(1-1)
h'(x) = 57x^(1/2) - 8(x^(0))
Since x^(0) is equal to 1 for any nonzero x, we have:
h'(x) = 57x^(1/2) - 8(1)
h'(x) = 57x^(1/2) - 8
Learn more about derivative here:
https://brainly.com/question/32963989
#SPJ11
The derivative of the function h(x) = 19x^3 - 8√x is h'(x) = 57x^2 - 4√(x). To find the derivative of the function h(x) = 19x^3 - 8√x, we can apply the power rule and chain rule of differentiation.
First, let's rewrite the function as h(x) = 19x^3 - 8x^(1/2).
To differentiate this function, we need to apply the power rule and chain rule. The power rule states that the derivative of x^n with respect to x is nx^(n-1).
Using the power rule, we differentiate each term of the function separately:
h'(x) = d/dx (19x^3) - d/dx (8x^(1/2))
For the first term, the power rule gives us:
d/dx (19x^3) = 3 * 19x^(3-1) = 57x^2
For the second term, we need to use the chain rule. The chain rule states that if we have a composite function, such as f(g(x)), the derivative is given by f'(g(x)) * g'(x).
In our case, the function is f(x) = -8x^(1/2), and g(x) = x. The derivative of f(x) with respect to g(x) is f'(g(x)) = -4√(x), and the derivative of g(x) with respect to x is 1.
Applying the chain rule, we have:
d/dx (8x^(1/2)) = -4√(x) * 1 = -4√(x)
Now we can substitute the derivatives back into the original expression:
h'(x) = 57x^2 - 4√(x)
Therefore, the derivative of the function h(x) = 19x^3 - 8√x is h'(x) = 57x^2 - 4√(x).
Learn more about functions here:
brainly.com/question/30721594
#SPJ11
A mathematician is wondering what would happen to the surface area of a square if you were to repeatedly cut the square in half. She concludes that the surface area would become less and less but would never become zero units\(^2\). Which equation would help her model the surface area of a square piece of paper as it was repeatedly cut?
a) \(y=x^2+4x-16\)
b) \(y=-25x^2\)
c) \(y=9(2)^x\)
d) \(y=36(\frac{1}{2})^x\)
Answers
The equation that would help the mathematician model the surface area of a square piece of paper as it was repeatedly cut is \(y = 36 \times \frac{1}{2}^x\)
Option D is the correct answer.
We have,
In this equation, the variable x represents the number of times the square is cut in half, and y represents the surface area of the square.
As x increases, the exponent of 1/2 decreases, causing the value of y to decrease.
This exponential decay accurately represents the idea that the surface area becomes less and less but never reaches zero units²
Thus,
The equation that would help the mathematician model the surface area of a square piece of paper as it was repeatedly cut is \(y = 36 \times \frac{1}{2}^x\).
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
The correct equation that would help model the surface area of a square piece of paper as it is repeatedly cut in half is: \(\(y=36(\frac{1}{2})^x\)\)
As the square is cut in half, the side length of the square is divided by 2, resulting in the area being divided by \(\(2^2 = 4\)\).
Therefore, the equation \(y=36(\frac{1}{2})^x\)\)accurately represents the decreasing surface area of the square as it is repeatedly cut in half.
and, \(\(y=x^2+4x-16\)\)is a quadratic equation that does not represent the decreasing nature of the surface area.
and, \(\(y=-25x^2\)\) is a quadratic equation with a negative coefficient.
and, \(\(y=9(2)^x\)\)represents exponential growth rather than the decreasing nature of the surface area when the square is cut in half.
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ1
Find any vertical or slant asymptotes. Consider the following.
f(x) = x^3/ (x² - 49)
Answers
The function \(f(x) = x^3 / (x^2 - 49)\)has a vertical asymptote at x = 7 and x = -7. There are no slant asymptotes. To find the vertical asymptotes of the function f(x), we need to identify the values of x for which the denominator becomes zero, as division by zero is undefined.
In this case, the denominator is (x² - 49). To determine when it equals zero, we set it equal to zero and solve for x:
x² - 49 = 0
This equation can be factored as the difference of squares:
(x - 7)(x + 7) = 0
Setting each factor equal to zero, we find that x = 7 and x = -7. Therefore, the function has vertical asymptotes at x = 7 and x = -7.
On the other hand, to determine if there are any slant asymptotes, we need to check if the degree of the numerator (x³) is greater than the degree of the denominator \((x^2 - 49)\). In this case, the degree of the numerator is 3, while the degree of the denominator is 2. Since the degree of the numerator is greater, there are no slant asymptotes for this function.
In summary, the function \(f(x) = x^3 / (x^2 - 49)\) has vertical asymptotes at x = 7 and x = -7. There are no slant asymptotes.
Learn more about denominator here: https://brainly.com/question/15007690
#SPJ11
Look at the picture below. Do the diagonals bisect each other?
A) Yes
B) No

Answers
Answer:
Yes
Step-by-step explanation:
Since the lines cross over each other, yes, they do bisect each other.
~theLocoCoco
Question 4 Use back-substitution to solve the system of linear equations. 2x+3y-3z = -4 -8y-7z = 73 Z = -7 The solutions are: X= Y = Z = -7
Answers
The solution to the system of linear equations is:x = -18, y = -3, z = -7
The method of back-substitution is used to solve a system of linear equations. This method can be used to calculate the values of one variable at a time. In this method, the variable with the highest power is calculated first, and the values of other variables are calculated by substituting the already calculated variables' values. The method of back-substitution is a straightforward method of solving linear equations, and it is an essential tool for solving more complicated equations, such as those found in engineering, physics, and economics. Back-substitution can be used to solve any linear equation system, whether it is a homogeneous or non-homogeneous system.
To solve the given system of linear equations using back-substitution, we are required to find the values of x and y.
2x+3y-3z = -4-8y-7z = 73
Z = -7
Substituting the value of z = -7 in equation 2, we get:
-8y-7(-7) = 73
-8y + 49 = 73
-8y = 73 - 49
-8y = 24
y = -3
Substituting y = -3 in equation 1, we get:
2x + 3(-3) - 3(-7) = -4
Simplifying: 2x - 9 + 21 = -42
x + 12 = -42
x = -42 - 12
x = -18
Hence, the solution to the system of linear equations is:
x = -18
y = -3
z = -7
Learn more about back-substitution visit:
brainly.com/question/17053426
#SPJ11
A taxi leaves an airport and travels 15 miles east to
drop off a passenger. The taxi driver then has to go
to a point that is 35 miles west of the airport to
drop off his second passenger. He then returns to
the airport to pick up his next fare. How many
miles did he drive?

Answers
Answer:
70 miles
Step-by-step explanation:
15 + 35 + (35 - 15) = 15 + 35 + 20 = 70
A TREE CAST A SHADOW 76 FT LONG. THE ANGLE OF ELEVATION OF THE SUN IS 49 DEGREE, FIND THE HEIGHT OF THE TREES.
1.The height of the tree is what side? (opposite, Adjacent,hypotenuse)
2.Which trig identity will you use to find the height of the tree.
3.The heigh of the tree =

Answers
Answer:
OppositeTangent87.4 ftStep-by-step explanation:
Let the height be x
1. It is the opposite side
2. The ratio of the opposite side to the adjacent side is called the tangent
3. As per definition of the tangent we got:
x/76 = tan 49x = 76*tan 49x = 76*1.15x = 87.4 ftPlease help me with this I do not understand. I did the steps but am really looking for the answer if you could help.

Answers
ANSWER :
The zeros are 1/2 and -5
EXPLANATION :
From the problem, we have the function :
\(f(x)=2x^2+9x-5\)The zeros of the function are the values of x when f(x) = 0
\(2x^2+9x-5=0\)Using quadratic formula with a = 2, b = 9 and c = -5
\(\begin{gathered} x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\ \\ x=\frac{-9\pm\sqrt{9^2-4(2)(-5)}}{2(2)} \\ \\ x=\frac{-9\pm\sqrt{81+40}}{4} \\ \\ x=\frac{-9\pm\sqrt{121}}{4} \\ \\ x=\frac{-9\pm11}{4} \\ \\ x=\frac{-9+11}{4}=\frac{1}{2} \\ \\ x=\frac{-9-11}{4}=-5 \end{gathered}\)
Let \( \vec{A}=5 \hat{i}-2 \hat{j}, \vec{B}=-3 \hat{i}+4 \hat{j} \), and \( \vec{F}=2 \vec{A}-4 \vec{B} \). What is the magnitude of \( \vec{F} \) ? (Chap 3 Prob. 16a)
Answers
The magnitude of vector F is 29.73.\(\( \vec{A}=5 \hat{i}-2 \hat{j}, \vec{B}=-3 \hat{i}+4 \hat{j} \),\) and\(\( \vec{F}=2 \vec{A}-4 \vec{B} \).\)
We need to find the magnitude of \(\( \vec{F} \)\).The magnitude of a vector is defined as the square root of the sum of squares of its components.
It can be mathematically represented as
,\(\[\left | \vec{A} \right | = \sqrt{\vec{A}\cdot \vec{A}}\]\)
Using this formula, we can find the magnitude of vector F as
\(,\[\vec{F}=2 \vec{A}-4 \vec{B} \]\[\vec{F}=2 (5 \hat{i}-2 \hat{j})-4 (-3 \hat{i}+4 \hat{j})\]\[\vec{F}=10\hat{i}-4\hat{j}+12\hat{i}-16\hat{j}\]\[\vec{F}=22\hat{i}-20\hat{j}\]\)
The magnitude of the vector F is
,\(\[\left | \vec{F} \right | = \sqrt{\vec{F}\cdot \vec{F}}\]\[\left | \vec{F} \right | = \sqrt{(22\hat{i})^2+(-20\hat{j})^2}\]\[\left | \vec{F} \right | = \sqrt{484+400}\]\[\left | \vec{F} \right | = \sqrt{884}\]\[\left | \vec{F} \right | = 29.73\]\)
Therefore, the magnitude of vector F is 29.73.
To know more about square root visit:-
https://brainly.com/question/29286039
#SPJ11
A block weighing 90lb rests on a 35 incline. Find the magnitude of the components of the block's weight perpendicular and parallel to the incline.
Find the magnitude perpendicular to the incline.
Find the magnitude parallel to the incline
Answers
A block weighing 90lb rests on a 35° incline. Find the magnitude of the components of the block's weight perpendicular and parallel to the incline.
Solution:
Here, the given data is:
Weight of the block = 90 lb
The angle of incline = 35°
We need to find the following:
Perpendicular component Parallel component
First, let us draw a diagram of the given scenario:
From the above diagram, we can see that the weight of the block is acting in a direction perpendicular to the incline and a direction parallel to the incline.
Hence, we will consider the given angle of 35° as our reference angle for all calculations.
Let W be the weight of the block.
Then,
W sin θ gives the perpendicular component of the weight.
W cos θ gives the parallel component of the weight.
Using the given data, we get:
W = 90 lbθ = 35°
Perpendicular component,
W sin θ= W sin 35°= 90 lb x sin 35°= 51.83 lb (approx)Therefore, the magnitude of the component of the block's weight perpendicular to the incline is 51.83 lb (approx).
Parallel component,
W cos θ= W cos 35°= 90 lb x cos 35°= 73.39 lb (approx)Therefore, the magnitude of the component of the block's weight parallel to the incline is 73.39 lb (approx).
Hence, we get the following results:
Perpendicular component = 51.83 lb (approx)Parallel component = 73.39 lb (approx)
To know more about perpendicular visit :
https://brainly.com/question/12746252
#SPJ11
Prove each of the following statements using strong induction. a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps. b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps. c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Answers
a) By strong induction, any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
b) By strong induction, any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
c) By strong induction, any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
Base case: For postage worth 8 cents, we can use two 4-cent stamps, which can be made using a combination of one 3-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 8, can be made from 3-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 8, we can use the induction hypothesis to make k cents using 3-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with a 5-cent stamp to get the same value. If the last stamp we added was a 5-cent stamp, we can replace it with two 3-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3-cent or 5-cent stamps.
b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
Base case: For postage worth 24 cents, we can use three 8-cent stamps, which can be made using a combination of one 7-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 24, can be made from 7-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 24, we can use the induction hypothesis to make k cents using 7-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 5-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with three 5-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 7-cent or 5-cent stamps.
c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Base case: For postage worth 12 cents, we can use one 3-cent stamp and three 3-cent stamps, which can be made using a combination of two 7-cent stamps.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 12, can be made from 3-cent or 7-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 12, we can use the induction hypothesis to make k cents using 3-cent or 7-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with one 3-cent stamp and two 7-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3
Learn more about strong induction
brainly.com/question/30692296
#SPJ4
Determine the perfect cube whole number closest to 205 632
Answers
Answer: 205,209
Step-by-step explanation:
We want to find a perfect cube that is closest to the number N = 205,632
A perfect cube number is a number such that the square root is a whole number.
Now, to search this number we must take the square root of N:
n = √(205,632) = 453.47
Now, we can round it down or up and get whole numbers, and the squares of those whole numbers will be perfect squares that are near 205,632, lets start with rounding down.
n = 453
the square of 453 is:
453^2 = 205,209
If instead we round up the 453,47, we would get:
n = 454
and the square will be
n = 454^2 = 206,116
Now, to see which one is closser to N, we can take the differences:
205,632 - 205,209 = 423
206,116 - 205,632 = 484
so if we take n = 453 we are closser no N, then the perfect square that is closest to 205,632 is 205,209
Which number line correctly represents the irrational numbers listed below
√18 , π , -√20 , √8 , -√6

Answers
Answer:
D
Step-by-step explanation:
bc it starts with -square root of 20 and then - square root of 6 and the 3.14 and then square root of 8 and then square root of 18
QUICKKK!!!! The membership fee for joining a local indoor trampoline park is $24 per year. The trampoline park charges members of the park $3 for admission to the park. Nonmembers of the trampoline park are charged $6. After how many visits to the trampoline park is the total cost for members, including the membership fee, the same as the total cost for nonmembers?
Answers
Answer:
8 visits
Step-by-step explanation:
Chantal decides to let you choose the slope for the zip line. Choose a slope
that is within the constraints.
Using that slope, how much higher is the starting point of the zip line going to need to be than the ending point?
Enter the difference, in feet, between the heights of the starting and ending
points.
Each tree is 40 feet tall. The trees are 130 feet apart. The slope of the zip line should be 6 to 8 feet of vertical change for every 100 feet of horizontal change. The zip line should have a 5% slack in it. The cable must be high enough that the rider does not touch the ground. The harness hangs down 4 feet below the cable. An additional 3 feet must be used to allow for a riders legs. A brake must be placed on cable. The length of the bungee cord is 16 feet. The bungee cord stretches to a maximum of 175% of its original length.
Answers
The height of the starting point needs to be about 25.76 feet higher than the height of the ending point.
We have,
To find the slope, we can use the given ratio of vertical change to horizontal change:
slope = 6/100 x 130/2 = 4.68
Since the slope is less than 8/100, it is within the constraints.
To find the height difference between the starting and ending points, we need to consider several factors.
First, we need to add the height of the rider, the harness, and the brake above the cable to the height of the cable above the ground:
= 4 + 3 + 16/175 x 16
= 7.74 feet
Next, we need to add the 5% slack in the cable:
= 7.74 + 0.05 x 130
= 14.24 feet
Finally, we need to add the height of the starting tree and subtract the height of the ending tree:
= 40 - 14.24
= 25.76 feet
Therefore,
The height of the starting point needs to be about 25.76 feet higher than the height of the ending point.
Learn more about slope here:
https://brainly.com/question/3605446
#SPJ1
Vilma wants to have P350,000 at the end of 5 years by making a regular deposit at the end of each quarter in an account th pays 9.6% interest, compounded every 3 months. a. Find the amount of quarterly deposit. P b. Find the accumulated amount in the account after the 15 th deposit. rho
Answers
a. The amount of the quarterly deposit is approximately $5,573.39.
b. The accumulated amount in the account after the 15th deposit is approximately $128,523.79.
a. To find the amount of the quarterly deposit, we can use the formula for the future value of an ordinary annuity. The formula is:
A = P * ((1 + r)^n - 1) / r
Where:
A = Accumulated amount
P = Quarterly deposit
r = Interest rate per compounding period
n = Number of compounding periods
In this case, the interest is compounded every 3 months, so the interest rate per compounding period is 9.6% / 4 = 2.4%.
a. To find the quarterly deposit, we need to solve the formula for P. Rearranging the formula, we have:
P = A * r / ((1 + r)^n - 1)
Substituting the given values:
A = $350,000 (the desired accumulated amount)
r = 2.4% (0.024 as a decimal)
n = 5 years * 4 quarters per year = 20 quarters
P = $350,000 * 0.024 / ((1 + 0.024)^20 - 1)
P ≈ $5,573.39
Therefore, the amount of the quarterly deposit is approximately $5,573.39.
b. To find the accumulated amount after the 15th deposit, we can use the future value of an ordinary annuity formula but with a different value for n. Since the interest is compounded every 3 months, the number of compounding periods is 15 quarters.
A = P * ((1 + r)^n - 1) / r
Substituting the given values:
P = $5,573.39 (the calculated quarterly deposit)
r = 2.4% (0.024 as a decimal)
n = 15 quarters
A = $5,573.39 * ((1 + 0.024)^15 - 1) / 0.024
A ≈ $128,523.79
Therefore, the accumulated amount in the account after the 15th deposit is approximately $128,523.79.
Learn more about 'future value of an ordinary annuity':
https://brainly.com/question/25792915
#SPJ11
294y-9)=14 Can anyone solve for y?
Answers
Answer:
y = 4
Step-by-step explanation:
I think you meant
2(4y - 9 ) = 14
Multiply:
2 ×4y = 8y
2× 9 = 18
Thus, we have
8y-18 = 14
Now add 18 to both sides
8y-18+18=14+18
Simplify
8y = 32
Solution:
y = 4
Hence y = 4.
Kavinsky
t(x) = x^3 - 5x^2 - 9x + 45: x - 5
show that binomial is a factor of the polynomial. then factor the polynomial completely.
Answers
Factors of the polynomial are: (x - 3)(x + 3)(x - 5).
What if factoring polynomial?
A polynomial with coefficients in a certain field or in integers is expressed as the product of irreducible factors with coefficients in the same domain by the process of factorization of polynomials, also known as polynomial factorization.
Given:
We have to show tat x - 5 is a factor of the polynomial and to find the factor of the polynomial.
First to show x - 5 is a factor of the given polynomial.
We know that,
If x - 5 is the factor of the given polynomial then by factor theorem x - 5 = 0.
So, x = 5
Plug x = 5 in t(x).
t(5) = 0
That means 5 is the zero of the polynomial t(x).
Therefore, x - 5 is the factor of the polynomial.
Now, to factor the polynomial.
Therefore, after factoring the polynomial we get, .
Answer:
The steps on how to show that the binomial is a factor of the polynomial and then factor the polynomial completely are:
1. Set the binomial equal to 0.
x - 5 = 0
2. Solve for x.
x = 5
3. Substitute the value of x into the polynomial.
t(5) = 5^3 - 5(5^2) - 9(5) + 45
t(5) = 125 - 125 - 45 + 45
t(5) = 0
4. Since the value of the polynomial is 0 when x = 5, the binomial (x - 5) is a factor of the polynomial.
5. To factor the polynomial completely, we can use the difference of squares factorization.
t(x) = (x - 5)(x^2 + 9)
The complete factorization of the polynomial is:
t(x) = (x - 5)(x^2 + 9)
Find the area of the surface given by z = f(x, y) that lies above the region R. f(x, y) = 13 + 4x-3y R: square with vertices (0, 0), (2, 0), (0, 2), (2, 2)
Answers
To find the area of the surface given by z = f(x, y) above the region R, we can integrate the function f(x, y) over the region R. In this case, the function is f(x, y) = 13 + 4x - 3y and the region R is a square with vertices (0, 0), (2, 0), (0, 2), and (2, 2).
To calculate the area, we need to integrate the function f(x, y) over the region R. The integral represents the sum of infinitesimally small areas over the region. In this case, we integrate the function f(x, y) = 13 + 4x - 3y over the square region R.
The integral is given by:
A = ∫∫R f(x, y) dA
where dA represents the infinitesimal area element.
Since R is a square, we can set up the integral using Cartesian coordinates:
A = ∫0^2 ∫0^2 (13 + 4x - 3y) dxdy
Evaluating the integral, we get:
A = ∫0^2 (13x + 2x^2 - 3xy)dy
Simplifying further, we integrate with respect to y:
A = ∫0^2 (13x + 2x^2 - 3xy)dy = (13x + 2x^2 - 3xy) * y |0^2
Substituting the limits of integration, we get:
A = (13x + 2x^2 - 6x) - (0) = 13x + 2x^2 - 6x
Simplifying the expression, we have:
A = 2x^2 + 7x
Therefore, the area of the surface above the region R is given by the function A = 2x^2 + 7x.
Learn more about integrate here
https://brainly.com/question/31744185
#SPJ11
Find the nonzero value() of k that will caue the equation to have the given number and type of olution. Kx2−2x4=0, 2 real olution
Answers
The polynomial equation kx^2 - 2x^4 = 0 has no real solutions, for any non-zero value of k.
The equation kx^2 - 2x^4 = 0 has the form of a polynomial equation, where k and x are variables. To find the nonzero value of k that will cause the equation to have 2 real solutions, we need to analyze the roots of the equation.
The roots of the equation are the values of x that make the equation equal to zero. To find the roots, we can set each factor of the polynomial equal to zero and solve for x:
kx^2 = 0 and 2x^4 = 0
The first equation gives us x = 0, which is not a valid solution, because it is not a real number.
The second equation gives us x^4 = 0, then x = 0. But x = 0 is not a valid solution for this equation, as it is not a real number.
Therefore, the polynomial equation kx^2 - 2x^4 = 0 has no real solutions, for any non-zero value of k.
To learn more about polynomials and its roots visit: brainly.com/question/2557258
#SPJ4
10=6+2f
F=
I’m am really confused about this
Answers
Answer:
f = 2
Step-by-step explanation:
10 = 6 + 2f
subtract 6 from both sides
4 = 2f
divide both sides by 2
2 = f
Subtract 6 from both sides then divide by 2

skiing eight people compete in a downhill ski race. assuming that there are no ties, in how many different orders can the skiers finish?
Answers
Eight people skiing downhill in a race can finish in 40,320 different orders.
Calculating probabilities for a set of possibilities keeping in account the order they are in is called permutation (\({n}_P_{r}\)).
If we overlook the order, it becomes a problem of combination (\({n}_C_{r}\)).
Permutation plays an important role in probability problems where the order of the possible outcomes is concerned. It does not allow repetition of outcomes.
Mathematically, permutation can be represented as:
\({n}_P_{r}=\frac{n!}{(n-r)!}\)
where 'n' represents the total objects/values/instances and 'r' represents our selected number of objects/values/instances.
In this case, we have total 8 drivers (n=8) and 8 positions we are selecting i.e. the order skiing people finish in (r=8);
\({n}_P_{r}=\frac{8!}{(8-8)!}=\frac{8!}{0!}=\frac{40320}{1}\)
To learn more about permutation here https://brainly.com/question/1216161
#SPJ4
What’s the answer???

Answers
Answer:
your answer is (B) -2 & -3
What are mathematical formulas placed in software that performs an analysis on a data set?
a. algorithm
b. intelligence
c. analytics fact
Answers
(A) Algorithms are mathematical formulas placed in software that performs an analysis on a data set.
What is an Algorithm?Algorithms are mathematical algorithms that are used in software to analyze data sets. An algorithm is a finite sequence of strict instructions used to solve a class of specialized problems or to execute a computation in mathematics and computer science. Algorithms serve as specifications for calculating and processing data. Algorithms can utilize artificial intelligence to perform automatic deductions and use mathematical and logical checks to reroute code execution down various paths. Alan Turing pioneered the use of human traits as metaphorical descriptors of machines with terminology like "memory," "search," and "stimulus."
Therefore, (A) algorithms are mathematical formulas placed in software that performs an analysis on a data set.
Know more about an Algorithm here:
https://brainly.com/question/13800096
#SPJ4