Store A's profit is modeled by f(x) =2x, and Store B's profit is modeled by g(x) = 83x. Over what interval is Store A's profit greater than Store B's?
Answers
Over (-∞, 0) interval is Store A's profit greater than Store B's.
To determine the interval over which Store A's profit is greater than Store B's, we need to solve the inequality:
f(x) > g(x)
Substituting the given profit functions, we have:
2x > 83x
Simplifying this inequality, we can subtract 83x from both sides:
-81x > 0
Dividing both sides by -81 (and reversing the inequality because we are dividing by a negative number), we get:
x < 0
Therefore, Store A's profit is greater than Store B's for all values of x less than 0. In interval notation, we can write:
(-∞, 0)
So the interval over which Store A's profit is greater than Store B's is the open interval from negative infinity to 0.
Know more about profit here:
https://brainly.com/question/1078746
#SPJ11
Related Questions
An algebraic expression is described as 7 less than the product of 22
and the sum of t and 18. What is the value of this expression when
t = 13?
Answers
Step-by-step explanation:
22×(t + 18) - 7
t = 13
so,
22×(13 + 18) - 7 = 22×31 - 7 = 682 - 7 = 675
What is the directional derivative of f(x, y) = xe³ — y² + lat (5,0) in the direction 47 - 3j? Your Answer: Answer
Answers
the directional derivative of f(x, y) = xe³ - y² at the point (5, 0) in the direction of the vector 47 - 3j is (141e³) / sqrt(2218).
To find the directional derivative of the function f(x, y) = xe³ - y² at the point (5, 0) in the direction of the vector 47 - 3j, we need to compute the dot product of the gradient of f with the unit vector in the given direction.
First, let's find the gradient of f(x, y):
∇f(x, y) = (∂f/∂x, ∂f/∂y)
Taking partial derivatives:
∂f/∂x = (3e³)x
∂f/∂y = -2y
The gradient of f(x, y) is: ∇f(x, y) = (3e³)x - 2y
To calculate the directional derivative, we need the unit vector in the direction of 47 - 3j. The magnitude of the vector 47 - 3j is:
|47 - 3j| = sqrt(47² + (-3)²) = sqrt(2209 + 9) = sqrt(2218)
The unit vector in the direction of 47 - 3j is obtained by dividing the vector by its magnitude:
u = (47 - 3j) / |47 - 3j|
u = (47 - 3j) / sqrt(2218)
Now, we can compute the directional derivative by taking the dot product of the gradient with the unit vector:
Directional derivative = ∇f(x, y) · u
= [(3e³)x - 2y] · [(47 - 3j) / sqrt(2218)]
= (3e³)(47) / sqrt(2218) - (2)(0) / sqrt(2218) [since we are evaluating at (5, 0)]
= (141e³) / sqrt(2218)
To know more about function visit:
brainly.com/question/30721594
#SPJ11
Please help with that

Answers
It takes them 3 hours for a 1.5 meter wall.
So you need to see how many 1.5 are in 9.
I did 9/1.5
Which is 6. And since it takes them 3 hours for each 1.5.
3x6 is
18
The sum of two numbers is 50. If the larger number is divided by the
smaller number we get 7/11. Find the numbers.
Answers
Answer:
Set two equations:
Number #1 = xNumber #2 = y\(\left \{ {{x+y=50} \atop {\frac{x}{y}=\frac{7}{11} }} \right.\)
Rearrange one of the equations to find the value of a variable:
\(x+y=50\\x=50-y\)
Substitute in that value into the other equation:
\(\frac{50-y}{y}=\frac{7}{11}\)
Cross-multiply & solve for y:
\(7y=11(50-y) \\7y=550-11y\\7y+11y=550\\18y=550\\y=\frac{550}{18}=\frac{275}{9}\)
Substitute in the value to the original equation to find x:
\(\frac{x}{\frac{275}{9}}=\frac{7}{11} \\\frac{9x}{275}=\frac{7}{11} \\9(11)x=275(7)\\99x=1925\\x=\frac{1925}{99} =\frac{175}{9}\)
Therefore, the answer will be:
x = \(\frac{175}{9}\)y = \(\frac{275}{9}\)You can check your answers by:
\(\frac{175}{9} +\frac{275}{9} =\frac{450}{9} =50\)
\(\frac{\frac{175}{9} }{\frac{275}{9} } =\frac{175}{9} *\frac{9}{275} =\frac{175}{275}=\frac{7}{11}\)
Answer:
x = 175/9
y = 275/9
Step-by-step explanation:
Let the larger number be 'x' and smaller number be 'y'
sum of two numbers is 50.
x +y = 50 --------(I)
x = 50 - y -------------(II)
The larger number is divided by the smaller number we get 7/11.
\(\frac{x}{y}=\frac{7}{11}\\\\\)
Cross multiply,
11x = 7y
11x - 7y = 0 ------------(III)
Substitute x = 50 -y in equation (III)
11*(50-y) - 7y = 0
11*50 - 11*y - 7y = 0 {Distributive property}
550 - 11y - 7y = 0
550 - 18 y = 0 {Combine like terms}
Subtract 550 from both sides
- 18y = -550
Divide both sides by (-18)
y = -550/-18
y = 275/9
substitute y = 275/9 in equation (III)
\(11x - 7*(\frac{275}{9})=0\\\\11x-\frac{1925}{9}=0\\\\11x =\frac{1925}{9}\\\\x=\frac{1925}{9*11}\\\\x=\frac{175}{9}\)
write a pair of integers whose a)sum-1 b)diffrence is -5
please give the answer only last question in my test
Answers
Answer:
x = -3
y = 2
Step-by-step explanation:
Let the two integers be x and y
sum is -1
x + y = -1 •••(i)
x-y = -5 •••••(ii)
From ii, x = -5 + y
substitute into i
-5 + y+ y = -1
-5 + 2y = -1
2y = -1 + 5
2y = 4
y = 4/2
y = 2
Recall;
x = -5 + y
x = -5 + 2
x = -3
coin $a$ is flipped three times and coin $b$ is flipped four times. what is the probability that the number of heads obtained from flipping the two fair coins is the same?
Answers
The probability that the number of heads obtained from flipping the two fair coins is the same is 35/128.
Probability:
Probability means the fraction of favorable outcome and the total number of outcomes.
So it can be written as,
Probability = Favorable outcomes / Total outcomes
Given,
The coin a is flipped three times and coin b is flipped four times.
Here we need to find the probability that the number of heads obtained from flipping the two fair coins is the same.
We know that,
There are 4 ways that the same number of heads will be obtained;
0, 1, 2, or 3 heads.
The probability of both getting 0 heads is
\($\left(\frac12\right)^3{3\choose0}\left(\frac12\right)^4{4\choose0}=\frac1{128}$\)
Probability of getting 1 head,
\($\left(\frac12\right)^3{3\choose1}\left(\frac12\right)^4{4\choose1}=\frac{12}{128}$\)
Probability of getting 2 heads is,
\($\left(\frac12\right)^3{3\choose2}\left(\frac12\right)^4{4\choose2}=\frac{18}{128}$\)
And the probability of getting 3 heads is,
\($\left(\frac12\right)^3{3\choose3}\left(\frac12\right)^4{4\choose3}=\frac{4}{128}$\)
Therefore, the probability that the number of heads obtained from flipping the two fair coins is the same is,
=> (1/128) + (12/128) + (18/128) + (4/128)
=> 35/128.
To know more about probability here
https://brainly.com/question/14210034
#SPJ4
you need to add lines, segments, and angles to create your ultimate circle. you need to incorporate specific theorems. Each problem must ask for a missing measure(an arc measure, segment length or angle measure. Provide information that someone would need to solve at the top of the puzzle could include angle measures, arc measures, tangent lines, parallel ect. You must list which problem number is used for each listed theorem show all work.

Answers
Some information that someone might use to solve problems related to a circle design is the Tangent Arc theorem.
What is the tangent arc theorem?The tangent arc theorem states that if an angle is formed by two secants, one secant, one tangent, or two tangents, and also intersects in a space outside of the circle, then the value obtained will be equal to the difference of the values of the intercepted arcs divided by one and a half.
Also, note that angles outside a circle are those whose vertex or arc is pointed outwards and their sides are either secants or tangents. With this information, it will be possible to solve problems related to tangent lines and arc measures.
Learn more about the tangent arc theorem here:
https://brainly.com/question/29239907
#SPJ1
Macey is considering the following jobs. She will earn commission at each job based on her estimated sales. How much would her earnings be at Job A?

Answers
9514 1404 393
Answer:
$1320
Step-by-step explanation:
The amount of commission is the product of the commission rate on sales and the amount of sales:
Job A commission = 0.12 × $11,000 = $1320
_____
It may help you to realize that the percent symbol (%) is fully equivalent to /100. That is 12% = 12/100 = 0.12.
26. Alex can complete a certain task in 10 hours. Working together, Alex and Eli can do it in 6 hours. How long will it take Eli alone to complete the task?
Answers
Eli will take 12 hours alone to complete the task.
What are distance word problems?Algebra word problems frequently take the form of distance word problems. They involve a situation in which you must determine the speed, distance, or duration of one or more objects' travels. Because one of the most well-known distance problems involves determining the precise moment when two trains traveling in opposite directions cross paths, these are frequently referred to as "train problems."distance = rate x timed = rtIn other words, the distance you traveled is equal to the time you spent driving multiplied by the speed you were traveling at.Acc to our question-
alex take 10 hrs to complete a workalex and eli both take 6 hours.distance = rate x timed = rtdistance = rate x timeeli will take 4 hrsHence,Eli will take 4 hrs.
learn more about distance word problems click here:
https://brainly.com/question/29030072
#SPJ13
Use the Euclidean algorithm to find ged(707, 413), and find integers s, t such that 707s + 413t = gcd (707,413). (b) Are there integers x, y such that 707x +413y = 9? If there are, give an example. If there are no such r, y, then prove it.
Answers
a) Using the Euclidean algorithm, we can find gcd (707,413) as follows:707 = 1 · 413 + 294413 = 1 · 294 + 119294 = 2 · 119 + 562119 = 2 · 56 + 71356 = 4 · 71 + 12 71 = 5 · 12 + 11 12 = 1 · 11 + 1
Thus, gcd (707,413) = 1.
We can find the coefficients s and t that solve the equation 707s + 413t
= 1 as follows:1 = 12 - 11 = 12 - (71 - 5 · 12) = 6 · 12 - 71 = 6 · (119 - 2 · 56) - 71
= - 12 · 56 + 6 · 119 - 71
= - 12 · 56 + 6 · (294 - 2 · 119) - 71 = 18 · 119 - 12 · 294 - 71
= 18 · 119 - 12 · (413 - 294) - 71 = 30 · 119 - 12 · 413 - 71
= 30 · (707 - 1 · 413) - 12 · 413 - 71 = 30 · 707 - 42 · 413 - 71
Thus, s = 30, t = -42. So we have found that 707(30) + 413(−42) = 1.
b) Since 707s + 413t = 1 and 9 does not divide 1, the equation 707x + 413y = 9 has no integer solutions. Therefore, we can conclude that there are no such integers x and y.
To know more about Euclidean visit :
https://brainly.com/question/3589540
#SPJ11
In ΔRST, s = 93 inches, ∠S=123° and ∠T=28°. Find the length of r, to the nearest 10th of an inch.
Answers
We have been given that in ΔRST, s = 93 inches, ∠S=123° and ∠T=28°. We are asked to find the length of r to the nearest 10th of an inch.
We will use law of sines to solve for side r.
\(\frac{a}{\text{Sin}(a)}=\frac{b}{\text{Sin}(B)}=\frac{c}{\text{Sin}(C)}\), where a, b and c are corresponding sides to angles A, B and C respectively.
Let us find measure of angle S using angle sum property of triangles.
\(\angle R+\angle S+\angle T=180^{\circ}\)
\(\angle R+123^{\circ}+28^{\circ}=180^{\circ}\)
\(\angle R+151^{\circ}=180^{\circ}\)
\(\angle R+151^{\circ}-151^{\circ}=180^{\circ}-151^{\circ}\)
\(\angle R=29^{\circ}\)
\(\frac{r}{\text{sin}(R)}=\frac{s}{\text{sin}(S)}\)
\(\frac{r}{\text{sin}(29^{\circ})}=\frac{93}{\text{sin}(123^{\circ})}\)
\(\frac{r}{\text{sin}(29^{\circ})}\cdot \text{sin}(29^{\circ})=\frac{93}{\text{sin}(123^{\circ})}\cdot \text{sin}(29^{\circ})\)
\(r=\frac{93}{0.838670567945}\cdot (0.484809620246)\)
\(r=110.889786233799179\cdot (0.484809620246)\)
\(r=53.7604351\)
Upon rounding to nearest tenth, we will get:
\(r\approx 53.8\)
Therefore, the length of r is approximately 53.8 inches.
how many ways are there to seat 6 people around a circular table where two sections are considered the same when everyone has the same immediate left and immediate right neighbor?
Answers
There are average 360 ways to seat 6 people around a circular table since any arrangement with the same immediate left and right neighbor is considered the same.
For seating 6 people around a circular table, there are many possible arrangements. However, two arrangements are considered the same if everyone has the same immediate left and right neighbor. This means that, for any given seating arrangement, there are six possible rotations, so the total number of different arrangements is 6 times the number of arrangements that can be made with the initial seating. Since there are 6! (6 factorial, or 6x5x4x3x2x1) arrangements that can be made with the initial seating, the total number of different seating arrangements is 6! x 6, or 360. In other words, there are 360 ways to seat 6 people around a circular table where two sections are considered the same when everyone has the same immediate left and immediate right neighbor.
Learn more about average here
https://brainly.com/question/24057012
#SPJ4
A plastic pool gets filled up with 10L of water per hour.
a) After 2 hours how much water is in the pool? Write an equation.
b) After how many hours will the pool be 80L?
c) Is part b) linear or nonlinear?
Answers
a) The amount of water in the pool after 2 hours can be calculated using the equation.
Water in pool = 10L/hour × 2 hours = 20L.
b) The pool will be 80L when the equation is satisfied: 80L = 10L/hour × Time.
Solving for Time, we find Time = 8 hours.
c) Part b) is linear.
a) To calculate the amount of water in the pool after 2 hours, we can use the equation:
Water in pool = Water filling rate × Time
Since the pool gets filled up with 10L of water per hour, we can substitute the values:
Water in pool = 10 L/hour × 2 hours = 20L
Therefore, after 2 hours, there will be 20 liters of water in the pool.
b) To determine the number of hours it takes for the pool to reach 80 liters, we can set up the equation:
Water in pool = Water filling rate × Time
We want the water in the pool to be 80 liters, so the equation becomes:
80L = 10 L/hour × Time
Dividing both sides by 10 L/hour, we get:
Time = 80L / 10 L/hour = 8 hours
Therefore, it will take 8 hours for the pool to contain 80 liters of water.
c) Part b) is linear.
The equation Water in pool = Water filling rate × Time represents a linear relationship because the amount of water in the pool increases linearly with respect to time.
Each hour, the pool fills up with a constant rate of 10 liters, leading to a proportional increase in the total volume of water in the pool.
For similar question on amount.
https://brainly.com/question/25720319
#SPJ8
The average and standard deviation of the weights of 350 Indian students are 55 kg and 3 kg respectively. And the average and standard deviation of weights of 450 German students are 60 kg and 4 kg respectively. a. Determine the combined mean weight of all those Indian and German students. b. Find the standard deviation of weight for the combined group of students.
Answers
The combined mean weight of all Indian and German students is 57.81 kg. The combined standard deviation of weight for the group is 3.59 kg.
The combined mean weight is calculated by adding the mean weights of the two groups and dividing by the total number of students. In this case, the mean weight of the Indian students is 55 kg and the mean weight of the German students is 60 kg. There are a total of 350 Indian students and 450 German students, so the combined mean weight is (350 * 55 + 450 * 60) / (350 + 450) = 57.81 kg.
The combined standard deviation is calculated using a formula that takes into account the standard deviations of the two groups and the number of students in each group. In this case, the standard deviation of the Indian students is 3 kg and the standard deviation of the German students is 4 kg. The combined standard deviation is sqrt((350 * 3^2 + 450 * 4^2) / (350 + 450)) = 3.59 kg.
Learn more about standard deviation here:
brainly.com/question/29088233
#SPJ11
Please answer now correct answer fast

Answers
Answer:
\( Area = 112.1 m^2 \)
Step-by-step Explanation:
Given:
∆WXY
m < X = 130°
WY = x = 31 mm
m < Y = 26°
Required:
Area of ∆WXY
Solution:
Find the length of XY using Law of Sines
\( \frac{w}{sin(W)} = \frac{x}{sin(X)} \)
X = 130°
x = WY = 31 mm
W = 180 - (130 + 26) = 24°
w = XY = ?
\( \frac{w}{sin(24)} = \frac{31}{sin(130)} \)
Multiply both sides by sin(24) to solve for x
\( \frac{w}{sin(24)}*sin(24) = \frac{31}{sin(130)}*sin(24) \)
\( w = \frac{31*sin(24)}{sin(130)} \)
\( w = 16.5 mm \) (approximated)
\( XY = w = 16.5 mm \)
Find the area of ∆WXY
\( area = \frac{1}{2}*w*x*sin(Y) \)
\( = \frac{1}{2}*16.5*31*sin(26) \)
\( = \frac{16.5*31*sin(26)}{2} \)
\( Area = 112.1 m^2 \) (to nearest tenth).
10 points so Yee, I spam a ton of these cause I don’t pay attention

Answers
The area of the given trapezoid is 27280 cm².
QuadrilateralsThere are different quadrilaterals, for example square, rectangle, rhombus, trapezoid, and parallelogram. Each type is defined accordingly to its length of sides and angles. For example, in a square, all angles are 90° and all sides present the same value.
The sum of the interior angles of a quadrilateral is equal to 360°.
Area of Compound ShapesThis question requires your knowledge about the area of compound shapes. For solving this, you should:
Identify the basic shapes; Calculate your individual areas; Subtract each area found. STEP 1 - Identify the basic shapes.The trapezoid is composed for:
- 2 triangles whose sides are equal to 34 cm and 110 cm/ 22 cm and 110cm.
- 1 rectangle whose sides are 220 cm and 110 cm.
Therefore, you should sum the area of these geometric figures for finding the total area.
STEP 2 - Find the area of the triangles.Area of each triangle = \(\frac{bh}{2}\), where b=the length of the side and h= the height of the triangle. Then,
A_triangle1= \(\frac{bh}{2}=\frac{34*110}{2}\)=1870 cm²
A_triangle2= \(\frac{bh}{2}=\frac{22*110}{2}\)=1210cm²
STEP 3 - Find the area of the rectangle.Area of the rectangle=bh, where b=the length of the side and h= the height of the rectangle. Then,
A_rectangle= bh=110*220=24200
STEP 4 - Find the area of the trapezoidA_trapezoid= A_rectangle+A_triangle1+A_triangle2
A_trapezoid= 24200+1870+1210
A_trapezoid= 27280 cm²
Learn more about the area of compound shapes here:
brainly.com/question/15884960
#SPJ1
This graph represents Malcoms distance from school in meter's t minutes after he leaves his house on his way to schoolwhat does the slope represent in this situation
Answers
What is the answer hurry!!!

Answers
Answer:
D. 9 + 4√5
Step-by-step explanation:
What we're essentially doing here is squaring 2 + √5. (2 + √5 and 2 + 1√5 are essentially the same)
(2 + √5)(2 + √5) (I didn't put the one on the conjugate for a reason; look above)
Step 1: Apply the distributive property by multiplying each term of 2 + √5 by 2 + √5
4 + 2√5 + 2√5 + (√5)²
Step 2: Combine 2√5 and 2√5 to get 4√5.
4 + 4√5 + (√5)²
Step 3: The square of √5 is 5.
4 + 4√5 + 5
Step 4: Add 4 and 5 to get 9.
9 + 4√5 is the final answer to this question.
State whether the variable is discrete or continuous.The number of cars a car dealer sells in a day. The time it takes to have a medical physical exam.
Answers
A discrete variable is a variable whose value is obtained by counting while a continuous variable is a variable whose value is obtained by measuring.
From the question,
The number of cars a car dealer sells in a day is a discrete variable.
The time it takes to have a medical physical exam is a continuous variable.
A scatter plot is shown on the coordinate plane. scatter plot with points at 1 comma 8, 2 comma 6, 4 comma 7, 5 comma 5, 7 comma 6, 8 comma 4, 10 comma 3, and 10 comma 5 Which of the following graphs shows a line on the scatter plot that fits the data? scatter plot with points at 1 comma 8, 2 comma 6, 4 comma 7, 5 comma 5, 7 comma 6, 8 comma 4, 10 comma 3, and 10 comma 5, with a line passing through the coordinates 7 comma 6 and 10 comma 5 scatter plot with points at 1 comma 8, 2 comma 6, 4 comma 7, 5 comma 5, 7 comma 6, 8 comma 4, 10 comma 3, and 10 comma 5, with a line passing through the coordinates 2 comma 6 and 5 comma 5 scatter plot with points at 1 comma 8, 2 comma 6, 4 comma 7, 5 comma 5, 7 comma 6, 8 comma 4, 10 comma 3, and 10 comma 5, with a line passing through the coordinates 2 comma 7 and 7 comma 5 scatter plot with points at 1 comma 8, 2 comma 6, 4 comma 7, 5 comma 5, 7 comma 6, 8 comma 4, 10 comma 3, and 10 comma 5, with a line passing through the coordinates 1 comma 8 and 10 comma 3
Answers
The line passing through the coordinates 7,6 and 10,5 seems to fit the data best, as it passes through several of the points and follows the general trend of the data. Therefore, the graph that shows a line passing through the coordinates 7,6 and 10,5 is the one that fits the data.
So, the correct answer is: scatter plot with points at 1,8; 2,6; 4,7; 5,5; 7,6; 8,4; 10,3; and 10,5, with a line passing through the coordinates 7,6 and 10,5.
........help me........

Answers
Using the formula of volume of rectangular prism;
1. The volume of the rectangular prism is 3672cm³
2. The volume of the rectangular prism is 630in³
3. The volume of the rectangular prism is 3744ft³
What is the volume of the rectangular prism?The volume of a rectangular prism can be calculated by multiplying its length (l), width (w), and height (h). The formula for the volume of a rectangular prism is:
Volume = length × width × height
V = l × w × h
By substituting the given values for the length, width, and height into the formula, you can calculate the volume of the rectangular prism.
1. To find the volume of the rectangular prism, we have to substitute the value into the formula;
v = 9 * 24 * 17
v = 3672cm³
2. The volume of the rectangular prism is given as;
v = 4.5 * 14 * 10
v = 630in³
3. The volume of the rectangular prism is given as;
v = 8 * 12 * 39
v = 3744ft³
Learn more on volume of rectangular prism here;
https://brainly.com/question/23665595
#SPJ1
consists of $1$'s separated by blocks of $2$'s with $n$ $2$'s in the $n^{\rm{th}}$ block. what is the sum of the first $1234$ terms of this sequence?
Answers
Therefore, the sum of the first 1234 terms of this sequence is 1234.
To find the sum of the first 1234 terms of the sequence consisting of 1's separated by blocks of 2's with n 2's in the nth block, we need to determine the number of blocks and the number of 1's in each block.
Let's examine the pattern of the sequence:
Block 1: 2's
= 1's
= 1 (1 2)
Block 2: 2's
= 2's
= 22 (1 22 1)
Block 3: 2's
= 3's
= 222 (1 222 1)
Block 4: 2's
= 4's
= 2222 (1 2222 1)
...
We observe that the number of 2's in each block is equal to the number of the block itself. So, in the nth block, there are n 2's.
Now, let's calculate the number of blocks required to reach the 1234th term:
To find the number of blocks, we need to determine the maximum block number before the 1234th term. We can calculate this by finding the sum of the series 1 + 2 + 3 + ... + n until the sum is greater than or equal to 1234.
The formula for the sum of the series 1 + 2 + 3 + ... + n is given by: S = (n/2)(n+1).
Let's solve this equation:
(n/2)(n+1) = 1234
\(n^2 + n - 2468 = 0\)
Using the quadratic formula:
n = (-1 + √(1 + 4*2468)) / 2
n ≈ 61.76
Since n must be a whole number, we take the ceiling of n, which gives us 62.
Therefore, there are 62 blocks in the sequence.
Next, let's calculate the number of 1's in each block:
In the nth block, there are n 2's. Since each 2 is separated by a 1, there are n + 1 terms in each block.
So, the number of 1's in each block is (n + 1) - n = 1.
Since there is always one 1 between two consecutive blocks, the total number of 1's in the sequence is equal to the number of blocks, which is 62.
Finally, let's calculate the sum of the first 1234 terms:
Each block has n + 1 terms, which gives us (n + 1) + (n + 1) + ... + (n + 1) (62 times).
Sum of (n + 1) repeated 62 times = 62(n + 1)
= 62 * 2
= 124.
In addition to the blocks, we have 1234 - 62 = 1172 remaining terms, which are all 1's.
So, the sum of the first 1234 terms is 62 + 1172 = 1234.
To know more about sequence,
https://brainly.com/question/20707381
#SPJ11
8 ft
6 ft
Find the area of this figure. Round your
answer to the nearest hundredth. Use
3.14 to approximate a.
A = [ ? ] ft?
Notice that only half of the circle is included in the figure!

Answers
The figure contains a triangle and a semicircle
The area of the figure is 49.12 square feet
How to determine the areaThe dimension of the triangle is:
Base = 8 ft
Height = 6ft
So, the area is:
Area = 0.5 * Base * Height
This gives
Area = 0.5 * 8ft * 6ft
Evaluate
Area = 24 square feet
The radius of the semicircle is:
r = 4 ft.
So, the area is:
\(Area = 0.5\pi r^2\)
This gives:
Area = 0.5*3.14 * 4^2
Area = 25.12 square feet
Add the calculated areas.
Total = 24 square feet + 25.12 square feet
Total = 49.12 square feet
Hence, the area of the figure is 49.12 square feet
Read more about area at:
https://brainly.com/question/24487155
what is the expected number of left-handed students in a typical class of 188 students, and with what standard deviation? what is the expected number of right-handed students (out of 188), and with what standard deviation?
Answers
The expected number of left-handed students in a typical class of 188 students can be estimated using the prevalence rate of left-handedness in the general population.
According to studies, approximately 10% of the population is left-handed. Therefore, we can expect around 18.8 left-handed students in a class of 188 students.
To calculate the standard deviation, we need additional information. The standard deviation depends on the variability of left-handedness in the population. Without this data, it is not possible to provide an accurate estimation of the standard deviation.
Similarly, the expected number of right-handed students can be estimated by subtracting the expected number of left-handed students (18.8) from the total number of students (188). This gives us an expected number of around 169.2 right-handed students.
To know more about population visit:-
https://brainly.com/question/15889243
#SPJ11
The zoom feature on a camera lens allows you dilate what appears on the display. When you change from 100% to 200%, the new image on your screen is an enlargement of the previous image with a scale factor of 2. If the new image is 19 millimeters wide, what was the width of the previous image?
Answers
The width of the previous image was 9.5 millimeters.
If the new image is an enlargement of the previous image with a scale factor of 2, it means that the width of the new image is twice the width of the previous image.
Let's denote the width of the previous image as "x" millimeters.
According to the information given, the width of the new image is 19 millimeters.
Since the new image is an enlargement with a scale factor of 2, we can set up the following equation:
\(2x = 19\)
To find the width of the previous image, we need to solve this equation for "x."
Dividing both sides of the equation by 2, we get:
\(x=\frac{19}{2}\)
\(x = 9.5\)
Therefore, the width of the previous image was 9.5 millimeters.
For such more questions on width
https://brainly.com/question/19634537
#SPJ8
NEED HELP ASAP PLEASE WILL GIVE BRAINLIEST
Circle A has radius AB and Circle X has radius XY. Points A and X are distinct points.
Complete the statements below describing how to prove that the circles are similar.
Translate the center of circle A onto point __ __.
Then dilate the image of circle A about its center by a scale factor of __ __.

Answers
This new circle is the dilated image of circle A, and we can see that it is similar to circle X, with a scale factor of XY/AB. Therefore, the two circles are similar.
What is circle?
The eccentricity is 0 and the two foci are coincident in a circle, which is a special type of ellipse. A circle is also known as the location of points that are evenly spaced apart from the centre. The radius of a circle is measured from the centre to the edge.
To prove that the circles are similar, we have to translate the center of circle A onto point X and then dilate the image of circle A about its center by a scale factor of XY/AB. The complete statements below describe how to prove that the circles are similar.
Translation:
First, we will translate the center of circle A to the point X. To do this, we will use a straightedge and draw a line from the center of circle A to point X. Then we will measure the length of this line, and with the same length, we will draw a new line from point X parallel to the original line. This new line intersects the circle A at a new point B′.
Dilation:
Next, we will dilate the image of circle A about its center by a scale factor of XY/AB. To do this, we will use a compass to draw a circle with radius XY centered at point X. Then we will draw a line from the center of circle A to point B′.
This line intersects the circle with radius XY at a new point Y. We will then draw a new circle with center A and radius AY. This new circle is the dilated image of circle A, and we can see that it is similar to circle X, with a scale factor of XY/AB. Therefore, the two circles are similar.
Learn more about circles on:
https://brainly.com/question/22430239
#SPJ1
Problem 2: Find the unit step response, y(t), for the LTI with Transfer Function H(s). H(s)=(s+4)(s+5)′(s+2)X(s)=s1,Y(s)=X(s)H(s)
Answers
The unit step response, y(t), for the given LTI system with transfer function H(s) = (s+4)(s+5)′(s+2), and input X(s) = 1/s, is a function of time that can be represented as \(y(t) = (4/3)e^(-2t) - (4/3)e^(-5t) - (1/3)e^(-4t) + (1/3)e^(-2t)\).
The unit step response of a linear time-invariant (LTI) system represents the output of the system when the input is a unit step function. In this case, the transfer function H(s) is given as (s+4)(s+5)′(s+2), where s is the Laplace variable. The prime symbol (') denotes differentiation with respect to s.
To find the unit step response, we first need to determine the inverse Laplace transform of the transfer function H(s). By applying partial fraction decomposition, the transfer function can be expressed as H(s) = A/s + B/(s+2) + C/(s+4) + D/(s+5), where A, B, C, and D are constants.
Taking the inverse Laplace transform of each term using known transforms, we obtain the time-domain representation of H(s) as \(y(t) = (4/3)e^(-2t) - (4/3)e^(-5t) - (1/3)e^(-4t) + (1/3)e^(-2t)\).
In summary, the unit step response y(t) for the given LTI system is a function of time that includes exponential terms with different coefficients and time constants. This response represents the system's output when the input is a unit step function.
Learn more about transfer function
brainly.com/question/31326455
#SPJ11
Nadia is a stockbroker. She earns 12% commission each week. Last week, she sold $7,200 worth of stocks. How much did she make last week in commission?
Answers
Answer:
864
Step-by-step explanation:
Question:
Nadia is a stockbroker. She earns 12% commission each week. Last week, she sold $7,200 worth of stocks. How much did she make last week in commission?
What were trying to find:
How much did she make last week in commission?
Answer:
Nadia made $44,928 last week.
Step-by-step explanation:
7,200 x 12% = $864 (0.12)
$864 x 52 = $44,928
Therefore, $44,928 is your answer.
Hope this helped! :^)
⭐Brainliest will be appreciated!⭐
✉️Message me if you have any more questions!✉️
- ✨7272033Alt✨
Submitted on 4/18/2022 at 12:06 PM
(To avoid plagarism, by users whom decide to copy.)
At a hospital, 56 percent of the babies born are not girls. of the baby girls born, 12 percent are premature. what is the probability of a premature baby girl being born at this hospital? round to the nearest percent.5%7!'%
Answers
The probability of a premature baby girl being born at this hospital is 5%.
Let's break down the problem step by step. We are given that 56% of the babies born are not girls. This implies that the remaining 100% - 56% = 44% of the babies born are girls.
Next, we are given that out of the baby girls born, 12% are premature. To find the probability of a premature baby girl being born, we need to multiply the probability of being a girl (44%) by the probability of being premature (12%).
Probability = 44% * 12% = 0.44 * 0.12 = 0.0528
Now, we need to round this probability to the nearest percent. Since the decimal portion is 0.0528, which is closer to 0.05 than 0.06, we round down.
Therefore, the probability of a premature baby girl being born at this hospital is approximately 5%.
In conclusion, based on the given information, the probability of a premature baby girl being born at this hospital is approximately 5%.
To know more about premature , Visit:
https://brainly.com/question/31207840
#SPJ11
Find the equation that represents the proportional relationship in this graph, for
y in terms of
x.
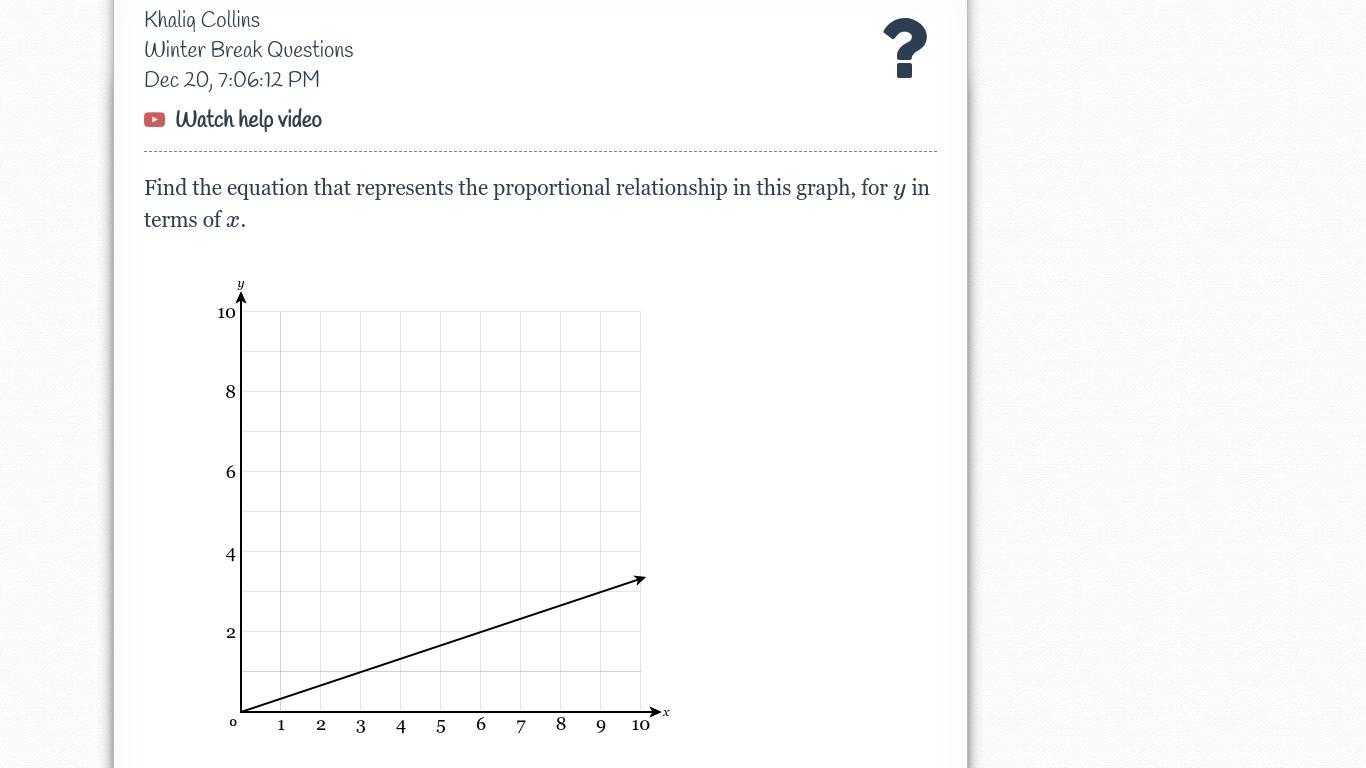
Answers
Answer:
y = -3x
Step-by-step explanation:
The definition of an equation with a proportional relationship with another is that they need to intersect at a 90° angle.
To do this you just have to multiply the slope of the line by its negative reciprocal. So you have to flip the fraction (reciprocal) and then multiply it by -1.
Find the equation of the line:
The line starts at the origion so the y-intercept (b value) is equal to 0.
Looking at slope we can tell that the line has a point at (0, 0) and (3, 1).
The slope between these points is as follows
\(\frac{1 - 0}{3 - 0}\)
So the equation for the first line is y = 1/3x
We then flip the fraction and multiply by -1 to get its proportional line.
y = 1/3x
y = 3x
y = -3x