Students were asked to solve the following equation:
-5x+2=-13
Answers
Answer:
3
Step-by-step explanation:
Step 1:
- 5x + 2 = - 13 Equation
Step 2:
- 5x = - 15 Subtract 2 on both sides
Step 3:
x = - 15 ÷ - 5 Divide
Answer:
x = 3
Hope This Helps :)
Related Questions
help I’m in 5th 14 question

Answers
Find the Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) for the curve →r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0. Round answers to 3 decimal places.
T(0) =0=[sqrt(89)= sqrt(89)]
N(0) =[ ]
B(0) =[ ]
Answers
The tangent vector → \(r(t)=〈4cos(2t),4sin(2t),5t〉\), normal vector at t=0 is given by →N(0) = 〈-1,0,0〉, and binormal vector at t=0 is given by →\(B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector, normal vector, and binormal vector of the given curve are as follows:
Given curve:
→ \(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0
To find: Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) at the point t=0
Tangent vector: To find the tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0,
we need to differentiate the equation of the curve with respect to t.t = 0, we have:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉→r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
Differentiating w.r.t t:→\(r(t) = 〈4cos(2t),4sin(2t),5t〉 → r'(t) = 〈-8sin(2t),8cos(2t),5〉t = 0\),
we have:
→\(r'(0) = 〈-8sin(0),8cos(0),5〉= 〈0,8,5〉\)
Therefore, the tangent vector at t = 0 is given by
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Normal vector:To find the normal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to differentiate the equation of the tangent vector with respect to t.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating w.r.t t:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉t = 0\),
we have:
→\(T'(0) = 〈-16cos(0),-16sin(0),0〉= 〈-16,0,0〉\)
Therefore, the normal vector at t = 0 is given by
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Binormal vector: To find the binormal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to cross-product the equation of the tangent vector and normal vector of the curve.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉\)
The cross product of two vectors:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the binormal vector at t = 0 is given by→B(0) = 〈0, -0.441, -0.898〉
Hence, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are as follows:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The given curve is
→\(r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0.\)
We are asked to find the tangent vector, the normal vector, and the binormal vector of the given curve at t=0.
the tangent vector at t=0. To find the tangent vector, we need to differentiate the equation of the curve with respect to t. Then, we can substitute t=0 to find the tangent vector at that point. the equation of the curve Is:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉\)
At t = 0, we have:
→\(r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
We can differentiate this equation with respect to t to get the tangent vector as:
→\(r'(t) = 〈-8sin(2t),8cos(2t),5〉\)
At t=0, the tangent vector is:
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Next, we find the normal vector. To find the normal vector, we need to differentiate the equation of the tangent vector with respect to t. Then, we can substitute t=0 to find the normal vector at that point.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating this equation with respect to t, we get the normal vector as:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉\)
At t=0, the normal vector is:
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Finally, we find the binormal vector. To find the binormal vector, we need to cross-product the equation of the tangent vector and the normal vector of the curve.
At t=0, we can cross product →T(0) and →N(0) to find the binormal vector.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
The normal vector is:
→N(0) = 〈-1,0,0〉Cross product of two vectors →T(0) and →N(0) is given as:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0 is given by →\(T(0) = 〈0.000,0.898,0.441〉.\)
The normal vector at t=0 is given by →N(0) = 〈-1,0,0〉.
The binormal vector at t=0 is given by →B(0) = 〈0, -0.441, -0.898〉.
To know more about binormal vectors visit
brainly.com/question/31673319
#SPJ11
a manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 433 gram setting. it is believed that the machine is underfilling or overfilling the bags. a 301 bag sample had a mean of 431 grams with a variance of 324 . assume the population is normally distributed. a level of significance of 0.02 will be used. specify the type of hypothesis test.
Answers
The type of hypothesis test to be used in this scenario is a one-sample t-test with a two-tailed alternative hypothesis.
The problem is asking to conduct a hypothesis test to determine whether the bag filling machine works correctly at the 433 gram setting.
The hypothesis test would involve a null hypothesis (H0) and an alternative hypothesis (Ha).
The null hypothesis is typically the hypothesis of "no effect" or "no difference" and is denoted as H0. In this case, the null hypothesis would be that the mean weight of potato chips in the bags filled by the machine at the 433 gram setting is equal to 433 grams. Therefore, the null hypothesis would be:
H0: μ = 433
The alternative hypothesis (Ha) is the hypothesis that we want to test, and it is denoted as Ha. In this case, the alternative hypothesis would be that the mean weight of potato chips in the bags filled by the machine at the 433 gram setting is not equal to 433 grams. Therefore, the alternative hypothesis would be:
Ha: μ ≠ 433
To conduct the hypothesis test, we would need to calculate the test statistic and compare it to the critical value. Since the sample size is large (n=301) and the population variance is unknown, we would use a t-test with a level of significance of 0.02.
If the calculated t-value falls outside the critical t-value, we would reject the null hypothesis and conclude that the bag filling machine does not work correctly at the 433 gram setting.
If the calculated t-value falls within the critical t-value, we would fail to reject the null hypothesis and conclude that there is not enough evidence to suggest that the bag filling machine does not work correctly at the 433 gram setting.
Learn more abou hypothsis test at https://brainly.com/question/24212565
#SPJ11
Michael Had a birthday party. She bought a bag of candy with 96 starbursts, 72 Hershey's, and 68 Reese's. She wanted to use all the candy she bought to make goody bags with the same amount of starbursts, Hershey's and Reese's in each bag. What is the largest number of bags she can make
Answers
Answer: 68 bags.
Step-by-step explanation: She make 68 bags before the Reese's run out.
hope this helps :)
In order to determine if there is a difference between the mean GPA of male and female scholarship athletes, a university administrator obtains a sample of the academic records of past and present scholarship athletes at the university. The administrator reports that the mean GPA (grade point average) of a random sample of 40 male scholarship athletes is 3.02 and the mean GPA of a random sample of 36 female scholarship athletes is 3.11. If there is no difference in the mean GPA of male and female athletes, the probability of obtaining this difference (3.11 – 3.02 = 0.09) or more extreme is approximately 0.287.1. In order to assess the evidence provided by the sample data, what is the appropriate question to ask?a. How likely is it to observe no difference in the mean GPA of male and female scholarship athletes?b. How likely is it to observe a mean GPA difference of 0.09 between male and female scholarship athletes?c. How likely is it to observe a difference of 0.09 or more extreme if there is no difference in the mean GPA for male and female scholarship athletes?d. How likely is it to observe a difference less than 0.09 in the mean GPA of male and female scholarship athletes?2. A university professor does not believe that there is really a difference between the GPA of male and female scholarship athletes, so he looks into how the sample was collected. His investigation shows that the study was given to all of the athletes on the basketball teams exclusively. Based on this information, should the university administration trust the results from this study?a. Yes, because the results were significantb. Yes, because a large enough sample was takenc. No, because not every scholarship athlete part of the studyd. No, because the study was not taken from a random sample of scholarship athletes
Answers
The university administration should not trust the results from this study as it did not take a random sample.
The appropriate question to ask in order to assess the evidence provided by the sample data is, "How likely is it to observe a difference of 0.09 or more extreme if there is no difference in the mean GPA for male and female scholarship athletes?"
This is because the sample data shows a difference of 0.09, so we want to find out how likely it is to observe a difference of this size or greater, given that there is no actual difference between the GPA of male and female scholarship athletes.
Based on the investigation that the professor conducted which revealed that the study was given to all of the athletes on the basketball teams exclusively, the university administration should not trust the results from this study.
This is because the study was not taken from a random sample of scholarship athletes, meaning that the sample did not accurately reflect the population. If the sample does not accurately reflect the population, then the results may be biased and should not be trusted.
For more such questions on scholarship
https://brainly.com/question/26045714
#SPJ11
If for a certain function, f(x)=9 find the following value for the following problems.
(2)f(x)+ 3
(2)f(x)
f(x) + 3
Answers
2(9)=18
(9)+3=12
I'm stuck and I need help quick

Answers
Answer:4
Step-by-step explanation:
The square root of 9 is 3, 3 multiplied by 2 is 6, and 10 - 6 =4.
the diagram below shows three positions, a, b, and c, in the swing of a pendulum, released from rest at point a. [neglect friction.] which statement is true about this swinging pendulum?
Answers
Based on the information provided and considering the terms "pendulum" "positions a, b, and c," and "neglect friction," the true statement about the swinging pendulum is:
At position A, the pendulum has maximum potential energy and no kinetic energy. As it swings towards position B, its potential energy decreases while its kinetic energy increases. At position B, the pendulum has maximum kinetic energy and minimum potential energy. Then, as it moves towards position C, the kinetic energy decreases while the potential energy increases. At position C, it has the same potential energy as at position A, and the cycle repeats.
Potential energy is the energy possessed by an object due to its position or configuration relative to other objects. It is a form of stored energy that has the potential to be converted into other forms of energy and do work.
In the case of an object in a gravitational field, such as a pendulum, potential energy is associated with its vertical position above a reference point, often the ground. The higher the object is lifted, the greater its potential energy. The two most common forms of potential energy are gravitational potential energy and elastic potential energy.
To know more about gravitational potential energy, visit:
https://brainly.com/question/3910603
#SPJ11
The sum of 3 terms in A. P.is - 3 and their product is 8, then sum of squares of the numbers is
Answers
sum of the numbers = - 3
Product of the numbers = 8
Find:sum of squares of the numbers
Solution:Let the three terms be a - d , a , a + d.
sum of the numbers = - 3
→ a - d + a + a + d = - 3
→ 3a = - 3
→ a = - 3/3
→ a = - 1
Also,
Product of the numbers = 8
→ (a - d) * (a) * (a + d) = 8
Putting the value of a and using (a + b) * (a - b) = a² - b² we get,
→ [ (- 1)² - d² ] = 8/ - 1
→ 1 - d² = - 8
→ 1 + 8 = d²
→ 9 = d²
→ d = 3
Hence,
a - d = - 1 - 3 = - 4 a = - 1 a + d = - 1 + 3 = 2Now,
Finding Sum of their squares :
→ (a - d)² + a² + (a + d)²
→ ( - 4)² + ( - 1)² + (2)²
→ 16 + 1 + 4
→ 21
Hence, the sum of the squares of the three terms is 21.
I hope it will help you.
Regards.
30% of 10 is what number
Answers
Answer:
3
Step-by-step explanation:
Answer:
3
Step-by-step explanation:
the word "of" implies to multiply. So we have (30/100)x10=3
A rectangle has an area of 48cm^2 & a perimeter of 38cm. What are the dimensions of the rectangle?
(If you can answer this, I'll give u Brainliest :])

Answers
C............... .......
Answer:
10 is your answer
Step-by-step explanation:
I would love brainliest, thanks!
Which property is demonstrated below?
(a+b)+c=(b+a)+c
A. Commutative property of addition
B.Associative property of addiction
C.Identity property of addition
D.Distributive property
Answers
Answer:
Associative property of addition
Answer:
B.Associative property of addiction
Step-by-step explanation:
to better understand the month-to-month variation of the business, you want to know if average sales across all the months is the same. you want to use an appropriate statistical technique to test your hypothesis. (hint: use a pivot table to aggregate the transaction by month and then reformat the data to be suitable for the appropriate test). from the results of your hypothesis test, what is the p-value?
Answers
To put your theory to the test using the right statistical method. Your hypothesis test yielded a p-value of 0.00810 as a result.
A hypothesis is a proposed explanation or prediction for a phenomenon or observed event, based on limited evidence or observations. It is often used as a starting point for scientific research and experimentation, where a researcher formulates a tentative explanation for a phenomenon, and then tests it through empirical observation and experimentation.
A hypothesis should be testable, falsifiable, and based on previous knowledge or observations. It should be specific and precise, with clear and measurable variables that can be manipulated and observed. A well-formulated hypothesis can guide scientific inquiry, provide a framework for data collection and analysis, and help to generate new knowledge and understanding of the natural world.
To learn more about Hypothesis visit here:
brainly.com/question/29519577
#SPJ4
if x -1/7,evaluate x²+1/x²
Answers
Answer:
\(given \: x = - \frac{1}{7} \)
\(x {}^{2} + \frac{1}{x {}^{2} } \)
\(( - \frac{1}{7} ) {}^{2} + \frac{1}{ ( - \frac{1}{7} ) {}^{2} } \)
\( \frac{1}{49} + \frac{1}{ \frac{1}{49} } \)
\( \frac{1}{49} + \frac{1 \times 49}{1} \)
\( \frac{1}{49} + 49\)
\( \frac{2402}{49} \: or \: 49.02\)
Plot the vector field F(x,y)=(xy,x+y^2) Calculate divF.
Determine where divF>0 and where divF<0.
Answers
The divergence of the vector field F is positive for y > -1/3 and negative for y < -1/3.
To plot the vector field F(x, y) = (xy, x + y^2), we can first visualize the vectors at various points in the xy-plane. Let's choose a range of values for x and y and calculate the corresponding vectors. We'll use a step size of 1 for simplicity.
Here is a sample grid of points and their corresponding vectors:
(x, y) = (-2, -2) -> F(-2, -2) = (4, 2)
(x, y) = (-1, -2) -> F(-1, -2) = (2, 2)
(x, y) = (0, -2) -> F(0, -2) = (0, 2)
(x, y) = (1, -2) -> F(1, -2) = (0, 2)
(x, y) = (2, -2) -> F(2, -2) = (4, 2)
(x, y) = (-2, -1) -> F(-2, -1) = (2, 1)
(x, y) = (-1, -1) -> F(-1, -1) = (1, 1)
(x, y) = (0, -1) -> F(0, -1) = (0, 1)
(x, y) = (1, -1) -> F(1, -1) = (0, 1)
(x, y) = (2, -1) -> F(2, -1) = (2, 1)
... and so on for other values of y and for positive values of y.
To calculate the divergence (divF) of the vector field, we need to find the partial derivatives of the components of F with respect to x and y. Then we sum these partial derivatives.
F(x, y) = (xy, x + y^2)
∂F/∂x = y
∂F/∂y = 1 + 2y
divF = ∂F/∂x + ∂F/∂y = y + (1 + 2y) = 3y + 1
Now, we can analyze where the divergence is positive (divF > 0) and where it is negative (divF < 0).
For divF > 0:
If y > -1/3, then divF > 0.
For divF < 0:
If y < -1/3, then divF < 0.
Know more about vector field here;
https://brainly.com/question/102477
#SPJ11
The standard form of the number represented by the Roman numeral MXCIV is
Answers
Answer:
1094
Step-by-step explanation:
Write an equation of the line that passes through $\left(-1,\ 3\right)$ and is parallel to the line $y=-3x+2$ .
Answers
The equation of the line that passes through point (-1, 3) and parallel to line y = 3x + 2 is
y = 3x + 4How to find the line that passes through point point (-1, 3)As a parallel line part of the qualities include that the slopes of the lines are equal
The equation of line is y = 3x + 2
The slope intercept form of the form as
y = mx + c
where
m = slope
c = intercept
x = input variables
y = output variables
Line has slope, m = 3, a new parallel line of slope 3 passing through point (-1, 3)
(y - y₁) = m (x - x₁)
y - 3 = 3 (x - -1)
y = 3x + 1 + 3
y = 3x + 4
Learn more about linear function:
https://brainly.com/question/29466726
#SPJ1
leo ate 3/5 cup of strawberries and jack ate 7/10 cup of strawberries. how much more did jack eat than leo?
Answers
Jack ate 1/10 cup more strawberries than Leo
The problem states that Leo ate 3/5 cup of strawberries, and Jack ate 7/10 cup of strawberries. We need to find out how much more Jack ate than Leo.
To solve this problem, we first need to find a common denominator for the two fractions. The denominator is the bottom number of a fraction, which represents the total number of equal parts that make up a whole.
The smallest common denominator for 5 and 10 is 10. We can convert the fraction 3/5 into an equivalent fraction with a denominator of 10 by multiplying both the numerator and denominator by 2. This gives us 6/10.
Now, we have two fractions with the same denominator: 6/10 and 7/10. To find out how much more Jack ate than Leo, we can subtract the fraction representing what Leo ate from the fraction representing what Jack ate:
7/10 - 6/10 = 1/10
Therefore, Jack ate 1/10 cup more strawberries than Leo did.
To know more about Fractions here
https://brainly.com/question/1301963
#SPJ4
URGENT!!!!! I NEED HELP ON THIS MATH PROBLEM NOW.

Answers
Answer:
HERE'S YOUR ANSWERHOPE IT WILL HELP YOU!!( ꈍᴗꈍ)( ꈍᴗꈍ)
What is square root raised cosine?
Answers
SRRC is a pulse shaping filter used in digital communications to minimize intersymbol interference and improve the signal-to-noise ratio.
The square root raised cosine (SRRC) is a famous heartbeat molding channel utilized in computerized correspondences, especially in applications like advanced tweak and demodulation. It is intended to limit intersymbol obstruction (ISI) by restricting the data transmission of the sent sign while keeping a consistent envelope.
The SRRC channel is described by a reaction that is like the raised cosine channel, yet with a square root capability applied to the recurrence reaction. This outcomes in a smoother change between the passband and stopband, which assists with decreasing ISI and work on the sign to-clamor proportion.
The SRRC channel is usually utilized in correspondence frameworks that utilization quadrature sufficiency regulation (QAM) or stage shift keying (PSK) tweak plans, as it gives great ghastly control and heartbeat molding properties that are appropriate to these kinds of signs.
To learn ore about square root raised cosine, refer:
https://brainly.com/question/1566472
#SPJ4
The table for the quadratic functions f(x) and g(x) are given.
x f(x) g(x)
−6 36 12
−3 9 3
0 0 0
3 9 3
6 36 12
Determine the type of transformation and the value of k.
g(x) = 3f(x)
g(x) = f(3x)
g of x equals f of one third times x
g of x equals one third times f of x
Answers
The Quadratic functions f(x) and g(x) are related by three types of transformations: vertical stretch, horizontal compression, and vertical compression. In all cases, the value of k is 0.
The values of two quadratic functions, f(x) and g(x), for different values of x. To determine the type of transformation and the value of k between these functions, we can use the given equations:
g(x) = 3f(x)
g(x) = f(3x)
g(x) = (1/3)f(x)
First, let's consider the transformation between g(x) and f(x) given by g(x) = 3f(x). We can see from the table that g(x) is equal to 3 times f(x) for all values of x. This represents a vertical stretch transformation, where the function g(x) is stretched by a factor of 3 compared to f(x). The value of k in this case is 0, as the graphs of f(x) and g(x) intersect at the x-axis, where f(x) = g(x) = 0.
Next, let's consider the transformation given by g(x) = f(3x). We can see from the table that g(x) has the same values as f(x) for x values that are one third of the values for f(x). This represents a horizontal compression transformation, where the function f(x) is compressed by a factor of 1/3 compared to g(x). The value of k is again 0, as the graphs of f(x) and g(x) intersect at the x-axis.
Finally, let's consider the transformation given by g(x) = (1/3)f(x). We can see from the table that g(x) has the same values as f(x) for all values of x, but each value is one third of the corresponding value for f(x). This represents a vertical compression transformation, where the function g(x) is compressed by a factor of 1/3 compared to f(x). The value of k is again 0, as the graphs of f(x) and g(x) intersect at the x-axis.
the given table shows that the quadratic functions f(x) and g(x) are related by three types of transformations: vertical stretch, horizontal compression, and vertical compression. In all cases, the value of k is 0.
To know more about Quadratic functions.
https://brainly.com/question/1214333
#SPJ11
if z is a standard normal variable, find the probability that z lies between −2.41 and 0. round to four decimal places.
Answers
The probability that z lies between -2.41 and 0 is approximately 0.9911.
What is the probability of z falling within a specific range?To find the probability that a standard normal variable, z, falls within a specific range, we can use the standard normal distribution table or a statistical calculator.
In this case, we want to find the probability that z lies between -2.41 and 0. By referencing the standard normal distribution table or using a calculator, we can determine the area under the curve corresponding to this range. The resulting value represents the probability of z falling within that range.
Approximately 0.9911 is the probability that z lies between -2.41 and 0 when rounded to four decimal places. This means that there is a high likelihood (approximately 99.11%) that a randomly chosen value of z from a standard normal distribution falls within this range.
Learn more about probability
brainly.com/question/31828911
#SPJ11
The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b). True False
Answers
The statement "The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b)" is False.
In a uniform distribution, the probability density function (PDF) is constant within the interval [a, b]. The height of the PDF represents the density of the probability distribution at any given point within the interval. Since the PDF is constant, the height remains the same throughout the interval.
To determine the height of the PDF, we need to consider the interval length. In a uniform distribution defined on the interval [a, b], the height of the PDF is 1/(b - a) for the PDF to integrate to 1 over the entire interval. This means that the total area under the PDF curve is equal to 1, representing the total probability within the interval [a, b].
Therefore, the correct statement is that the height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is not 1/(a - b), but rather it is a constant value necessary for the PDF to integrate to 1 over the interval, i.e., 1/(b - a).
Learn more about uniform distribution here:
https://brainly.com/question/32291215
#SPJ11
An amusement park has 24,000 visitors per day when it charges $30 per person. For each $1 increase in price,
the park loses about 500 visitors. How much should the park charge to maximize daily revenue? What is the
maximum daily revenue?
Answers
R(x)=-100x^2+1200x+16000
(-8,0) and (20,0)
$14, cost that gives maximum revenue.
1400 visitors that give max rev.
x: price increase
When price = 8, visitors = 2000
For each increase(x) of 1 in price, visitors decrease by 100
price = 8 + x
visitors = 2000 - 100x
1. Revenue = price * visitors
R(x) = (8+x) (2000-100x)
R(x) = 16,000 - 800x + 2,000x - 100x²
R(x) = -100x² + 1,200x + 16,000
2. Coordinates of maximum point
R(x) is parabola curving down. Maximum point is at vertex
Vertex has x-coordinate = -b/2a
x = -1200/-200 = 6
R(6) = -100*36 + 1,200*6 + 16,000 = 19,600
Maximum point (6, 19600)
3. Admission cost / maximum revenue
Maximum revenue occurs when price increase = 6
Cost = 8 + 6 = 14
Admission cost of $14 gives maximum revenue
4. Number of visitors:
Visitors = 2000 - 100x = 2000 - 600 = 1400
Given r(3,7,-1), S(10,-4,0) find an ordered triple that represents RS and find the magnitude of RS. a.(5,-11,3), 3sqrt19 b.(7,-11,1), 3sqrt19 c.(5,-11,3), 7sqrt15 d.(7,-11,1), 7sqrt15
Answers
Answer:
\(|RS| = \sqrt[3]{19}\)
Step-by-step explanation:
The computation of the magnitude is shown below:
Data provided in the question
Given points
R(3,7,-1), S(10,-4,0)
Now the distance lies between R and S
RS = (10 ,-4, 0) - ( 3 ,7, -1 )
= (10 - 3, -4 - 7, 0 - (- 1))
= (7, - 11, 1 )
After that, the magnitude is determined by using the following calculation part
\(|RS| = \sqrt{(7)^2 + (-11)^2 + (1)^2} \\\\ = \sqrt{49 + 121 + 1} \\\\ = \sqrt{121}\\\\ = \sqrt[3]{19}\)
Find the missing side length

Answers
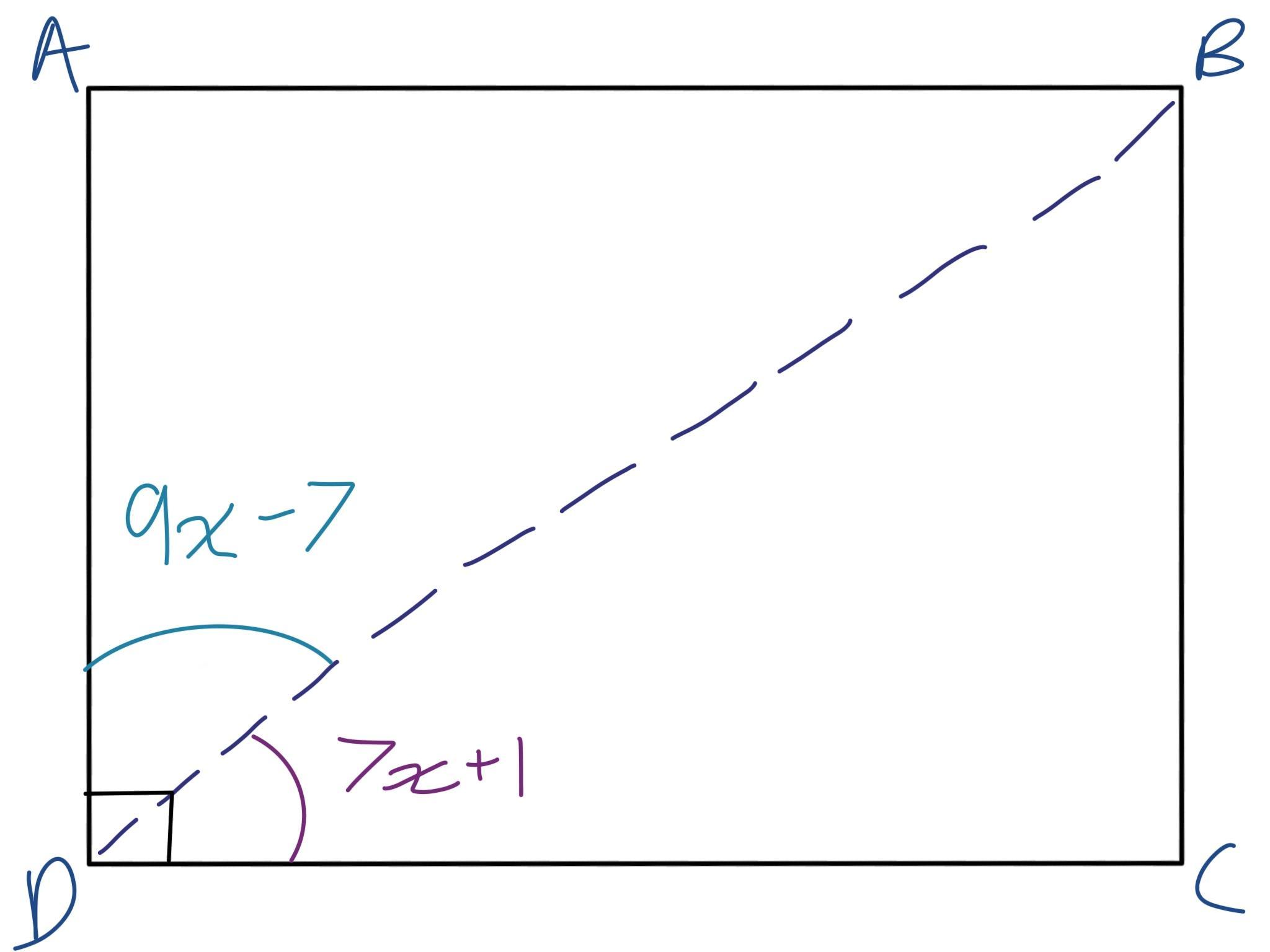
Quadrilateral ABCD is a rectangle.
If BDC = 7x + 1 and ADB=9x - 7, find BDC.
Answers
\(\huge\boxed{45^\circ}\)
See the attached diagram.
Together, angles BDC and ADB form a right angle, which is 90 degrees.
The angles are split straight down the middle, meaning they're equal to each other. This means each one is equal to half of 90 degrees, which is 45 degrees.
What is this number rounded to the nearest tenth ?

Answers
Someone help plz and please make sure it’s right!!!

Answers
Answer:
11
Step-by-step explanation:
The angles of a triangle add up to 180 degrees (always). 5*11 is 55. 55+80+45=180. Hope this helps!
What is the value of X?

Answers
Answer:
The horizontal value in a pair of coordinates: how far along the point is. The X Coordinate is always written first in an ordered pair of coordinates (x,y), such as (12,5). In this example, the value "12" is the X Coordinate. Also called "Abscissa"
Step-by-step explanation: