Subtract 4x4 + 2x2 +5 from the sum of 2x4 – 4x² – 3 and 3x4 – 3x2 +9.
Answers
Answer:
10
Step-by-step explanation:
Related Questions
Two-thirds of a number increased by 3 is 11. What is the number?
Answers
subtract 3 from both sides
2/3x = 8
divide both sides by 2/3 or multiply by its inverse 3/2 to get x by itself.
x = 12
Find the scale factor of the similar shapes below. For your answer please only input the number. Do not include units with your answer.

Answers
Answer:
x is 12
Step-by-step explanation:
7.5÷5=1.5
1.5×8=12
Obtuse triangle. Step 1: Suppose angle A is the largest angle of an obtuse triangle. Why is cosA negative? Step 2: Consider the law of cosines expression for a 2and show that a 2>b2+c2Step 3: Use Step 2 to show that a>b and a>c Step 4: Use Step 3 to explain what triangle ABC satisfies A=103 ∘,a=25, and c=30
Answers
CosA is negative for the largest angle in an obtuse triangle. Using the law of cosines, a²>b²+c², a>b, and a>c are derived.
Step 1: As the obtuse triangle has the largest angle A (more than 90 degrees), the cosine function's value is negative.
Step 2: By applying the Law of Cosines in the triangle, a²>b²+c², which is derived from a²=b²+c²-2bccosA, and hence a>b and a>c can be derived.
Step 3: From the previously derived inequality a²>b²+c², we can conclude that a>b and a>c as a²-b²>c². The value of a² is greater than both b² and c² when a>b and a>c.
Therefore, the largest angle of an obtuse triangle is opposite the longest side.
Step 4: In triangle ABC, A=103°, a=25, and c=30.
a² = b² + c² - 2bccos(A),
a² = b² + 900 - 900 cos(103),
a² = b² + 900 + 900 cos(77),
a² > b² + 900, so a > b.
Similarly, a² > c² + 900, so a > c.
Therefore, triangle ABC satisfies a>b and a>c.
To know more about the obtuse triangle visit:
https://brainly.com/question/3250447
#SPJ11
\((3x3)+(3x5)-(2x-2)\)
Answers
9x + 15x - 2x + 2
22x + 2
This expression can be simplified down to
22x + 2
9 + 15 -2x-2
24-2x-2
22-2x divide
11
for a fundraiser, there is a raffle with 800 tickets, each costing $15. 1 ticket will win a $400 prize, 4 tickets will win a $200 prize, 12 tickets will win a $125 prize, 30 tickets will win a $60 prize, and the remaining tickets will win nothing. if you buy a ticket, what is the expected winnings per ticket? question options:
Answers
The expected winning and the value of that prize, which gives an expected winning is c. $3.13 per ticket.
The expected winnings per ticket in the raffle can be calculated by adding the products of the probability of the expected value of winning each prize. The predicted wins per ticket may be computed as the total of each prize's value multiplied by its probability of winning, i.e.
Expected winnings per ticket
= (1/800) × $400 + (4/800) × $200 + (12/800) × $125 + (30/800) × $60 + (753/800) × $0
If we condense the equation, we obtain:
Calculating the total wins anticipated per ticket
= $0.50 + $1.00 + $1.88 + $0.75 + $0
Expected winnings per ticket = $3.13
Therefore, if you buy a ticket, the expected winnings per ticket are $3.13.
Read more about equation on:
https://brainly.com/question/25976025
#SPJ4
Complete question:
For a fundraiser, there is a raffle with 800 tickets, each costing $15. 1 ticket will win a $400 prize, 4 tickets will win a $200 prize, 12 tickets will win a $125 prize, 30 tickets will win a $60 prize, and the remaining tickets will win nothing. if you buy a ticket, what are the expected winnings per ticket? question options:
a) $5.36
b) $5.63
c) $5.33
d) $5.66
Answer this, please.

Answers
13 runners
Just add up the number that all the bars hit and you get 13
Happy answering!
PLSSSSSSSSS HELPPPPPOPPPOP

Answers
Answer:
Step-by-step explanation:
Triangle B is a(n) ______________________ of Triangle A?
A) Reduction
B) Enlargement

Answers
Answer:
Enlargment
Step-by-step explanation:
Calla bought 8 writing utensils for a total of $30. Pens cost $4 each and pencils cost $3 each. How many pens did she buy?
Answers
Explanation:
Can someone tell me if I’m right on this one?

Answers
Answer:
No, it's -1 + -6 = -7
Step-by-step explanation:
The first arrow goes left -1 and the other one goes left -6, to get -7
n airplane flies due west at an airspeed of 434 mph. The wind blows in the direction of 39° south of west at 58 mph. What is the ground speed of the airplane? What is the bearing of the airplane? 434 mph 39° 58 mph a. The ground speed of the airplane is b. The bearing of the airplane is mph. south of west.
Answers
The ground speed of the airplane is approximately 413 mph and the bearing is approximately 28° south of west.
To solve for the ground speed and bearing of the airplane, we can use vector addition. We can represent the airspeed and wind velocity as vectors, with the airspeed vector pointing due west and the wind velocity vector pointing 39° south of west.
We can then add these two vectors using vector addition, which involves adding the x-components and y-components separately. The resulting vector represents the actual velocity of the airplane relative to the ground.
To find the ground speed, we simply take the magnitude of this resulting vector, which gives us the speed of the airplane relative to the ground. To find the bearing of the airplane, we can use trigonometry to find the angle between the resulting vector and the due west direction.
To know more about speed here.
https://brainly.com/question/4199102
#SPJ4
find an equation of the tangent line to the curve at the given point. y = 2ex cos(x), (0, 2)
Answers
The equation of the tangent line to the curve `y = 2ex cos(x)` at the point (0,2) is given by `y = 2ex + 2`.
To find an equation of the tangent line to the curve at the given point (0,2) whose equation is given by `y = 2ex cos(x)`, we need to determine the derivative `y'` of `y = 2ex cos(x)` first. Using the product rule, we have;
`y = 2ex cos(x)`...let `u = 2ex` and `v = cos(x)`, then `u' = 2ex` and `v' = -sin(x)`.`y' = u'v + uv'` `= 2ex cos(x) - 2ex sin(x)` `= 2ex(cos(x) - sin(x))`
Therefore, the derivative of `y = 2ex cos(x)` is `y' = 2ex(cos(x) - sin(x))`.
The equation of the tangent line to the curve at the point (0,2) is obtained by using the point-slope formula, which is given by: `y - y1 = m(x - x1)`where `(x1,y1)` is the point of tangency, `m` is the slope of the tangent line.
Substituting the values of `m`, `x1` and `y1`, we obtain: `m = y' |(0,2)` `= 2e(1 - 0)` `= 2e`Using the point-slope formula with `(x1,y1) = (0,2)` and `m = 2e`, we have: `y - 2 = 2e(x - 0)` `y - 2 = 2ex` `y = 2ex + 2`
More on tangent line: https://brainly.com/question/28994498
#SPJ11
Which of the following is a solution of this equation?
A.
(5,0)
B.
(-1, 1)
C.
(3,-1)
D.
(-2,-3)

Answers
Answer:
D. (-2,-3)
Step-by-step explanation:
substitute the point values of \(x\) and \(y\) into the equation \(y=\frac{1}{2}x-2\)
A. \(0=\frac{1}{2}(5)-2\)
\(0=2.5-2\)
\(0\) ≠ \(0.5\)
B. \(1=\frac{1}{2}(-1)-2\)
\(1=-.5-2\)
\(1\) ≠ \(-2.5\)
C. \(-1=\frac{1}{2}(3)-2\)
\(-1=1.5-2\)
\(-1\) ≠ \(-0.5\)
D. \(-3=\frac{1}{2}(-2)-2\)
\(-3=-1-2\)
\(-3=-3\)
What is the ratio of future earnings to present earnings for a teacher that currently makes $20/hour and 20 years from now expects to earn $40/hour?
Answers
The ratio of Future earnings to present earnings for the teacher is 2. This means that the teacher expects to earn twice as much per year in 20 years as they currently do.
The ratio of future earnings to present earnings, we need to compare the amount of money the teacher will make in the future to the amount of money they make now. Let's assume that the teacher works the same number of hours per year over the next 20 years, so we can compare their annual earnings.
The teacher currently makes $20/hour, so their current annual earnings are:
$20/hour x hours worked per year = current annual earnings
We don't know how many hours the teacher works per year, so we'll leave this as a variable for now.
In 20 years, the teacher expects to earn $40/hour, so their future annual earnings will be:
$40/hour x hours worked per year = future annual earnings
To find the ratio of future earnings to present earnings, we simply divide the future annual earnings by the current annual earnings:
(future annual earnings) / (current annual earnings)
= ($40/hour x hours worked per year) / ($20/hour x hours worked per year)
= $40/$20
= 2
So the ratio of future earnings to present earnings for the teacher is 2. This means that the teacher expects to earn twice as much per year in 20 years as they currently do. However, it's worth noting that this calculation assumes that the number of hours worked per year remains constant over the 20-year period. If the teacher's working hours change, the actual ratio of future earnings to present earnings may be different.
To know more about Future earnings.
https://brainly.com/question/29852009
#SPJ11
A school is arranging a field trip to the zoo. The school spends 796.65 dollars on passes for 45 students and 2 teachers. The school also spends 402.30 dollars on lunch for just the students. How much money was spent on a pass and lunch for each student?
Answers
Answer: 25.89
Step-by-step explanation: first I do 796.65÷47 which gives us 16.95 and then I do 402.30÷45 which gives us 8.94 and then I add 8.94 and 16.95 together which is 25.89
Is 82 inches grater than 5feet and 10 inches
Answers
Answer:
False, 82 inches is not greater than 5 feet and 10 inches
Step-by-step explanation:
1 feet = 12 inches
5x12=60+10=70
82 is greater than 70.
Help asap have lesss then 14 minutes please

Answers
Answer:
m∠B = 31°
Step-by-step explanation:
To find m∠B, we use the theory that in order to get it we must find the difference between the two arcs GM and VR and dividing it into 2
When putting this to equation we get:
m∠B = \(\frac{1}{2}\) * (VR - GM) = \(\frac{1}{2}\) * ( 94° - 32°) = \(\frac{1}{2}\)(62°) = 31°
pls pls help asap pls

Answers
Answer:
The answer is option 2
Step-by-step explanation:
Working out above

à = 22 +33 B = -1 +23 Ā· B = 4 The angle between A and B is (in degrees):
Answers
The angle between vectors A and B is approximately 89.78 degrees.
To find the angle between vectors A and B, we can use the dot product formula:
A · B = |A| |B| cos(θ)
Given that Ā· B = 4 and knowing the magnitudes of vectors A and B:
|A| = √(22² + 33²)
= √(484 + 1089)
= √(1573)
≈ 39.69
|B| = √((-1)² + 23² )
= √(1 + 529)
= √(530)
≈ 23.02
Substituting the values into the dot product formula:
4 = (39.69)(23.02) cos(θ)
Now, solve for cos(θ):
cos(θ) = 4 / (39.69)(23.02)
cos(θ) ≈ 0.0183
To find the angle θ, we take the inverse cosine (arccos) of 0.0183:
θ = arccos(0.0183)
θ ≈ 89.78 degrees
Therefore, the angle between vectors A and B is approximately 89.78 degrees.
Learn more about Angle Between Vectors at
brainly.com/question/30900097
#SPJ4
25. a 2018 pew research center survey found that more americans believe they could give up their televisions than could give up their cell phones (pew research website). assume that the following table represents the joint probabilities of americans who could give up their television or cell phone. could give up television could give up cellphone yes no yes 0.31 0.17 0.48 no 0.38 0.14 0.52 0.69 0.31 a. what is the probability that a person could give up her cell phone? (4 points) b. what is the probability that a person who could give up her cell phone could also give up television? (4 points) c. what is the probability that a person who could not give up her cell phone could give up her television? (4 points) d. is the probability a person could give up television higher if the person could not give up a cell phone or if the person could give up a cell phone? (4 points)
Answers
(a)Probability that a person could give up cell phone = 0.48
(b)Probability that a person who could give up her cell phone also could give up television is 0.65
(c) Probability that a person who could not give up a cell phone could give up television is 0.73
What is Probability?
Calculating the likelihood of experiments happening is one of the branches of mathematics known as probability. We can determine everything from the likelihood of receiving heads or tails when tossing a coin to the likelihood of making a research blunder, for instance, using a probability. It is crucial to grasp this branch's most fundamental concepts in order to fully comprehend it, including the formula for computing probabilities in equiprobable sample spaces, the likelihood of two events joining together, the probability of the complementary event, etc.
According to the given question:
a. Probability that a person could give up cell phone = 0.48
b. Probability that a person who could give up her cell phone also could give up television
= P(give up cell phone and TV)/p(give up cell phone)
= 0.31/0.48
= 0.6458
= 0.65
c. Probability that a person who could not give up a cell phone could give up television is
= P(could not give up cellphone and could give up TV)/P(could not give up cell phone)
= 0.38/0.52
= 0.73
d. The probability a person could give up television is higher for persons who couldn't give up cell phones than for those who could give up their cell phones.
Hence,
(a)Probability that a person could give up cell phone = 0.48
(b)Probability that a person who could give up her cell phone also could give up television is 0.65
(c) Probability that a person who could not give up a cell phone could give up television is 0.73
To learn more about Probability, visit:
brainly.com/question/13604758
#SPJ4
NEED HELP ASAP PLEASEE

Answers
Answer:
The line is tangent.
Step-by-step explanation:
For the line to be tangent ∠NLM must be 90°.
Because we only have side lengths we can use Pythagorean theorem to prove that ΔNLM is a right triangle making ∠NLM a right angle.
Pythagorean theorem states:
\(a^{2} +b^{2} =c^{2}\)
Substitute values
Because side NM is opposite ∠LNM if the triangle is a right triangle that would be the hypotenuse so we will use that value for c^2. Variable a and b are interchangeable.
\(6^{2} + 8^{2} = 10^2\)
\(36 + 64 = 100\)
Add
\(100 = 100\)
Because 100 does equal 100 ΔLNM is a right triangle making ∠LNM a right angle so therefore line LM is tangent to the circle.
Question 1 (Multiple Choice Worth 2 points)
(Irrational Numbers MC)
Approximate -12 + √32 to the nearest tenth.
O-6.3
O-5.7
O 5.7
O 6.3
Answers
Answer: -6.3
Step-by-step explanation:
\(-12+\sqrt{32\\\)
\(-12+2^2\sqrt{2\)
\(-12+4\sqrt{2\) and that is approx -6.3
For this, we need to evaluate the approximate value of root 32, that is equal to : 5.65
we simply need to put the approximate valuw in expression and find the result.
\( \longrightarrow \tt - 12 + \sqrt{32} \)
\( \longrightarrow \tt - 12 + 5.65\)
\( \longrightarrow \tt - 6.34\)
\(\longrightarrow \tt \approx - 6.3\)
Hence, the first option over there is the most suitable choice.
Hope it helps -',...,'-The effectiveness of a blood-pressure drug is being investigated. An experimenter finds thaton average, the reduction in systolic blood pressure is 49 for a sample of size 25 and standard deviation 15. Estimate how much the drug will lower a typical patient's systolic blood pressure (using a 80% confidence level) Give your answers to one decimal place and provide the point estimate with its margin of error.
Answers
Solution:
Given:
\(\begin{gathered} \bar{x}=49 \\ n=25 \\ s=15 \\ C.I=80\text{ \%} \end{gathered}\)Using the formula;
\(C.I=\bar{x}\pm z\frac{s}{\sqrt{n}}\)The z-score for 80% confidence interval is given by 1.28
Hence,
\(\begin{gathered} =49\pm1.28(\frac{15}{\sqrt{25}}) \\ =49\pm1.28(\frac{15}{5}) \\ =49\pm1.28(3) \\ =49\pm3.84 \end{gathered}\)Hence, the point estimate with its margin of error to one decimal place is;
\(49\pm3.8\)what is the probability that a seven-card poker hand contains 1. four cards of one kind and three cards of a second kind? 2. three cards of one kind and pairs of each of two different kinds? 3. pairs of each of three different kinds and a single card of a fourth kind? 4. pairs of each of two different kinds and three cards of a third, fourth, and fifth kind? 5. cards of seven different kinds? 6. a seven-card flush? 7. a seven-card straight? 8. a seven-card straight flush?
Answers
The probability is: 0.00198 or about 1 in.
To calculate the probability of getting four cards of one kind and three cards of a second kind, we need to choose the rank for the four cards (13 choices), then choose four suits for those cards (4 choices each), choose the rank for the three cards (12 choices), and then choose two suits for those cards (4 choices each). The total number of seven-card poker hands is 52 choose 7. Therefore, the probability is:
(13 * 4^4 * 12 * 4^2) / (52 choose 7) ≈ 0.0024 or about 1 in 416
To calculate the probability of getting three cards of one kind and pairs of each of two different kinds, we need to choose the rank for the three cards (13 choices), then choose three suits for those cards (4 choices each), choose the ranks for the two pairs (12 choices for the first and 11 choices for the second), and then choose two suits for each pair (4 choices each). The total number of seven-card poker hands is 52 choose 7. Therefore, the probability is:
(13 * 4^3 * 12 * 4^2 * 11 * 4^2) / (52 choose 7) ≈ 0.0475 or about 1 in 21
To calculate the probability of getting pairs of each of three different kinds and a single card of a fourth kind, we need to choose the ranks for the three pairs (13 choose 3), then choose two suits for each pair (4 choices each), choose the rank for the single card (10 choices), and then choose one suit for that card (4 choices). The total number of seven-card poker hands is 52 choose 7. Therefore, the probability is:
(13 choose 3) * (4^2)^3 * 10 * 4 / (52 choose 7) ≈ 0.219 or about 1 in 5
To calculate the probability of getting pairs of each of two different kinds and three cards of a third, fourth, and fifth kind, we need to choose the ranks for the two pairs (13 choose 2), then choose two suits for each pair (4 choices each), choose the ranks for the three other cards (10 choices for the first, 9 choices for the second, and 8 choices for the third), and then choose one suit for each card (4 choices each). The total number of seven-card poker hands is 52 choose 7. Therefore, the probability is:
(13 choose 2) * (4^2)^2 * 10 * 4 * 9 * 4 * 8 * 4 / (52 choose 7) ≈ 0.221 or about 1 in 5
To calculate the probability of getting cards of seven different kinds, we need to choose the ranks for the seven cards (13 choose 7), then choose one suit for each card (4 choices each). The total number of seven-card poker hands is 52 choose 7. Therefore, the probability is:
(13 choose 7) * 4^7 / (52 choose 7) ≈ 0.416 or about 2 in 5
To calculate the probability of getting a seven-card flush, we need to choose one suit (4 choices), and then choose seven cards of that suit (13 choose 7). The total number of seven-card poker hands is 52 choose 7. Therefore, the probability is:
4 * (13 choose 7) / (52 choose 7) ≈ 0.00198 or about 1 in
To learn more about probability visit:
https://brainly.com/question/11234923
#SPJ11
Find the remaining trigonometric ratios. cos(x) = − 1/8, π < x < 3π/2
Answers
We know that cos(x) = -1/8 and π < x < 3π/2. Since cosine is negative in the third and fourth quadrants, we can draw a reference triangle in the third quadrant with a horizontal leg of 1 and a vertical leg of -8.
Using the Pythagorean theorem, we can find the length of the hypotenuse:
c^2 = a^2 + b^2
c^2 = 1^2 + (-8)^2
c^2 = 65
c = √65
Therefore, the reference triangle in the third quadrant looks like this:
|
|___
x
-----
√65
Now, we can use the trigonometric ratios to find the remaining sides and angles:
sin(x) = -√(65)/8
tan(x) = -√(65)/1 = -√(65)
csc(x) = -8/√(65) = -8√(65)/65 = (-8/65)√(65)
sec(x) = -1/√(65) = (-1/65)√(65)
cot(x) = -1/√(65) = (-1/65)√(65)
Therefore, the remaining trigonometric ratios are:
sin(x) = -√(65)/8
tan(x) = -√(65)
csc(x) = (-8/65)√(65)
sec(x) = (-1/65)√(65)
cot(x) = (-1/65)√(65)
To learn more about trigonometric visit:
https://brainly.com/question/29156330
#SPJ11
slope= 1/4, y intercept=2
Answers
boxplot summarizes the heights of a group of people who participate in a weekend biking club. Which of the following statements is supported by the boxplot?
A) The mean height is 67 inches.
B) The number of people with height at least 70 inches is greater than the number of people with height at most 62 inches.
C) The number of people with height at least 67 inches is less than the number of people with height at most 67 inches.
D) Approximately 50% of the people have a height between 62 inches and 70 inches.
E) Approximately 25% of the people have a height greater than 62 inches.
Answers
Approximately 50% of the people have a height between 62 inches and 70 inches. This is the statement that is supported by the boxplot.
The problem is solved by constructing a histogram by using the given data. So by that histogram we can conclude the given statement that is supported by the boxplot.
Given that, the boxplot summarizes the heights of a group of people who participate in a weekend biking club
The mean height is 67 inches. The number of people with height at least 70 inches is greater than the number of people with height at most 62 inches.
The number of people with height at least 67 inches is less than the number of people with height at most 67 inches. Approximately 50% of the people have a height between 62 inches and 70 inches. Approximately 25% of the people have a height greater than 62 inches.
Therefore, the statement is Approximately 50% of the people have a height between 62 inches and 70 inches. This is the statement that is supported by the boxplot.
Learn more about height here
brainly.com/question/27996736
#SPJ4
What is the missing value
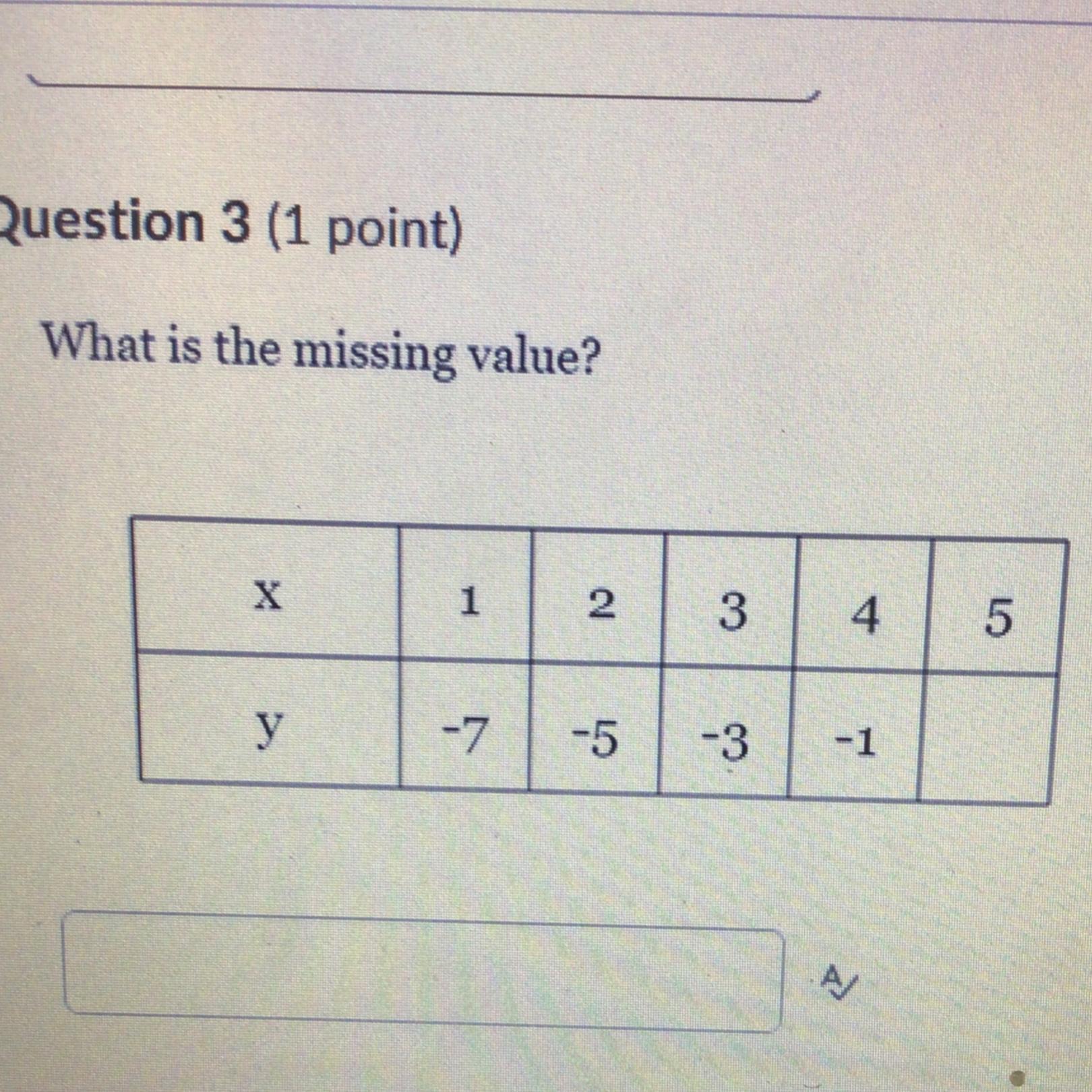
Answers
Answer:
I am not entirely sure but I think it is 1.
Step-by-step explanation:
Don't quote me on this though. Please tell me if I am wrong.
Consider a linear time-invariant (LTI) and causal system described by the following differential equation: ý" (t) +16(t) = z (t)+2x(t) where r(t) is the input of the system and y(t) is the output (recall that y" denotes the second-order derivative, and y' is the first-order derivative). Let h(t) be the impulse response of the system, and let H(s) be its Laplace transform. Compute the Laplace transform H(s), and specify its region of convergence (ROC).
Answers
The Laplace transform H(s) of the system is 1 / (s^2 + 16), and its region of convergence (ROC) is Re(s) > 0.
To compute the Laplace transform H(s) of the given system, we need to take the Laplace transform of the differential equation. Let's denote the Laplace transform of a function x(t) as X(s).
Taking the Laplace transform of the given differential equation, we have: s^2Y(s) + 16Y(s) = Z(s) + 2X(s)
Rearranging the equation, we get: H(s) = Y(s) / X(s) = 1 / (s^2 + 16)
The transfer function H(s) represents the Laplace transform of the impulse response h(t) of the system. The impulse response h(t) is the output of the system when the input is an impulse function.
Now, let's determine the region of convergence (ROC) of H(s). The ROC is the set of values of s for which the Laplace transform converges. In this case, the denominator of H(s) is s^2 + 16, which is a polynomial in s.
The system is causal, which means it must be stable and have a ROC that includes the imaginary axis to the right of all poles. The poles of the transfer function H(s) are located at s = ±4j (j denotes the imaginary unit). Therefore, the ROC of H(s) is Re(s) > 0.
Therefore, the Laplace transform H(s) of the system is 1 / (s^2 + 16), and its region of convergence (ROC) is Re(s) > 0.
Learn more about region of convergence
https://brainly.com/question/17019250
#SPJ11
he coordinates of three corners of a square are (–2, 0), (1, 0), and (1, –3). Use this information to complete the following tasks.
Graph the three points given.
Determine the coordinates of the fourth corner of the square.
Draw the square.
Determine the perimeter of the square.
Answers
The coordinates of point D on the graph are (2,-2). the square has a surface area of 25 square units. The perimeter of the square p is 20 units.
How to plot the coordinate on the graph?A (2,3), B (-3, 3), and C (-3, -2) are the given points.
In the graph below, the points are plotted.
The coordinates of point D on the graph are (2,-2).
In this case, AB = 5 units [from the graph].
The square's area = side * side
ABCD's square area = AB *AB
= 5×5
= 25 square units.
As a result, the square has a surface area of 25 square units.
The perimeter of the square p = 4 * side
p = 4 *5 = 20 units.
Learn more about area of square here.
https://brainly.com/question/1658516
#SPJ1
Similar question:
The three vertices of a square are A (2,3), B(-3, 3), and C (-3, -2). Plot these points on graph paper and
hence use it to find the coordinates of the fourth vertex. Also, find the area and perimeter of the square.
