Sum of Geometric Series Problem Sn=a+ar+ar^2+...+ar^n-1, S2=3.5, S3=11.375, and r<0. Find a and r.
Answers
We have that
\(\begin{gathered} Sn=a+ar^1+ar^2+...+ar^{n-1} \\ S_2=3.5,S_3=11.375 \end{gathered}\)Now, we have two equations:
\(\begin{gathered} a+ar=3.5 \\ a+ar^1+ar^2=11.375 \end{gathered}\)We have that:
\(S_n=\frac{a\mleft(1-r^n\mright)}{1-r}\)Then, for S2 and S3:
\(\begin{gathered} S_2=\frac{a(1-r^2)}{1-r}=3.5 \\ S_3=\frac{a(1-r^3)}{1-r}=11.375 \end{gathered}\)Then, we have two equations:
\(\begin{gathered} \frac{a(1-r^2)}{1-r}=3.5 \\ \frac{a(1-r^3)}{1-r}=11.375 \end{gathered}\)Now, solving for (1 - r):
\(\begin{gathered} \frac{a(1-r^2)}{3.5}=1-r \\ \frac{a(1-r^3)}{11.375}=1-r \end{gathered}\)We equate them:
\(\frac{a(1-r^2)}{3.5}=\frac{a(1-r^3)}{11.375}\)Now, we can solve for r:
\(\begin{gathered} \frac{a(1-r^2)}{3.5}=\frac{a(1-r^3)}{11.375} \\ \downarrow \\ \frac{1-r^2}{3.5}=\frac{1-r^3}{11.375} \\ \downarrow \\ 11.375\cdot(1-r^2)=3.5(1-r^3) \end{gathered}\)Dividing both sides by 3.5:
\(\begin{gathered} 11.375\cdot(1-r^2)=3.5(1-r^3) \\ \downarrow \\ 3.25(1-r^2)=1-r^3 \\ \downarrow \\ 3.25-3.25r^2=1-r^3 \end{gathered}\)Now, rearraging the equation we have that:
\(r^3-3.25r^2+2.25=0\)From the equation, we have that r has three possible values:
\(\begin{gathered} r_1=3 \\ r_2=_{}1 \\ r_3=-\frac{3}{4}=-0.75 \end{gathered}\)We know this because of the graph of the equation:
Since r < 0, then the solution is:
\(r=-\frac{3}{4}=-0.75\)Since
\(\begin{gathered} a+ar=3.5 \\ \downarrow \\ a(1+r)=3.5 \end{gathered}\)we can find a if we replace r = -3/4:
\(\begin{gathered} a(1-0.75)=3.5 \\ a(0.25)=3.5 \end{gathered}\)Then,
\(a=\frac{3.5}{0.25}=14\)Therefore the values of r and a are:
Answer- r = - 0.75 and a = 14

Related Questions
Find RS. Explain your reasoning.
6x + 5 9x - 4
RS=

Answers
The value of line RS is 23
How to determine the valueFrom the diagram shown, we have that line PS, line PQ, line QR and line RS form a square.
Note that the sides of a square are equal to each other.
The relationship is represented as;
Line PS = Line PQ = Line QR = Line RS
We have that;
Line PS = 6x - 5Line RS = 9x - 4Substitute the expressions
6x - 5 = 9x - 4
Now, collect like terms
6x - 9x = - 4 - 5
Subtract the like terms
-3x = -9
Make 'x' the subject of formula
-3x/-3 = -9/-3
x = 3
Then, RS = 9x - 4 = 9(3) - 4 = 27 - 2 = 23
Hence, the value is 23
Learn more about squares here:
https://brainly.com/question/25092270
#SPJ1
In the figure below, please awnser the question

Answers
Answer:
76
Step-by-step explanation:
Angle bisectors split angles into two. So, angle BAD must be twice of BAC.
Substituting, we get 38*2=76
Challenge An arts academy requires there to be 4 teachers for every 72 students and 3 tutors for every 27 students. How many students does the academy have per teacher? Per tutor? How many tutors does the academy need if it has 81 students?
Answers
ANSWER
a) 18 students per teacher
b) 9 tutors
EXPLANATION
We have that the Arts Academy:
=> requires 4 teachers for every 72 students
=> 3 tutors for every 27 students
a) To find how many students are need per teacher, we have to divide the number of students by the number of teachers.
That is:
72 / 4 = 18 students per teacher
b) To find the number of tutors needed by the Academy, we have that:
3 tutors = 27 students
x tutors = 81 students
Cross multiply:
x * 27 = 3 * 81
=> x = 243 / 27
x = 9
Therefore, 9 tutors are needed for 81 students.
I need help pls!!!!!

Answers
Answer:
AP EURO DBQ RUBRIC. Updated July 2017. Name: DBQ: CONTEXTUALIZATION. Describes a broader historical context
g Gravel is being dumped from a conveyor belt at a rate of 10 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 6 ft high
Answers
Answer:
0.3537 feet per minute.
Step-by-step explanation:
Gravel is being dumped from a conveyor belt at a rate of 10 ft3/min. Since we are told that the shape formed is a cone, the rate of change of the volume of the cone.
\(\dfrac{dV}{dt}=10$ ft^3/min\)
\(\text{Volume of a cone}=\dfrac{1}{3}\pi r^2 h\)
If the Base Diameter = Height of the Cone
The radius of the Cone = h/2
Therefore,
\(\text{Volume of the cone}=\dfrac{\pi h}{3} (\dfrac{h}{2}) ^2 \\V=\dfrac{\pi h^3}{12}\)
\(\text{Rate of Change of the Volume}, \dfrac{dV}{dt}=\dfrac{3\pi h^2}{12}\dfrac{dh}{dt}\)
Therefore: \(\dfrac{3\pi h^2}{12}\dfrac{dh}{dt}=10\)
We want to determine how fast is the height of the pile is increasing when the pile is 6 feet high.
\(When h=6$ feet$\\\dfrac{3\pi *6^2}{12}\dfrac{dh}{dt}=10\\9\pi \dfrac{dh}{dt}=10\\ \dfrac{dh}{dt}= \dfrac{10}{9\pi}\\ \dfrac{dh}{dt}=0.3537$ feet per minute\)
When the pile is 6 feet high, the height of the pile is increasing at a rate of 0.3537 feet per minute.
Mathmatics for Calculus

Answers
The value of function for f'(2) is 0.22.
What is the differentiation?The process of finding derivatives of a function is called differentiation in calculus. A derivative is the rate of change of a function with respect to another quantity.
Given that, f(x)= √(x+3) at the specific point x=2.
f'(2)= \(\lim_{h \to \ 0}\)((f(2+h)-f(2))/h)
Find the derivative using the chain and power rules.
\(f(x)=(x+3)^{\frac{1}{2} }\)
f'(x) = \(\frac{1}{2(x+3)^{\frac{1}{2} }}\)
f'(2)= \(\frac{1}{2(2+3)^{\frac{1}{2} }}\)
f'(2)= \(\frac{1}{2(2+3)^{\frac{1}{2} }}\)
f'(2)= 1/2√5
f'(2)= 1/4.47
f'(2)= 0.22
Therefore, the value of function for f'(2) is 0.22.
To learn more about the differentiation of an equations visit:
https://brainly.com/question/25731911.
#SPJ1
Which expression is equivalent to −30+(−40)+(−70) ?
Answers
Answer:
−30+(−40)+(−70) = -140
Step-by-step explanation:
−30+(−40)+(−70) = -140
Answer:
not what im looking for
Step-by-step explanation:
Here is a vertical algorithm that we can use to find 60.19 – 47.52.Which place value column(s) will require regrouping?Please see image below.
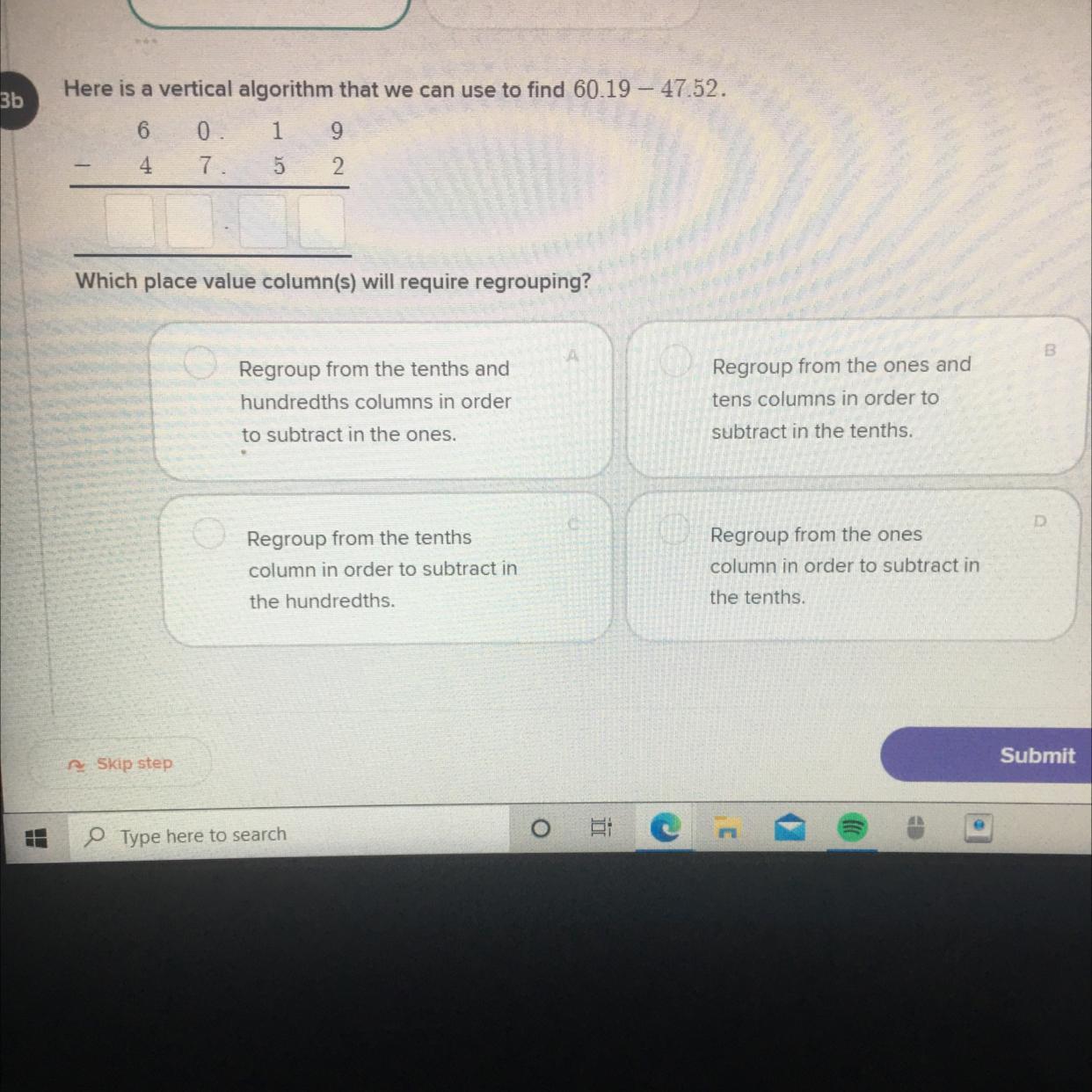
Answers
Regrouping happens when we need to "borrow" value from the higher order digits to perform a subtraction properly. This happens on the tenths, because we need to subtract 5 from 1, which we can't do normally. So we need to regroup from the ones and tens, in order to solve the problem. The correct answer is B.
NO LINKS!! URGENT HELP PLEASE!!!
NOT MULTIPLE CHOICE!!
8. a. Finish the table
b. Name the type of sequence
c. Find the equation for the following sequence

Answers
Answer:
7: 63
8: 73
arithmetic sequence
y = 10x - 7
or f(n) = 10x -7
or
\(a_{n}\) = 3 + (n-1)10
Step-by-step explanation:
the output increases by 10 every time that the input increases by 1. That gives us our common difference or slope. The y intercept is -7. That is the value is you worked backwards until you get to n = 0. The initial value is 3. That is when n is 1.
When n is 3, f(n) is 23
When n is 2, f(n) is 13
When n is 1, f(n) is 3
When n is 0, f(n) is -7
I am not sure if this is clear. I am assuming that you have a lot of knowledge of linear equations and how to write arithmetic sequence. If my explanation is confusing it is me and not you.
Answer:
a. 63,73
b. Arithmetic sequence
c.t(n)=10n-7
Explanation:
a. Here is the completed table:
n | t(n)
4 | 33
5 | 43
6 | 53
7 | 63
8 | 73
b.
The type of sequence is arithmetic.
An arithmetic sequence is a sequence of numbers where the difference between any two consecutive terms is constant.
In this case, the difference between any two consecutive terms is 10.
c.
The equation for the arithmetic sequence is:
t(n)=a+(n-1)d
where:
t(n) is the nth term in the sequencen is the term numberd is the common differencea is the first termFor Question:
d=43-33=10a=?Now
equation becomes:
t(4) = a+(4-1)10
33=a+30
a=33-30
a=3
Now, the Equation becomes
t(n) = 3+(n-1)10
t(n) = 3+10n-10
t(n)=10n-7
Two angle measures of this triangle are 60°. Which type of triangle is it? O A. obtuse O B. scalene O C. equilateral O D. right
plz need help now :(

Answers
Answer:
equilateral
Step-by-step explanation:
all the sides are equal
The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of 9.8% per hour. How many hours does it take for the size of the sample to double?
Note: This is a continuous exponential growth model.
Do not round any intermediate computations, and round your answer to the nearest hundredth.
Answers
For the population to double, it takes around 7.07 hours.
The continuous exponential growth model is given by:
\(N(t) = N0 * e^{rt}\)
Where:
N(t) is the population size at time t
N is the initial population size (at t = 0)
r is the growth rate parameter
t is the time elapsed
We want to find the time t it takes for the population size to double, which means N(t) = 2N. Substituting into the growth model, we get:
\(2N = N * e^{rt}\)
Dividing both sides by N, we get:
\(2 = e^{rt}\)
Taking the natural logarithm of both sides, we get:
ln(2) = rt
Solving for t, we get:
t = ln(2)/r
Substituting r = 0.098 (9.8% as a decimal), we get:
t = ln(2)/0.098
t ≈ 7.07 hours
Therefore, it takes approximately 7.07 hours for the population size to double.
Learn more about exponential growth and decay here:
https://brainly.com/question/17161065
#SPJ1
A wire weighs 18.9 pounds per foot. How much will 17 inches of wire weigh? Round
answer to the nearest tenth [1 foot = 12 inches]
Answers
Answer:
26.8 pounds per foot
Step-by-step explanation:
Since we are looking for 17 inches, we have to find how much each inch of wire weighs by dividing
18.9 / 12 = 1.575
This represents the weight of one inch of wire
Now, we can multiply by 17 to find the weight of 17 inches of wire
1.575 x 17 = 26.775
Lastly, we have to round to the nearest tenth thus our final answer is
26.8
Will give brainliest for correct answer


Answers
Answer:
The first picture on the second page
Step-by-step explanation:
The first picture on the second page would be the answer because it gives exactly one input for each output. It also passes the vertical line test because no point throughout the line creates a vertical line.
Pls help me I am stuck tysm

Answers
a) The initial deposit in the account is given as follows: 1,287.39 euros.
b) The interest rate of the account is given as follows: 3%.
How to obtain the balance using simple interest?The equation that gives the balance of an account after t years, considering simple interest, is modeled as follows:
A(t) = P(1 + rt).
In which the parameters of the equation are listed and explained as follows:
A(t) is the final balance.P is the value of the initial deposit.r is the interest rate, as a decimal.t is the time in years.Considering the balances after 5 and 6 years, the interest rate is obtained as follows:
r = 1524.60/1480.50 - 1
r = 0.03.
Considering the balance after 5 years, the initial deposit is obtained as follows:
P(1 + 0.03 x 5) = 1480.5
P = 1480.5/1.15
P = 1,287.39 euros.
More can be learned about simple interest at https://brainly.com/question/20690803
#SPJ1
given f(x) = 17 - x squared what is the average rate of change in f(x) over the interval [1,5]
Answers
let me write this down
How many cubes with side lengths of 1/2 cm does it take to fill the prism.

Answers
Answer:
24 cubes
Step-by-step explanation:
You can figure this a couple of ways.
I usually find it easiest to figure in terms of the number of cubes each dimension represents. The vertical dimension (3/2 cm) is the length of 3 cubes; the front-back dimension (2 cm) is the length of 4 cubes, and the width (1 cm) is the length of 2 cubes.
The total number of cubes required is the product of the dimensions in cube-lengths: 3×4×2 = 24 cubes.
The function f(x) is shown on the graph.
What is f(0)?
0 only
-6 only
–2, –1, 1, and 3 only
–6, -2,-1, 1 and 3 only
Answers
The function f(x) has five intercepts at -6 only, -2, -1, 1, and 3 only.
The correct answer is D.
The function f(x) has some specific characteristics as shown in the graph.
The graph of f(x) has five intercepts, as can be seen from the graph.
The intercepts of f(x) can be determined by observing where the graph of f(x) crosses the x-axis.
The function f(x) intercepts the x-axis at five different points: -6 only, -2, -1, 1, and 3 only.
At these points, f(x) = 0.
Furthermore, the graph of f(x) is increasing from -∞ to -6, then decreasing from -6 to -2.
The graph of f(x) then increases from -2 to -1, decreases from -1 to 1, increases from 1 to 3, and finally decreases from 3 to +∞.
Hence, we can deduce that the graph of f(x) has a local maximum point at x = -6, a local minimum point at x = -2, and another local minimum point at x = 3.
We can also conclude that f(x) is an odd function, meaning that f(-x) = -f(x).
This can be deduced from the symmetry of the graph about the origin.
Finally, we can see from the graph that the function f(x) is continuous everywhere except at x = -2 and x = 3.
At these points, f(x) is not defined.
The function f(x) has five intercepts at -6 only, -2, -1, 1, and 3 only.
For such more questions on intercepts
https://brainly.com/question/24212383
#SPJ8
What is the solution to the compound inequality: 10<2x-4<20
Answers
Answer:
7 < x < 12
Step-by-step explanation:
To solve this inequality, solve it the same way you do a normal function. Perform the same actions on both sides of the inequality.
\(10 < 2x-4 < 20\\14 < 2x < 24\\7 < x < 12\)
5.
The probability of a family having a baby girl is approximately 50%. A simulation is conducted in
which a coin is flipped three times, recording if the coin landed on "Heads" (H) or "Tails" (T). This
a
trial was conducted 50 times with results shown below.
Heads (H) = Baby Boy
Tails (T) = Baby Girl
Using the simulation above, what is the approximate probability that a family with three
children will have a boy first, a girl second, and a boy third?
Approximately 2%
Approximately 4%
Approximately 6%
Approximately 12%

Answers
So, on solving the provided question, we cans ay that the probability Approximately 2% of boy is HHH, HHT,HTH, TTT, TTH = 4/26
What is probability?Calculating the likelihood that an event will occur or a claim is true is the domain of probability theory, a branch of mathematics. The probability of an event is a number between 0 and 1, where approximately 0 represents how likely the event is to occur and 1 represents certainty.
A probability is a numerical representation of the likelihood or likelihood that a specific event will occur. Probabilities can also be expressed as percentages from 0% to 100% or from 0 to 1. the proportion of occurrences in a full set of equally likely possibilities that lead to a specific occurrence relative to the total number of outcomes.
Here, we have
Heads (H) = Baby Boy
Tails (T) = Baby Girl
the probability Approximately 2% of boy is HHH, HHT,HTH, TTT, TTH = 4/26
To know more about probability visit:
brainly.com/question/11234923
#SPJ1
Find the surface area of the prism.

Answers
Answer:
\(A=202\ cm^2\)
Step-by-step explanation:
Given that,
The dimensions of the prism are 4 cm, 9 cm and 5 cm respectively.
The formula for the surface area of the prism is given by :
\(A=2(lb+bh+hl)\)
Put all the values,
\(A=2(4(9)+9(5)+5(4))\\\\A=2(36+45+20)\\\\A=202\ cm^2\)
So, the required surface area of the prism is equal to \(202\ cm^2\).
Solve using tangent and cosine

Answers
The value of side length x in diagram a) is 4.3mm and side length x in diagram b) is 309.7 m.
What are the sides of the triangle labelled x?The figures in the image are right triangles.
A)
angle D = 17 degree
Adjacent to angle D = 14 mm
Opposite to angle D = x
To solve for the missing side length x, we use the trigonometric ratio.
Note that: tangent = opposite / adjacent
Hence:
tan( 17 ) = x/14
x = tan( 17 ) × 14
x = 4.3mm
B)
angle Z = 82 degree
Adjacent to angle Z = 43.1 m
Hypotenuse = x
Using trigonometric ratio,
cosine = adjacent / hypotenuse
cos( 82 ) = 43.1 / x
x = 43.1 / cos( 82 )
x = 309.7 m
Therefore, the measure of x is 309.7 meters.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Joseph wants to line his garden with a fence that cost $2.25 per foot. The length of the garden is 6 yards and the width is 2.5 yards. what is the total cost?
Answers
Answer:
$38.25
Step-by-step explanation:
Perimeter of a rectangle = 2W + 2L
(where W is the width and L is the length)
Given:
width = 2.5 ydlength = 6 yd⇒ perimeter = (2 x 2.5) + (2 x 6)
= 5 + 12
= 17 yd
Given:
cost of fence = $2.25 per foot⇒ total cost = 17 x 2.25
= $38.25
Perimeter:-
2(L+B)2(6+2.5)2(8.5)17ydToatl cost::
17(2.25)34+4.2538.25$find the slope of the tangent line to the curve y at x. then write the equation of this tangent line. question content area bottom part 1 the slope of the line tangent to the curve y at x is 36. part 2 the equation of the line tangent to the curve y at x is y minus y equals 36 (x minus 3 ).
Answers
the equation of the line tangent to the curve y at x = 3 is y = 36x - 102. The slope of the tangent line to the curve y at x = 3 is 36.
The equation of the line tangent to the curve y at x = 3 can be written using the point-slope form of a line, which is:
y - y1 = m(x - x1)
where m is the slope of the line, (x1, y1) is a point on the line, and m and (x1, y1) are known. In this case, m = 36 and (x1, y1) = (3, y). Substituting these values into the equation above, we get:
y - y = 36(x - 3)
y = 36x - 102
So the equation of the line tangent to the curve y at x = 3 is
y = 36x - 102.
To know more Tangent
https://brainly.com/question/4470346
#SPJ4
In a survey of 2,100 people who owned a certain type of car, 420 said they would buy that type of car again. What percent of the people surveyed were satisfied with the car?
Answers
(420/2,100=0.2)
(0.2*100=20)
Thank you for your help

Answers
Answer:
you are very welcome!
Step-by-step explanation:
which of the following is equivalent to the expression below? √96 - √54+ √24

Answers
Explanation:
The expression that we have is:
\(\sqrt{96}-\sqrt{54}+\sqrt{24}\)And we need to find the equivalent expression.
Step 1. The first step is to simplify the square roots by looking for multiplications that result in the number inside that square root, and that one of those numbers has an exact square root.
Let's start with the square root of 96, we can write 16x6 instead of 96:
And then, since 16 has an exact square root (which is 4) we further simplify the expression to:
\(\sqrt{96}=4\sqrt{6}\)Step 2. We do the same for the other two square roots:
Step 3. Using these results, our expression now is:
\(\sqrt[]{96}-\sqrt{54}+\sqrt{24}=4\sqrt{6}-3\sqrt{6}+2\sqrt{6}\)To find the equivalent expression, since now we have that all of the square roots have the same number inside (6) we can just make the operations with the numbers 4, -3, and 2, and the result is:
\(4\sqrt{6}-3\sqrt{6}+2\sqrt{6}=\boxed{3\sqrt{6}}\)which is option D.
Answer:
D
\(3\sqrt{6}\)

the perimeter of a semicircle protractor is 14.8cm,find it's radius
Answers
The radius of the semicircle protractor is approximately 4.693 cm.
Given,Perimeter of a semicircle protractor = 14.8 cm.
To find:The radius of a semicircle protractor.Solution:We know that the perimeter of a semicircle protractor is the sum of the straight edge of a protractor and half of the circumference of the circle whose radius is the radius of the protractor.
Circumference of a circle = 2πrWhere, r is the radius of the circle.If the radius of the semicircle protractor is r, then Perimeter of a semicircle protractor = r + πr [∵ half of the circumference of a circle =\((1/2) × 2πr = πr]14.8 = r + πr14.8 = r(1 + π) r = 14.8 / (1 + π)r ≈ 4.693\) cm.
for more questions on semicircle protractor
https://brainly.com/question/30188078
#SPJ8
Which of the following sets of angle measures is equivalent to

Answers
ANSWER :
The angles are 150 degrees and 210 degrees
EXPLANATION :
Recall the cosine of 30 degrees.
\(\cos30=\frac{\sqrt{3}}{2}\)From the problem, we need to find the measurement of the angle that will give a cosine value of :
\(\cos^{-1}(-\frac{\sqrt{3}}{2})\)Negative values of cosines occur in the Second and Third Quadrant.
Reference angles are always on the x-axis.
Since we know that cos 30 is √3/2, then the value of the angles is 30 degrees.
The first angle must be subtracted from 180 degrees as shown above.
That's 180 - 30 = 150
The second angle must be added to 180 degrees as also shown above.
That's 180 + 30 = 210

What is the area of the triangle?

Answers
1/2 x 4 x 3 = 6 units squared
Simplify the Expression with Distribution
-10(-8f+1)-8(6f-4)
Answers
Answer: 35f+22
Step-by-step explanation: