Suppose f(x) is a degree three polynomial with ⋅ a root of multiplicity 2 at x=1⋅ a root of multiplicity 1 at x=−2⋅ a y-intercept at (0,4).Find a formula for f(x).
Answers
Since x=1 is a root of multiplicity 2 and x= -2 is a root with multiplicity 1, our polynomial has the form
\(f(x)=A\cdot(x-1)^2\cdot(x+2)\)where A is an unknown constant.
We can find A by substituting into our last result the given point (0,4), that is,
\(4=A\cdot(0-1)^2\cdot(0+2)\)which gives
\(\begin{gathered} 4=A\cdot(-1)^2\cdot2 \\ \text{then} \\ 4=A\cdot1\cdot2 \\ so \\ 4=2A \end{gathered}\)then, by dividing both sides by 2, we get
\(A=2\)Therefore, the answer is:
\(f(x)=2(x-1)^2(x+2)\)Related Questions
if we scale this figure by 600% , what will be the new side length
Answers
Answer:
3 if 2d, 2 if 3D
I think have an amazing day and stay safe and stay home
i need help please :)
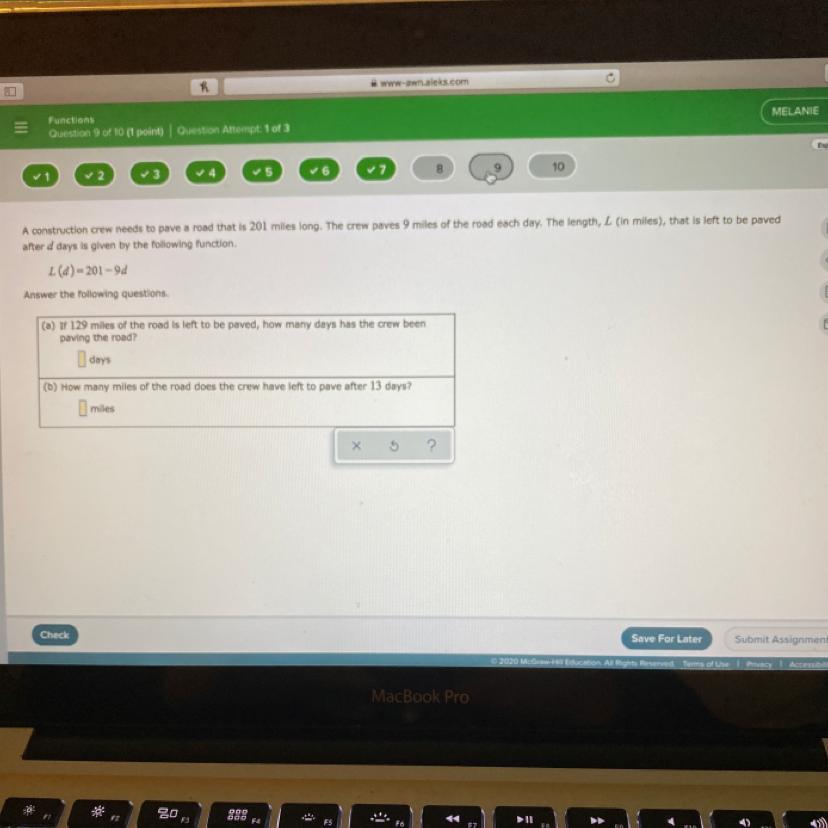
Answers
Answer:
a) 8 days
b) 84 miles
Step-by-step explanation:
a) L (d) = 201 - 9d
9d = 201 - L (d)
9d = 201 - 129
9d = 72
9d/9 = 72/9
d = 8
b) L (d) = 201 - 9d
L (13) = 201 - 9 (13)
= 201 - 117
= 84
Which expression is equivalent to (a2/3 1/31/22
OA 7/665/6
OB. 44/32/3
Oca1/261/2
C.
OD. a4/361/6
OE.al/361/6

Answers
Answer:
E. a^(1/3)b^(1/6)
Step-by-step explanation:
You want an expression equivalent to (a^(2/3)b^(1/3))^(1/2).
Rules of exponentsThe applicable rules of exponents are ...
(a^b)^c = a^(bc)
(ab)^c = (a^c)(b^c)
ApplicationThe given expression simplifies to ...
\((a^{2/3}b^{1/3})^{1/2}=a^{(2/3)(1/2)}b^{(1/3)(1/2)}=\boxed{a^{1/3}b^{1/6}}\)
what's meaning of covariance (x,x)= var(x)? I know covariance describes the relationship between x and y and variance tells us how much the vaules of x vary from the mean. I'm really confused. what is relationship between x and x exactly and what do I mean by saying the relationship could be calculated be finding variance of x
Answers
The covariance of two random variables X and Y is defined as
Cov(X, Y) = E[(X - E[X]) (Y - E[Y])]
where E is expectation.
If we replace Y with X, then this reduces to just the variance of X, which is defined as
Var(X) = E[(X - E[X])²]
Of the 10 contestants in a televised quiz competition, 2 were eliminated during this week's show, and 2 more will be eliminated during next week's show
How many groups of 6 remaining contestants are possible a week from now? Assume that the show airs on the same day every week.
28
210
20,160
151,200
Answers
Answer:a) 28
Step-by-step explanation:
10-2=8
8 objects currently 6 placements for next week = 28 combinations of people of who could stay or leave
Answer:
A
Step-by-step explanation:
The answer is the first one: 28 :) Have a good day everyone!
If a = 17, what is 18a - 89 ?
Answers
Answer: 18(a)-89=217
Step-by-step explanation:
If a = 17 then you substitute/replace the a with the 17. Making 18(a) into 18(17). 18(17)= 306 - 89 = 217.
Hope this helped.
Answer:217
Step-by-step explanation:
putting the value of a in the equation.
18×17-89= 217
Write an equation of the line that is parallel to y = 1/2x + 3 and passes through the point (2,-4). A) y = 1/2x-4 - 15 B) y = -2x-4 + 15 C) y = -2x-5 D) y = 1/2x - 5
Answers
Answer:
D
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = \(\frac{1}{2}\) x + 3 ← is in slope- intercept form
with slope m = \(\frac{1}{2}\)
• Parallel lines have equal slopes , then
y = \(\frac{1}{2}\) x + c ← is the partial equation
to find c substitute (2, - 4 ) into the partial equation
- 4 = \(\frac{1}{2}\) (2) + c = 1 + c ( subtract 1 from both sides )
- 5 = c
y = \(\frac{1}{2}\) x - 5 ← equation of parallel line
You are offered a job in sales where you can choose to
either make a salary $500 (constant) every week or
commission of $20 per sale. Write 2 equations that
represent this scenario and solve the system (find two equations)

Answers
The linear equation for the first scenario is y = 500 while for the second scenario is y = 20x
The equation of a straight line is given by:
y = mx + b;
where y,x are variables, m is the slope of the line and b is the y intercept.
let x represent the number of sales and y represent the total salary for a weeks.
For scenario 1, there is a constant salary of $500. The linear equation becomes:
y = 500
For scenario 2, there is a commission of $20 per sale. The linear equation becomes:
y = 20x
Bookwork code: N84
Look at the poster below showing the price of pencils in a stationery shop.
Annabel wants to buy exactly 76 pencils. What is the lowest amount she can
pay?
Give your answer in pounds (£).
spar
..
Pencils for sale!
30p each
Pack of 10
pencils for £2
Answers
Based on mathematical operations, the lowest amount that Annabel can pay for pencils is $15.20
How is the lowest amount determined?The lowest amount that Annabel can pay for pencils can be determined using the mathematical operations of multiplication and division.
Multiplication and division are two of the four basic mathematical operations, including addition and subtraction.
If Annabel chooses to purchase the first pencil at 30p each, she would pay £22.80 (£0.30 x 76).
If Annabel chooses to purchase the second pencil class of a pack of 10 pencils for £2, she would pay £15.20 [£2 x (76 ÷ 10)].
Pencils for sale
30p each
Pack of 10 pencils for £2
Thus, if Annabel wants to buy the pencils, she can either pay £15.20 or £22.80, but using mathematical operations, the lowest amount she can pay is £15.20.
Learn more about mathematical operations at https://brainly.com/question/4721701.
#SPJ1
Please answer 15 points if answered !

Answers
Answer:
c) 108
Step-by-step explanation:
All angles of a regular polygon are the same.
Have a nice day
LMNP is a rectangle. Find the value of x and the length of each diagonal.
LN=13x-9 and MP=4x+5
Answers
Answer:
x = 3.25 Each diagonal = 34.25. Step-by-step explanation: LMNP is a rectangle and it has diagonals LN and MP. Now, given that LN = 13x - 8 and MP = 9x + 5 Now, we know that the two diagonals of a rectangle are of the same length. So, LN = MP ⇒ 13x - 8 = 9x + 5 ⇒ 4x = 13 ⇒ x = 3.25 (Answer) Therefore, the each diagonal is of (13 × 3.25 - 8) = 35.25 length. (Answer)
Read more at Answer.Ya.Guru – https://answer-ya.com/questions/4694576-lmnp-is-a-rectangle-find-the-value-of-x-and-the-length-of-each.html
Step-by-step explanation:
Answer:
Can you provide an Attachment?
Step-by-step explanation:
^^
can I get an answer please

Answers
Answer:
the second one I'm pretty sure
Step-by-step explanation:
Answer:
its definitely B
Step-by-step explanation:
Use the drawing tool(s) to form the correct answer on the provided graph.
Graph the solution to this system of inequalities in the coordinate plane.
3y > 2x + 12
2x + y < -5
Please respond asap
Answers
Answer:
Hope this helps
Step-by-step explanation:

Find the slope for this question please

Answers
to get the slope of any straight line we only need two points off of it, hmmm let's use the points in the picture below.
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{4}~,~\stackrel{y_2}{8}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{run} {\underset{x_2}{4}-\underset{x_1}{2}}}\implies \cfrac{4}{2}\implies 2\)

A university is interested in determining the average statistics anxiety score for all undergraduate students in the U.S. For a random sample of 33 undergraduate students, it is found that the average average statistics anxiety score is 39.4 with a standard deviation of 0.9. Assume that the statistics anxiety scores for all undergraduate students in the U.S is normally distributed. A 98% confidence interval for the true mean statistics anxiety score μ is closest to.
Answers
The 98% confidence interval for the true mean statistics anxiety score (μ) is approximately (39.037, 39.763).
To calculate the 98% confidence interval for the true mean statistics anxiety score (μ) for all undergraduate students in the U.S., we can use the formula:
Confidence interval = sample mean ± (critical value * standard error)
First, we need to find the critical value associated with a 98% confidence level. Since we are assuming a normal distribution, we can use the Z-table or a statistical software to find this value. For a 98% confidence level, the critical value is approximately 2.33.
Next, we calculate the standard error (SE) using the formula:
SE = standard deviation / √sample size
In this case, the standard deviation is 0.9 and the sample size is 33. Plugging these values into the formula, we get: SE = 0.9 / √33 ≈ 0.156
Now, we can calculate the confidence interval:Confidence interval = 39.4 ± (2.33 * 0.156)
Simplifying the expression:Confidence interval ≈ 39.4 ± 0.363
This gives us the interval (39.037, 39.763). This means we are 98% confident that the true mean statistics anxiety score for all undergraduate students in the U.S. falls within this interval.
for more search question interval
https://brainly.com/question/20309162
#SPJ8
help neeeddded........

Answers
Answer:
D 7a - 11b
Step-by-step explanation:
9a- b -2a - 10b
7a - b -10b
7a - 11b
Answer:
I believe the correct answer is D.
Step-by-step explanation:
Please can anybody help me with this? A card is randomly selected from a standard 52-card deck. What is the probability of picking a club OR a face card? Answer needs to be in decimal form rounded to two decimal places.
Answers
Answer:
0.42
Step-by-step explanation:
To solve the problem, we need to add the probability of picking a club to the probability of picking a face card, and then subtract the probability of picking a club that is also a face card (because we would have counted it twice).
There are 13 clubs in a standard deck, so the probability of picking a club is 13/52 or 0.25.
There are 12 face cards (4 jacks, 4 queens, and 4 kings) in a standard deck, so the probability of picking a face card is 12/52 or 0.23.
However, there are 3 cards that are both clubs and face cards (the jack of clubs, queen of clubs, and king of clubs), so we need to subtract the probability of picking one of those cards. There are 3 of them out of 52 total cards, so the probability of picking a club that is also a face card is 3/52 or 0.06.
Therefore, the probability of picking a club OR a face card is:
0.25 + 0.23 - 0.06 = 0.42 (rounded to two decimal places).
So the answer is 0.42.
Determine the slope of line with points located at (-3,2) and (I. 2).
Answers
We are given the following two points
\((-3,2)\: \text{and}\: (1,2)\)Let us find the slope of the line that passes through these points
The slope of a line is given by
\(m=\frac{y_2−y_1}{ x_2−x_1}\)\(\text{where}\: (x_1,y_1)=(-3,2)\: \text{and}\: (x_2,y_2)=(1,2)\)Let us substitute the given points into the above slope formula
\(m=\frac{2-2}{1-(-3)}=\frac{0}{1+3}=0\)Therefore, the slope of this line is 0.
This means that it is a horizontal line.

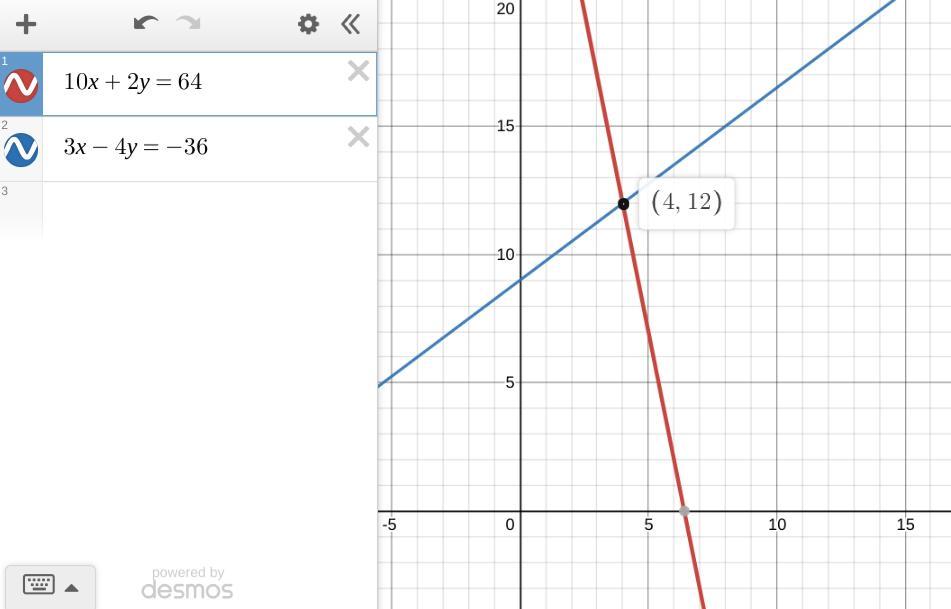
Use the elimination method to solve the system of equations. Choose the
correct ordered pair.
10x+2y=64
3x - 4y = -36
O A. (4, 12)
B. (2,10)
o
C. (-5,8)
O D. (-3, 11)
Answers
9514 1404 393
Answer:
A. (4, 12)
Step-by-step explanation:
Adding the second equation to twice the first will eliminate y.
2(10x +2y) +(3x -4y) = 2(64) +(-36)
23x = 92 . . . . . . . . simplify
x = 4 . . . . . . . . . divide by 23
This value matches choice A: (4, 12).
The graph below shows the relationship between the number of months different students practiced boxing and the number of matches they won:
The title of the graph is Boxing Matches. On x axis, the label is Number of Months of Practice. On y axis, the label is Number of Matches Won. The scale on the y axis is from 0 to 21 at increments of 3, and the scale on the x axis is from 0 to 12 at increments of 2. The points plotted on the graph are the ordered pairs 0, 3 and 1, 6 and 2, 7 and 3, 9 and 4, 11 and 5, 13 and 6, 14 and 7, 16 and 8, 17 and 9, 18 and 10,20. A straight line is drawn joining the ordered pairs 0, 4 and 2, 7.1 and 4, 11 and 6, 13.5 and 8, 17 and 10, 20.5.
Part A: What is the approximate y-intercept of the line of best fit and what does it represent? (5 points)
Part B: Write the equation for the line of best fit in the slope-intercept form and use it to predict the number of matches that could be won after 13 months of practice. Show your work and include the points used to calculate the slope. (5 points)
Answers
Answer:
(a) y intercept is approximately 4.3
(b) \(y = 1.5x+4.5\)
Step-by-step explanation:
Given
See attachment for graph
Solving (a) The y intercept
This is the point where \(x =0\)
From the attached graph; By observation
\(y \approx 4.3\) when \(x =0\)
So, the y intercept is approximately 4.3
Solving (b): The equation of best fit.
First, calculate the slope of the line using:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
Where
\((x_1,y_1) = (9,18)\)
\((x_2,y_2) = (8,16.5)\)
So:
\(m = \frac{16.5- 18}{8 - 9}\)
\(m = \frac{-1.5}{- 1}\)
\(m = 1.5\)
The equation is then calculated using:
\(y =m(x - x_1) + y_1\)
Where: \(m = 1.5\) and \((x_1,y_1) = (9,18)\)
\(y = 1.5(x - 9) + 18\)
\(y = 1.5x - 9*1.5 + 18\)
\(y = 1.5x - 13.5 + 18\)
\(y = 1.5x+4.5\)

find the value of 2xy+3yz-xyz, when x=2, y=-2, z=4
Answers
Answer:
-16
Step-by-step explanation:
2xy + 3yz - xyz
x = 2, y = -2, z = 4
First, plug these values into the equation.
2(2)(-2) + 3(-2)(4) - (2)(-2)(4) = ?
Next, multiply the parentheses.
(-8) + (-24) - (-16) = ?
When you add a negative, you are actually subtracting the number. And when you subtract a negative, you are actually adding the number. Apply this to the equation.
-8 - 24 + 16 = ?
Now, simplify from left to right.
-32 + 16
-16
Your answer is -16.
Hope this helps!
Amy is driving a racecar. The table below gives the distance D (t) (in meters) she has driven at a few times t (in seconds) after she starts.
Find the average rate of change for the distance driven from zero seconds to four seconds.
Find the average rate of change for the distance driven from six seconds to ten seconds.

Answers
(a) 41.6m/sec is the average rate of change for the distance driven from zero seconds to four seconds.
(b) 16.7 m/sec is the average rate of change for the distance driven from six seconds to ten seconds.
Given,
In the question:
Amy is driving a racecar. The table below gives the distance D (t) (in meters) she has driven at a few times t (in seconds) after she starts.
To see the table in the figure.
Now, According to the question:
(a) To find the average rate of change for the distance driven from zero seconds to four seconds.
According to the table we can get t(0 ~ 4 seconds) the average rate
\(V_{a}\) = 166.4 ÷ 4
= 41.6 m/sec
(b) To find the average rate of change for the distance driven from six seconds to ten seconds.
\(V_{b}\) = (239.6 - 172.8) ÷ (10 - 6)
\(V_{b}\) = 66.8 ÷ 4
\(V_{b}\) = 16.7 meters per seconds.
Speed is equal to distance divided by time .
Hence, (a) 41.6m/sec is the average rate of change for the distance driven from zero seconds to four seconds.
(b) 16.7 m/sec is the average rate of change for the distance driven from six seconds to ten seconds.
Learn more about Average Rate at:
https://brainly.com/question/23715190
#SPJ1
ANSWER ASAPPP PLSSS. ILL MARK BRAINLIEST TOO
A scientist is studying the growth of a particular species of plant. He writes the following equation to show the height of the plant f(n), in cm, after n days:
f(n) = 10(1.02)n
Part A: When the scientist concluded his study, the height of the plant was approximately 11.04 cm. What is a reasonable domain to plot the growth function? (4 points)
Part B: What does the y-intercept of the graph of the function f(n) represent? (2 points)
Part C: What is the average rate of change of the function f(n) from n = 1 to n = 5, and what does it represent? (4 points)
Answers
Answer:
Step-by-step explanation:
11.04 = 10(1.02)^n
1.104 = 1.02^n
ln 1.104 = ln 1.02^n
ln 1.104 = n ln 1.02
n = ln 1.104/ ln 1.02
n = 4.99630409516
4.99 can be rounded to 5.
So a reasonable domain would be 0 ≤ x < 5
PART B)
f(0) = 10(1.02)^0
f(0) = 10(1)
f(0) = 10
The y-intercept represents the height of the plant when they began the experiment.
f(1) = 10(1.02)^1
f(1) = 10(1.02)
f(1) = 10.2
(1, 10.2)
f(5) = 10(1.02)^5
f(5) = 10(1.1040808)
f(5) = 11.040808
f(1)=10(1.02)^1
f(1)=10.2
Average rate= (fn2-fn1)/(n2-n1)
=11.04-10.2/(5-1)
=0.22
the average rate of change of the function f(n) from n = 1 to n = 5 is 0.22.
Answer:
Part A
The domain should be 0 ≤n≤5
Part B
f(n) = 10(1.02)^n
The function is in the form y =a b^x where a is the y intercept
The y intercept is 10. This is the value when n =0 days.
Part C
The average rate of growth over the 4 days is .21 cm per day
Step-by-step explanation:
f(n) = 10(1.02)^n
Part A
Let f(n) = 11.04
11.04 = 10 * 1.02 ^n
Divide each side by 10
11.04/10 = 1.02^n
1.104 = 1.02^n
Taking the log of each side
log 1.104 = log 1.02^n
We know log a^b = b log a
log 1.104 = n log 1.02
log 1.104 / log 1.02 = n
4.99630=n
Rounding n to 5
The domain should be 0 ≤n≤5
Part B
f(n) = 10(1.02)^n
The function is in the form y =a b^x where a is the y intercept
The y intercept is 10. This is the value when n =0 days.
Part C
To find the average rate of change
f(5) - f(1)
-----------
5-1
f(5) = 11.04
f(1) = 10 *1.02 =10.2
11.04 - 10.2
-----------
5-1
.84
-----
4
.21 cm per day
The average rate of growth over the 4 days is .21 cm per day
You have a combination lock
with 3 secret digits. Find the 3
correct digits using the
following clues and enter your
answer below.
127 One digit is right and in its place
138 One digit is right, but in the wrong place
791
Two digits are right but both are in the
wrong place
452 All digits are wrong
8
529 One digit is right, but in the wrong place
Answers
Answer:
987
Step-by-step explanation:
You want to determine a three-digit combination based on clues about which digits are right and/or correctly placed.
Clue 1This tells you one of digits 1, 2, or 7 is correct and correctly placed.
Clue 2 tells you that digit is not 1. Clue 4 tells you that digit is not 2.
7 is correctly placed as the 3rd digit
Clue 2We already know that 1 is not the correct digit. This means 3 must be the first digit, or 8 must be the first or second digit.
Clue 3We already know that 7 is a correct digit, properly placed as the 3rd digit. Since 1 is not a correct digit, 9 must be a correct digit, properly placed as the 1st digit.
9 is correctly placed as the 1st digit
Combining this fact with Clue 2 means ...
8 is correctly placed as the 2nd digit
The combination is 987.
__
Check
Clues 4 and 5 are consistent with this combination.
Find angle a in the taper shown,x = 9.342 inchesy = 6.692 inchesz = 2.952 inches

Answers
We need to find angle a in the figure.
We know that:
x = 9.342 inches
y = 6.692 inches
z = 2.952 inches
We can do so by finding the legs in the following triangle:
The adjacent leg is x. And the opposite leg is found by subtracting z from y, and then dividing the result by two (assuming the figure is symmetric):
\(\frac{y-z}{2}\)Thus, we have:
\(\begin{gathered} \sin a=\frac{\text{ opposite leg}}{\text{ adjacent leg}} \\ \\ \sin a=\frac{\frac{y-z}{2}}{x} \\ \\ \sin a=\frac{\frac{6.692-2.952}{2}}{9.342} \\ \\ \sin a=\frac{1.87}{9.342} \\ \\ a=\arcsin\left(\frac{1.87}{9.342}\right) \\ \\ a\cong11.55\degree \end{gathered}\)
Write the factors of \( {a}^{3} + {b}^{3} .\)
Answers
Step-by-step explanation:
\(a {}^{3} + b {}^{3} \)
Notice how that for both a and b are raised to an odd power. This means we can factor this by a binomial raised to an odd power.
Let divide this by
\(a + b\)
Since that is also a odd power.
\(( {a}^{3} + {b}^{3} ) \div (a + b)\)
We get
a quotient of
\(( {a}^{2} - ab + {b}^{2} )\)
So our factors are
\((a + b)( {a}^{2} - ab + {b}^{2} )\)
Answer:
\((a+b)(a^{2} -ab+b^{2} )\)
Step-by-step explanation:
\(\textbf{We need to factor this expression}\) \(\textbf{by applying the sum of two cubes rule:}\)
\(\Longrightarrow\) \(A^{3} +B^{3} =(A+B)(A^{2} -AB+B^{2} )\)
Here,
A= a
B= b
So, \((a+b)(a^{2} -ab+b^{2} )\)
\(\leadsto\leadsto\leadsto\leadsto\leadsto\leadsto\leadsto\leadsto\leadsto\leadsto\)
\(\textsl{OAmalOHopeO}\)
Find 30th term of the arithmetic sequence, given that the first few terms are given by
6,12,18,..
Answers
Answer:
180
Step-by-step explanation:
Considering that it is counting by 6's, just multiply 6 by 30 to get the 30th term of the sequence
What is a dot plot and how do you read it? Check all that apply. O A dot plot displays data values as dots number line. O Dot plots show the frequency with which a specific item appears in a data set. There was 1 run in 5 of the games. I There were 0 runs in 2 of the games. O Dot plots show the distribution of the data. There were a total of 19 games.

Answers
Answer:
the first third and 5th one i think, check my answer first XD
Step-by-step explanation:
Which expression is equivalent to (3 squared) Superscript negative 2?
Answers
Answer:
–81
Step-by-step explanation:
Your research of competitors shows prices of $45, $78, $13, $125, and $66. If you throw out the
highest and lowest data points (outliers), what is the mean of the remaining prices?
Answers
Answer:
1. 63 or
2. 37.8
step-by-step explanation:
1. $125,$78, $66, $45, $13 take out $125 and $13 then add $78, $66, $45 and you get $189 then divided by 3 and you $63
2.$125,$78, $66, $45, $13 take out $125 and $13 then add $78, $66, $45 and you get $189 then divided by 5 and you $37.8
Answer:
ITS 63
Step-by-step explanation:
JUST DID DA TEST CUZ