Suppose that 2 were subtracted from each of the values in a data set that
originally had a standard deviation of 7.5. What would be the standard
deviation of the resulting data?
A. 2
B. 7.5
C. 9.5
O D. 5.5
Answers
Answer:
Option B. 7.5 is the correct answer
Step-by-step explanation:
Let us define standard deviation first.
Standard deviation is the square root of variance. Standard Deviation tells us that how far are the values in a data set from the mean.
Now, if a constant is subtracted from all values of a dataset, the standard deviation remains the same. Only the origin or mean of the data changes by subtracting a constant from whole data set.
Given that the standard deviation of dataset is 7.5
Subtracting 2 from each value of dataset will not change the standard deviation as 2 is a constant.
Hence,
Option B. 7.5 is the correct answer
Answer:
7.5 it stays the same
Step-by-step explanation:
Related Questions
lol bro help me :((((((((((((((((((((((((((((((
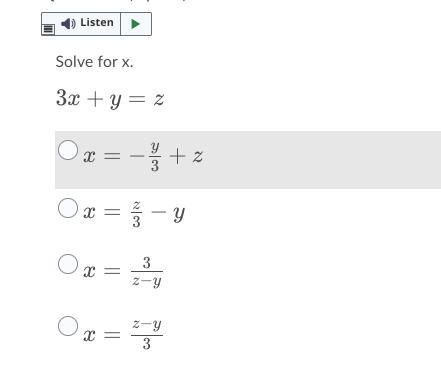
Answers
Answer:
The choice four ;
\(x = \frac{z - y}{3} \)
Step-by-step explanation:
\(3x + y = z \\ 3x = z - y \\ x = \frac{z - y}{3} \)
Which expression represents seven less than the product of thirteen times a number, and two squared?
(13x + 22) · 7
7(13x · 22)
7 + 13x + 22
7 + 13x · 22
(13x · 22) − 7
Answers
Seven less than the product of thirteen times a number, and two squared is as follows;
(13x × 2²) - 7
How to represent an expression?The expression says seven less than the product of thirteen times a number, and two squared.
Let
the number = x
Hence, the product of thirteen times a number, and two squared is as follows:
13(x)(2²)
Therefore, seven less than the product of thirteen times a number, and two squared is as follows;
(13x × 2²) - 7
learn more on expression here: https://brainly.com/question/14172188
#SPJ1
State where in the ty-plane the hypotheses of the Existence and Uniqueness Theorem are satisfied for the equation y'=(ycot(2t))/(t^2+y^2+1)
Answers
We can conclude that the hypotheses of the Existence and Uniqueness Theorem are satisfied in any rectangular region in the ty-plane that does not contain the curve t² + y² = -1.
Where in the ty-plane the hypotheses of the existence and uniqueness theorem are satisfiedThe Existence and Uniqueness Theorem for first-order ordinary differential equations states that if a differential equation of the form y' = f(t, y) satisfies the following conditions in some rectangular region in the ty-plane:
1. f(t, y) is continuous in the region.
2. f(t, y) satisfies a Lipschitz condition in y in the region, i.e., there exists a constant L > 0 such that |f(t, y₁) - f(t, y₂)| ≤ L|y₁ - y₂| for all t and y₁, y₂ in the region.
then there exists a unique solution to the differential equation that passes through any point in the region.
In the case of the differential equation y' = (y cot(2t)) / (t² + y² + 1), we have:
f(t, y) = (y cot(2t)) / (t² + y² + 1)
This function is continuous everywhere except at the points where t² + y² + 1 = 0, which is the curve t² + y² = -1 in the ty-plane. Since this curve is not included in any rectangular region, we can say that f(t, y) is continuous in any rectangular region in the ty-plane.
To check if f(t, y) satisfies a Lipschitz condition in y, we can take the partial derivative of f with respect to y and check if it is bounded in any rectangular region. We have:
∂f/∂y = cot(2t) / (t² + y² + 1) - (2y² cot(2t)) / (t² + y² + 1)²
Taking the absolute value and simplifying, we get:
|∂f/∂y| = |cot(2t) / (t² + y² + 1) - (2y² cot(2t)) / (t² + y² + 1)²|
= |cot(2t) / (t² + y² + 1)| * |1 - (2y² / (t² + y² + 1)))|
Since 0 ≤ (2y² / (t² + y² + 1)) ≤ 1 for all t and y, we have:
1/2 ≤ |1 - (2y² / (t² + y² + 1)))| ≤ 1
Also, cot(2t) is bounded in any rectangular region that does not contain the points where cot(2t) is undefined (i.e., where t = (k + 1/2)π for some integer k). Therefore, we can find a constant L > 0 such that |∂f/∂y| ≤ L for all t and y in any rectangular region that does not contain the curve t² + y² = -1.
Learn more on differential equation here;
https://brainly.com/question/1164377
#SPJ1
Answer this for me please

Answers
The function values are f(10) = 198 and g(-6) = 24/7; the range of h(x) is 3/5 < h(x) < 31/25 and the inverse function is p-1(x) = -(1 + 3x)/(5 + x)
Calculating the function valuesGiven that
f(x) = 2x^2 - 2
g(x) = 4x/(x - 1)
So, we have
f(10) = 2(10)^2 - 2 = 198
g(-6) = 4(-6)/(-6 - 1) = 24/7
The range of h(x)Here, we have
h(x) = (7x - 4)/5x
Where
1 < x < 5
So, we have
h(1) = (7(1) - 4)/5(1) = 3/5
h(5) = (7(5) - 4)/5(5) = 31/25
So the range is 3/5 < h(x) < 31/25
The inverse of p(x)Here, we have
P(x) = (5x - 1)/(3 - x)
So, we have
x = (5y - 1)/(3 - y)
This gives
3x - xy = 5y - 1
So, we have
y(5 + x) = -1 - 3x
This gives
y = -(1 + 3x)/(5 + x)
So, the inverse function is p-1(x) = -(1 + 3x)/(5 + x)
Read more about functions at
https://brainly.com/question/28532394
#SPJ1
select all of the factors of x3 5x2 2x 8 x 5 x3 x 4 x 1 x3 x 2
Answers
The all the factors of x³ + 5x² + 2x – 8 are (x+4)(x-1) and (x+2) , the correct options are (c) , (d) and (f) .
In the question ,
it is given that the equation is f(x) = x³ + 5x² + 2x – 8 ,
we have to find the factors of f(x) = x³ + 5x² + 2x – 8 .
We know that ,The Factor Theorem states if (x-t) is a factor of f(x) if and only if f(t)=0 .
So , Option(a) Let g(x) = x + 5 be a factor
that means for x = -5 , f(-5) = (-5)³ + 5(-5)² + 2(-5) – 8 = 2 ≠ 0 ,
hence it is not a factor .
In option (b) Let g(x) = x - 5 be a factor
that means For x = 3 , f(3) = (3)³ + 5(3)² + 2(3) – 8 = 70 ≠ 0 ,
hence it is not a factor .
In option (c) Let g(x) = x + 4 be a factor
that means For x = -4 , the equation is f(-4) = (-4)³ + 5(-4)² + 2(-4) – 8 = 0 ,
hence it is a factor .
In option (d) Let g(x) = x - 1 be a factor
that means For x = 1 , f(1) = (1)³ + 5(1)² + 2(1) – 8 = 0 ,
hence it is a factor .
In option (e) Let g(x) = x + 3 be a factor
that means For x = -3 , it becomes f(-3) = (-3)³ + 5(-3)² + 2(-3) - 8 = 4 ≠ 0 ,
hence it is not a factor .
In option (f) Let g(x) = x + 2 be a factor
that means For x = -2 ,the equation f(-2) = (-2)³ + 5(-2)² + 2(-2) - 8 \(=\) 0 ,
hence it is a factor .
Therefore , the factors are (x+2) , (x - 1) and (x + 4) .
The given question is incomplete , the complete question is
Select all of the factors of x³ + 5x² + 2x – 8.
(a) x + 5
(b) x – 3
(c) x + 4
(d) x – 1
(e) x + 3
(f) x + 2
Learn more about Factors here
https://brainly.com/question/3717180
#SPJ4
In a chess club there are 10 males and 15 females. What percentage of the club is females?
Answers
Answer:
Step-by-step explanation:
Solve equation by factoring n^2=5n-4
Answers
\(\huge\text{Hey there!}\)
\(\huge\textbf{Equation:}\)
\(\mathsf{n^2 = 5n - 4}\)
\(\huge\textbf{Convert:}\)
\(\mathsf{5n - 4 = n^2}\)
\(\huge\textbf{Subtract }\boxed{\bf n^2}\huge\textbf{ to both sides:}\)
\(\mathsf{5x - 4 - n^2 = n^2 - n^2}\)
\(\huge\textbf{Simplify it:}\)
\(\mathsf{-n^2 + 5x - 4 = 0}\)
\(\huge\textbf{Factor the LEFT side of the equation:}\)
\(\mathsf{(-n + 1)\times (n - 4) = 0}\)
\(\huge\textbf{Simplify that as well:}\)
\(\mathsf{-n + 1 = 0 \ or\ even\ \ n - 4 = 0}\)
\(\huge\textbf{Lastly, simplify that as well:}\)
\(\mathsf{n = 1\ or\ n = 4}\)
\(\huge\textbf{Therefore, your answer should be: }\)
\(\huge\boxed{\frak{n = 1\ or \ n = 4}}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
Complete the sentence to describe the triangle shown.
GHI is _____ and _____.
Answers
Can you please help me

Answers
B. (The second one) x ≤ -3
Devante has a lunch account in the school cafeteria His starting balance at the beginning of the month is $35.50. The first wook, Davante bought 3 lunches and his account balance was $28.00. The second week. Devante
bought 5 lunches and his account balance was 515 50
In a model that relates the balance of his lunch account as a function of the number of lunches he buys, what does the rate of change represent?
A: the number of lunches he purchases
B: the starting balance of his lunch account
C: the amount of money in his lunch account
D: the amount of money he pays for each lunch
Answers
Answer:
D the amount of money he pays for each lunch
Step-by-step explanation:
In each lunch Devante has, he pays 2,50 $ according to:
Money in t = t₀ he has 35,50 $ paid 3 lunches and spent
35,50 - 28 = 7,5
Then the cost of each lunch is 7,5 / 3 = 2,5 $
After that
bought 5 lunches and spent 28 - 15,5 = 12,50
Again 12,5 / 5 = 2,5 $
Now the model for the situation is a straight line with a slope 2,5
In an x , y cartesian system in which y is money in the account and x is the number of lunches, such a straight line will be
y = b - m*x ( b the intercept on y and m the negative slope)
y = 35,50 - 2,5*x
So answering the question is lyrics D the amount of money he pays for each lunch
please help it’s due tomorrow
[x + y = -4
[x - y = 2
Answers
Answer:
which one substitution or elimination
Step-by-step explanation:
Substitution: (-1,-3 )
Elimination: (-1,-3)
i hope this helps you :)
Please mark me brainlest
Evaluate the expression if a = 4, b = 9, and c = 1.
3b÷c1−a
–27
–9
9
27
Answers
Answer:
Given - a = 4
b = 9
c = 1
To find - Value of equation
Solution -
3b ÷ c^1 - a
Putting the value of a,b and c in the equation
3(9) ÷ (1)^1 - 4
27 ÷ 1 - 4
27 ÷ (-3)
27 × (1 /(-3)
27/(-3)
(-9)
Answer:
-9
Step-by-step explanation:
Substitute the values into the expression.
= 3(9)÷(1)1-4
evaluate/simplify each part first.
= 27÷1-4
= 27÷(-3)
simplify (positive divided by a negative is a negative)
= -9
which value would make the statement true?
2 4
— > —
? 12
O 4
O 6
O 12
O 24
Pls help guys.
Answers
Answer:
the answer is 6
Step-by-step explanation:
the answer is 6
plz help with this:)

Answers
9514 1404 393
Answer:
-4
Step-by-step explanation:
The point (x, y) = (0, 0) is on the line, so it represents a proportional relation. Any ratio of y to x will be the slope. The choice that makes this computation easiest is ...
x = 1, y = -4
y/x = -4/1 = -4
The slope of the line is -4.
I need this question quick please

Answers
Answer:
First one, second one, fourth one, and last one
Step-by-step explanation:
The hypotenuse of a right triangle is 10 inches long. One of the legs is 2 inches longer than the other one. If x is the length of the shorter leg, what is the equation
Answers
Answer:
The equation is
X²+2x-48 = 0
Shorter one is 6 inches
Other side= 8 inches
Step-by-step explanation:
The equation for a right angle triangle normally is
A² = B² + C²
Where A = hypotenuse
Then B and C are the order sides of the triangle.
This time
Hypotenuse= 10 inches
The shorter one is X
While the other one is X+2
The equation
10²= x² +(x+2)²
100= x² + x² + 4x +4
100 - 4 = 2x² +4x
96= 2x² +4x
48 = x² +2x
X²+2x-48 = 0
Solving for x
X² +8x-6x-48= 0
X(x+8)-6(x+8)=0
(X-6)(x+8)= 0
X= 6 or x= -8
Definitely x is posiy
So x= 6
Shorter one is 6 inches
Other side= 6+2= 8 inches
Acontinous random variable X has a pdf given by p(x) = (5x4 0≤x≤1 0, otherwise) Let Y=X3. Find the probability distribution function
Answers
I'll use the method of transformations.
If \(f_X(x)\) denotes the PDF of \(X\), and \(y=g(x)=x^3 \iff x=g^{-1}(y) = y^{1/3}\), we have
\(f_Y(y) = f_X\left(g^{-1}(y)\right) \left|\dfrac{dg^{-1}}{dy}\right|\)
\(\dfrac{dg^{-1}}{dy} = \dfrac13 y^{-2/3}\)
\(\implies f_Y(y) = f_X\left(y^{1/3}\right) \left|\dfrac13 y^{-2/3}\right| = \boxed{\begin{cases} \dfrac53 y^{2/3} & \text{if } 0 \le y \le 1 \\ 0 & \text{otherwise} \end{cases}}\)
For what value of A is the function, (x), continuous at x=0?

Answers
(i) \(\lim_{x \to \frac{\pi^-}{2}}\) h(x) = 3
(ii) \(\lim_{x \to \frac{\pi^+}{2}}\) h(x) = -1
(iii) h(0) = 1/7
The value of λ must be 7, for h(x) to be continuous at x = 0.
The given function is,
h(x) = 1/7, when x = 0
= 1 - 2 cos 2x, when x < π/2
= 1 + 2 cos 2x, when x > π/2
= x cos x/sin λx, when x < 0
Now,
(i) \(\lim_{x \to \frac{\pi^-}{2}}\) h(x) = \(\lim_{x \to \frac{\pi^-}{2}}\) (1 - 2 cos 2x) = 1 - 2 cos π = 1 + 2 = 3
(ii) \(\lim_{x \to \frac{\pi^+}{2}}\) h(x) = \(\lim_{x \to \frac{\pi^+}{2}}\) (1 + 2 cos 2x) = 1 + 2 cos π = 1 - 2 = -1
(iii) h(0) = 1/7
Since the function is continuous at x = 0, so
\(\lim_{x \to 0}\) h(x) = h(0)
\(\lim_{x \to 0}\) x cos x/sin λx = 1/7
\(\lim_{x \to 0}\) cos x.\(\lim_{x \to 0}\) 1/λ(sinλx/λx) = 1/7
1/λ = 1/7
λ = 7
Hence the value of λ must be 7.
To know more about continuous here
https://brainly.com/question/30089268
#SPJ1
Is 6 inches in 10 seconds proportional to 12 inches in 60 seconds?
Answers
Answer: No
Step-by-step explanation:
to be proportional, both numbers have to increase by the same number
because if u multiply 6 by 2 you get 12, but when you multiply 10 by 2 you get 20, not 60 it would be proportional if you said 6 and 10 in to 12 and 20 in
.What is the probability of two 6 sided diced rolled, adding up to lucky 13
Answers
Answer:
0
Step-by-step explanation:
Assuming the six sided dice are numbered 1 through six
The max each could roll is 6
6+6 = 12
They cannot reach a sum of 13
Find the first two equations that are needed to solve the following story problem: How many milliliters of a 5% acid solution and how many milliliters of a 17% acid solution must be mixed to obtain 60 mL of a 13% acid solution?
Answers
Answer:
Step-by-step explanation:
saw it on chegg
.05x+.17y=.13
x+y=60
The two correct equations are "\(0.05 x+0.17 y=0.13\) and \(x+y=60\)". A further solution is provided below.
According to the question,
Let,
Quantity of 5% acid solution will be "x".Quantity of 17% acid solution will be "y".Given total acid solution,
= 60 mL
then,
→ \(x+y = 60\)...(equation 1)
We know that the concentration of mixture = 13%
hence,
→ \(5 \ percent \ of \ x + 17 \ percent \ of \ y =13 \ percent (x+y)\)
or,
→ \(0.05x+0.17y=0.13(60)\)
Thus the above answer is correct.
Learn more:
https://brainly.com/question/259604
The table shows the height of a softball that Hallie threw in the air. Is the relationship shown linear? Why or why not?

Answers
Answer:
No
Step-by-step explanation:
Because .5 = 7.2
So 1 = 14.4
What is the slope of the line shown below

Answers
Answer:
Option:C 2/3
Equation= y=2/3x-5
Answer:
2/3
Step-by-step explanation:
to find slope m, use this method
m=(y2-y1)/(z2-x1)
therefore m=(1-(-7))/((9-(-3))
m=8/12.
m=2/3
The dot plot shows the height, in feet, of a group of trees being studied. How many trees are being studied? Enter the answer in the box.

Answers
Answer:
13
Step-by-step explanation:
By counting the amount of dots there is on the graph you would end up with 13 trees.
an election ballot asks voters to select three city commissioners from a group of twelve candidates. in how many ways can this be done?
Answers
Answer:
Step-by-step explanation:
Since order does not matter \(_{12}C_3\\ \\ \frac{12!}{3!9!}\\ \\ 220\)
For each value of u determine whether it is a solution to -2u-6<-20
Answers
Answer:
u > 7
Step-by-step explanation:
-2u -6 < -20 Add 6 to both sides
-2u - 6 + 6 < -20 + 6
-2u < -14 Divide both sides by -2. When you multiply or divide both sides by a negative number, you must flig the sign.
\(\frac{-2u}{-2}\) > \(\frac{-14}{-2}\)
u > 7
Helping in the name of Jesus.
The answer is:
u > 7
In-depth explanation:
You haven't told me what the values of u are, but I'll solve the equation for u.
Add 6 on each side:
\(\bf{-2u-6 < -20}\)
\(\bf{-2u < -14}\)
Divide each side by -1 and reverse the sign:
\(\bf{2u > 14}\)
Now divide each side by 2
\(\bf{u > 7}\)
what is 1/10 to the 3rd power.
Answers
Answer: 0.001
Step-by-step explanation:
15. Find the volume of a rectangular prism with the following dimensions.a length of 11 cm, a width of 4.2 cm, and a height of 7.1 cm.3308.24 cm3328.02 cm322.3 cm346.2 cm
Answers
For this problem, we are given the dimensions of a rectangular prism and are asked to determine its volume.
The volume of a rectangular prism is given by the product of the three dimensions, therefore we have:
\(\begin{gathered} V=\text{ height}\cdot\text{ length}\cdot\text{ width}\\ \\ V=11\cdot4.2\cdot7.1=328.02\text{ cubic cm} \\ \end{gathered}\)The correct answer is 328.02 cubic centimeters.
In a recent year, the scores for the reading portion of a test were normally distributed, with a mean of and a standard deviation of . Complete parts (a) through (d) below. (a) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is less than . The probability of a student scoring less than is nothing. (Round to four decimal places as needed.) (b) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is between and . The probability of a student scoring between and is nothing. (Round to four decimal places as needed.) (c) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is more than . The probability of a student scoring more than is nothing. (Round to four decimal places as needed.) (d) Identify any unusual events. Explain your reasoning. Choose the correct answer below. A. than 0.05. B. than 0.05. C. The event in part is unusual because its probability is less than 0.05. D. The events in parts are unusual because its probabilities are less than 0.05.
Answers
The question is incomplete. Here is the complete question.
In a recent year, the socres for the reading portion of a test were normally distributed, with a mean of 23.3 and a standard deviation of 6.4. Complete parts (a) through (d) below.
(a) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is less than 18. (Round to 4 decimal places as needed.)
(b) Find a probability that a random selected high school student who took the reading portion of the test has a score that is between 19.9 and 26.7.
(c) Find a probability that a random selected high school student who took the reading portion of the test ahs a score that is more than 36.4.
(d) Identify any unusual events. Explain your reasoning.
Answer: (a) P(X<18) = 0.2033
(b) P(19.9<X<26.7) = 0.4505
(c) P(X>36.4) = 0.0202
(d) Unusual event: P(X>36.4)
Step-by-step explanation: First, determine the z-score by calculating:
\(z = \frac{x-\mu}{\sigma}\)
Then, use z-score table to determine the values.
(a) x = 18
\(z = \frac{18-23.3}{6.4}\)
z = -0.83
P(X<18) = P(z< -0.83)
P(X<18) = 0.2033
(b) x=19.9 and x=26.7
\(z = \frac{19.9-23.3}{6.4}\)
z = -0.67
\(z = \frac{26.7-23.3}{6.4}\)
z = 0.53
P(19.9<X<26.7) = P(z<0.53) - P(z< -0.67)
P(19.9<X<26.7) = 0.7019 - 0.2514
P(19.9<X<26.7) = 0.4505
(c) x=36.4
\(z = \frac{36.4-23.3}{6.4}\)
z = 2.05
P(X>36.4) = P(z>2.05) = 1 - P(z<2.05)
P(X>36.4) = 1 - 0.9798
P(X>36.4) = 0.0202
(d) Events are unusual if probability is less than 5% or 0.05. So, part (c) has an unusual event.
The probability will be:
(a) 0.2038
(b) 0.4046
(c) 0.0203
(d) Event in part (c) is unusual.
According to the question,
\(\mu = 23.2\)\(\sigma = 6.4\)Let,
"X" shows the test scores.(a)
The z-score for X=18 will be:
→ \(z = \frac{X- \mu}{\sigma}\)
\(= \frac{18-23.3}{6.4}\)
\(= -0.828\)
So,
The probability will be:
→ \(P(X<18) = P(z < -0.828)\)
\(= 0.2038\)
(b)
The z-score for X=19.9 will be:
→ \(z = \frac{X -\mu}{\sigma}\)
\(= \frac{19.9-23.3}{6.4}\)
\(= -0.531\)
The z-score for X=26.7 will be:
→ \(z = \frac{X -\mu}{\sigma}\)
\(= \frac{26.7-23.3}{6.4}\)
\(= 0.531\)
So,
The probability will be:
→ \(P(19.9 < X< 23.3) = P(-0.531 < z< 0.531)\)
\(= 0.4046\)
(c)
The z-score for X=36.4 will be:
→ \(z = \frac{X -\mu}{\sigma}\)
\(= \frac{36.4-23.3}{6.4}\)
\(= 2.047\)
So,
The probability will be:
→ \(P(X > 36.4 )= P(z > 2.047)\)
\(= 0.0203\)
(d)
Just because it's probability value is less than 0.05, so that the events is "part c" is unusual.
Learn more about probability here:
https://brainly.com/question/23044118
The Happy Widget Company has a fixed cost of $1,163 each day to run their factory and a variable cost of $1.69 for each widget they produce.
Create a linear model for their daily cost.
How much does it cost them to produce 288 widgets?
Round your answer to the nearest cent.
Answers
Final answer: 486.72 dollars
HOPE THIS HELPS