Suppose that for a function g (x), g (4) = 7. Select all of the statements that are true.
A. 4 is in the range of g.
B. For a value a, it is possible that g (a) = 4.
C. For a value y, it is possible that g (4) = y.
D. The point (4,7) is on the graph of y = g (x).
E. The point (7,4) is on the graph y = g (x).

Answers
Answer:
B and D
Step-by-step explanation:
The wording in the answer choices make a huge difference. It is possible implies that there is a possibility
A is false. The range of a function is the output value of the function for the input value in the domain of the function. So we can say with certainty that 7 is in the range since it is an output. But we cannot state that 4 is in the range because we have only one output value 7 for g(4)
A good example is a constant function such as g(x) = 7. Here, whatever the value of x, the y value is always 7. This represents a horizontal line passing through y = 7. So the range is just a single number {7}
B can be true. It is possible but not a certainty that f(a) = 4 for some value of a. For example, consider the function g(x) = x + 3.
At x = 4, g(4) = 4 .1 + 3 = 7
At x = 1, g(1) = 1 + 3 = 4 so it is possible for 4 to be an output
C is false. A well-defined function has only a unique value for a specific input of x. So we cannot get two different values for a single x value.
D is true. Since at x =4, y = g(x) = 7, this corresponds to a point on the graph. The point will be (x=4, y =7) or (4,7)
E is false. The x, y coordinates have been interchanged in this answer choice
The true statements are B and D.
The wording in the answer choices make a huge difference.
It is possible implies that there is a possibility
A. 4 is in the range of g.
A is false.
The range of a function is the output value of the function for the input value in the domain of the function. So we can say with certainty that 7 is in the range since it is an output. But we cannot state that 4 is in the range because we have only one output value 7 for g(4)
A good example is a constant function such as g(x) = 7.
Here, whatever the value of x, the y value is always 7.
This represents a horizontal line passing through y = 7.
So the range is just a single number {7}
B. For a value a, it is possible that g (a) = 4.
B can be true.
It is possible but not a certainty that f(a) = 4 for some value of a.
For example, consider the function g(x) = x + 3.
At x = 4, g(4) = 4 .1 + 3 = 7
At x = 1, g(1) = 1 + 3 = 4 so it is possible for 4 to be an output.
C. For a value y, it is possible that g (4) = y.
C is false.
A well-defined function has only a unique value for a specific input of x. So we cannot get two different values for a single x value.
D. The point (4,7) is on the graph of y = g (x).
D is true.
Since at x =4, y = g(x) = 7, this corresponds to a point on the graph.
The point will be (x=4, y =7) or (4,7)
E. The point (7, 4) is on the graph y = g(x).
False. The statement doesn't provide any information about g(7), and we cannot determine whether the point (7, 4) lies on the graph of the function y = g(x) based solely on the given information.
To learn more on function click:
https://brainly.com/question/29204088
#SPJ7
Related Questions
Really in need of help :( please !
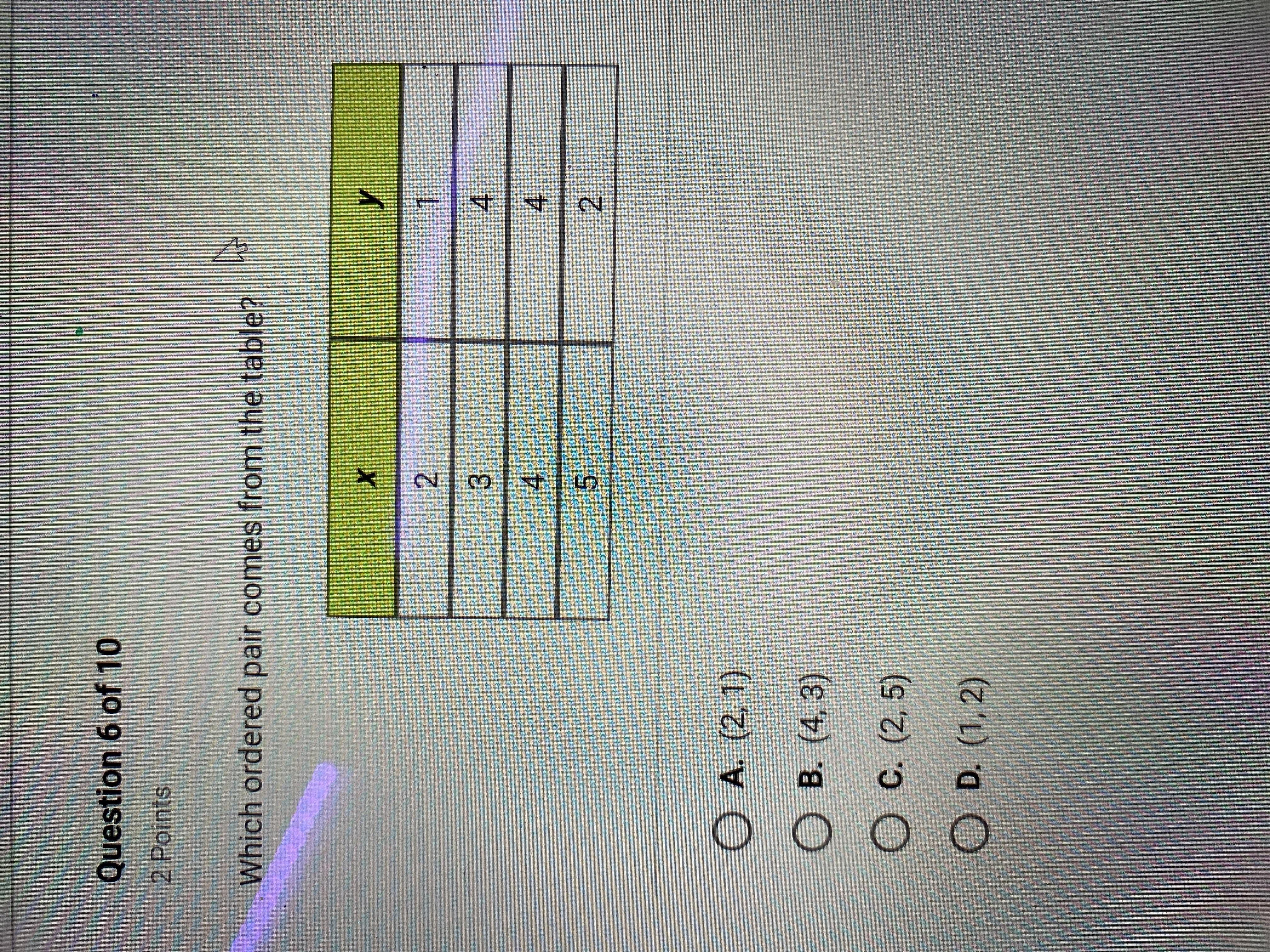
Answers
Answer:
A
Step-by-step explanation:
(2,1) - only one in the table. Remember (x,y)
he entire graph of the function is shown in the figure below.
Write the domain and range of using interval notation.
Someone please help me. I really nee help. this question is due tonight before 8 and im stuck.

Answers
The given graph shows that the function is periodic and fluctuates between y = -2 and y = 2. So, the range of the function is [-2,2].
The graph covers one period, which is from x = -3 to x = 3, and then repeats itself indefinitely in both directions. So, the domain of the function is (-∞, ∞).
In general, the domain of a function consists of all the possible input values that the function can take. In this case, since the function repeats itself indefinitely, it can take any input value from negative infinity to positive infinity.
So, the domain is (-∞, ∞). The range of a function, on the other hand, consists of all the possible output values that the function can produce.
In this case, the function oscillates between y = -2 and y = 2, so the range is [-2,2]. The interval notation for the domain is (-∞, ∞) and for the range is [-2,2].
for such more questions on function
https://brainly.com/question/11624077
#SPJ8
which combinations hold the same amount of liquid as an 8-pint bowl
Answers
1 quart = 32 fl oz
1 pt = 16 oz
Using these conversions you will multiply the number of quarts or pints by the number of ounces in each and then add the totals together to find if they equal 128 oz.
C. 4 x 32 = 128 oz
D. 2 x 32 + 8 x 8 = 128 oz
E. 3 x 32 + 2 x 16 = 128 oz
Given the following sets, find the set (A U B) n (AUC).
U= {1, 2, 3, ..., 10}
A=(2, 5, 7, 10}
B = {1, 2, 3)
C={1, 2, 3, 4, 5}
Answers
The set (A U B) n (A U C) is {2, 5, 7, 10}. A.
To find the set (A U B) n (A U C), we first need to calculate the union of sets A and B, and then calculate the union of that result with set C. Finally, we find the intersection of these two sets.
Set A U B:
The union of sets A and B, denoted as A U B, is the combination of all elements from both sets without any repetitions.
A contains the elements 2, 5, 7, and 10, while B contains the elements 1, 2, and 3.
A U B consists of the elements {1, 2, 3, 5, 7, 10}.
Set (A U B) U C:
Next, we calculate the union of the set (A U B) with set C, denoted as (A U B) U C. A U B contains the elements {1, 2, 3, 5, 7, 10} and C contains the elements {1, 2, 3, 4, 5}.
Taking the union of these two sets results in {1, 2, 3, 4, 5, 7, 10}.
Finding the intersection:
Finally, we find the intersection of (A U B) U C with A U C. A U C consists of the elements {2, 5, 7, 10}.
The intersection of these two sets is the combination of common elements.
The common elements are {2, 5, 7, 10}.
For similar questions on set
https://brainly.com/question/13458417
#SPJ8
Your firm purchases a business copier that costs $14,000 and requires $3,000 in maintenance for each year of its four-year life. After four years, the copier will be replaced. The copier falls into the MACRS three-year class life category. Use table 12.8 on page 415 in your textbook for DDB depreciation. If the tax rate is 32 percent, whats the depreciation tax shield for this project in year 4?
Answers
Answer:
The depreciation tax shield for this project in year 4 is $178.24.
Explanation:
To calculate the depreciation tax shield for this project in year 4, we need to first determine the depreciation expense for year 4 using the MACRS three-year class life category and the double-declining balance (DDB) method.
From Table 12.8 on page 415 of the textbook, we can see that the depreciation rate for year 1 is 33.33%, for year 2 it is 44.45%, for year 3 it is 14.81%, and for year 4 it is 7.41%.
Using the DDB method, we can calculate the depreciation expense for each year as follows:
Year 1: Depreciation expense = $14,000 x 33.33% = $4,667
Year 2: Depreciation expense = ($14,000 - $4,667) x 44.45% = $3,554
Year 3: Depreciation expense = ($14,000 - $4,667 - $3,554) x 14.81% = $830
Year 4: Depreciation expense = ($14,000 - $4,667 - $3,554 - $830) x 7.41% = $557
The total depreciation expense over the four years is the sum of the individual year's depreciation expenses, which is:
$4,667 + $3,554 + $830 + $557 = $9,608
Now, we can calculate the depreciation tax shield in year 4. The depreciation tax shield is the amount of the depreciation expense that reduces the firm's taxable income, multiplied by the tax rate. In year 4, the depreciation tax shield is:
Depreciation tax shield = Depreciation expense in year 4 x Tax rate
Depreciation tax shield = $557 x 32% = $178.24
Therefore, the depreciation tax shield for this project in year 4 is $178.24.
Learn more about Double-Declining Balance on:
brainly.com/question/24296752
U thought this was a professional answer?!!!!??????
You're wrong!!!!!!!!!!!!!!!!!
But the answer is correct though...
:))
PEW PEW PEW
Bing Chilling
It's over...
No more to read
Happy birthday if it's ur birthday...
Have a nice day my king:)
ASAPP PLEAASSEE!!!
Nathan deposits $940 every 2 months into his daughter's RESP. If the account earns 3.99% / annual, compound quarterly, how much will be in the account after 25 years?
Answers
There will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
To calculate the amount in Nathan's daughter's RESP after 25 years, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = Final amount (amount in the account after 25 years)
P = Principal amount (amount deposited every 2 months)
r = Annual interest rate (in decimal form)
n = Number of times the interest is compounded per year
t = Number of years
In this case, Nathan deposits $940 every 2 months, so the principal amount (P) is $940. The annual interest rate (r) is 3.99% or 0.0399 in decimal form. Since the interest is compounded quarterly, the compounding frequency (n) is 4. The number of years (t) is 25.
Since Nathan deposits every 2 months, we need to calculate the total number of deposits made over 25 years. There are 12 months in a year, so in 25 years, there will be 25 * 12 = 300 months. However, since Nathan deposits every 2 months, the number of deposits (m) is 300 / 2 = 150.
Now, we can substitute these values into the formula:
A = 940(1 + 0.0399/4)^(4*25)
Calculating the exponent first:
(1 + 0.0399/4)^(4*25) ≈ 2.703236
Now, substituting the calculated exponent and the number of deposits into the formula:
A = 940 * 2.703236 * 150 ≈ $594,311.34
Therefore, there will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
It's important to note that this calculation assumes Nathan makes the same $940 deposit every 2 months consistently over the 25-year period and does not make any withdrawals from the account during that time. Additionally, the actual amount may vary slightly due to rounding and any potential changes in interest rates over the years.
For more such questions on compounded visit:
https://brainly.com/question/24274034
#SPJ8
at the movies three candy bars and two sodas cost $14.00. Four candy bars and three sodas cos $19.50. How much is the soda?
Answers
The cost of a soda is $2.50. By solving the system of equations formed from the given information, the value of S is determined to be 2.50.
To find the cost of the soda, let's set up a system of equations using the given information. Let's assume the cost of a candy bar is represented by 'C' and the cost of a soda is represented by 'S.'
From the first statement, we can write the equation:
3C + 2S = 14.00 ----(Equation 1)
From the second statement, we can write the equation:
4C + 3S = 19.50 ----(Equation 2)
To solve the system of equations, we can use a method called substitution. Rearranging Equation 1, we get:
S = (14.00 - 3C) / 2
Substituting this expression for S into Equation 2, we have:
4C + 3((14.00 - 3C) / 2) = 19.50
Simplifying this equation, we get:
4C + (42.00 - 9C) / 2 = 19.50
8C + 42.00 - 9C = 39.00
-C + 42.00 = 39.00
-C = 39.00 - 42.00
-C = -3.00
C = 3.00
Now we can substitute the value of C back into Equation 1 to find the value of S:
3(3.00) + 2S = 14.00
9.00 + 2S = 14.00
2S = 14.00 - 9.00
2S = 5.00
S = 5.00 / 2
S = 2.50
Therefore, the cost of a soda is $2.50.
For more such questions on soda
https://brainly.com/question/28624529
#SPJ8
Determine whether the series is convergent. Identify the type of the series and test used to evaluate.

Answers
The first series,
\(\displaystyle \sum_{k=2}^\infty \frac{\cos(k)}{k^2}\)
is convergent. By comparison, using the fact that |cos(x)| ≤ 1 for all real x,
\(\displaystyle \sum_{k=2}^\infty \frac{\cos(k)}{k^2} \le \sum_{k=2}^\infty \frac1{k^2}\)
and the bounding series is a convergent p-series (with p = 2).
The second series,
\(\displaystyle \sum_{k=2}^\infty \frac{e^k}{\left(2+\frac1k\right)^k}\)
is divergent by the limit test. We have
\(\dfrac{e^k}{\left(2 + \frac1k\right)^k} = \dfrac{e^k}{2^k\left(1+\frac1{2k}\right)^k} = \left(\dfrac e2\right)^k \cdot \dfrac1{\left(1+\frac1{2k}\right)^k}\)
By definition,
\(e = \displaystyle \lim_{k\to\infty}\left(1+\frac1k\right)^k\)
so that
\(\displaystyle \lim_{k\to\infty}\left(1+\frac1{2k}\right)^k = \lim_{k\to\infty}\sqrt{\left(1+\frac1{2k}\right)^{2k}} = \sqrt{\lim_{k'\to\infty}\left(1+\frac1{k'}\right)^{k'}} = \sqrt{e}\)
so that the limit of the summand is
\(\displaystyle \lim_{k\to\infty} \frac{e^k}{\left(2+\frac1k\right)^k} = \frac1{\sqrt{e}} \lim_{k\to\infty} \left(\frac e2\right)^k\)
but e > 2, so the limit is ∞.
What is the perimeter, in feet, of a rectangle whose length is four times its width
which is 8 feet?
Answers
Step by step
We know perimeter is
P = 2L + 2W
We know L = 4W
We know W = 8
Substitute these into our formula and solve
P = 2(4 x 8) + 2(8)
P = 2(32) + 16
P = 64 + 16
P = 80 ft
Problem solved!
How many terms are in the expression? 9a + 6b + 3c + 1 A) 1 B) 2 C) 3 D) 4
Answers
Answer:
D.) there is 9a and 6b ,3c and 1 thats four different terms
Step-by-step explanation:
Have a nice day! :D
Benny has 72 teddy bears at his toy store. He wants to put them on 8 shelves with
the same number of bears on each shelf. How many teddy bears are on each shelf?
Answers
Answer: Answer below
Step-by-step explanation: So you would simply have to divide 8 into 72 which would be 9.
we can verify our answer by doing 9x8 which equals 72.
Answer: 9
Step-by-step explanation:
bears divided by shelves = number of bears per shelf
72 bears divided by 8 shelves= 9 bears per shelf
\(\frac{2}{2+\sqrt{7} }\)
Answers
Answer:
\(\huge\boxed{\sf \frac{2\sqrt{7}-4 }{3}}\)
Step-by-step explanation:
This is a rationalizing denominator question.
Given expression:\(= \displaystyle \frac{2}{2+\sqrt{7} } \\\\Multiply \ and \ divide \ by \ conjugate \ 2 - \sqrt{7} \\\\= \frac{2}{2+\sqrt{7} } \times \frac{2-\sqrt{7} }{2-\sqrt{7} } \\\\\underline{\sf Using \ formula:}(a+b)(a-b)=a^2-b^2\\\\= \frac{2(2-\sqrt{7}) }{(2)^2-(\sqrt{7})^2 } \\\\= \frac{4-2\sqrt{7} }{4-7} \\\\= \frac{4-2\sqrt{7} }{-3} \\\\= \frac{-(4-2\sqrt{7}) }{3} \\\\= \frac{2\sqrt{7}-4 }{3} \\\\\rule[225]{225}{2}\)
what complex number has an absolute value of 5 ?
Answers
Answer:
the absolute value of -5 is 5, and the absolute value of 5 is also 5. ∣ a + b i ∣ = a 2 + b 2 . |a+bi| = \sqrt{a^2 +b^2}
please give me heart
A bottle contains 30 fluid Ounces of orange juice and 18 fluid Ounces of pineapple Juice. Whichgraph has a slope that best represents the ratio of orange juice to pineapple juice in thisbottle?

Answers
Explanation:
The ratio of orange juice to pineapple juice is:
\(r=\frac{\text{orange juice}}{\text{ pineapple juice}}=\frac{30}{18}=\frac{5}{3}\)And the function can be written as:
\(\text{orange juice}=\frac{5}{3}\text{ pineapple juice}\)To choose one graph we have to identify one point in each of them and check if the expression above is true for that point. This chosen point cannot be (0,0).
Answer:
Solve for x
x^2 - 8x = -3
Answers
The solutions for the quadratic equation:
x^2 - 8x = -3
Are:
x = 7.6x = 0.4How to solve the quadratic equation?Here we want to solve the quadratic equation:
x^2 - 8x = -3
First we can move all the terms to the left side so we get:
x^2 - 8x + 3 = 0
Using the quadratic formula (or Bhaskara's formula) we can get the solutions for x as:
\(x = \frac{8 \pm \sqrt{(-8)^2 - 4*¨1*3} }{2*1} \\\\x = \frac{8 \pm 7.2 }{2}\)
Then the two solutions for the quadratic equation are:
x = (8 + 7.2)/2 = 7.6
x = (8 - 7.2)/2 =0.4
Learn more about quadratic equations by reading:
https://brainly.com/question/1214333
#SPJ1
3. What is the median of this data set

Answers
Explanation: Median means the middle of the data set. 3 & 4 are the middle. When two numbers are in the middle, you add them then divide by 2.
Factor: x2 – 49 49 = 0 Don't put any space between the two binomials
Answers
The factors of the expression x^2 - 49 = 0 are as follows
(x + 7) (x - 7) = 0
The number 49 is a perfect square, and therefore the roots are either a negative 7 or a positive 7.
So the factores would be x + 7 or x - 7. That is,
When x + 7 = 0
Then x = -7
When x - 7 = 0
Then x = 7
The factors of the expression therefore are
(x + 7) and (x - 7)
This simple question does not require any statistical calculations, only statistical knowledge. The showerhead heights at a men’s athletic locker room were designed to be 72 inches which is well above the mean height of 69.5”. The heights of the athletes are normally distributed. From the choices listed below, which is more likely to be true: a, b or c?
a.The mean height for a randomly selected sample of 20 players is more than 72 inches.
b.The height of one randomly selected player is more than 72 inches.
c.Both a and b are equally likely.
Why? (Justify your answer with a short answer.)
Answers
That both a and b are equally likely, is also not true since the Probability of option b is higher than that of option a.
Option b is more likely to be true. This is because the given information states that the showerhead heights were designed to be 72 inches, which is well above the mean height of 69.5 inches. Therefore, it is reasonable to assume that the majority of the players' heights are below 72 inches. Since the heights of the athletes are normally distributed, the probability of selecting a player at random with a height above 72 inches is relatively low. On the other hand, option a suggests that the mean height of a sample of 20 players is more than 72 inches, which is less likely than option b. Option c, which suggests that both a and b are equally likely, is also not true since the probability of option b is higher than that of option a.
To know more about Probability .
https://brainly.com/question/13604758
#SPJ11
i dont know what is 100x100 is
Answers
Answer:
100x100=10,000
A short and easy trick is to multiply only the first number since the rest are zero. So, multiply 1 and 1: 1 x 1. What do you get? 1, of course. Then, add the rest of the zero's after that. In 100, there are two zero's. In 100, there are two zero's. What is two plus two? Well: 2 + 2 = 4 so, four zero's. After that, add the 4 zero's after the 1. One is extremely important in this problem. 1, one zero, 10, two zero's, 100, three zero's, 1,000, and finally, four zero's, 10,000. So, the trick is to multiply the one by the other one, get 1, and add the zero's in the other numbers. This can work as long as it is something like: 10 x 10, 100 x 100, 1,000 x 1,000, or even beyond. Just remember to add the zero's!
Note: This only works with digits similar to the ones listed below.
Notice that they all have a 1 at the front and zero('s) behind them.
1) 10 x 10
2) 100 x 100
3) 1,000 x 1,000
This can continue to over 100 zero's per digit!
The solution to the expression is A = 10000
Given data ,
Let the expression be represented as A
Now , the value of A is
Let the first number be represented as p
The value of p = 100
Let the second number be represented as q
The value of q = 100
So, A = pq
On simplifying the equation , we get
A = p multiplied by the value of q
And , A = 100 x 100
A = 10000
Therefore , the value of A is 10000
Hence , the expression is A = 10000
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ6
Translate the following phrase into an algebraic expression. Do not simplify. Use the variable names "x" or "y" to describe the unknowns.
the product of two numbers divided by 5
Answers
Step-by-step explanation:
xy/5
.........
....................
The table shows the number of
flowers used to create bouquets,
based on the number of bouquets.
Bouquets
Flowers
Bouquets Flowers
3. 27
5 45
8i 72
Answers
According to the table given, the rate of change is of 9.
The rate of change is given by the change in the output divided by the change in the input.
In this problem:
The input is the number of bouquets.The output is the number of flowers.Taking two of the points, (3,27) and (5,45), we have that:
\(m = \frac{45 - 27}{5 - 3} = \frac{18}{2} = 9\)
Hence, the rate of change is of 9, which would be verified taking any pair of two points.
You can learn more about rate of change at https://brainly.com/question/25823744
To rent a certain meeting room, a college charges a reservation fee of $39 and an additional fee of $6.80 per hour. The chemistry club wants to spend at most
S73.00 on renting the meeting room.
What are the possible amounts of time for which they could rent the meeting room?
Use r for the number of hours the meeting room is rented, and solve your inequality for t.
Answers
1. The possible amounts of time for which the chemistry club could rent the meeting room are 1 to 5 hours.
2. Solving the inequality for t is 39 + 6.80t ≤ 73, where the maximum time is 5 hours.
What is inequality?Inequality is a mathematical statement that two or more mathematical expressions are unequal.
Inequalities are depicted using the following symbols:
Greater than (>)Greater than or equal to (≥)Less than (<)Less than or equal to (≤)Not equal to (≠).The total budget of the chemistry club for renting a meeting room = $73.60
The reservation fee charged by the college = $39
The additional fee (variable cost) per hour = $6.80
The number of hours the club can rent the meeting room = t
The inequality representing the situation is:
39 + 6.80t ≤ 73.
39 + 6.80t ≤ 73
6.8t ≤ 73 - 39
6.8t ≤ 34
t ≤ 5 (34/6.8)
Learn more about inequalities at https://brainly.com/question/24372553.
#SPJ1
Kevin and his elder brother Jason jog every morning. Kevin runs 1.5 miles per hour slower
than Jason. When Jason ran 5 miles, Kevin only ran 4.2 miles. Find their running speeds.
(Write an algebraic equation first, then solve.)
Answers
Answer:
Jason - 9.375 miles per hour
Kevin -7.875 miles per hour
Step-by-step explanation:
Let Jason’s running speed be x miles per hour
Kevin runs 1.5 miles per hour less;
so his running speed will be (x-1.5) miles per hour
At any point, distance = speed * time
Their running time is same here;
Jason’s running time will be 5/x
Kevin’s running time will be 4.2/(x-1.5)
These times are equal;
So;
5/x = 4.2/(x-1.5)
5(x-1.5) = 4.2x
5x - 7.5 = 4.2x
5x-4.2x = 7.5
0.8x = 7.5
x = 7.5/0.8
x = 9.375 miles per hour
So kevin’s speed will be 9.375 - 1.5 = 7.875 miles per hour
6 x (12-2) + 2 to the power of 2
Answers
Answer:
84x
Step-by-step explanation:
Select the correct answer.
Each statement describes a transformation of the graph of f(x) = x. Which statement correctly describes the graph of g(x) if g(x) = f(x - 11)?
A. It is the graph of f(x) where the slope is increased by 11.
It is the graph of f(x) translated 11 units to the left.
It is the graph of f(x) translated 11 units up.
It is the graph of f(x) translated 11 units to the right.
B.
C.
OD.
Answers
The correct answer is C. It is the graph of f(x) translated 11 units to the left.
The correct answer is:
C. It is the graph of f(x) translated 11 units to the left.
When we have a function of the form g(x) = f(x - a), it represents a horizontal translation of the graph of f(x) by 'a' units to the right if 'a' is positive and to the left if 'a' is negative.
In this case, g(x) = f(x - 11), which means that the graph of f(x) is being translated 11 units to the right. However, the answer options do not include this specific transformation. The closest option is option C, which states that the graph of g(x) is translated 11 units to the left.
The graph of f(x) = x is a straight line passing through the origin with a slope of 1. If we apply the transformation g(x) = f(x - 11), it means that we are shifting the graph of f(x) 11 units to the right. This results in a new function g(x) that has the same shape and slope as f(x), but is shifted to the right by 11 units.
Therefore, the correct answer is C. It is the graph of f(x) translated 11 units to the left.
for more such question on graph visit
https://brainly.com/question/19040584
#SPJ8
Which sequence of transformations was applied to the parent tangent function to create the function m(x) = 2tan(3x+4)
Answers
The function m(x) = 2tan(3x+4) is obtained by applying a sequence of transformations to the parent tangent function.
To determine the sequence of transformations, let's break down the given function:
1. Inside the tangent function, we have the expression (3x+4). This represents a horizontal compression and translation.
2. The coefficient 3 in front of x causes the function to compress horizontally by a factor of 1/3. This means that the period of the function is shortened to one-third of the parent tangent function's period.
3. The constant term 4 inside the parentheses shifts the function horizontally to the left by 4 units. So, the graph of the function is shifted to the left by 4 units.
4. Outside the tangent function, we have the coefficient 2. This represents a vertical stretch.
5. The coefficient 2 multiplies the output of the tangent function by 2, resulting in a vertical stretch. This means that the graph of the function is stretched vertically by a factor of 2.
In summary, the sequence of transformations applied to the parent tangent function to create the function m(x) = 2tan(3x+4) is a horizontal compression by a factor of 1/3, a horizontal shift to the left by 4 units, and a vertical stretch by a factor of 2.
Example:
Let's consider a point on the parent tangent function, such as (0,0), which lies on the x-axis.
After applying the transformations, the corresponding point on the function m(x) = 2tan(3x+4) would be:
(0,0) -> (0,0) (since there is no vertical shift in this case)
This example helps illustrate the effect of the transformations on the graph of the function.
For more question on expression
https://brainly.com/question/1859113
#SPJ8
What is the value of the smallest element in the range of this relation?

Answers
Answer:
Smallest element in the set of range is -3
Step-by-step explanation:
From the given set of ordered pairs,
x-value of each pair represents the Domain of the relation.
y-value of the pair represents the Range of the relation.
Set of domain:
{0, 1, 2, 3, 4, 5, 6}
Set of Range:
{1, 3, 2, 5, 2, -3, 2}
Smallest number in the set of range = -3.
Therefore, smallest element in the set of range is -3.
f(x) = 6^2+12x -7
please answer and explainnnn!

Answers

Answer:
A) \(x=-1\pm\sqrt{\frac{13}{6}}\)
Step-by-step explanation:
\(\displaystyle x=\frac{-12\pm\sqrt{12^2-4(6)(-7)}}{2(6)}\\\\x=\frac{-12\pm\sqrt{144+168}}{12}\\\\x=\frac{-12\pm\sqrt{312}}{12}\\\\x=\frac{-12\pm2\sqrt{78}}{12}\\\\x=-1\pm\frac{\sqrt{78}}{6}\\\\x=-1\pm\sqrt{\frac{78}{36}}\\\\x=-1\pm\sqrt{\frac{13}{6}}\)
Fourteen increased by the number d is the same as 6 times the number d
Answers
Answer: d = 14/5
Step-by-step explanation:
14 + d = 6d
14 = 5d
14/5 = d
Check Work:
14 + (14/5) = 6(14/5)
16.8 = 16.8
M = I1+I₂ 31 +32 2 Now let's substitute in our given values. (-2 , 2) = ((-5 Find 2 and y2 We will now set up two equations to solve for our two unknowns of x2 and y₂. (-5 X2 (-5+₂) -5+22), (7+)) 2 - +₂)/2 = We will first want to multiply by 2 on both sides and will get −5+₂= -4 Adding 5 to both sides we get = 7 This is the coordinate of point B. Now we will set up the equation to solve for y2 +y2)/2 =
Answers
The coordinates of point B are (-3, 17).
The given equation is M = I₁ + I₂ = 31 + 32.
Now let's substitute in our given values:
(-2, 2) = ((-5 + x₂) / 2, (-5 + 2 + y₂) / 2)
We will now set up two equations to solve for our two unknowns, x₂ and y₂:
Equation 1: (-5 + x₂) / 2 = -4
Multiply both sides by 2:
-5 + x₂ = -8
Add 5 to both sides:
x₂ = -3
This gives us the x-coordinate of point B.
Equation 2: (-5 + 2 + y₂) / 2 = 7
Simplify:
(-3 + y₂) / 2 = 7
Multiply both sides by 2:
-3 + y₂ = 14
Add 3 to both sides:
y₂ = 17
This gives us the y-coordinate of point B.
Therefore, the coordinates of point B are (-3, 17).
For more such questions on coordinates
https://brainly.com/question/29660530
#SPJ8