Tell whether the given number is a solution of each question. ( Must show work for credit)
1. 9 = 2a + 3; 3
2. 5n - (-30) = 5; 7
3. 4.4r - 2.8 = 1.6; 1
Answers
Answer/Step-by-step explanation:
1. \( 9 = 2a + 3 \) ; 3
Let's solve for a.
\( 9 - 3 = 2a \) (subtraction property of equality)
\( 6 = 2a \)
\( \frac{6}{2} = a \) (division property of equality)
\( 3 = a \)
\( a = 3 \)
Therefore, 3 is a solution to 9 = 2a + 3
2. \( 5n - (-30) = 5 \) ; 7
\( 5n + 30 = 5 \) (- × - = +)
\( 5n = 5 - 30 \) (Subtraction property of equality)
\( 5n = -25 \)
\( \frac{5n}{5} = \frac{-25}{5} \) (division property of equality)
\( n = -5 \)
Therefore, 7 is not a solution of \( 5n - (-30) = 5 \)
3. \( 4.4r - 2.8 = 1.6 \) ; 1
\( 4.4r = 1.6 + 2.8 \)
\( 4.4r = 4.4 \)
\( \frac{4.4r}{4.4} = \frac{4.4}{4.4} \)
\( r = 1 \)
Therefore, 1 is a solution of \( 4.4r - 2.8 = 1.6 \).
Related Questions
Which equations are correct?
Select each correct answer.
6a^5(6a^5)=36a^25
6b^4(−3b^4)=−18b^8
5x^4(4x^2)=20x^6
3z^7(4z^2)=12z^9
Answers
Find two positive real numbers whose product is a maximum.
The sum of the first and three times the second is 42.
Answers
Answer:
21, 7
Step-by-step explanation:
1st number = x, 2nd number = y
Given x + 3y = 42 (1)
find maximum value of xy.
Multiply by x on (1), get
x^2 + 3xy = 42x
3xy = -x^2 + 42x = -(x^2 - 42x)
Make a perfect square,
3xy = -(x^2 - 42x + 21^2) + 21^2
3xy = 21^2 - (x - 21)^2
Note (x - 21)^2 is non-negative, so when x = 21, the right hand side has a maximum value of 21^2, so xy is a maximum.
Use (1) and x = 21, we get 21 + 3y = 42, 3y = 21, y = 7
Hence, the two positive real numbers are 21 and 7
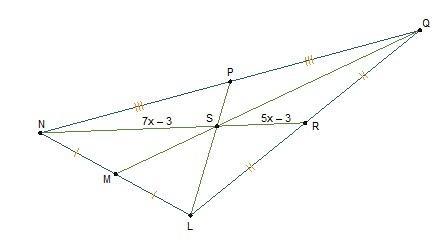
what is the length of segment ns
Answers
Given that x is equal to 1 and S is the centroid of the triangle NLQ, NS will have a length of 4 units.
What is centroid?The centroid of a flat figure or solid figure, also known as the geometric center or center of figure, in mathematics and physics, is the arithmetic mean position of all the points on the figure's surface. Any n-dimensional Euclidean object is included by the same definition. The centroid of a triangle is the location where the triangle's three medians connect. It may alternatively be described as the location where the three medians come together. A line connecting a side's midpoint and the triangle's opposite vertex is called the median.
Here,
We may infer from the centroid's features that it divides each median in a ratio of 2:1.
NS=2SR
7x-3=2(5x-3)
7x-3=10x-6
3x=3
x=1
NS=7x-3
=7*1-3
=4 units
The length of NS will be 4 units as the value of x is 1 and S is the centroid of triangle NLQ.
To know more about centroid,
https://brainly.com/question/10708357
#SPJ4
What is the value of y?

Answers
The vertical value in a pair of coordinates. How far up or down the point is. The Y Coordinate is always written second in an ordered pair of coordinates (x,y) such as (12,5). In this example, the value "5" is the Y Coordinate.
A line has a slope of 2/3 while another line has a slope of -3/2 What can you conclude about the lines
Answers
Answer:
They are perpendicular
Step-by-step explanation:
If 2 slopes are negative reciprocals of each other, it means they are perpendicular
Answer:
The lines are perpendicular because they have opposite reciprocal slopes.
Step-by-step explanation:
During WW! mortars were fired from trenches 3 feet down The mortars had a velocity of 150 ft/s. Determine how long it will take for the mortar shell to strike its target?
Answers
The mortar shell will strike the target in 0.02 seconds
How to find the durationThe duration to strike the target is solved using the formula for velocity which is
= distance / time
The problem gives the distance to be 3 feet and velocity is 150ft/s
therefore
150 = 3 / time
time = 3 / 150
time = 0.02 seconds
Learn more on velocity at:
https://brainly.com/question/25749514
#SPJ1
Janie has $48 in her checking account. If she writes a check for $19, find her new account balance?
Answers
Answer:
48-19=29
$29 is the answer
Step-by-step explanation:
A trucker wanted to track how long it took to reach Bismarck. When she started out, her clock
read 7:00AM. When she refueled, the clock read 8:00AM. After reaching Bismarck, the clock read
10:00AM. How many hours did it take this trucker to reach Bismarck?
Answers
Answer:
Below
Step-by-step explanation:
From 7 to 10 AM is THREE hours (if the times are all on the same day)
A clock has a face in the shape of a circle the distance across a circle is 12 inches what is the area of the clock face in square inches?
Answers
Answer:
18.84 square inches
Step-by-step explanation:
Distance across = diameter. The area formula for circles is A= πr. r in here means radius which is 6 inches (half of diameter). π is generally 3.14 or 22/7 depending on the question. multiply the value of π and 6, then you get the answer.
Write the equation in either slope-intercept or point-slope form for the
line that goes through (1,1) and (3,-5). *
Answers
Answer:
y = mx + b
m = (-5-1)/(3-1)
m = -3
1=(-3)1 + b
b= 4
y= -3x + 4
Ahmad is going to rent a truck for one day. There are two companies he can choose from, and they have the following prices.
Company A charges an initial fee of $55 and an additional 50 cents for every mile driven.
Company B has no iniţial fee but charges 60 cents for every mile driven.
Answers
A linear equation is an algebraic equation of the form \(y=mx+b.\) involving where m is the slope and b is the y-intercept
Company A charges is represented by equation, \(A=55+0.5x\)
Company B charges is represented by equation , \(B=0.6x\)
Let number of miles is represented by x .
\(1 cent= \frac{1}{100}dollar\\\\50cents=\frac{50}{100}=0.5dollar\\\\60 cents=\frac{60}{100}=0.6dollar\)
Since, Company A charges an initial fee of $55 and an additional 50 cents for every mile driven.
So, equation is, \(A=55+0.5x\)
Since, Company B has no initial fee but charges 60 cents for every mile driven.
So, equation is, \(B=0.6x\)
Learn more:
https://brainly.com/question/14304163
Last month, the remaining balance on Sarah's credit card was $457.32. If she adds charges of $74.82 for clothes, $150 for food and $94.79 for car repairs and then makes a payment of $525.00, what is the current balance on the credit card (what does she currently owe)?
Answers
Answer: $ 251.93
Step-by-step explanation:
Calcular los 3/5 de los 2/3 de las 3/4 de 560
Answers
For the fractions, the calculation of 3/5 of 2/3 of 3/4 of 560 is equal to 168.
How to solve fractions?To calculate 3/5 of 2/3 of 3/4 of 560, break it down step by step:
Step 1: Calculate 3/4 of 560:
3/4 × 560 = (3 × 560) / 4 = 1680 / 4 = 420
Step 2: Calculate 2/3 of the result from Step 1:
2/3 × 420 = (2 × 420) / 3 = 840 / 3 = 280
Step 3: Calculate 3/5 of the result from Step 2:
3/5 × 280 = (3 × 280) / 5 = 840 / 5 = 168
Therefore, 3/5 of 2/3 of 3/4 of 560 is equal to 168.
Find out more on fractions here: https://brainly.com/question/78672
#SPJ1
Is (-12,8) a solution to 2x+y=40
Answers
Answer:
no it is not. the line crosses the x in 20, and crosses the y in 40
twice the square of a number
Answers
Answer:
2 * x^2
Step-by-step explanation:
in word form: two times the square of x
"a number" can be any variable; i used x
Answer:
x² × 2
Step-by-step explanation:
Notice vocabulary:
twice → multiplication by a factor of two → ×2a number → unknown number; variable → xthe square → raised to the power of two → x²Put this information together.
"Twice the square of a number"
Since it says of a number, this number comes first → \(x\)
"Twice the square of a number"
The square of a number means that the variable will be squared → \(x^2\)
"Twice the square of a number"
Multiply the variable by a factor of two → \(x^2*2\)
:Done
Question 2 (15 points )
Determine the scale factor from circle A to circle B.
O
Scale factor =
B
30

Answers
Thus, the scale factor from circle A to circle B is found to be 2.
Explain about the scale factor:The ratio between comparable measurements of just an element and a portrayal of that element is known as a scale factor in mathematics. The copy will be larger if the scaling factor is a whole number. A fractional scaling factor means that the duplicate will be smaller.
You must first choose which direction we are scaling in order to determine the scale factor:
Scale Up = larger measurement / smaller measurement (smaller to larger).Smaller measurement equals greater measurement when scaling down.The radius of circle A = 2 units
The radius of circle B = 4 units.
So, there is a dilation with the scale factor of 2 units as 2*2 = 4 units.
Thus, the scale factor from circle A to circle B is found to be 2.
know more about the scale factor:
https://brainly.com/question/25722260
#SPJ1
For what values of theta do maximum r-values occur on the graph the polar equation r = 2 cos4 theta? Note that the maximum r-value occurs at a point that is the maximum distance from the pole
Answers
Answer:r=2 cos^4(theta)
Step-by-step explanation:To find the values of theta where the maximum r-values occur on the graph of the polar equation r = 2 cos^4(theta), we need to find where the derivative of r with respect to theta is equal to zero, since the maximum r-values occur at these points.
First, we can simplify the equation by using the identity cos(2theta) = 2cos^2(theta) - 1 and substituting cos^2(theta) = (1 + cos(2theta))/2. This gives:
r = 2 cos^4(theta) = 2(1/2 + 1/2 cos(2theta))^2 = 1 + cos(2theta) + cos^2(2theta)/2.
Next, we can take the derivative of r with respect to theta, using the chain rule:
dr/dtheta = -sin(2theta) - 2cos(2theta)sin(2theta).
Setting this equal to zero and factoring out sin(2theta), we get:
sin(2theta)(-1 - 2cos(2theta)) = 0.
This equation is satisfied when sin(2theta) = 0 or cos(2theta) = -1/2.
When sin(2theta) = 0, we have 2theta = k*pi for some integer k. Therefore, theta = k*pi/2.
When cos(2theta) = -1/2, we have 2theta = 2*pi/3 + 2*k*pi or 2theta = 4*pi/3 + 2*k*pi for some integer k. Therefore, theta = pi/3 + k*pi or theta = 2*pi/3 + k*pi.
These are the values of theta where the maximum r-values occur on the graph of the polar equation r = 2 cos^4(theta).
y = 2x + 1
2x - y = 3
Answers
The slope of the equations is equal. Then the lines are parallel to each other.
What is a linear equation?A connection between a number of variables results in a linear model when a graph is displayed. The variable will have a degree of one.
The linear equation is given as,
y = mx + c
Where m is the slope of the line and c is the y-intercept of the line.
The linear equation is given below.
y = 2x + 1 ....1
2x - y = 3
y = 2x - 3 ....2
The slope of both equations is 2.
The slope of the equations is equal. Then the lines are parallel to each other.
More about the linear equation link is given below.
https://brainly.com/question/11897796
#SPJ1
5. My sisters were having a
lemonade stand. They
made 2 gallon of
lemonade. If they divided it
equally into 6 cups, how
much lemonade was in
each cup?
Answers
there are 3 cups of lemonade in each cup
4. This diagram is a straightedge and compass construction of a line perpendicular to line AB passing through point C. Which segment has the same length as segment EA.
a. EC
b. ED
C. BE
d. BD

Answers
Answer:
Segment ED has the same length as EA
The line segment which is equal to EA is ED. Therefore, option B is the correct answer.
In the given diagram, a line perpendicular to line AB passes through point C.
What is the tangent to the circle?A tangent to a circle is a line which intersects the circle at only one point. The common point between the tangent and the circle is called the point of contact.
The length of two tangents drawn from an external point to a circle is equal.
From the given figure we can see there are three circles, two large circles and one small circle.
Line segment EA is tangent to a small circle.
The line segment which is equal to EA is ED because ED is another tangent to a small circle from the same external point.
The line segment which is equal to EA is ED. Therefore, option B is the correct answer.
To learn more about the tangent to a circle visit:
https://brainly.com/question/16592747.
#SPJ2
Clarence walks 3.1 miles around Lake Johnson every day for five days.
If it takes him a total of 6 hours to walk the 15.5 miles, what is his
average time per day?
minutes per day.
Answers
Answer:
Average time per day = 1.2 hours per day
Average time per day = 72 minutes per day
Step-by-step explanation:
To find Clarence's average time per day, we need to divide the total time he takes to walk the 15.5 miles by the number of days he walks, which is five.
Let's calculate his average time per day:
Average time per day = Total time / Number of days
Since Clarence takes a total of 6 hours to walk the 15.5 miles, we'll divide 6 by 5 to find his average time per day:
Average time per day = 6 hours / 5
Average time per day = 1.2 hours per day
To convert hours to minutes, we'll multiply the average time per day by 60:
Average time per day = 1.2 hours * 60 minutes
Average time per day = 72 minutes per day
Therefore, Clarence's average time per day is 72 minutes.
A game card handed out at a grocery store states the probabilities of winning a prize: 0.2 for $10, 0.1 for $5, and 0.7 for $0. What is the probability of winning any amount of money?
Answers
Answer:
Step-by-step explanation:
To calculate the probability of winning any amount of money, we need to sum up the probabilities of winning each individual prize.
Given the probabilities stated on the game card:
Probability of winning $10 prize = 0.2
Probability of winning $5 prize = 0.1
Probability of winning $0 prize = 0.7
To find the probability of winning any amount of money, we add these probabilities together:
0.2 + 0.1 + 0.7 = 1
The sum of the probabilities is 1, which indicates that the total probability of winning any amount of money is 1 or 100%.
Therefore, the probability of winning any amount of money in this game is 100%.
Hope this answer your question
Please rate the answer and
mark me ask Brainliest it helps a lot
\(\frac{3}{4}(m+n)-\frac{1}{4}(m-n);m=\frac{1}{2},n=\frac{1}{3}\)
Answers
Answer:
\(\frac{3}{4}(m+n)-\frac{1}{4}(m-n) = \frac{14}{24}\)
Step-by-step explanation:
Given
\(\frac{3}{4}(m+n)-\frac{1}{4}(m-n);m=\frac{1}{2},n=\frac{1}{3}\)
Required
Solve
To do this, we simply substitute values of m and n in the given expression
\(\frac{3}{4}(\frac{1}{2}+\frac{1}{3})-\frac{1}{4}(\frac{1}{2}-\frac{1}{3})\)
Evaluate the brackets
\(\frac{3}{4}(\frac{3 + 2}{6})-\frac{1}{4}(\frac{3-2}{6})\)
\(\frac{3}{4}(\frac{5}{6})-\frac{1}{4}(\frac{1}{6})\)
Open Brackets
\(\frac{15}{24} - \frac{1}{24}\)
Take LCM
\(\frac{15 - 1}{24}\)
\(\frac{14}{24}\)
Hence:
\(\frac{3}{4}(m+n)-\frac{1}{4}(m-n) = \frac{14}{24}\)
An odometer show that a car has traveled 40,000 miles by January 1, 2020. The car travels 16,000 miles each year. Write an equation that represents the number y of miles on the car’s odometer x years after 2020.
y = __
Answers
The equation will be \(y=40000+16000*x\)
How do you resolve a two-variable equation?Solve one of the equations for a particular variable. After that, insert that into the other equation and find the variable there. To find the value for the other variable, enter that value into either equation.
Two variables are used in what kind of equation?Equations come in two varieties: identities and conditional equations. All possible values of the variables result in an identity. Only certain combinations of the variables' values make a conditional equation true. Two expressions joined by the equals symbol ("=") form an equation.
To know more about identities visit:-
brainly.com/question/14681705
#SPJ1
(i) Write the zeroes of the polynomial by using above graph.
(ii)Form a quadratic polynomial for above graph.
(iii)If a,1/a are the zeroes of polynomial 2x² -x +8k, then find the value of k.
please answer
no spam only for darkparadox #darkparadox

Answers
There is no real Value of k that will satisfy the equation 2x² - x + 8k = 0 if a and 1/a are the roots of the polynomial.
(i) Zeroes of the polynomial:
In the graph, we have two points where the curve intersects the x-axis: one is at (-1,0), and the other is at (2,0).The corresponding values of x are -1 and 2, and they are the zeros of the polynomial. Therefore, the zeros of the polynomial are -1 and 2.(ii) Forming the quadratic polynomial:
From the graph, we can observe that the curve intersects the y-axis at the point (0,5), implying that the constant term of the polynomial is 5.
We can use the formula to find the quadratic polynomial if we have two zeros and one constant term. Thus, the quadratic polynomial is given by:(x + 1)(x - 2) = x² - x - 2x + 2 = x² - 3x + 2. Therefore, the quadratic polynomial is x² - 3x + 2.(iii) Value of k if a, 1/a are the zeroes of the polynomial 2x² - x + 8k:
We know that a and 1/a are the zeroes of the polynomial 2x² - x + 8k. Therefore, we can find the sum and product of the roots and use them to determine the value of k.
The sum of the roots is a + 1/a, and their product is a(1/a) = 1. Using the sum and product of the roots, we can write: a + 1/a = 1/2 (1/2 is the coefficient of x)Substituting a with 1/a in the above equation, we get: 1/a + a = 1/2Multiplying both sides of the equation by 2a, we get: 2 + 2a² = a
Simplifying the equation, we get: 2a² - a + 2 = 0Multiplying both sides by 2,
we get: 4a² - 2a + 4 = 0Dividing both sides by 2, we get: 2a² - a + 2 = 0
Using the quadratic formula, we get: a = [1 ± √(1 - 4(2)(2))]/(2(2))
Simplifying, we get: a = [1 ± √(-31)]/4Since the discriminant of the quadratic formula is negative, the roots are imaginary. Therefore, there is no real value of k that will satisfy the equation 2x² - x + 8k = 0 if a and 1/a are the roots of the polynomial.
For more questions on Value .
https://brainly.com/question/843074
#SPJ8
6.789 to the nearest tenth
Answers
Answer:
6.8
Explanation:
Locate and underline the tenth place 7, and look to the right 8.
Like this. 6.789
Then, the digit to the right 8 is 5 or above. So, we add 1 to the tenth place 7. The digits at the right 8 becomes 0, thus we get 6.8 as the answer.
Suppose there is a simple index of two stocks, stock A and stock B. Stock A opens on Monday with 5000 shares at $2.75 per share. Stock B opens on Monday with 3000 shares at $4.30 per share. Stock A opens on Tuesday at $3.10 per share, and stock B opens on Tuesday at $4.85 per share. Both stocks have the same number of shares that they opened with on Monday. What is the rate of change of this simple index over 1 day?
Answers
The rate of change of the simple index over one day is approximately 12.78%.
To calculate the rate of change of the simple index over one day, we need to determine the percent change in the total value of the index between Monday's opening and Tuesday's opening.
On Monday, Stock A has 5000 shares at $2.75 per share, so its total value is:
Total value of Stock A on Monday = 5000 * $2.75 = $13,750
Similarly, on Monday, Stock B has 3000 shares at $4.30 per share, so its total value is:
Total value of Stock B on Monday = 3000 * $4.30 = $12,900
The total value of the index on Monday is the sum of the values of Stock A and Stock B:
Total value of the index on Monday = $13,750 + $12,900 = $26,650
On Tuesday, Stock A opens at $3.10 per share, and Stock B opens at $4.85 per share. Both stocks still have the same number of shares as on Monday.
The total value of Stock A on Tuesday is:
Total value of Stock A on Tuesday = 5000 * $3.10 = $15,500
The total value of Stock B on Tuesday is:
Total value of Stock B on Tuesday = 3000 * $4.85 = $14,550
The total value of the index on Tuesday is the sum of the values of Stock A and Stock B:
Total value of the index on Tuesday = $15,500 + $14,550 = $30,050
To calculate the percent change in the index, we use the formula:
Percent Change = ((New Value - Old Value) / Old Value) * 100
Percent Change = (($30,050 - $26,650) / $26,650) * 100 ≈ 12.78%
For more such question on index. visit :
https://brainly.com/question/15361818
#SPJ8
w/6 = 6/9 Im failing mathhhh helpppp
Answers
Answer:
W = 4
Step-by-step explanation:
4/6 = 6/9
2/3 = 2/3
multiple 2/3 by 2 and you get 4/6
4/6 = 6/9
w= 4
A local grocery store sells frozen fish sticks in packages of 18. If the cost for a package of frozen fish sticks is $1.95, what is the approximate cost per frozen fish stick?
Answers
Answer:
Rounded to the nearest tenth, $.0.11 per fish stick
Step-by-step explanation:
I divided the cost of the fish sticks, $1.95, and how many in each pack, 18, so the answer was 0.10833333333... and that rounded would be $0.11
Hope this Helps
Need help on this!!! Pls help!!!

Answers
a) The mean of the data-set is of 2.
b) The range of the data-set is of 4 units, which is of around 4.3 MADs.
How to obtain the mean of a data-set?The mean of a data-set is obtained as the sum of all observations in the data-set divided by the number of observations in the data-set, which is also called the cardinality of the data-set.
The dot plot shows how often each observation appears in the data-set, hence the mean of the data-set is obtained as follows:
Mean = (1 x 0 + 5 x 1 + 3 x 2 + 5 x 3 + 1 x 4)/(1 + 5 + 3 + 5 + 1)
Mean = 2.
The range is the difference between the largest observation and the smallest, hence:
4 - 0 = 4.
4/0.93 = 4.3 MADs.
More can be learned about the mean of a data-set at brainly.com/question/1156334
#SPJ1