The accompanying table describes probabilities for the California Daily 4 lottery. The player selects four digits with repetition allowed, and the random variable x is the number of digits that match those in the same order that they are drawn (for a "straight bet). Use the range rule of thumb to determine whether 4 matches is a significantly high number of matches. Select the correct choice below and, if necessary, fill in the answer box within your choice or less. Since 4 is greater than this value, 4 matches is not a significantly high number of matches or more. Since 4 is at least as high as this value, 4 matches is a significantly high number of matches OA. Significantly high numbers of matches are (Round to one decimal place as needed.) OB. Significantly high numbers of matches are (Round to one decimal place as needed.) OC. Significantly high numbers of matches are (Round to one decimal place as needed.) OD. Significantly high numbers of matches are (Round to one decimal place as needed.) OE. Not enough information is given. or more. Since 4 is less than this value, 4 matches is not a significantly high number of matches or less. Since 4 is at least as low as this value, 4 matches is a significantly high number of matches. 1 I-lalalalal 1
Answers
The accompanying table describes probabilities for the California Daily 4 lottery. The player selects four digits with repetition allowed, and the random variable x is the number of digits that match those in the same order that they are drawn (for a "straight bet). Since 4 is less than this value, 4 matches is not a significantly high number of matches. Significantly high numbers of matches are (Round to one decimal place as needed.) Not applicable.
Use the range rule of thumb to determine whether 4 matches is a significantly high number of matches:
Given probabilities for the California Daily 4 lottery are:
P (0 matches) = 256/256 = 1.00
P (1 match) = 0/256 = 0.00
P (2 matches) = 0/256 = 0.00
P (3 matches) = 0/256 = 0.00
P (4 matches) = 1/256 ≈ 0.004
Therefore, the probability of having 4 matches is ≈ 0.004.Since there are only five possible values (0, 1, 2, 3, 4) for the random variable x and since the table shows that P(x) = 0 for all values except 0 and 4, then the mean and median for the distribution are both (0 + 4)/2 = 2.
For the given probabilities,
we have,
σ = √(Σ(x - μ)²P(x))
= √(2²(1 - 0)² + 2²(0 - 1)²)
= √8 ≈ 2.83, and therefore the range rule of thumb gives a ballpark estimate of range ≈ 2 × 2.83 = 5.66 (or rounded to 6).
Thus, a number of matches that is higher than 2 standard deviations from the mean would be considered significantly high. 2 standard deviations above the mean is 2 + 2(2.83) ≈ 7.66. Since 4 matches is less than this value, 4 matches is not a significantly high number of matches.
To know more about probabilities refer here:
https://brainly.com/question/29381779#
#SPJ11
Related Questions
3. The sides of a triangular birdcage are consecutive integers. If the perimeter is 114 centimeters, what is the length of each side? Label each side with an expression that represents its length.

Answers
Answer:
Sides of the triangular birdcage are 37 cm, 38 cm, 39 cm.
Step-by-step explanation:
In the given triangular birdcage, sides of the triangle are consecutive integers.
Let sides of the triangle are x, (x + 1), (x + 2) cm.
Perimeter of a triangle = Sum of all sides of the given triangle
114 = x + (x + 1) + (x + 2)
114 = 3x + 3
3x = 111
x = \(\frac{111}{3}\)
x = 37
Therefore, sides of the triangular birdcage are 37 cm, 38 cm, 39 cm.

what type of measurement scale is used for operating system? nominal scale ordinal scale interval scale ratio scale
Answers
We can actually deduce here that the type of measurement scale that is used for operating system is: Nominal scale.
What is nominal scale?A nominal scale is actually known to be a measurement scale whereby numbers are used as “tags” or “labels” only in order to identify, locate or classify an object.
This measurement scale actually deals only with non-numeric variables. It can be used where numbers have no value.
Other measurement scales include:
Ordinal scale Interval scale Ratio scaleLearn more about nominal scale on https://brainly.com/question/13267344
#SPJ1
Simplify.
10y(3x - 7z).
Please answer quick!
Answers
A hot air balloon company charges for evening sunset flights are based on the function y=25x +100, where x is the number of people traveling in the basket (note the baskey capacity limit is 8) and y is the cost of the trip in dollar. What is the base fee for the balloon ride before passengers are figured in? What does the 25 represent? What is the cost for 5 people to fly?
Answers
Answer: 100 dollars before passengers. 25 is the price per person. 225 for 5 people to fly
Step-by-step explanation:
Fencing x-braces are also used to provide support in rectangular fencing. if ab = 6 feet, ad = 2 feet, and mzdae = 65°, find m
Answers
Evaluating all the information thats provided the measure of the angle CEB in the rectangle which is equal to m is 50°.
The parameteres that are given here are:
AB = 6 feet, AD = 2 feet,
Angle DAE = 65°
Our aim to to find the angle CEB which is M, to find that we need to start with measuring the angle EAB.
Therefore the angles at the right angle are:
∠EAB = 90°-∠DAE
We have the information:
∠EAB = 90°- 65°
∠EAB = 25°
The measure of the angle CEB is calulcated by using the formula:
∠CEB= 2 ×∠EAB
After substituting ∠EAB = 25° We get:
∠CEB=2×25
∠CEB=50°
And hence the ∠CEB = M is 50°.
To learn more about angle click here:
brainly.com/question/28451077
#SPJ4
As a result of a court settlement, an accident victim is awarded $1.2 million. The attomey takes one-third of this amount, another third is used for immediate expenses, and the remaining third is used to set up an annuity. What amount will this annuity pay at the beginning of each quarter for the next 5 years if the annuity earns 7.6% compounded quarterly?
Answers
The amount that remains after the attorney's fee and immediate expenses is $1.2 million / 3 = $400,000. This is the amount that will be used to set up the annuity. To calculate the annuity payments, we need to use the formula for the future value of an annuity:
FV = PMT x [(1 + r)^n - 1] / r
Where FV is the future value, PMT is the payment amount, r is the interest rate per period, and n is the number of periods.
In this case, we want to solve for PMT, so we rearrange the formula:
PMT = FV x r / [(1 + r)^n - 1]
Plugging in the values we have:
FV = $400,000
r = 0.019 (7.6% annual rate divided by 4 quarters)
n = 20 (5 years x 4 quarters per year)
PMT = $400,000 x 0.019 / [(1 + 0.019)^20 - 1] = $11,207.88
Therefore, the annuity will pay $11,207.88 at the beginning of each quarter for the next 5 years.
know more about annuity here
https://brainly.com/question/15056567
#SPJ11
What is the equation of a polynomial function, R, with rational coefficients that
have a zero of 4 + √5 and 3i?
Answers
The equation of a polynomial function, R, with rational coefficients will be;
P (x) = x² - (3i + √5 + 4)x + (12 + 3√5) i
What is Quadratic equation?
An algebraic equation with the second degree of the variable is called an Quadratic equation.
Given that;
The zeroes of the polynomial function are;
⇒ 4 + √5 and 3i
Now,
Since, The zeroes of the polynomial function are;
⇒ 4 + √5 and 3i
So, The factor of the polynomial function are;
(x - (4 + √5)) and (x - 3i)
Hence, We can formulate the polynomial function as;
P (x) = (x - (4 + √5)) (x - 3i)
= (x - 4 - √5) (x - 3i)
= x² - 3ix - 4x + 12i - √5x + 3√5i
= x² - (3i + √5 + 4)x + (12 + 3√5) i
Thus, The equation of a polynomial function, R, with rational coefficients will be;
P (x) = x² - (3i + √5 + 4)x + (12 + 3√5) i
Learn more about the quadratic equation visit:
https://brainly.com/question/24334139
#SPJ1
slope = -1/5 and y intercept = 1
Answers
Answer:
x−y+4=8
4x−5+y=0
7x+y=0
OR
6x−3y=12
6x+2y=8
x+6y=5
Step-by-step explanation:
honestly idrk what the question is here but there are some examples as if on a table! Hope this helped!!
Si hace 10 años las edades de Ana y su madre eran 15 y 40, respectivamente, ¿cuál es la razón entre las edades actuales de ambas?
Opciones:
1/2
5/30
3/8
15/40
Answers
Answer:
3:8
Step-by-step explanation:
15:40
Work out the same by simplifying which they both go in 5
then doing that you can get 3/8 Or 3:8.
Hope it helps!
Spanish:
Resuelve lo mismo simplificando lo que ambos van en 5
luego haciendo eso puedes obtener 3/8 o 3: 8.
A local pizza shop has a membership program for frequent buyers. The membership costs $5 per month and members get a discounted price of $1.75 per slice of pizza. Lamonte purchased a membership to this pizza shop. How much would Lamonte have to pay the pizza shop if he bought 20 slices of pizza this month? What would be the monthly cost for x slices of pizza?
monthly cost with 20 slices:
monthly cost with x slices
Answers
Answer:
monthly cost with 20 slices:
5 + (1.75 x 20)
5+35
40
monthly cost with x slices:
1.75x + 5
Hope this helps!
how can I explain Figure 7.10: The three‐point technique
Answers
The three-point technique, also known as the three-point estimation or the PERT (Program Evaluation and Review Technique), is a project management tool used to estimate the duration or effort required for completing a task or project.
What is is used for?It involves estimating three values for a specific task - the optimistic estimate (O), the most likely estimate (M), and the pessimistic estimate (P).
These three estimates are thenused to calculate the expected estimate (E) using the formula: E = (O + 4M + P) / 6.
The three-point technique is important because it provides a more realistic andreliable estimate by considering both best-case and worst-case scenarios, leading to better planning and decision-making in project management.
Learn more about project management tools at:
https://brainly.com/question/27897160
#SPJ1
Use the rectangle to answer the question,= 1 cm2Make an equation to find the area of the rectangle. Move numbers to the lines to show the answer.cm xcmcm24568912151618
Answers
We need to remember that the area of a figure is given in square units. We have these small squares indicating that each of them is equivalent to 1 square centimeter.
Then, we have 5 square centimeters on one side, and then 3 square centimeters on the other side. Then, we need to put:
5 cm x 3 cm = 15 cm^2

Avery a rectangular bathroom mirror is 6 feet wide and 2 feet tall what is a perm perimeter
Answers
Remember that it has 4 sides. That’s the trick in the ?
Need maths help asap I will mark brainpower
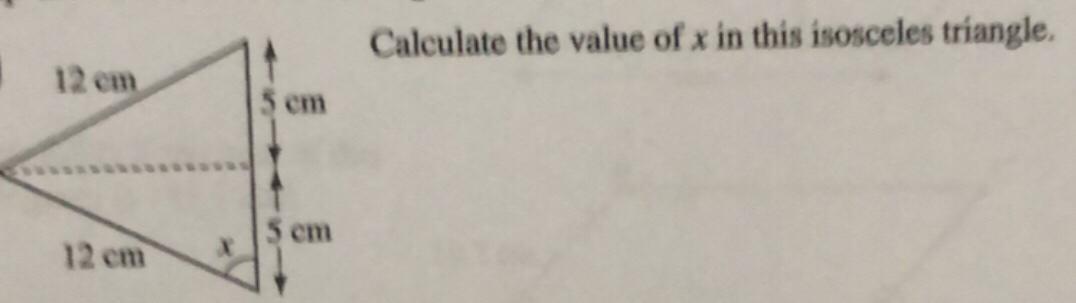
Answers
Answer:
x = 65.38°
using cosine rule:
cos(x) = \(\frac{adjacent}{hypotenuse}\)cos(x) = \(\frac{5}{12}\)x = \(cos^{-1}(\frac{5}{12} )\)x = 65.3756°x = 65.38°
The sum of a number and 3 is greater than 10
x < 7
x > 7
x < 13
x > 13
Answers
Answer:
x > 7
Step-by-step explanation:
Let x be the unknown number
x+3 > 10
Subtract 3 from each side
x+3-3 > 10-3
x > 7
\(\huge\textsf{Hey there!}\)
\(\large\textsf{\underline{The sum of a number and 3 is greater than 10.}}\)
\(\large\textsf{Well, the word sum simply means add. The word number}\\\large\textsf{ is unknown so we will label it as x.}\)
\(\large\textsf{We will make this your equation: x + 3 } \mathsf{ > } \large\textsf{ 10}\)
\(\large\textsf{Now lets solve for your answer.}\downarrow\)
\(\large\textsf{x + 3 }\mathsf{>}\large\textsf{ 10}\)
\(\large\textsf{SUBTRACT 3 to BOTH SIDES}\)
\(\large\textsf{x + 3 - 3 } \mathsf{>} \large\textsf{ 10 - 3}\)
\(\large\textsf{CANCEL out: 3 - 3 because that gives you 0}\)
\(\large\textsf{KEEP: 10 - 3 because that helps what is being compared to the x-value}\)
\(\large\textsf{x } \mathsf{>} \large\textsf{ 10 - 3}\)
\(\large\textsf{10 - 3 = \bf 7}\)
\(\large\textsf{\bf x } \mathsf{\bf >\ } \large\textsf{ \bf 7}\)
\(\boxed{\boxed{\large\textsf{Therefore, your answer is: \bf x}>\textsf{\bf 7}\huge\textsf{ (Option B.)}}}\huge\checkmark\)
\(\huge\textsf{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
1) What is measured by the denominator of the z-score test statistic?
a. the average distance between M and µ that would be expected if H0 was true
b. the actual distance between M and µ
c. the position of the sample mean relative to the critical region
d. whether or not there is a significant difference between M and µ
Answers
The correct answer is a. the average distance between M and µ that would be expected if H0 was true.
The denominator of the z-score test statistic measures the average distance between the sample mean (M) and the population mean (µ) that would be expected if the null hypothesis (H0) was true.
Option a. "the average distance between M and µ that would be expected if H0 was true" is the correct description of what is measured by the denominator of the z-score test statistic. It represents the standard error, which is a measure of the variability or dispersion of the sample mean around the population mean under the assumption of the null hypothesis being true.
Option b. "the actual distance between M and µ" is not accurate because the actual distance between M and µ is not directly measured by the denominator of the z-score test statistic.
Option c. "the position of the sample mean relative to the critical region" is not accurate because the position of the sample mean relative to the critical region is determined by the numerator of the z-score test statistic, which represents the difference between the sample mean and the hypothesized population mean.
Option d. "whether or not there is a significant difference between M and µ" is not accurate because the determination of a significant difference is based on comparing the calculated test statistic (z-score) to critical values, which involve both the numerator and the denominator of the z-score test statistic.
for such more question on z-score
https://brainly.com/question/15222372
#SPJ8
8% of all Americans live in poverty. If 36 Americans are randomly selected, find the following probabilities. Round answers to 4 decimal places. a. Probability that exactly 1 of them live in poverty. b. Probability that at most 2 of them live in poverty. c. Probability that at least 1 of them in poverty. d. Probability that between 3 and 7 (including 3 and 7 ) of them live in poverty.
Answers
P(3 to 7) = P(3) + P(4) + P(5) + P(6) + P(7).To solve the given probabilities, we can use the binomial probability formula:
P(x) = C(n, x) * p^x * (1 - p)^(n - x)
Where:
- P(x) is the probability of exactly x successes
- C(n, x) is the number of combinations of n items taken x at a time
- p is the probability of success for each trial
- n is the number of trials
Given that 8% (0.08) of all Americans live in poverty, and we are selecting 36 Americans randomly, we can calculate the following probabilities:
a) Probability that exactly 1 of them live in poverty:
P(1) = C(36, 1) * (0.08)^1 * (1 - 0.08)^(36 - 1)
b) Probability that at most 2 of them live in poverty:
P(at most 2) = P(0) + P(1) + P(2)
= C(36, 0) * (0.08)^0 * (1 - 0.08)^(36 - 0) + C(36, 1) * (0.08)^1 * (1 - 0.08)^(36 - 1) + C(36, 2) * (0.08)^2 * (1 - 0.08)^(36 - 2)
c) Probability that at least 1 of them live in poverty:
P(at least 1) = 1 - P(0)
d) Probability that between 3 and 7 (including 3 and 7) of them live in poverty:
P(3 to 7) = P(3) + P(4) + P(5) + P(6) + P(7)
Using the formula and the provided values, we can calculate these probabilities.
Learn more about probability here; brainly.com/question/31828911
#SPJ11
Unit 2: Logic & Proof
Homework 2: Compound Statements
Answers
on using disjunctive syllogism to derive Q from the second premise and the derived value of A. if P is true, then Q must also be true..
In logic, a compound statement is made up of two or more simple statements, known as premises or assumptions, that are combined using logical operators such as "and," "or," and "not." To prove a compound statement, we use rules of inference to derive a conclusion based on the given premises.
In the first proof question, we are given three premises: P, P or R, and not S or A. We need to prove the statement Q using these premises. To do so, we use the disjunctive syllogism rule, which states that if one of two disjunctive statements is false, then the other must be true. By assuming ~P, we derive ~S from the third premise using the rule of disjunction. Then, using modus ponens, we derive A from the assumption of ~P and the third premise. Finally, we use disjunctive syllogism to derive Q from the second premise and the derived value of A.
In the second proof question, we are given three premises: not P or S, not S, and R or Q. We need to prove the statement P implies Q using a conditional world proof. We assume P is true and derive S using the first premise. Using the second premise and modus tollens, we derive not R. Finally, using disjunctive syllogism, we derive Q from the third premise and the derived value of not R. Therefore, we show that if P is true, then Q must also be true..
To know more about disjunctive syllogism. click here:
brainly.com/question/22173899
#SPJ4

Find the value of a in the equation below.
5 = x - 18
Answers
Answer:
There's no A so I'm going to assume you meant X
X = 23
Step-by-step explanation:
X is equal to 23, because 23 - 18 = 5
or 5 + 18 = 23
3. In a survey of 200 people about a bus company, 77 said they were satisfied with the bus
company's performance. What percent of the people were satisfied with the bus company's
performance?
O 23%
38.5%
061.5%
077%
Answers
The percentage of the people that were satisfied with the bus company's performance is: B. 38.5%
Given the following data:
Population = 200 peopleSatisfied people = 77 peopleTo determine the percentage of the people that were satisfied with the bus company's performance:
In this exercise, you're required to find the number of the people that were satisfied with the bus company's performance as a percentage of the total population in this survey.
Thus, we would use this formula:
\(Percentage = \frac{Satisfied\;people}{Population} \times 100\)
Substituting the given parameters into the formula, we have;
\(Percentage = \frac{77}{200} \times 100\\\\Percentage = \frac{77}{2}\)
Percentage = 38.5%
Read more on percentage here: https://brainly.com/question/14432715
An independent set in a graph is a set of vertices S⊆V that contains no edge (so no pair of neighboring vertices is included). The max independent set problem is to find an independent set of maximum size in a graph G. (a) Write the max independent set problem as an integer linear program. (b) Write an LP relaxation for the max independent set problem. (c) Construct an example (a family of graphs) to show that the ratio LP-OPT / OPT can be at least cn where c>0 is some absolute constant and n is the number of vertices of the graph. (d) What is the (exact) relation between the size of a max independent set and the size of min vertex cover of a graph? (e) Using this relation, what does the 2-approximation algorithm for vertex cover imply for an approximation algorithm for max independent set?
Answers
The independent set in a graph is a set of vertices that contain no edges. So, no neighboring vertices are included. The max independent set problem is to get an independent set of maximum size in graph G.
The solution for this question is discussed below:
a) The integer linear program for the max independent set problem is as follows:
maximize ∑x_i Subject to: x_i+x_j ≤ 1 {i,j} ∈ E;x_i ∈ {0, 1} ∀i. The variable x_i can represent whether the ith vertex is in the independent set. It can take on two values, either 0 or 1.
b) The LP relaxation for the max independent set problem is as follows:
Maximize ∑x_iSubject to:
xi+xj ≤ 1 ∀ {i, j} ∈ E;xi ≥ 0 ∀i. The variable xi can take on fractional values in the LP relaxation.
c) The family of graphs is as follows:
Consider a family of graphs G = (V, E) defined as follows. The vertex set V has n = 2^k vertices, where k is a positive integer. The set of edges E is defined as {uv:u, v ∈ {0, 1}^k and u≠v and u, v differ in precisely one coordinate}. It can be shown that the size of the max independent set is n/2. Using LP, the value can be determined. LP provides a value of approximately n/4. Therefore, the ratio LP-OPT/OPT is at least c/4. Therefore, the ratio is in for a constant c>0.
d) The size of a max-independent set is equivalent to the number of vertices minus the minimum vertex cover size.
e) The 2-approximation algorithm for vertex cover implies a 2-approximation algorithm for the max independent set.
To know more about the independent set, visit:
brainly.com/question/31418821
#SPJ11
How much interest would you have to pay for a 30-month loan of
$1,735.53 if the simple interest rate were 7.11%?
Answers
Answer:
$308.49
Step-by-step explanation:
intermediate value function
Use the Intermediate Value Function to show that there is a solution to the equation in the specified interval (1,2). 4x3 - 6x2 + 3x - 2 = 0 For the toolbar, press ALT+F10 (PC) or ALT+FN+F10 (Mac)
Answers
The function must has at least one solution to the equation in the interval (1, 2).
How to use the Intermediate Value Theorem to show that there is a solution to the equation \(4x^3 - 6x^2 + 3x - 2\) = 0 in the interval (1, 2)?To use the Intermediate Value Theorem to show that there is a solution to the equation \(4x^3 - 6x^2 + 3x - 2\) = 0 in the interval (1, 2), we need to show that the function changes sign on the interval.
Let's evaluate the function at the endpoints of the interval:
\(f(1) = 4(1)^3 - 6(1)^2 + 3(1) - 2 = -1\\f(2) = 4(2)^3 - 6(2)^2 + 3(2) - 2 = 12\\\)
Since f(1) = -1 is negative and f(2) = 12 is positive, we have a sign change of the function on the interval (1, 2).
According to the Intermediate Value Theorem, if a continuous function changes sign on an interval, there must exist at least one solution to the equation within that interval.
In this case, since the function changes sign from negative to positive on the interval (1, 2), there must be at least one solution to the equation \(4x^3 - 6x^2 + 3x - 2 = 0\) in the interval (1, 2).
Learn more about Intermediate Value Theorem
brainly.com/question/29712240
#SPJ11
Kite PQRS at the right is concave. If we have PQ = QR = 20, PS= SR= 15, and QS = 7, then what is the area of kite PQRS?

Answers
The area of Kite PQRS at the right is concave. If we have PQ = QR = 20, PS= SR= 15, and QS = 7 is 220 square units
How to find the area of kite PQRSFirst, we can find the length of the diagonal PR using the Pythagorean theorem:
PR² = PQ² + QR² = 20² + 20² = 800
PR = sqrt(800) ≈ 28.28
Similarly, we can find the length of the diagonal QS:
QS² = QR² + RS² = 20² + 15² = 625
QS = sqrt(625) = 25
Now, we can split the kite into two triangles, PQS and QRS, and use the formula for the area of a triangle:
area of PQS = (1/2) * PQ * QS = (1/2) * 20 * 7 = 70
area of QRS = (1/2) * QR * RS = (1/2) * 20 * 15 = 150
So the total area of the kite is:
area of PQRS = area of PQS + area of QRS = 70 + 150 = 220
Therefore, the area of kite PQRS is 220 square units
Learn more about kite at https://brainly.com/question/26870235
#SPJ1
It takes 40 seconds to cut 10 in to 10 in cake into 2 to 2 in cake. how long will it take to cut 12 to 12 inch?
Answers
Answer:
60 seconds or 1 minute.Step-by-step explanation:
We need to cut each side of 10 in cake to:
10/2 = 5 piecesIt is possible by 4 cuts. In total the number of cuts is:
4 + 4 = 8Total length of the cuts is:
8*10 = 80 inIt took 40 seconds to cut 80 in so each inch of cut takes:
40/80 = 0.5 secondNow, total length of cuts of 12 in x 12 in cake is:
(5 + 5)*12 = 120 inTime required to cut this cake is:
120*0.5 = 60 secondsg assuming the sample was randomly selected and the data is normally distributed, conduct a formal hypothesis test to determine if the population mean length of stay is significantly different from 6 days.
Answers
If the null hypothesis is rejected, we can conclude that there is evidence to suggest that the population mean length of stay is significantly different from 6 days.
If the null hypothesis is not rejected, we do not have sufficient evidence to conclude a significant difference.
What is Hypothesis?
A hypothesis is an assumption, an idea that is proposed for the purpose of argumentation so that it can be tested to see if it could be true. In the scientific method, a hypothesis is constructed before any applicable research is done, other than a basic background review.
To conduct a formal hypothesis test to determine if the population mean length of stay is significantly different from 6 days, we can set up the null and alternative hypotheses and perform a statistical test.
Null Hypothesis (H0): The population mean length of stay is equal to 6 days.
Alternative Hypothesis (H1): The population mean length of stay is significantly different from 6 days.
We can perform a t-test to compare the sample mean with the hypothesized population mean. Let's denote the sample mean as x and the sample standard deviation as s. We will use a significance level (α) of 0.05 for this test.
Collect a random sample of length of stay data. Let's assume the sample mean is x and the sample standard deviation is s.
Calculate the test statistic t-value using the formula:
t = (x - μ) / (s / √n)
Where μ is the hypothesized population mean (6 days), n is the sample size, x is the sample mean, and s is the sample standard deviation.
Determine the degrees of freedom (df) for the t-distribution. For a one-sample t-test, df = n - 1.
Find the critical t-value(s) based on the significance level and degrees of freedom. This can be done using a t-distribution table or a statistical software.
Compare the calculated t-value with the critical t-value(s). If the calculated t-value falls within the rejection region (i.e., outside the critical t-values), we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis.
Calculate the p-value associated with the calculated t-value. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed data, assuming the null hypothesis is true. If the p-value is less than the chosen significance level (α), we reject the null hypothesis.
Make a conclusion based on the results. If the null hypothesis is rejected, we can conclude that there is evidence to suggest that the population mean length of stay is significantly different from 6 days. If the null hypothesis is not rejected, we do not have sufficient evidence to conclude a significant difference.
To learn more about Hypothesis from the given link
https://brainly.com/question/606806
#SPJ4
Convert the temperature from degrees Celsius to degrees Fahrenheit, using the formula below.

Answers
Answer:
correct answer 176
Step-by-step explanation:
Answer:
\(80 \: c = 176 \: f\)
Step-by-step explanation:
\(f = ( \frac{9}{5} \times c) + 32 \\ f = ( \frac{9}{5} \times 80) + 32 \\ f = (\frac{720}{5} ) + 32 \\ f = 144 + 32 = 176\)
interpret this bound. with 95% confidence, we can say that the value of the true mean proportional limit stress of all such joints is centered around this value. with 95% confidence, we can say that the value of the true mean proportional limit stress of all such joints is greater than this value. with 95% confidence, we can say that the value of the true mean proportional limit stress of all such joints is less than this value. what, if any, assumptions did you make about the distribution of proportional limit stress? we must assume that the sample observations were taken from a normally distributed population. we do not need to make any assumptions. we must assume that the sample observations were taken from a chi-square distributed population. we must assume that the sample observations were taken from a uniformly distributed population.
Answers
The answer is that with 95% confidence, we can say that the value of the true mean proportional limit stress of all such joints is centered around a certain value. This means that we are fairly certain that the true value lies within a certain range.
This bound is based on statistical analysis and assumes that the sample observations were taken from a normally distributed population. This means that the data follows a bell curve shape, with most of the values falling near the mean and fewer values falling farther away from the mean. The 95% confidence level means that if we were to repeat the experiment multiple times, we would expect the true value to lie within this range 95% of the time.
We cannot say for certain whether the true mean proportional limit stress is greater or less than the value we have calculated, but we can say that it is centered around this value with a high degree of confidence.
It is important to note that this bound is based on certain assumptions about the data and the population it represents. If these assumptions are not met, the bound may not be accurate or valid.
To know more about statistical analysis visit:
brainly.com/question/30154483
#SPJ11
5/6x + 7 = 17 (step by step pls)
Answers
5/6x + 7 = 17
Subtract 7 from both sides:
5/6x = 10
Divide both sides by 5/6:
X = 10/ 5/6
When dividing a number by a fraction flip
The fraction over and multiply:
X = 10 x 6/5
Simplify
X = (10x6)/5
X = 60/5
X = 12
The answer is x = 12
Answer:
\(\boxed {x = 12}\)
Step-by-step explanation:
Solve for the value of \(x\):
\(\frac{5}{6}x + 7 = 17\)
-Subtract both sides by \(7\):
\(\frac{5}{6}x + 7 - 7 = 17 - 7\)
\(\frac{5}{6}x = 10\)
-Multiply both sides by \(\frac{6}{5}\), which is the reciprocal of \(\frac{5}{6}\):
\(x = 10 \times (\frac{6}{5})\)
\(x = \frac{10 \times 6}{5}\)
\(x = \frac{60}{5}\)
-Divide \(60\) by \(5\):
\(x = \frac{60}{5}\)
\(\boxed {x = 12}\)
Therefore, the value of \(x\) is \(12\).
Calculate the future value of $76,010.00, earning interest at a rate of 2 1/5% of that is compounded daily for 2 years.$76,010.00$79,429.00$6,109,851.09$778,342.40
Answers
Given;
\(\begin{gathered} Principal(P)=76010.00 \\ rate(r)=2\frac{1}{5}\%=\frac{11}{5}\%=2.2\%=0.022 \end{gathered}\)To Determine: The future value after 2 years if the compounded daily
Solution:
The future value of a compound interest is calculated using the formula
\(A=P(1+\frac{r}{n})^{nt}\)\(\begin{gathered} Where \\ A=Future\text{ value} \\ P=Principal(amount\text{ invested\rparen} \\ r=rate \\ n=365\text{ for daily compounds\rparen} \\ t=time\text{ in years} \end{gathered}\)Substitute the given into the formula
\(\begin{gathered} A=76010(1+\frac{0.022}{365})^{365\times2} \\ A=76010(1+0.00006027397)^{730} \end{gathered}\)\(\begin{gathered} A=76010(1.00006027397)^{730} \\ A=79429.00 \end{gathered}\)Hence, the future value is $79,429.00