the Angle opposite The OPP is
Answers
Answer:
Theta
Step-by-step explanation:
Indeed all angles of a triangle have a opposite side. And in trigonometry, the side opposite to theta is opposite side
Related Questions
Can get a little help

Answers
Good luckvsvsvsbsbsjsjhsbsbsbsb
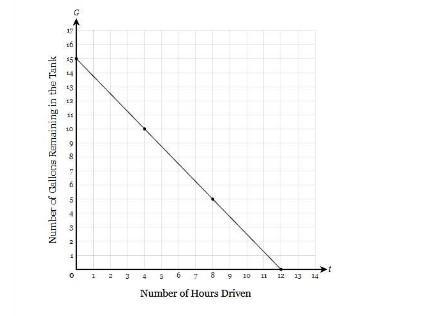
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
A circle is centered at the origin and has radius of 10. A particle starts at point (10,0) and travels counterclockwise on the circle, making one complete revolution every 9 seconds. Write the parametric equations for the motion of the particle, where t represents time in seconds:
x(t) = ?
y(t) = ?
Answers
The parametric equations for the motion of the particle are:
x(t) = 10 cos(2πt/9)
y(t) = 10 sin(2πt/9)
Here, t represents time in seconds, and 2π/9 represents the angular speed of the particle, since it completes one revolution every 9 seconds. The radius of the circle is 10, which is used in the equations for the x and y coordinates of the particle's position at any given time t.
For more questions like radius visit the link below:
https://brainly.com/question/29836862
#SPJ11
HELP PLZ can someone simplify this equation

Answers
7n² + 48n + 42
Combine like terms, -8n x -6n= 48n
-6 x -7= 42
Answer:
-49n^3 -n²+92n+42
Step-by-step explanation:
(7n²-8n-6)(-6n-7)
-42n^3-49n²+48n²+56n+36n+42
-49n^3 -n²+92n+42
Solve please:
1/4x + 1/2 - 8 = 3x - 3/4
Answers
Answer:
x=-27/11
Step-by-step explanation:
This answer is x=-27/11
How do i solve this?

Answers
Answer:
O
Step-by-step explanation:
What is a Graphic representation of association between variables
Answers
An equation is shown 3/5k=225. what is the value for k that makes the equation true?
Answers
Answer:
.0024
Step-by-step explanation:
3 = 225 x 5k
3/255 = 5k
5k = 0.117
k=0.0024
evaluate the expression 6x + 4 9/10 when x = 2/3.
Answers
x=2/3
6(2/3) + 4 9/10 =4 + 4 9/10 = 8 9/10
Answer:
2x-1=y,2y+3=x
Step-by-step explanation:
no explanation
It's believed that as many as 21% of adults over 50 never graduated from high school. We wish to see if this percentage is the same among the 25 to 30 age group. a) How many of this younger age group must we survey in order to estimate the proportion of non-grads to within 10% with 90% confidence? n= (Round up to the nearest integer.)
Answers
A minimum sample size of 121 individuals needs to be surveyed, ensuring a rounded-up value to estimate the proportion of non-graduates within the 25 to 30 age group with a 10% margin of error and 90% confidence.
To determine the sample size required to estimate the proportion of non-graduates within the 25 to 30 age group with a certain level of confidence and margin of error, we can use the formula:
n = (Z^2 * p * (1 - p)) / E^2
Where:
n is the required sample size
Z is the Z-score corresponding to the desired confidence level (90% confidence corresponds to a Z-score of approximately 1.645)
p is the estimated proportion of non-graduates (0.21 based on the information provided)
E is the desired margin of error (10% or 0.10)
Substituting the values into the formula:
n = (1.645^2 * 0.21 * (1 - 0.21)) / 0.10^2
n ≈ 120.41
Rounding up to the nearest integer, the required sample size is 121.
Therefore, you would need to survey at least 121 individuals in the 25 to 30 age group to estimate the proportion of non-graduates within 10% margin of error with 90% confidence.
To know more about sample size refer here:
https://brainly.com/question/30100088#
#SPJ11
Which equation represents a line that is parallel to
the line y = - 4x +5?
(A) y=-4x +3
(B) y=-x+3
(C) y=-=x+5
(D) y = 4x + 5
Answers
Answer:
A. y = -4x + 3
Step-by-step explanation:
Parallel lines have the same slope, but will have a different y-intercept.
In the equation y = -4x + 5, -4 is the slope.
This means a line that is parallel to this one will also have a slope of -4.
So, this means that A is the correct answer, because it has a slope of -4.
y = -4x + 3 denotes a line that is parallel to y = - 4x +5. Parallel lines are two lines in the same plane that are equal in length and never intersect.
How can a line that is parallel to a line be found?By comparing the slopes of two lines, we can determine whether they are parallel. When two lines have the same slope but different y-intercepts, they are said to be parallel.The lines are not parallel if the slopes differ. axes that are parallel We can use their equations to compare the slopes of two lines to see if they are parallel. If the slopes are the same but the y-intercepts are different, the lines are parallel. If the slopes differ, the lines are not parallel. m is the slope in the generic linear equation y = mx + b.Therefore,
Points of axis interception y = -4x + 5
-4x + 5 : m = -4
Same as,
y = -4x + 3
Simplifying the above equation, then we get
-4x + 3 : m = -4
Hence, y = -4x + 3 denotes a line that is parallel to y = - 4x +5.
To learn more about linear equation refer to:
brainly.com/question/17828867
#SPJ2
What is the median of 5,2,9,21,12,3
Answers
Answer: 7
Step-by-step explanation:
First order the numbers by least to greatest
2, 3, 5, 9, 12, 21
Then find the number inbetween
In this case it's a tie between 5 and 9.
Find the average of those two numbers
The average is 5+9/2 = 7
Median is 7
Hello solve this, what is 9 x 5/7
Answers
Answer: 6 3/7
Step-by-step explanation:
9/1 x 5/7
If we multiply the numerators and denominators, we get 45/7 or 6 3/7 as a mixed number.
Answer:
\(\frac{45}{7}\) or 6.4285
Step-by-step explanation:
First, multiply 9 and 5, which gives you 45.
9(5)=45
Then, divide 45 by 7.
45/7=6.4285
That gives you \(\frac{45}{7}\) or 6.4285
Hope this helps!
Jessica's business has 83 rolls of toilet paper. Customers use 3 rolls of toilet paper per day.
Write an expression to represent the amount of toilet paper after d days. i dont understand can someone post an answer an explain?
Answers
a package of 6 pairs of insulated socks cost $85.20 what is the unit price of thepairs of socks
Answers
pls help me guys i have no idea what im doing...

Answers
90 + x + 3x = 180
4x = 90
x = 22.5
Your answer: 22.5
what is the arc length of a semicircle with a diameter of 8
Answers
Answer:
\( \frac{88}{7} units\)
Step-by-step explanation:
Circumference of semi-circle=
\(\pi \: r\)
\( \frac{22}{7} \times 4 \\ \frac{88}{7} \)
points
What is the distance between (-9, -6) and (-2,-2)?
Answers
Step-by-step explanation:
-7 and -4? I guess here u go
Answer:
9
Step-by-step explanation:
There is a simple formula that can be applied here, appropriately termed the distance formula. It is d = sqrt( (x2 - x1)^2 + (y2 - y1)^2 ), where (x1,y1) and (x2,y2) are the two given points. It doesn't matter which point is which, it ends up being the same since both binomials are being squared. The formula is simply an application of the Pythagorean theorem. In coordinate space, you're constructing a right triangle using the line connecting the two points as the hypotenuse, with horizontal and vertical lines as the legs. Then it's simply c^2 = a^2 + b^2, and you can get the distance formula by square rooting both sides.
5 5 5 are my numbers to find surface area of a pyramid using nets how do I do that?
Answers
To find the surface area of a pyramid using nets with base side length of 5 units and height of 5 units, calculate the area of the base and the area of the triangular faces, then sum them up. Therefore, the surface area of the pyramid, using the given net, is approximately 68.32 square units.
To determine the surface area of a pyramid, we can use the concept of nets. A net is a two-dimensional representation of a three-dimensional shape that can be unfolded to reveal its faces. In the case of a pyramid, the net consists of a base shape and triangular faces that connect to the apex.
Given that the base side length is 5 units and the height is also 5 units, we first calculate the area of the base. Since the base is a square, the area is given by multiplying the length of one side by itself: 5 * 5 = 25 square units.
Next, we calculate the area of each triangular face. The formula for the area of a triangle is 1/2 * base * height. The base of each triangular face is the side length of the base, which is 5 units. The height can be found using the Pythagorean theorem, where one leg is half the base length and the other leg is the height of the pyramid. So the height is √(5^2 - \((5/2)^2) = √(25 - 6.25) = √18.75\) ≈ 4.33 units. Thus, the area of each triangular face is 1/2 * 5 * 4.33 = 10.83 square units.
Finally, we sum up the area of the base and the area of the triangular faces: 25 + (4 * 10.83) = 68.32 square units. Therefore, the surface area of the pyramid, using the given net, is approximately 68.32 square units.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
To find the surface area of a pyramid using nets with base side length of 5 units and height of 5 units, you can calculate the area of the base and the area of the triangular faces. Then, sum up these areas to determine the total surface area of the pyramid.
Layla invested $380 in an account paying an interest rate of 5 7/8% compounded quarterly. Brandon invested $380 in an account paying an interest rate of 6 1/8% compounded monthly. To the nearest hundredth of a year, how much longer would it take for Layla's money to triple than for Brandon's money to triple
Answers
so hmmm tripling $380 we end up with $1140, now, since 7/8 is 0.875, that means that Layla's rate is 5.875, whilst Brandon's is 6.125.
\(~~~~~~ \stackrel{ \textit{\LARGE Layla}}{\textit{Compound Interest Earned Amount}} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 1140\\ P=\textit{original amount deposited}\dotfill &\$380\\ r=rate\to 5.875\%\to \frac{5.875}{100}\dotfill &0.05875\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{quarterly, thus four} \end{array}\dotfill &4\\ t=years \end{cases}\)
\(1140 = 380\left(1+\frac{0.05875}{4}\right)^{4\cdot t} \implies \cfrac{1140}{380}=1.0146875^{4t} \\\\\\ 3=1.0146875^{4t}\implies \log(3)=\log(1.0146875^{4t}) \\\\\\ \log(3)=t\log(1.0146875^{4})\implies \cfrac{\log(3)}{\log(1.0146875^{4})}=t\implies \boxed{18.84\approx t} \\\\[-0.35em] ~\dotfill\)
\(~~~~~~ \stackrel{ \textit{\LARGE Brandon}}{\textit{Compound Interest Earned Amount}} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 1140\\ P=\textit{original amount deposited}\dotfill &\$380\\ r=rate\to 6.125\%\to \frac{6.125}{100}\dotfill &0.06125\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus twelve} \end{array}\dotfill &12\\ t=years \end{cases}\)
\(1140 = 380\left(1+\frac{0.06125}{12}\right)^{12\cdot t} \implies \cfrac{1140}{380}=\left( \cfrac{9649}{9600} \right)^{12t}\implies 3=\left( \cfrac{9649}{9600} \right)^{12t} \\\\\\ \log(3)=\log\left[ \left( \cfrac{9649}{9600} \right)^{12t} \right]\implies \log(3)=t\log\left[ \left( \cfrac{9649}{9600} \right)^{12} \right]\)
\(\cfrac{\log(3)}{ ~~ \log\left[ \left( \frac{9649}{9600} \right)^{12} \right] ~~ }=t\implies \boxed{17.98\approx t} \\\\[-0.35em] ~\dotfill\\\\ 18.84~~ - ~~17.98 ~~ \approx ~~ \text{\LARGE 0.86}\)
CAN SOMEONE HELP ME PLS I GIBE BRAINLIST AND POINTS

Answers
Answer:
184.26
Step-by-step explanation:
28.275 + 60 + 96 = 184.26
An aircraft carrier can travel 450 km in the same time a container ship travels 300 km. If the aircraft carrier was travelling 5 km/h faster what was the speed of the container ship?
Answers
Answer:
10 Km/h
Step-by-step explanation:
Let the speed of the container ship be y
The speed of the aircraft = y + 5
Next, we shall determine the time taken by the aircraft to travel 450 Km. This can be obtained as follow:
Speed of aircraft (Sₐ) = y + 5
Distance travelled (dₐ) = 450 Km
Time for aircraft (tₐ) =?
Speed = distance / time
Sₐ = dₐ / tₐ
y + 5 = 450 / tₐ
Cross multiply
(y + 5) × tₐ = 450
Divide both side by (y + 5)
tₐ = 450 / (y + 5)
Finally, we shall determine the speed of the carrier. This can be obtained as follow:
Speed of container ship (S꜀) = y
Distance travelled (d꜀) = 300 Km
Time for container ship (t꜀) = Time for aircraft (tₐ)
Time for aircraft (tₐ) = 450 / (y + 5)
t꜀ = tₐ
t꜀ = 450 / (y + 5)
Speed = distance / time
S꜀ = d꜀ / t꜀
y = 300 ÷ 450 / (y + 5)
y = 300 × (y + 5) / 450
y = (300y + 1500) / 450
Cross multiply
450y = 300y + 1500
Collect like terms
450y – 300y = 1500
150y = 1500
Divide both side by 150
y = 1500 / 150
y = 10 Km/h
Thus, the speed of the container ship is 10 Km/h.
The local bank has a single line for customers waiting for the next available bank teller. There are four bank tellers who work at the same rate. The arrival rate of customers follows a Poisson distribution, while the service time follows an exponential distribution. Customers arrive at the bank at a rate of about twelve every hour. On average, it takes about 15 minutes to serve each customer. Answers to 2 d.p's.
(a) Calculate the probability that the bank is empty.
(b) Calculate the average time the customer spends waiting to be called.
(c) Calculate the average number of customers in in the bank.
(d) The average number of customers waiting to be served
Answers
a) The probability that the bank is empty is approximately 0.0026.
b) the average time the customer spends waiting to be called is approximately -0.25 c) hours the average number of customers in the bank is -1.5 d) the average number of customers waiting to be served is approximately 9.
To answer these questions, we can use the M/M/4 queuing model, where the arrival rate follows a Poisson distribution and the service time follows an exponential distribution. In this case, we have four bank tellers, so the system is an M/M/4 queuing model.
Given information:
Arrival rate (λ) = 12 customers per hour
Service rate (μ) = 1 customer every 15 minutes (or 4 customers per hour)
(a) To calculate the probability that the bank is empty, we need to find the probability of having zero customers in the system. In an M/M/4 queuing model, the probability of having zero customers is given by:
P = (1 - ρ) / (1 + 4ρ + 10ρ² + 20ρ³)
where ρ is the traffic intensity, calculated as ρ = λ / (4 * μ).
ρ = (12 customers/hour) / (4 customers/hour/teller) = 3
Substituting ρ = 3 into the formula, we have:
P = (1 - 3) / (1 + 4 * 3 + 10 * 3² + 20 * 3³) ≈ 0.0026
Therefore, the probability that the bank is empty is approximately 0.0026.
(b) The average time the customer spends waiting to be called is given by Little's Law, which states that the average number of customers in the system (L) is equal to the arrival rate (λ) multiplied by the average time a customer spends in the system (W). In this case, we want to find W.
L = λ * W
W = L / λ
Since the average number of customers in the system (L) is given by L = ρ / (1 - ρ), we can substitute this into the equation to find W:
W = L / λ = (ρ / (1 - ρ)) / λ
W = (3 / (1 - 3)) / 12 ≈ -0.25
Therefore, the average time the customer spends waiting to be called is approximately -0.25 hours, which is not a meaningful result. It seems there might be an error in the given data.
(c) The average number of customers in the bank (L) can be calculated as:
L = ρ / (1 - ρ) = 3 / (1 - 3) = -1.5
Therefore, the average number of customers in the bank is -1.5, which is not a meaningful result. It further suggests an error in the given data.
(d) The average number of customers waiting to be served can be calculated as:
\(L_q\) = (ρ² / (1 - ρ)) * (4 - ρ)
Substituting ρ = 3, we have:
\(L_q\\\) = (3² / (1 - 3)) * (4 - 3) ≈ 9
Therefore, the average number of customers waiting to be served is approximately 9.
For more about probability:
brainly.com/question/31828911
#SPJ4
A skier is trying to decide whether or not to buy a season ski pass. A daily pass costs $77. A season ski pass costs $450. The skier would have to rent skis with either pass for $20 per day. How many days would the skier have to go skiing in order to make the season pass less expensive than the daily passes?

Answers
Answer:
5
Step-by-step explanation:
Given:
Daily pass = $77Season ski pass = $450Skis = 2077 + 20 = 97
450 + 20 = 470
Keep multiplying 97 with random numbers until it passes 470.
97 × 4 = 388
97 × 5 = 485
So, the skier will have to pay daily passes 5 times to be more expensive than the season pass.
Hope this helped.
Add these fractions, giving your answer
in its simplest form.
6/12 + 2/13 =?
Answers
Answer: 0.6 espero haberte ayuado
Step-by-step explanation:
Select TWO expressions that have the same value as -4 - (-12).
-4 + 12
12-4
-4 - 12
4 + 12
12 - (-4)

Answers
Answer:
-4+12
12-4
Step-by-step explanation:
Expression 1:
-4 - (-12)=
-4+12=
8
Expression 2:
12-4=
8
Answer:
12-(-4)
Step-by-step explanation:
Using the master theorem read off the Θ order of the following recurrences: (a) T(n)=2T(n/2)+n
2
(b) T(n)=2T(n/2)+n (c) T(n)=4T(n/2)+n (d) T(n)=T(n/4)+1
Answers
1. T(n) = Θ(n)
2. T(n) = Θ(n)
3. T(n) = Θ(n²)
4. T(n) = Θ(1)
The master theorem is an algorithmic approach for solving recurrence relations (both divide and conquer and recursive equations). Let us use the master theorem to read off the Θ order of the following recurrences:
(a) T(n) = 2T(n/2) + n²:
Using the Master theorem: a = 2, b = 2 and f(n) = n² so
logba = log2/ log2 = 1 = c(n²) = Θ(nlogba) = Θ(n)
Therefore T(n) = Θ(nlogba) = Θ(nlog₂2) = Θ(n)
(b) T(n) = 2T(n/2) + n:
Using the Master theorem: a = 2, b = 2 and f(n) = n so
logba = log2/ log2 = 1 = c(n) = Θ(nlogba) = Θ(n)
Therefore T(n) = Θ(nlogba) = Θ(nlog₂2) = Θ(n)
(c) T(n) = 4T(n/2) + n:
Using the Master theorem: a = 4, b = 2 and f(n) = n so
logba = log4/ log2 = 2 = c(n²) = Θ(n²)
Therefore T(n) = Θ(nclogba) = Θ(n²log₂4) = Θ(n²)
(d) T(n) = T(n/4) + 1:
Using the Master theorem: a = 1, b = 4 and f(n) = 1 so logba = log4/ log1 = undefined
Therefore T(n) = Θ(nclogba) = Θ(n⁰) = Θ(1)
Learn more about recurrence:
https://brainly.com/question/31789425
#SPJ11
Is b a scaled copy of R ? If so, what is the scale factor?

Answers
Answer:
Yes
Step-by-step explanation:
I'm guessing so tell me if I'm wrong :(
In ΔRST, m ∠ R = ( 5 x + 15 ) ∘ m∠R=(5x+15) ∘ , m ∠ S = ( 6 x + 8 ) ∘ m∠S=(6x+8) ∘ , and m ∠ T = ( 4 x + 7 ) ∘ m∠T=(4x+7) ∘ . What is the value of x ? x?
Answers
Answer:
X=2
Step-by-step explanation:
5x+15+6x+8+4x+7=60
combine like term
5x+6x+4x=15x
15+8+7=30
subtract 30 from both sides
15x+30=60
-30. -30
15x=30
divide 15 from 30
X=2
What is the rule of SAS criteria?
Answers
We have defined the criteria for SAS congruency of triangles.
What is SAS?
The SAS theorem states that "Triangles are congruent if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle."
According to the SAS criteria for triangle similarity, two sides of one triangle are similar to two sides of another triangle if their included angles are congruent.
Hence, we have defined the criteria for SAS congruency of triangles.
To learn more about the SAS congruency of triangles, visit:
brainly.com/question/13408604
#SPJ4