The army reports that the distribution of waist sizes among female soldiers is approximately normal, with a mean of 28.4 inches and a standard deviation of 1.2 inches.
Part A: A female soldier whose waist is 26.1 inches is at what percentile? Mathematically explain your reasoning and justify your work.
Part B: The army uniform supplier regularly stocks uniform pants between sizes 24 and 32. Anyone with a waist circumference outside that interval requires a customized order. Describe what this interval looks like if displayed visually. What percent of female soldiers requires custom uniform pants? Show your work and mathematically justify your reasoning.
Answers
Using the normal distribution, it is found that:
a) Her waist is at the 2.74th percentile.
b) 99.86% of female soldiers requires custom uniform pants.
Normal Probability DistributionThe z-score of a measure X of a normally distributed variable with mean \(\mu\) and standard deviation \(\sigma\) is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score measures how many standard deviations the measure is above or below the mean. Looking at the z-score table, the p-value associated with this z-score is found, which is the percentile of X.The mean and the standard deviation are given, respectively, by:
\(\mu = 28.4, \sigma = 1.2\).
Item a:
The percentile is the p-value of Z when X = 26.1, hence:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{26.1 - 28.4}{1.2}\)
Z = -1.92
Z = -1.92 has a p-value 0.0274 = 2.74th percentile.
Item b:
The proportion is the p-value of Z when X = 32 subtracted by the p-value of Z when X = 24, hence:
X = 32:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{32 - 28.4}{1.2}\)
Z = 3.
Z = 3 has a p-value 0.9987.
X = 24:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{24 - 28.4}{1.2}\)
Z = -3.67.
Z = -3.67 has a p-value 0.0001.
0.9987 - 0.0001 = 0.9986 = 99.86% of female soldiers requires custom uniform pants.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
Related Questions
There are 35 boys in 6th grade. The number of girls in 6th grade is 40. Emma says that means the ratio of the number of boys in 6th grade to the number of girls in 6th grade is 3:4. Is Emma correct? If not, what is the correct answer? it is the answer
correct ratio
7:8
5:8
8:7
Answers
Answer:
The correct ratio is 7:8, so no, Emma is not correct.
Hello cayleahm253!
\( \huge \boxed{\mathbb{QUESTION} \downarrow}\)
There are 35 boys in 6th grade. The number of girls in 6th grade is 40. Emma says that means the ratio of the number of boys in 6th grade to the number of girls in 6th grade is 3:4. Is Emma correct? If not, what is the correct answer?
\( \large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}\)
Okay, so we can see from the question that there are 35 boys & 40 girls in the 6th grade. So the ratio of boys is to girls will be 35:40.
__________________
Solving...
\(35 : 40 \\ = \frac{35}{40} \\ \\ \sf \: Cancel \: out \: 35 \: and \: 40 \: to \: get \: 7 \: and \: 8.\\ \\ = \frac{7}{8} \\ = \huge \boxed{\boxed{\bf \: 7 : 8}}\)
__________________
So, the correct ratio is not 3:4. Instead it's 7:8.__________________
Hope it'll help you ッ
ℓucαzz
MARKING BRAINLEIST IF YOUR ANSWER IS CORRECT!

Answers
Answer:
1 /5
Step-by-step explanation:
Write equivalent fractions for
2/3
and
5/12
using the least common denominator.
Answers
The equivalent fractions for 2/3 is (3×2)/(3×3) = 6/9 and for 5/12 is (4×5)/(4×12) = 20/48.
What is a fraction?A fraction is written in the form of p/q, where q ≠ 0.
Fractions are of two types they are proper fractions in which the numerator is smaller than the denominator and improper fractions where the numerator is greater than the denominator.
The equivalent fraction for 2/3 is (3×2)/(3×3) = 6/9.
The equivalent fraction for 5/12 is (4×5)/(4×12) = 20/48.
We have to multiply the same number to both the numerator and denominator to get equivalent fractions.
learn more about fractions here :
https://brainly.com/question/10354322
#SPJ1
Determine the domain of the following graph:
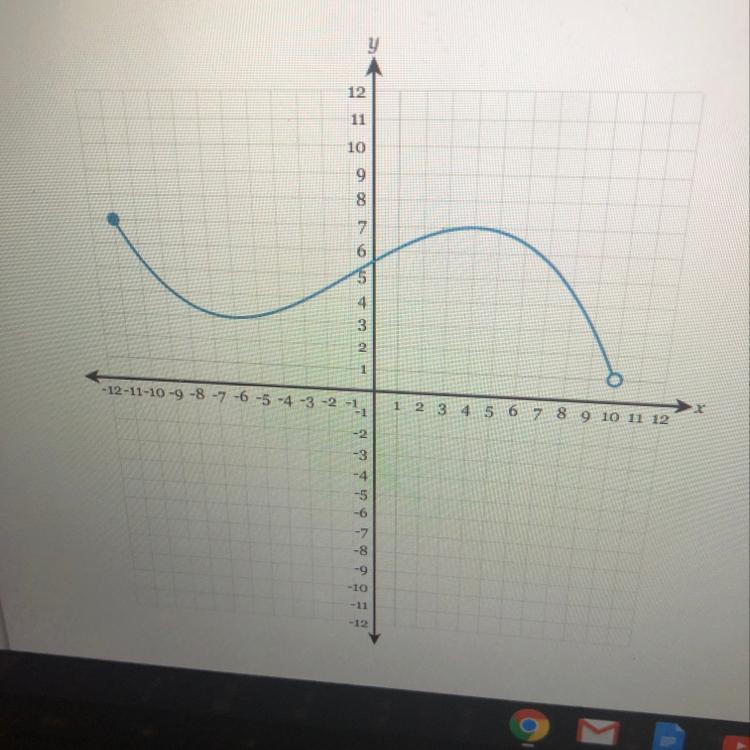
Answers
Answer and explanation:
The domain would be [-11,10). -11 has a bracket because there is a closed circle for -11; while 10 only has a parenthesis because there is an open circle. You can use every number between -11 and 10, including -11 (because of the closed circle).
Answer:
x is greater than or equal to -11 and less than 10.
Step-by-step explanation:
On the left it is a solid filled in dot which includes the -11 and on the right the dot is open so 10 is not included.
what is the probability that a photon with the polatization state you just calculated will be transmitted through a subsequent filter, that is aligned with the h direction.
Answers
The maximum probability that a photon with the polarization state will be transmitted through the A filter is 1/2
To solve this problem, we need to use Malus' law, which states that the intensity of light transmitted through a polarizer is proportional to the square of the cosine of the angle between the polarization direction of the incoming light and the axis of the polarizer.
To find the overall probability that a photon will be transmitted through all three filters, we need to multiply the probabilities of each filter
P = 1/2 × cos²(θ) × 1
We are not given the angle θ, so we cannot calculate the exact value of P. However, we can calculate the maximum value of P, which occurs when the rotated filter is aligned with the A filter (i.e., θ = 0). In this case, P = 1/2.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
The given question is incomplete, the complete question is:
H filter Rotated filter Rotated filter followed by A filter An unpolarized photon beam is incident on a linear polarizing filter. The incoming photon flux is is 2.34 x 101 photons/m' /sec. What is the probability that a photo with the polarization state be transmitted through a subsequent filter, that is aligned with the direction?
Jelena has a piece of fabric in the shape of a parallelogram the height is 10 feet and its base is 16 feet because the fabric into four equal parallelograms by current base and the height in half what is the
Answers
Complete question :
Jelena has a piece of fabric in the shape of a parallelogram the height is 10 feet and its base is 16 feet because the fabric into four equal parallelograms by current base and the height in half what is the area of each new parallelogram?
Answer:
40 ft²
Step-by-step explanation:
Given that:
Height = 10 feets
Base = 16 feets
Area of parallelogram = height * base
Area of parallelogram = 10 * 16 = 160 ft²
Area of each new parallelogram :
Area of parallelogram / number of divisions
= 160ft² / 4
= 40 ft²
Which i the correct implified verion of the expreion 32x 8 – 34x? A. 66x 8B. 74x C. -2x 8D. 6x
Answers
The simplified version of the equation 32x + 8 - 34x is -2x +8
Given that,
The equation is 32x + 8 - 34x
To find : The simplified version of 32x + 8 - 34x ?
Since the terms involving x are "like" terms, when the terms are joined, their coefficients are added.
= 32x -34x +8
= (32 -34)x +8 . . . . . x is factored out according to the distributive property
= -2x +8
Therefore, the simplified version of 32x + 8 - 34x is given as -2x +8
To learn more about equation click here:
brainly.com/question/29657988
#SPJ4
A bueket that weighs 4lb and a rope of negligible weight are used to draw water from a well that is the bucket at a rate of 0.2lb/s. Find the work done in pulling the bucket to the top of the well
Answers
Therefore, the work done in pulling the bucket to the top of the well is 4h lb.
To find the work done in pulling the bucket to the top of the well, we need to consider the weight of the bucket and the work done against gravity. The work done against gravity can be calculated by multiplying the weight of the bucket by the height it is lifted.
Given:
Weight of the bucket = 4 lb
Rate of pulling the bucket = 0.2 lb/s
Let's assume the height of the well is h.
Since the bucket is lifted at a rate of 0.2 lb/s, the time taken to pull the bucket to the top is given by:
t = Weight of the bucket / Rate of pulling the bucket
t = 4 lb / 0.2 lb/s
t = 20 seconds
The work done against gravity is given by:
Work = Weight * Height
The weight of the bucket remains constant at 4 lb, and the height it is lifted is the height of the well, h. Therefore, the work done against gravity is:
Work = 4 lb * h
Since the weight of the bucket is constant, the work done against gravity is independent of time.
To know more about work done,
https://brainly.com/question/15423131
#SPJ11
Research has shown that IQ scores have been increasing for years (Flynn, 1984, 1999). The phenomenon is called the Flynn effect and the data indicate that the increase appears to average about 7 points per decade. To examine this effect, a researcher obtains an IQ test with instructions for scoring from 10 years ago and plans to administers the test to a sample of n = 25 of today’s high school students. Ten years ago, the scores on this IQ test produced a standardized distribution with a mean of μ = 100 and a standard deviation σ = 15. If there actually has been a 7-point increase in the average IQ during the past 10 years, then find the power of the hypothesis test for each of the following.
a. The researcher uses a two-tailed hypothesis test with α = .05 to determine if the data indicate a significant change in IQ over the past 10 years.
b. The researcher uses a one-tailed hypothesis test with α = .05 to determine if the data indicate a significant increase in IQ over the past 10 years.
Answers
A. The power of the two-tailed hypothesis test with α = .05 is 0.53.
B. The power of the one-tailed hypothesis test with α = .05 is 0.95.
What is hypothesis test?A hypothesis test is used to make decisions about a population based on sample data. It involves specifying a null hypothesis, collecting data, and then assessing the data to either reject or accept the null hypothesis.
A. The power of the two-tailed hypothesis test is calculated using the formula:
Power=
1- β=1- (1-α)\(^{1/2}\)
=1- (1-0.05)\(^{1/2}\)
=0.525
=0.53
This means that the researcher has an 53% chance of correctly rejecting the null hypothesis that there has been no change in the IQ over the past 10 years.
B. The power of the one-tailed hypothesis test is calculated using the formula:
Power=
1- β=1- α
=1- 0.05
= 0.95
This means that the researcher has a 95% chance of correctly rejecting the null hypothesis that there has been no increase in the IQ over the past 10 years.
This is a higher power than the two-tailed test because the one-tailed test focuses on detecting an increase in the IQ, while the two-tailed test can detect both an increase or decrease in the IQ.
For more questions related to null hypothesis
https://brainly.com/question/15980493
#SPJ1
Find the explicit formula for the sequence {2,4,8,16,32,...}, and then identify the 18th term of the sequence
Answers
Answer:
2^n
2^18= 262,144
Step-by-step explanation:
Alicia watched a drone take off from a bridge. The height of the drone (in meters above the ground) t minutes
after takeoff is modeled by
h(t) = -3t2 + 12t +96
Alicia wants to know when the drone will land on the ground.
1) Rewrite the function in a different form (factored or vertex) where the answer appears as a number in the
equation
h(t) =
2) How many minutes after takeoff does the drone land on the ground?
minutes
Answers
Answer:
h(t) = -3(t-8)(t+4). and 8 minutes
Step-by-step explanation:
The function can be written as: h(t) = - 3(t² - 4t - 32). As per quadratic equation, after take off, the drone will land on the ground after 8 minutes.
What is a quadratic equation?A quadratic equation is an equation that contains a variable with highest degree of 2.
Given, the height of the drone t minutes after take off is modeled by
h(t) = - 3t² + 12t + 96 = - 3(t² - 4t - 32)
Therefore, the function can be written as: h(t) = - 3(t² - 4t - 32)
Therefore, we can write the equation as:
t² - 4t - 32 = 0
⇒ t²- 8t + 4t - 32 = 0
⇒ t(t - 8) + 4(t - 8) = 0
⇒ (t + 4)(t - 8) = 0
Hence, (t + 4) = 0 and (t - 8) = 0
Therefore, t = -4, 8.
As 't' can't be negative, therefore, t = 8.
Therefore, after take off, the drone will land on the ground after 8 minutes.
Learn more about a quadratic equation here: https://brainly.com/question/11872809
#SPJ2
What is the Next number in this series 7 11 19 35?
Answers
Answer:
67
Step-by-step explanation:
we have a gap between 1st and 2nd terms of 4. a gap between 2nd and 3rd of 8. 16 for next gap. the gap doubles every time.
so we expect gap between 4th and 5th terms to be 2 X 16 = 32.
35 + 32 = 67. that is the next number in the sequence.
a box with a swuare base and open top much have a voume of 32cm^3. find the dimensions of the box that minimise the amount of material used
Answers
The dimensions of the box that minimize the amount of material used are a square base with side length 4√2 cm and a height of 2√2 cm..
To minimize the amount of material used, we need to minimize the surface area of the box.
Let's call the height of the box "h" and the length of each side of the square base "x".
The volume of the box is given by V = x^2 * h = 32 cm^3.
We want to minimize the surface area, which consists of the area of the base (x^2) and the four sides (4xh). So the surface area is given by:
A = x^2 + 4xh
We can solve for h in terms of x using the volume equation:
h = 32 / x^2
Substituting this into the surface area equation, we get:
A = x^2 + 4x(32/x^2)
Simplifying this equation, we get:
A = x^2 + 128/x
To minimize the surface area, we need to find the value of x that makes the derivative of A with respect to x equal to zero:
dA/dx = 2x - 128/x^2 = 0
Solving for x, we get:
x = 4√2 cm
Substituting this value back into the equation for h, we get:
h = 2√2 cm
So the dimensions of the box that minimize the amount of material used are a square base with side length 4√2 cm and a height of 2√2 cm.
To know more about surface area visit:
https://brainly.com/question/29298005
#SPJ11
If the growth rate is 47% what is the growth factor?
Answers
\(\qquad \textit{Amount for Exponential Growth} \\\\ A=P(1 + r)^t\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{initial amount}\\ r=rate\to 47\%\to \frac{47}{100}\dotfill &0.47\\ t=\textit{elapsed time}\\ \end{cases} \\\\\\ A = P(1 + 0.47)^{t} \implies A =P(1.47)^t\hspace{5em}\stackrel{ Growth~Factor }{\text{\LARGE 1.47}}\)
Which of the following is the value of k if one root of the quadratic equation 5m2 2m k 0 is -7 5? One of the roots of equation 5m2 + 2m + k = 0 is-7/5find the value of 'k'.
Answers
If one of the roots of the given quadratic equation is -7/5 then the value of k is -7.
According to the question,Given: - We are having the quadratic equation 5m² + 2m + k = 0 and also one of the roots of the equation an given as -7/5
To find: - The value of K.
Now we find the value of k: -
∵ one root is given to us = -7/5
∴ m = -7/5 is one solution of the quadratic equation
i.e, m = -7/5 will satisfy the above equation
So, we put the value of m and we get,
5 (-7/5)² +2 (-7/5) + k = 0
49/5 - 14/5 + k = 0
∴ 35/5 +k = 0
⇒ 7 + k = 0
⇒ k = -7
To know more about quadratic equations on brainly: brainly.com/question/30098550
#SPJ4
Complete the equation of the line through
(
−
6
,
5
)
(−6,5)left parenthesis, minus, 6, comma, 5, right parenthesis and
(
−
3
,
−
3
)
(−3,−3)left parenthesis, minus, 3, comma, minus, 3, right parenthesis.
Use exact numbers.
Answers
An equation of the line through the points (-6, 5) and (-3, -3) is y = -8x/3 - 11.
What is the point-slope form?Mathematically, the point-slope form of a straight line can be calculated by using this mathematical expression:
y - y₁ = m(x - x₁) or y - y₁ = (y₂ - y₁)/(x₂ - x₁)(x - x₁)
Where:
m represents the slope.x and y are the points.Next, we would determine the linear equation representing the line which passes through the points (-6, 5) and (-3, -3) by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - y₁ = (y₂ - y₁)/(x₂ - x₁)(x - x₁)
y - 5 = (-3 - 5)/(-3 + 6)(x + 6)
y - 5 = -8/3(x + 6)
y - 5 = -8x/3 - 16
y = -8x/3 - 16 + 5
y = -8x/3 - 11
Read more on slope here: brainly.com/question/23086745
#SPJ1
how to find the measure of each acute angle

Answers
Step-by-step explanation:
This is a right triangle which means one of the angles is 90° and since the sum of interior angles in a triangle is equal to 180 then the sum of two other angles must be 90
7x + 6 + 6x - 7 = 90 add like terms
13x - 1 = 90 add 1 to both sides
13x = 91 now divide both sides by 13
x = 7 to find each angle replace x with 7
7x + 6 = 7×7 - 6 = 55° and
6x - 7 = 6×7 - 7 = 35°
The number of coins in a person's collection changes based on buying, selling, and trading coins. A function defined as f(t) = t³ - 6t² + 9t
is modeled by the table, which represents the number of coins in the coin collection t years since the person began collecting coins.
(Picture has the rest of the problem)

Answers
The statements that are true about the function when graphed on a coordinate plane include the following:
C. The relative minimum of the function is (3, 0)
E. When t > 3, the function is increasing.
How to determine the minimum and maximum function?In order to determine the minimum and maximum of this function, we would have to determine the critical points where the derivative of the function is equal to zero or undefined, and then evaluate the function at these critical points and at the endpoints of the interval.
By taking the first derivative of the given function and factorizing, we have:
f(t) = t³ - 6t² + 9t
f'(t) = 3t² - 12t + 9
3t² - 12t + 9 = 0
t² - 4t + 3 = 0
(t - 3)(t - 1) = 0
t = 3 and t = 1
Therefore, the critical points of the function are at t = 1 and t = 3.
By taking the second derivative of the given function and factorizing, we have:
f''(t) = 6t - 12
At point t = 1, we have:
f''(1) = 6(1) - 12 = -6 (it is less than zero).
Therefore, f(t) has a local maximum at t = 1.
At point t = 3, we have:
f''(3) = 18 - 12 = 6 (it is greater than zero).
Therefore, the function f(t) has a local minimum at t = 3.
At t = 4, f''(4) = 24 - 12 = 12
At t = 5, f''(5) = 30 - 12 = 18
In conclusion, the relative minimum of the function is (3, 0) and when t > 3, the function would increase.
Read more on function here: https://brainly.com/question/29230332
#SPJ1
PLS HELP ILL GIVE BRAILSIT
Which of the following is a true statement about the angles in the figure below?

Answers
Answer:
i think its A sorry if im wrong
Step-by-step explanation:
A factory produces 80,000 candies each day. They produce equal quauntities of four flavors cherry lemon orange and strawberry. The candies are mixed together during packaging . What is the probabillity that a randomly selected cany is orange
Answers
Answer: \(\dfrac14\)
Step-by-step explanation:
Given: The factory produces equal quantities of four flavors cherry lemon orange and strawberry.
Let orange candy= cherry = lemon = strawberry = x
Total candies = x + x + x + x= 4x
The probability that a randomly selected candy is orange = \(\dfrac{x}{4x}=\dfrac14\)
Hence, the probability that a randomly selected candy is orange = \(\dfrac14\)
An animal shelter rescues cats and dogs only. Currently the animal shelter has 121 animals. The amount of dogs is 6 more than 4 times the amount of cats. How many cats and dogs are currently in this animal shelter?
Answers
Answer:
In a certain animal shelter, the ratio of the number of dogs to the number of cats is 15 to 7. If 12 additional cats were to be taken in by the shelter, the ratio of the number of dogs to the number of cats would be 15 to 11. How many dogs are in the shelter?
A. 15
B. 25
C. 30
D. 45
E. 60
The probability that X is a 2, 11, or 12 is:
a.) 1/36
b.) 2/36
c.) 3/36
d.) 4/36
Answers
Answer:
The correct answer is c.) 3/36.There are three favorable outcomes (2, 11, and 12) out of a total of 36 possible outcomes (assuming a fair six-sided number cube). Therefore, the probability of X being a 2, 11, or 12 is 3/36, which can be simplified to 1/12.
Step-by-step explanation:
The circumference would , 1 of 2. select choice . for example, a circle with a radius of 3 feet would have a circumference that is about 18 feet. when the radius doubles to 6 feet, the circumference is about , 2 of 2. select choice feet.
Answers
The circumference of the circle with a radius of 6 feet would be approximately 37.7 feet.
The circumference of a circle is the distance around the outer edge of the circle. It is the perimeter of the circle, which is the total length of the boundary that encloses the area of the circle.
The formula for the circumference of a circle is
C = 2πr
Where C is the circumference, r is the radius, and π is approximately 3.14.
If a circle has a radius of 3 feet, the circumference would be
C = 2πr
C = 2π(3)
C ≈ 18.85 feet
When the radius doubles to 6 feet, the circumference would be
C = 2πr
C = 2π(6)
C ≈ 37.7 feet
Learn more about circumference here
brainly.com/question/26605972
#SPJ4
Answer:
double, and 36
Step-by-step explanation:
Mc graw hill
Q...
For altitudes up to 36,000 feet, the relationship between ground temperature and atmospheric
temperature can be described by the formula t = -0.0035a +g, in which t is the atmospheric
temperature in degrees Fahrenheit, a is the altitude, in feet, at which the atmospheric temperature is
measured, and g is the ground temperature in degrees Fahrenheit. Solve the equation for a. If the
atmospheric temperature is -17.4°F and the ground temperature is 40 °F, what is the altitude?
The equation for a is a =
If the atmospheric temperature is -17.4 °F and the ground temperature is 40 °F, then
a= feet.
Answers
Answer:
a=16400 feet
Step-by-step explanation:
t = -0.0035 a +g
-17.40 = -0.0035 a+40
-17.40-40=-0.0035a+40-40
-57.40=-0.0035a
a = -57.40/-0.0035
a=16400 feet
one-sample z test of the assumed 95% lower n mean se mean bound z p 8 105.20 1.77 ? ? ? standard deviation 5 mu 100 vs 7 100. ) fill in the missing values in the output. can the null hypothesis be rejected at the 0.05 level of significance? explain your answer. (b) suppose that the alternative hypothesis had been what is the p-value in this situation? can the null hypothesis be rejected at the 0.05 level of significance? (c) suppose that you were asked to find a 95% two-sided ci on the mean. would the lower confidence bound in the two-sided ci be greater than the one-sided lower confidence bound that you computed in part (a)?
Answers
The null hypothesis can be rejected at the 0.05 or 5 % level of significance according to Decision Rule.
The null hypothesis is a type of hypothesis that explains the population parameter and is used to examine if the provided experimental results are reliable. Depending on whether the population or sample under consideration is viable, this hypothesis is either rejected or not. Or to put it another way, the null hypothesis is a hypothesis that assumes that the sample observations are the product of chance. It is claimed to be a claim made by surveyors who wish to look at the data. The symbol for it is H0.
Given : n = 8
\(\large \bar{X}=105.20 \\\\ \larg\frac{\sigma}{\sqrt{n}}=1.77 \\ \\ \large \alpha=0.05 \large \mu_0=100\)
a ) We want to find the 95% confidence interval for mean
Therefore ,
\(\large (105.20-Z_{0.05}*1.77,105.20+Z_{0.05}*1.77)\\\\\large (105.20-1.64*1.77,105.20+1.64*1.77)\\\\\large (105.20-2.9028,105.20+2.9028)\)
(102.2972,108.1028)
b ) Hypothesis :
\(\large H_0:\mu=100 \\ \\ \large H_1:\mu\neq 100\)
The test statistic under H is given by ,
\(\large Z\rightarrow N(0,1)\\\\ \large Z =\frac{105.20-100}{1.77}\\\\ \large =\frac{5.20}{1.77}\\\\\large =2.9379\)
\(P value \large =P(Z > |Z_{cal}|)\)
=P(Z>2.9379)
=0.001652
Decision Rule : If P value \(< \large \alpha\) then reject at \(\large \alpha\) % level of significance accept otherwise
Here , P value = 0.001652 < \large \alpha = 0.05
Therefore , reject H at 5% level of significance.
Learn more about Null Hypothesis:
https://brainly.com/question/15980493
#SPJ4
Rochelle used these steps to evaluate the power. (â’ 3 4 ) 3 1. Identify the base: â’ 3 4 1. Determine the exponent: 3 3. Write in expanded form: (â’ 3 4 ) (â’ 3 4 ) (â’ 3 4 ) What is the value of the power? Negative StartFraction 9 Over 12 EndFraction Negative StartFraction 27 Over 64 EndFraction StartFraction 9 Over 12 EndFraction StartFraction 27 Over 64 EndFraction.
Answers
The value of power is 27/64.
Given thatRochelle used these steps to evaluate the power.
\( \left (\dfrac{3}{4}\right )^3\)
We have to determineWhat is the value of power?
According to the questionTo determine the value of the power following all the steps given.
Expression; \( \left (\dfrac{3}{4}\right )^3\)
Then,
The value of power is,
\(= \dfrac{3}{4} \times \dfrac{3}{4} \times \dfrac{3}{4}\\ \\ = \dfrac{9}{16} \times \dfrac{3}{4}\\\\ = \dfrac{27}{64}\)
Hence, The value of power is 27/64.
To know more about Powers click the link given below.
https://brainly.com/question/18297177
Answer:
-27/64
Step-by-step explanation:
The coordinates of the midpoint of gh are m(-13/2,-6) and the coordinates of one endpoint are g(-4,1). what is the other endpoint?
Answers
Applying the midpoint formula, the coordinates of the other endpoint are: (-9, -13).
How to Apply the Midpoint Formula?The midpoint formula, which can be used in determining the coordinates of the midpoint between two endpoints is usually expressed as: M[(x1 + x2)/2, (y1 + y2)/2].
Given the following coordinates:
Midpoint of GH --> m(-13/2,-6) = (x, y)
One endpoint ---> G(-4, 1) = (x1, y1)
The other endpoint ---> (x2, y2)
Plug in the values into the formula used in calculating the midpoint:
m(-13/2,-6) = [(-4 + x2)/2, (1 + y2)/2]
Solve for x2
-13/2 = (-4 + x2)/2
-13/2 × 2 = -4 + x2
-13 = -4 + x2
-13 + 4 = x2
-9 = x2
x2 = -9
Solve for y2
-6 = (1 + y2)/2
2(-6) = 1 + y2
-12 = 1 + y2
-12 - 1 = y2
-13 = y2
y2 = -13
Thus, using the midpoint formula, the coordinates of the other endpoint are: (-9, -13).
Learn more about the midpoint formula on:
https://brainly.com/question/13115533
#SPJ1
Solve the following simultaneous equations :
1. x + 2y = 1, 3x - y = 17
Answers
Answer: x= 5 and y= -2
Step-by-step explanation:
(1 point) find the limits, if they exist, or type dne for any which do not exist. lim(x,y)→(0,0)3x24x2 5y2 1) along the x-axis: 2) along the y-axis: 3) along the line y=mx : 4) the limit is:
Answers
The limit as (x, y) approaches (0, 0) along the x-axis is 1.
The limit as (x, y) approaches (0, 0) along the y-axis is 1.
The limit as (x, y) approaches (0, 0) along the line y = mx is also 1.
The overall limit is 1.
To find the limits as (x, y) approaches (0, 0), we substitute the given values into the expression and evaluate the result. Let's examine each case:
Along the x-axis, y = 0, so the expression becomes lim(x)→0 3x^2/(4x^2 + 1). By plugging in x = 0, we get 0/(0 + 1) = 0/1 = 0. Therefore, the limit along the x-axis is 0.
Along the y-axis, x = 0, so the expression becomes lim(y)→0 1/(5y^2 + 1). By plugging in y = 0, we get 1/(0 + 1) = 1/1 = 1. Therefore, the limit along the y-axis is 1.
Along the line y = mx, we substitute y = mx into the expression and simplify. The expression becomes lim(x)→0 3x^2/(4x^2 + 5m^2x^2 + 1). By factoring out x^2 from the denominator, we get lim(x)→0 3x^2/(x^2(4 + 5m^2) + 1). Canceling out x^2, we have 3/(4 + 5m^2 + 1/x^2). As x approaches 0, the term 1/x^2 becomes infinitely large, so the expression simplifies to 3/(4 + 5m^2). Therefore, the limit along the line y = mx is 3/(4 + 5m^2).
Since the limit along the x-axis, y-axis, and y = mx all yield the same value of 1, we can conclude that the overall limit as (x, y) approaches (0, 0) is 1.
Learn more about x-axis here:
https://brainly.com/question/2491015
#SPJ11
Use the figure to the right to find the value of PT. T is the midpoint of PQ.
PT = 4x + 5 and TQ = 8x-7
Answers
Answer:
PT = 17
Step-by-step explanation:
Since T is the midpoint of PQ, then
PT = TQ , substitute values
4x + 5 = 8x - 7 ( subtract 4x from both sides )
5 = 4x - 7 ( add 7 to both sides )
12 = 4x ( divide both sides by 4 )
3 = x
Thus
PT = 4x + 5 = 4(3) + 5 = 12 + 5 = 17
Answer:
17
Step-by-step explanation:
since T is mid point of PQ
PT=TQ
\(4x + 5 = 8x - 7 \\ 5 + 7 = 8x - 4x \\ 12 = 4x \\ x = 12 \div 4 \\ x = 3 \\ \)
so
\(pt = 4x + 5 \\ = 4(3) + 5 \\ = 12 + 5 \\ pt = 17\)